从第一宇宙速度谈起：宇宙有多大？

龚明，中国科学技术大学

摘要：我们用第一宇宙速度估计了宇宙的尺寸，基于此，可以猜测也许整个宇宙可以被当作一个巨大的黑洞。因此，在普通物理力学的教学中，可以利用第一宇宙速度理解黑洞和宇宙尺寸。

学习过一点物理的人都知道第一宇宙速度的概念，它说的是如果朝地球外抛一个物体，当它的速度足够快以后，它将围绕这地球运动，再也回不到地球上了。这个速度可以写成下面的形式\begin{equation}v=\sqrt{GM/R}.\end{equation}这个表达式中，$G$为宇宙常数，$M$为地球的质量，$R$为地球的半径。当然，这个公式存在一个预言，如果考虑的不是地球，而是一个黑洞，任何光都不可能逃脱它的引力，所以黑洞的半径、质量将满足这样的关系\begin{equation}R\le GM/c^2.\end{equation}

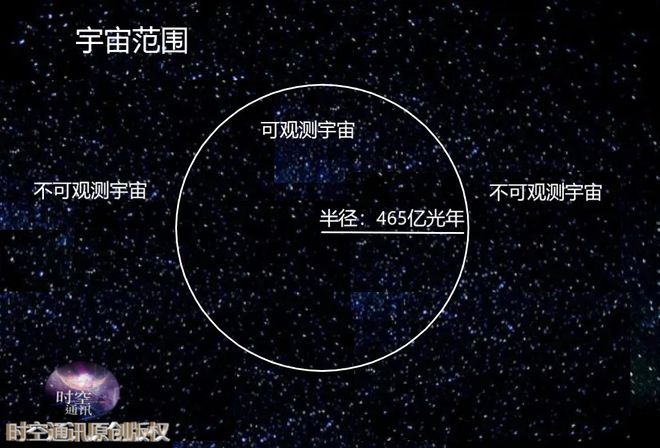
其实，我们还可以用这个公式做另外一个构想，即用它估计我们宇宙的尺寸。假设宇宙的平均密度为$\rho$，质量$M = \rho 4\pi R^3/3$，那么在宇宙以外，任何光线都逃脱不了其吸引，所以宇宙的半径为\begin{equation}  \sqrt{G4\pi R^2/3} = c.\end{equation}通过查具体的数字，得到$G = 6.67\times 10^{-11}$ m$^3$/(kg $\cdot$ s$^2$)，$\rho = 4.7 \times 10^{-28}$ kg/m$^3$, 一光年距离为$9.46\times 10^{15}$米，那么可以估计得到$R = 875$亿光年。这个数字比天文学家认识的465亿光年要大一些（见下图），可能是公式估计出来的问题，或者参数选择的问题（主要是平均密度等）；但是它们在同一个数量级，因此是有意义的。当然，利用这个半径，我们可以估算出宇宙的总的质量\begin{equation}M={c^3\pi \over 6G^{3/2}\pi^{3/2}\rho^{1/2}} = 5.2 \times 10^{52} \text{ kg}.\end{equation} 目前主流天文学家认为的质量，大概在$10^{53}$ kg量级，和这个估计也差不多。我们看到，宇宙的质量，只和三个常数有关：$G$，$c$以及$\rho$，读者也可以通过标度分析获得这些结果。

由此可见，我们只需要用一点点简单的高中知识，就可以估算出整个宇宙的尺寸。我相信高中生也可以明白这个道理。如果这样，我们是不是可以将整个宇宙看作一个黑洞，而我们就在黑洞中呢？这就很好玩了，当然科学家还没有完全证实这一结论。没有想到，物理定律，竟然决定了我们人类的认知边界。当然，这个宇宙的尺寸，应该是我们视觉上（或者可以观测到）的最大尺寸。在这个视觉之外，宇宙可能依旧存在，只是我们看不到。