数学是描述现实世界数量关系和空间形式的知识体系，数学的最本质特征是其客观真理性。被誉为“数学皇帝”的丘成桐教授曾在多个公开场合自豪地宣称：“没有一个学科能像数学一样，对世界的描述经得起时间考验”。

图1 丘成桐教授

布朗运动是物理学中的一个著名现象。1827年，英国植物学家布朗用显微镜观察悬浮在液体中的花粉微粒时，发现微粒总是在做无规则运动。后来人们发现，这是一种广泛存在于自然科学、工程技术和社会科学等领域中的随机现象，如空气污染扩散、陀螺随机游走和股票价格波动等。

但是，数学家们建立的《随机过程》布朗运动理论不仅与爱因斯坦布朗运动理论、牛顿力学和《物理学》实验结果矛盾冲突，而且无法正确描述实际布朗运动现象及规律，为自然科学、工程技术和社会科学提供了错误的理论、方法及工具。

本文指出了数学家们在定义布朗运动时产生的违反同一律“混淆概念”逻辑错误，并给出了解决问题的方法。

一、爱因斯坦对布朗运动的描述

1905年，爱因斯坦首先对布朗运动进行了定量研究。爱因斯坦认为布朗运动是布朗粒子宏观扩散现象的微观表现形式，布朗粒子在宏观扩散过程中，受液体分子的碰撞会在微观尺度下产生不规则运动（图2）。

图2 布朗粒子在微观尺度下的不规则运动

爱因斯坦首先假设“同一布朗粒子在不同时间间隔中的运动相互独立”，若用现代科学语言表述，就是“布朗粒子瞬时速度为白噪声”。

2010年，美国得克萨斯大学李统藏对布朗粒子的瞬时速度进行了实验测量，实验结果表明：布朗粒子的瞬时速度为白噪声（图3），实验验证了爱因斯坦的布朗运动理论假设。

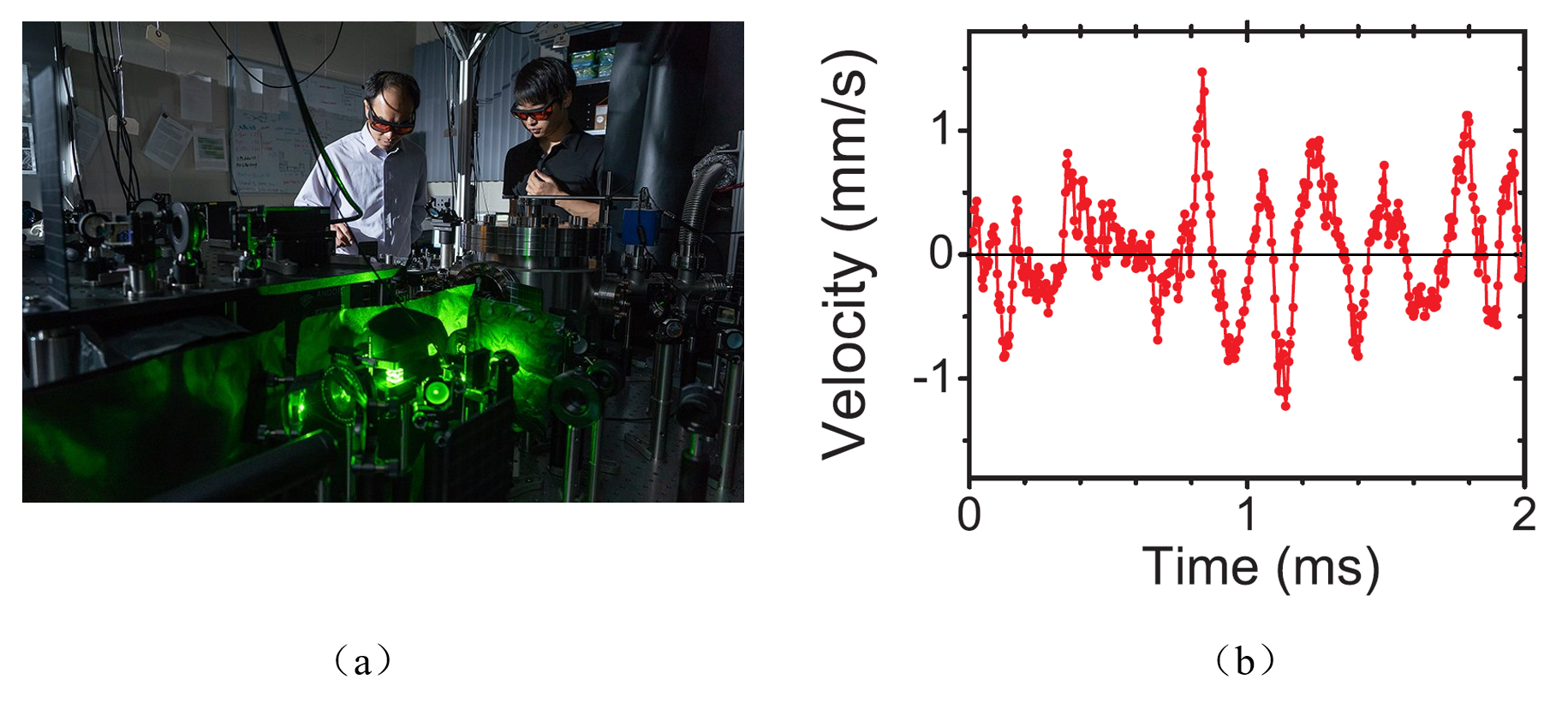
图3 李统藏布朗运动瞬时速度实验及结果

爱因斯坦根据上述布朗运动假设，推导出了描述大量布朗粒子从高浓度区域向低浓度区域转移过程的扩散方程，并求出了扩散方程的解析解：

f(x,t)～N(0，2Dt)

式中f(x,t)为t时刻在位置x处的浓度（单位体积粒子数），D为扩散系数。

上式表明，布朗粒子在扩散过程中的浓度f(x,t)服从（0，2Dt）正态分布，图4为布朗粒子在扩散过程中某一时刻的空间位置及浓度正态分布曲线。

图4 布朗粒子在某一时刻的空间位置及浓度正态分布曲线（面）

1908年，法国物理学家佩兰对布朗运动进行了实验研究，实验结果表明：布朗运动浓度服从爱因斯坦布朗运动扩散方程描述的正态分布。佩兰同时也第一次用实验证明了原子的存在，并于1926年获得了诺贝尔物理学奖。

二、薛定谔对布朗运动的描述

1944年，薛定谔在其著作《生命是什么？》中，对爱因斯坦布朗运动理论进行了更为直观形象的图形描述。

取一个密闭的玻璃容器，再用由微小液滴组成的雾填充容器底部，你会发现雾气的上缘将以固定速率逐渐下沉（图5a）。该速率取决于空气的黏度、液滴的大小及其受到的重力。然而，若在显微镜下观察其中的某个液滴，你会发现它并不是以恒定的速率沉降的，而是在做一种极不规则的运动，即所谓的布朗运动（图5b）。

图5 薛定谔对布朗运动的宏观和微观描述

总之，爱因斯坦和薛定谔均认为：布朗粒子在宏观尺度下做图5a所示的匀速直线运动，在微观尺度下做图5b所示的随机运动。

三、数学家对布朗运动的描述

1913年，美国著名应用数学家、被誉为“控制论之父”的维纳（Wiener）在英国剑桥大学留学期间，在罗素（Russell）的建议下阅读了爱因斯坦1905年发表的布朗运动论文。

维纳发现：爱因斯坦只描述了大量布朗粒子在扩散过程中的浓度分布规律，而没有涉及“一个微粒所走曲线的数学性质”。

为了研究一个布朗粒子所走曲线的数学性质，维纳将爱因斯坦描述大量布朗粒子集体行为的浓度分布规律当作一个布朗粒子个体行为的位移变化规律，给出了如下的布朗运动定义：

X(t)～N(0，σ² t)

式中X(t)为布朗粒子在t时刻的位移，σ² =2D。

维纳根据“布朗运动位移服从正态分布”的定义，推导出了“布朗运动瞬时速度不存在（布朗运动路径处处不可导）”的著名论断，与爱因斯坦的理论假设和李统藏的实验规律完全不符。

根据正态分布的对称性和集中性特征，可仿真出维纳布朗运动定义描述的布朗粒子位移曲线（图6），显然，与图5所示的布朗粒子位移曲线完全不符。

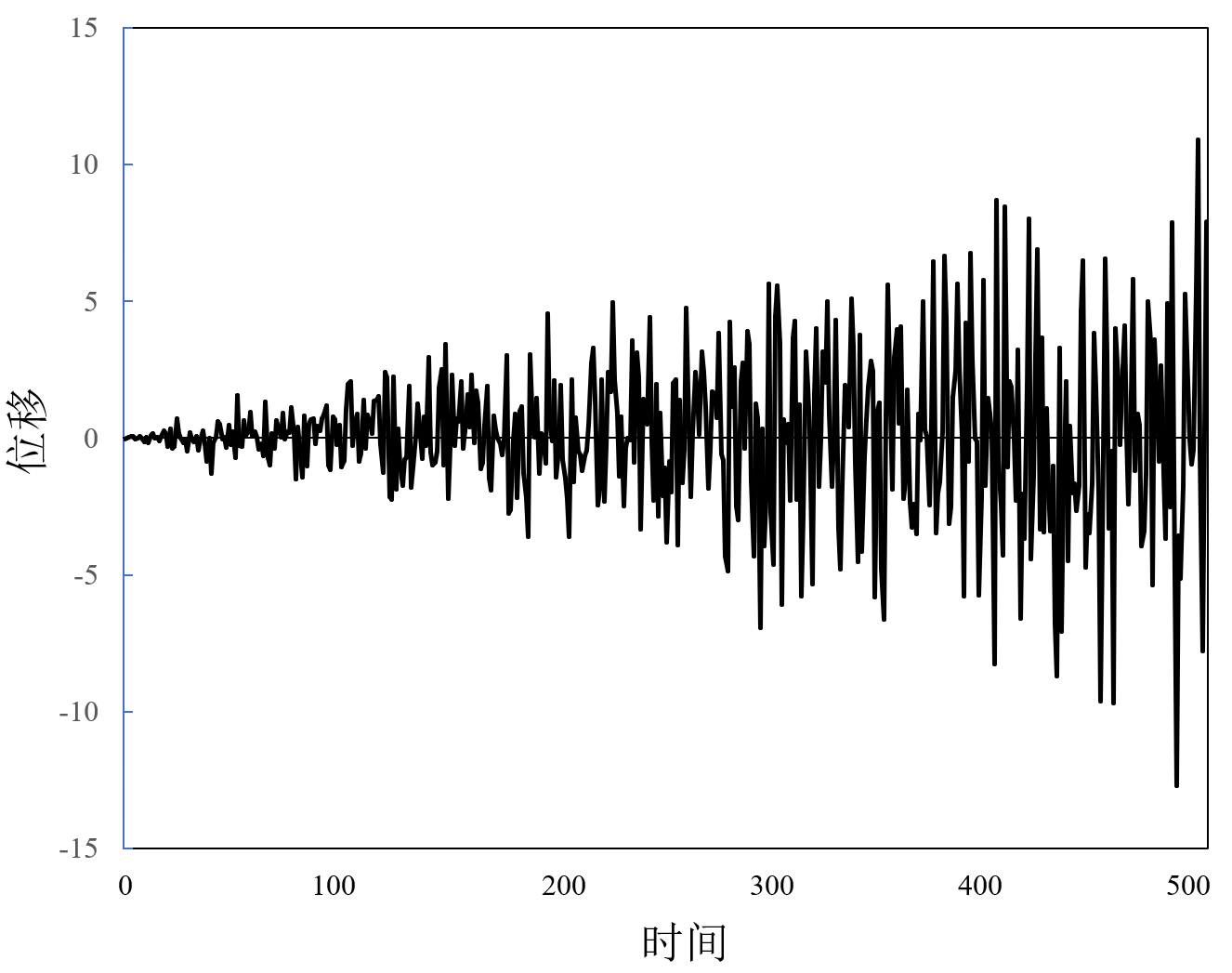
图6 维纳对布朗运动位移的微观和宏观描述

表1为数学家和物理学家对布朗运动的描述对比。

表1 数学家和物理学家对布朗运动的描述

布朗粒子在《物理学》中属宏观粒子，其运动状态受《牛顿力学》的支配。因此，布朗粒子的位移与时间成正比，但是数学家们却有意违反《牛顿力学》，顽固地认定布朗粒子的位移与时间的平方根成正比。

四、原因分析

维纳混淆了物理学中的“浓度”和“位移”基本概念，将描述大量布朗粒子“集体行为”的统计量（浓度）和描述一个布朗粒子“个体行为”的物理量（位移）等同使用，产生了违反同一律的“混淆概念”逻辑错误，就如同用“温度”来描述一个分子的“动能”一样荒谬，导致《随机过程》教科书布朗运动理论的基本假设和逻辑结论均与客观事实不符，无法正确描述布朗运动现象及规律。

另外一个更为搞笑的原因是：研究现实世界随机现象的应用数学家们与现实世界完全脱节，闭门造车，既不去了解自然科学、工程技术和社会科学等领域的理论和实验研究成果，也从不使用实验检验方法来验证数学理论的客观真理性，却一心要为自然科学、工程技术和社会科学提供分析和解决实际问题的数学方法、数学理论及数学工具。

五、解决方法

直接将爱因斯坦的“同一布朗粒子在不同时间间隔中的运动相互独立”理论假设或李统藏的“布朗粒子瞬时速度为白噪声”实验规律作为布朗运动定义，有

式中x(t) 布朗粒子在t时刻的位移， n(t)为白噪声。

因此有

上式描述的布朗粒子位移曲线如图7所示。显然，布朗粒子在扩散过程中的位置变化，在宏观尺度下表现为匀速直线运动，在微观尺度下表现为随机运动，与图5完全一致。

图7 布朗粒子位移曲线（微观和宏观）

六、结论

《随机过程》教科书出现与爱因斯坦布朗运动理论、牛顿力学和李统藏布朗运动实验结果不符的反常问题，预示着《随机过程》教科书即将发生重大范式转换。《随机过程》教科书中原有的错误内容将会被新方法和新理论所取代，这为中国的数学学科进入世界一流水平前列提供了千载难逢的历史性发展机遇。

参考：

[1] 教科书中两种对立冲突的布朗运动理论及实际应用效果

https://blog.sciencenet.cn/blog-3418723-1458326.html

[2] 公理化方法重建随机过程理论（预印本）

https://blog.sciencenet.cn/blog-3418723-1476973.html