THEORY OF OXYGEN TRANSPORT TO TISSUE - PMC

五、微循环中的氧转运模型

本节将综述血液-组织转运的几何概念模型，重点阐述其数学表达式与求解方法。这些模型在特定组织中的应用将在第六节中讨论。

A. 毛细血管-组织氧交换

1. 毛细血管转运的克罗格组织圆柱模型

克罗格（Krogh）提出的“毛细血管与组织间氧转运的组织圆柱模型”[102]，已成为众多理论研究的基础与起点（参见Kreuzer[99]的综述）。该模型也被广泛应用于生理学研究，以估算组织内的氧分布。本节将综述基于“克罗格组织圆柱几何结构”的模型发展历程——尽管克罗格的原始模型基于多项简化假设，且这些假设在后续应用中已逐步放宽，但这类模型通常仍被统称为“克罗格模型”。

克罗格模型的核心假设是：组织可被划分为多个圆柱形单元，每个单元内均有一根沿轴线方向分布的毛细血管，且各单元之间不发生氧交换（图13）。在构建这一几何模型时，克罗格参考了骨骼肌中的毛细血管结构——该组织中肌纤维具有优先排列方向，而毛细血管往往沿肌纤维方向分布。

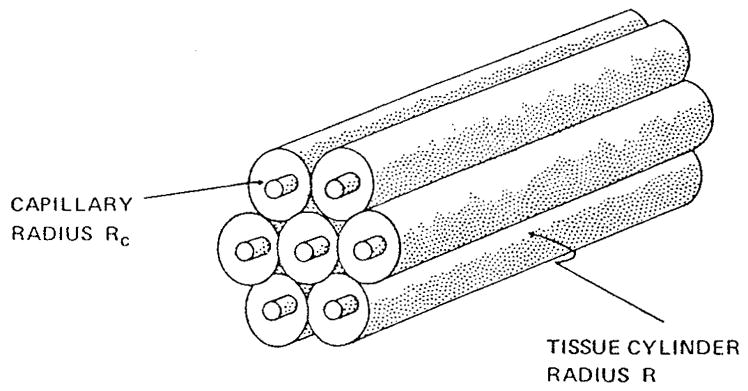
图13.克罗格组织圆柱模型的几何结构

为推导描述组织氧转运的方程，作出以下假设：

1组织圆柱内的氧分压（PO2）分布具有轴对称性。

2组织对氧气的渗透率（即克罗格扩散系数，K = Dtɑt）与空间位置无关（其中Dt为组织中氧气的扩散系数，ɑt为组织中氧气的溶解度系数）。

4组织中的氧气不与载体（如肌肉中的肌红蛋白）结合。

在上述假设下，描述组织内氧转运的方程可表示为：

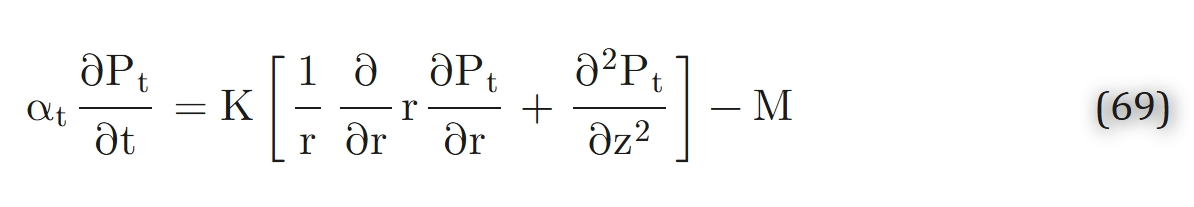
根据“相邻组织单元间不发生氧交换”的假设，组织圆柱外边界处的氧气通量为零，即：

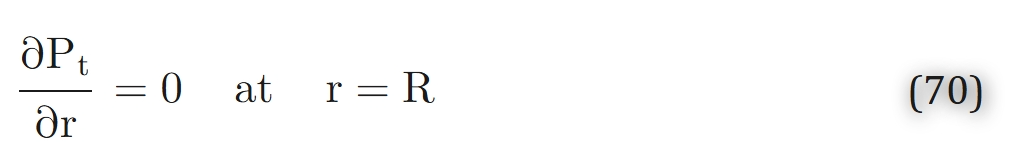
克罗格进一步补充了以下假设：

4稳态条件（此时方程69中的∂Pt/∂项为零）。

5氧气消耗速率恒定（M为常数）。

       6轴向扩散可忽略（∂2Pt/∂z2项数值极小）。

克罗格未考虑毛细血管内的氧转运过程，而是直接给定了毛细血管壁处的氧分压：

（其中Rc为毛细血管的半径，Pw为毛细血管壁处的组织氧分压）

结合边界条件（式70、式71）求解方程69，得到：

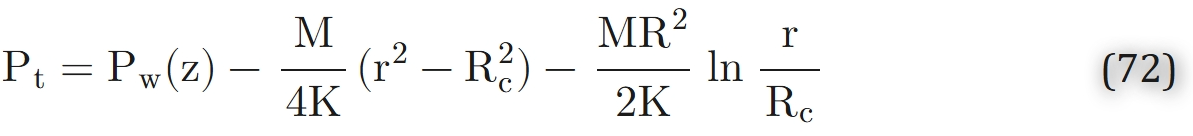
该解由克罗格的同事、数学家厄兰（Erlang）推导得出。式72通过毛细血管半径、组织圆柱半径及组织渗透率，描述了组织氧分压的径向分布。借助该式，可计算出组织氧分压的最小值——该最小值出现在组织圆柱的外边缘（即r=R处）。

前文已讨论过毛细血管内的氧转运过程。由于血液具有颗粒性（由红细胞和血浆组成），描述毛细血管转运时有两种选择：其一，通过明确考虑红细胞和血浆，对转运过程进行详细描述[3,19,35]；其二，引入毛细血管横截面上的平均变量，并分析这些变量沿毛细血管轴向的变化。前者与组织转运模型结合后，会形成复杂的非稳态问题，目前尚未得到充分研究；后者的思路可概述如下：

假设毛细血管横截面内“充分混合”，则通过任意横截面的氧气体积通量可表示为[94]：

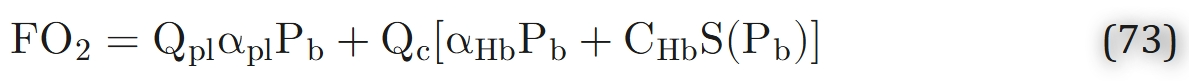
其中Pb为毛细血管内氧分压，Q{pl}为血浆的体积流量，Qc为红细胞的体积流量，αpl为血浆中氧气的溶解度系数，αHb为红细胞内血红蛋白溶液中氧气的溶解度系数，C_Hb为血红蛋白溶液的氧结合能力，S(Pb)为氧合血红蛋白饱和度，是毛细血管内氧分压Pb的函数。

式73中，第一项代表血浆中游离氧气的对流通量，第二项代表红细胞内游离氧气的对流通量，第三项代表与血红蛋白结合的氧气的通量。若将红细胞和血浆的体积流量表示为Qc = QHD、Qpl=Q(1-HD)（其中HD为毛细血管排出血细胞比容，Q为血液的总体积流量），则可将通过毛细血管横截面的氧气通量改写为游离氧与结合氧的通量之和：

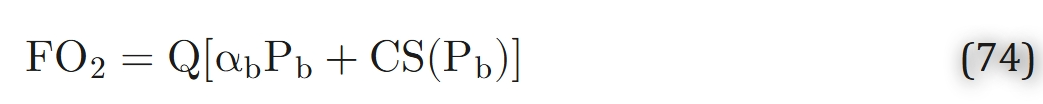
（其中αb = (l − HD)αpl + HDαHb为血液中氧气的溶解度系数，C = HDCHb为血液的氧结合能力）

毛细血管内氧气的质量平衡方程可表示为：

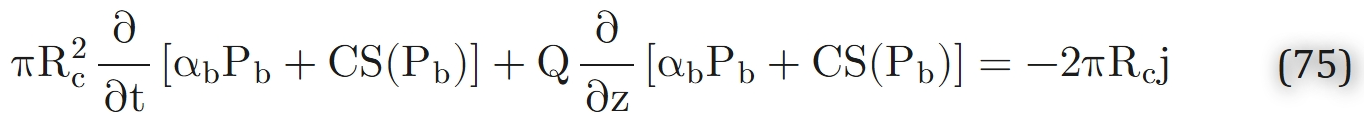
（其中j为毛细血管-组织界面处的氧气通量）

推导式75时隐含以下假设：

- 血红蛋白与氧气的化学反应瞬时完成，即反应速率远快于式75所考虑过程的速率。

在毛细血管-组织界面处，氧气通量连续，即：

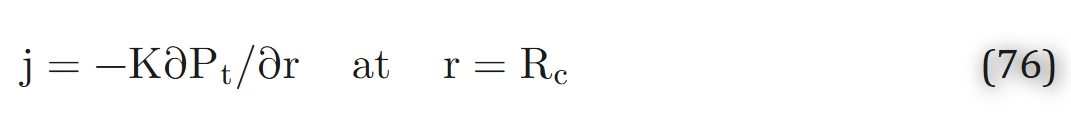
同时，毛细血管内氧分压与组织氧分压的关系可通过传质系数表示为：

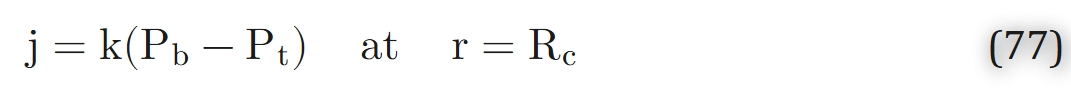
（其中k为毛细血管-组织界面处的氧气传质系数）

此外，毛细血管入口处的氧分压为已知条件：

（其中Pa为毛细血管动脉端入口处的氧分压，z=0为毛细血管动脉端起点）

传质系数由该领域早期研究者引入[12,25]，最初被理解为毛细血管膜的渗透率。若k为无穷大，则毛细血管水平的氧转运无阻力；目前认为，k的有限值主要源于红细胞内部及血浆中的氧转运阻力[35,62]。

有部分学者采用不同方法处理该问题，例如假设毛细血管内氧气为自由扩散且传质系数无穷大（如Reneau等人[145,146]）。但结合近年来对毛细血管内转运的研究可知，本文提出的方法更为合理。

在稳态、无轴向扩散且组织氧气消耗速率恒定的条件下，毛细血管-组织间的氧气通量j为常数（与z无关），即j = π(R2 − Rc2)M——这意味着在轴向位置z处从毛细血管扩散出的氧气，恰好被z处的组织切片消耗。由此可对式75进行积分：

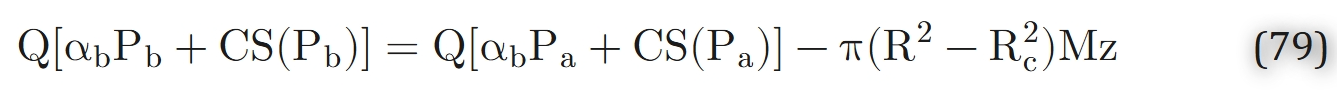
（其中下标“a”代表毛细血管动脉端的参数）

若忽略游离氧浓度（与结合氧浓度相比可忽略不计），且采用希尔方程（式4）描述氧合血红蛋白解离曲线，则可通过式79表示氧分压沿毛细血管的分布：

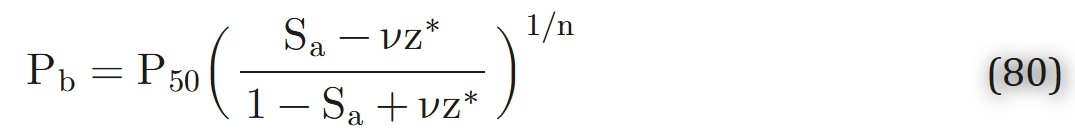
（其中v =π(R2 −Rc2)ML/CQ，z* =z/L，P50为氧合血红蛋白饱和度为50%时的氧分压，Sa为毛细血管动脉端的氧合血红蛋白饱和度，L为毛细血管的长度，n为希尔系数）

毛细血管-血液界面处的组织氧分压可由式77求得：

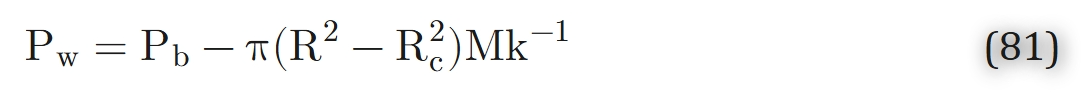 在上述简化假设（1-7）下，式72、式80与式81共同构成了该氧转运问题的完整解。

多年来，研究者们投入大量精力，围绕不同生理条件下假设（1-7）的有效性、放宽这些假设的方法，以及通过数值与解析手段求解克罗格几何结构下完整氧转运问题展开研究。Reneau及其同事（Reneau等人[145,146]、Knisely等人[96]）采用有限差分法对该问题进行了系统的数值研究，其中考虑了组织中的轴向扩散，假设氧气消耗遵循零级化学动力学，并通过求解方程描述缺氧区域的形成过程，同时也分析了非稳态扩散的情况。

当考虑组织中的轴向扩散时，需补充组织氧分压在z=0和z=L平面处的边界条件，通常设定为无通量边界条件。研究者不仅考虑了毛细血管内氧气的径向扩散，还纳入了轴向扩散；但研究表明，在大多数情况下，毛细血管轴向扩散的影响可忽略，径向扩散的影响也较小。

图14展示了他们的部分计算结果，呈现了当氧结合能力C（图中以N表示）降低时，组织中缺氧区域的形成过程。需注意的是，这些情况需求解组织中的非线性扩散方程，无法通过解析解（式72、式79）描述。

克罗格组织圆柱模型几何结构的一个典型特征是“致命角”（lethal corner）——即位于毛细血管静脉端平面、组织圆柱外边缘处的区域。该区域的组织氧分压最低，因此当氧气供应不足时，缺氧和无氧状态会首先在此处出现。后续将看到，其他毛细血管-组织转运几何模型并未提出“致命角”的概念。

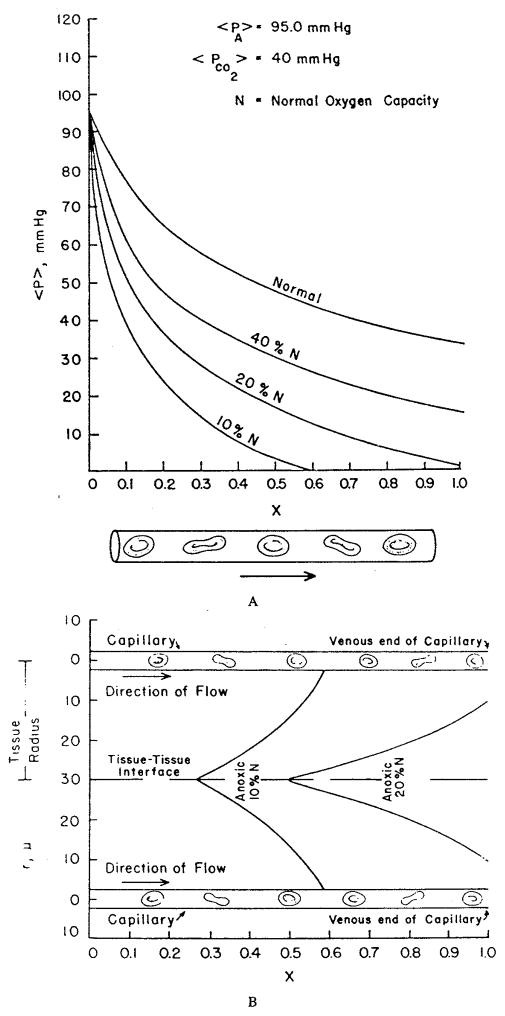
图14.（a）根据克罗格模型得到的毛细血管内氧分压（PO₂）分布，展示了血细胞比容（氧结合能力）降低的影响。横坐标上的数值为毛细血管总长度的占比。图中红细胞仅为示意，血液被视为均质血红蛋白溶液；（b）血细胞比容降低导致的平行同向毛细血管间组织缺氧区域。（来源：Knisely, M. H.、Reneau, D. D., Jr. 与 Bruley, D. F.，《血管学》，第29卷，S1期，1969年。已获转载许可。）

若对微分方程（69）中的空间坐标进行适当的无量纲化处理（令r^* = r/R，z^* = z/L），则z^*方向的二阶导数项将乘以参数\varepsilon^2 = (R/L)^2。在诸多重要情况中（尤其是骨骼肌和心肌组织），该参数数值较小，因此问题在数学上可大幅简化。最高阶导数项前带有小参数的问题，属于一类广泛的奇异摄动问题（当\varepsilon = 0时，方程的阶数发生变化，故称为“奇异”）。这类问题可通过匹配渐近展开法求解[107]。

Salathe等人[150]采用该方法，针对氧气消耗速率恒定的稳态问题，得到了直至\varepsilon^2阶的三项渐近展开解，其中忽略了毛细血管内的氧转运阻力，并通过解析方法估算了轴向扩散项的贡献。匹配渐近展开法还被应用于血管闭塞后缺氧区域形成的问题研究中（Salathe与Wang[153]）。

Hyman等人[81]通过数值方法求解了一个略有不同的“周期性毛细血管闭塞”问题。但该研究额外纳入了一种影响因素：缺氧状态下组织产生乳酸，而乳酸可通过氧化作用被清除，此过程会消耗氧气（即氧债）。研究中，将乳酸浓度换算为清除这些乳酸所需的氧气浓度。图15展示了缺血恢复过程中，“致命角”处的氧分压计算值，以及组织圆柱内空间平均氧分压的计算值。此外，研究者还得到了反应性充血情况下的求解结果（Hyman与Artigue[82]）。

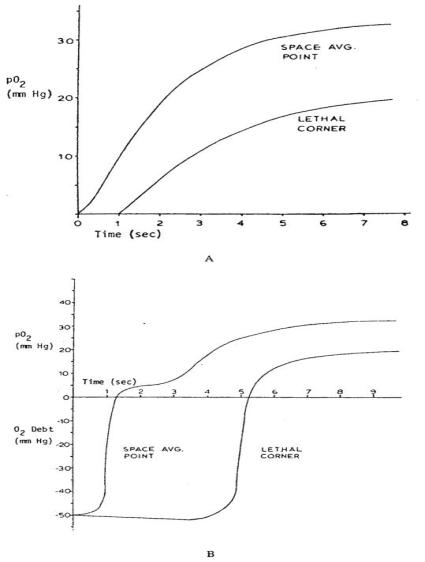
图15.用于计算血管闭塞后恢复过程的克罗格模型：（a）无 oxygen debt（氧债）情况；（b）闭塞2分钟后存在氧债的情况。（来源：Hyman, W. A.、Grounds, D. J. 与 Newell, P. H., Jr.，《微血管研究》，第9卷，第49页，1975年。已获转载许可。）

弗莱彻（Fletcher）[38]以通用形式构建了该问题的模型，除轴向扩散和毛细血管壁的有限阻力外，模型还纳入了血红蛋白-氧气（Hb-O₂）反应的动力学效应。他为毛细血管区域建立了两个方程，分别对应游离氧和结合氧，随后通过数值方法求解该问题，并对多数参数的敏感性进行了分析。结果表明，非平衡动力学对氧分布的影响仅为轻微程度。

2. 非克罗格几何结构的毛细血管转运模型

从某种意义上说，克罗格组织圆柱模型具有通用性，已被应用于多种组织的研究，但需根据组织特性调整参数，如组织圆柱半径、毛细血管半径、毛细血管血流量、氧气消耗速率及组织对氧气的渗透率等。另一方面，大多数非克罗格几何结构模型均反映了特定组织的形态学特征。因此，在第六节（综述不同组织中转运过程的理论结果）讨论这些特定模型会更为合理。本节将聚焦适用于多数组织的通用模型发展历程及核心特征。

通过推广克罗格模型的方程（式69、式75），可勾勒出任意毛细血管几何结构下数学问题的构建框架。考虑由非均质组织环绕的任意毛细血管网络，若组织中不存在氧载体，则氧转运方程可表示为：

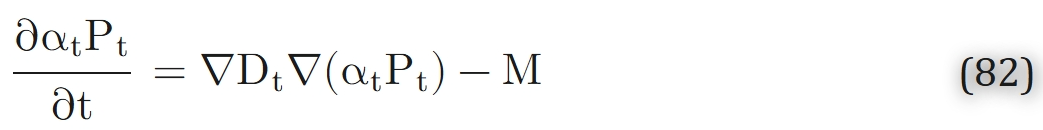
通常情况下，氧气扩散为三维过程；而在克罗格模型（式69）中，由于问题具有轴对称性，仅考虑径向和轴向扩散。此外，式（82）中允许扩散系数、溶解度系数及氧气消耗速率作为空间坐标的函数，即转运特性具有非均匀性。这种非均匀性可能存在于细胞层面（例如，生化组成不同的肌纤维、大脑中的神经胶质细胞与神经元），也可能存在于更大尺度上（例如，缺血损伤组织与正常组织相邻的区域）。在各向异性组织（如骨骼肌和心肌）中，扩散也可能具有各向异性[71]，因此不同方向的扩散系数需以张量形式表示。

若假设毛细血管横截面内“充分混合”，则式（75）仍可适用，唯一差异在于需将轴向坐标z替换为沿毛细血管的曲线坐标（记为q）：

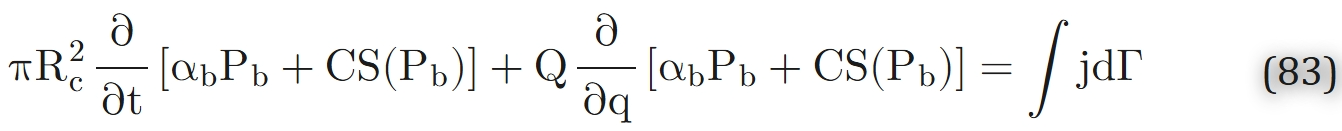 （其中Rc为毛细血管半径，αb为血液中氧气溶解度系数，Pb为毛细血管内氧分压，C为血液氧结合能力，S(Pb)为氧合血红蛋白饱和度，Q为血液体积流量，j为毛细血管-组织界面处氧气通量，Г为“q=常数”平面与毛细血管表面的交线，积分沿该交线进行）

在毛细血管-组织界面处，满足以下条件：

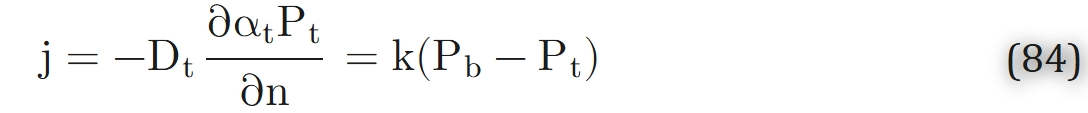 （其中∂/∂n为沿毛细血管表面外法向的偏导数，k为毛细血管-组织界面处氧气传质系数）

组织区域的边界还需补充边界条件，这些条件取决于对“该区域与周围组织关系”的假设。多数情况下，将该区域视为“微循环单位”，即组织主体可划分为多个呈周期性或对称性排列的此类单位。这种几何结构意味着单位边界处需满足周期性边界条件或无通量边界条件。若组织存在可与外界环境进行氧交换的外表面，则需为该表面设定不同的边界条件，例如指定表面氧分压或表面传质系数。

文献中提出的非克罗格几何结构组织模型，均为上述通用框架的特殊情况。克罗格组织圆柱可视为最简单的微循环单位，尽管圆柱形无法完全填充空间。泰斯（Thews）[177]及赫德森与卡特（Hudson and Cater）[77]提出了可填充空间的六边形圆柱模型，波佩尔（Popel）[134]提出了方形圆柱模型，这些模型与克罗格模型的差异较小。

格鲁内瓦尔德与索瓦（Grunewald and Sowa）[56]提出了“微循环单位（MCU）”的概念，每个单位由四根毛细血管供血，毛细血管上设有动脉入口和静脉出口（图16）。这些出入口的不同排列方式可形成不同的微循环单位，示例见图17。通过对毛细血管末端进行系统性“螺旋式”位移，可构建出256种微循环单位，其中21种具有独特结构。当所有毛细血管为同向流动时（微循环单位1），该问题本质上可简化为方形克罗格组织圆柱模型。在其他情况下，单位内的毛细血管间可能发生扩散交换（分流）。该模型为单位的侧面设定无通量边界条件，为上下表面设定周期性边界条件。由于组织区域为平行六面体（长方体），可采用有限差分法对该问题进行数值求解。该模型已应用于骨骼肌[56]、心脏[57]的研究，经改进后还应用于大脑研究[93]。

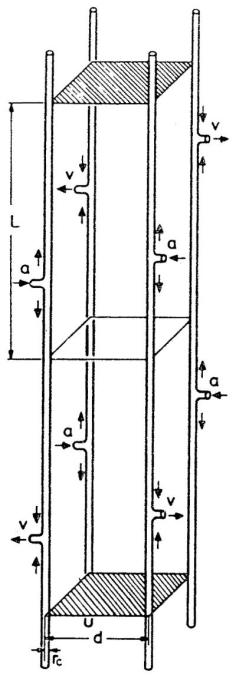
图16.微循环单位（MCU）的结构特征

微循环单位（MCU）由一段长度为2L的组织片段和4根平行分布的毛细血管组成，其中L等于毛细血管的长度，即动脉入口（a）与静脉出口（v）之间的距离。两根毛细血管之间的最短距离为d；rc为毛细血管半径。短箭头表示毛细血管内的血流方向。组织片段的上表面和下表面用斜线标出。（来源：Grunewald, W. A. 与 Sowa, W.，《生理学、生物化学与药理学评论》，第77卷，第149页，1977年。已获转载许可。）

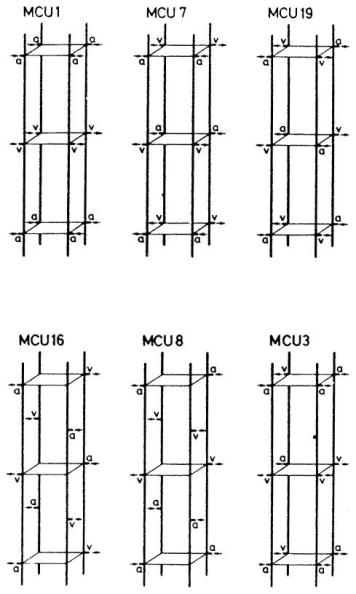
图17.六种微循环单位（MCU）的结构特征

- 微循环单位1（MCU 1）：毛细血管血流方向一致（克罗格毛细血管结构）；

- 微循环单位7（MCU 7）：毛细血管血流部分同向、部分逆向；

- 微循环单位19（MCU 19）：毛细血管血流完全逆向；

- 微循环单位16（MCU 16）：动脉入口（及静脉出口）呈螺旋状排列，彼此错开L/2距离（螺旋结构）；

- 微循环单位3（MCU 3）与微循环单位8（MCU 8）：毛细血管末端排列无特定几何规律（非对称毛细血管结构）。

其中，a代表动脉入口，v代表静脉出口。（来源：Grunewald, W. A. 与 Sowa, W.，《生理学、生物化学与药理学评论》，第77卷，第149页，1977年。已获转载许可。）

波佩尔（Popel）[134,138,140]对克罗格模型进行了拓展，考虑了“由任意数量平行毛细血管贯穿的平行六面体组织”——每根毛细血管可被赋予不同的流速、氧结合能力及入口氧分压（PO₂）。该模型忽略轴向扩散，仅考虑垂直于毛细血管轴线平面内的扩散，因此属于准二维问题。

在文献[134]中，研究人员采用格林函数法（Green function method），通过解析方式表达了组织内的氧分压分布，随后将问题简化为求解“描述毛细血管内氧分压沿轴向变化的非线性常微分方程”。该解法被用于相邻毛细血管间氧气扩散分流的系统性研究[138,140]。

在另一项研究中[141]，研究人员根据特定概率分布，随机设定毛细血管特性（红细胞通量、入口氧分压），通过蒙特卡洛模拟（Monte Carlo simulation）分析氧分压分布的统计特性，并得到了有限差分数值解。具体而言，研究人员先计算大量随机选取的微循环单位的氧分压分布，再对这些结果进行集合平均。埃尔斯沃思等人（Ellsworth et al.）[31]将该模型应用于横纹肌研究。

文献[168]同样探讨了毛细血管氧交换的随机性——研究假设毛细血管各段的氧合血红蛋白饱和度呈线性分布，尝试推导毛细血管网络中氧合血红蛋白饱和度概率分布的解析表达式。

上述研究均局限于平行毛细血管几何结构。然而，即便在作为模型原型的骨骼肌和心肌中，毛细血管的几何排列也可能存在显著差异；而在大脑等组织中，毛细血管更是呈现出随机的几何分布模式。梅茨格（Metzger）[120]提出了“晶格型微循环单位”（图18），其中毛细血管形成“同向与逆向血流混合”的立方网状结构；他还考虑了二维晶格结构（毛细血管构成的矩形网格）。该模型被应用于大脑内的氧转运研究。

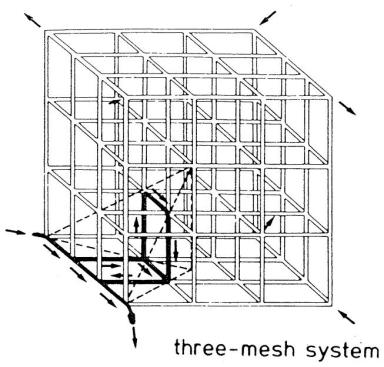
图18.三维立方毛细血管网状模型

该模型由一个包含3×3×3根毛细血管的组织立方体构成。输入点与输出点分别位于立方体的对角处。根据对称性，仅需使用图中所示的四面体进行数值模拟即可。（来源：Metzger, H.，《数学生物科学》，第30卷，第31页，1976年。已获转载许可。）

这些模型即便针对特定组织构建，也能反映不同组织中毛细血管网络的通用结构排布。更具组织特异性的几何模型（如适用于大脑、皮肤的模型）将在第六节中讨论。

3. 氧转运的连续介质描述

组织转运过程中的异质性存在于不同空间尺度：（1）细胞内尺度；（2）细胞尺度，例如氧气消耗速率不同的相邻细胞，或一对逆向流动的毛细血管；（3）毛细血管网络尺度，例如血流速率一高一低的相邻毛细血管网络；（4）器官宏观尺度。针对这些尺度的转运描述，需采用不同的数学方法。

Salathe[152]提出，要理解氧气向特定器官的整体供应方式，无需对毛细血管间的精细尺度变化进行描述。因此，他通过“体积平均法”平滑精细尺度的变化，进而研究组织中氧气的大尺度转运问题。模型假设局部区域的毛细血管呈平行分布（尽管不同区域的毛细血管方向可能不同），且精细尺度梯度远小于大尺度梯度。研究引入单一氧气浓度c，同时表征组织和毛细血管中的氧气水平。通过推导，得到了关于浓度c的单一偏微分方程：

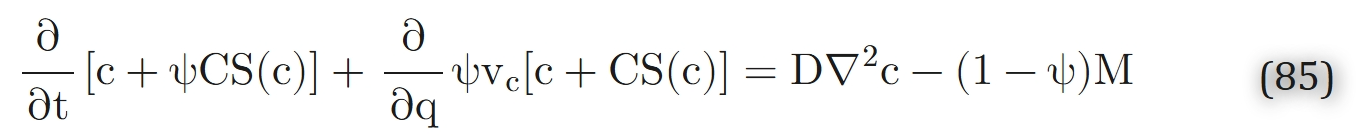
式中，ψ为毛细血管占据的体积分数，vc为毛细血管内血流速度，q为沿毛细血管的坐标，C为血液氧结合能力，S(c)为氧合血红蛋白饱和度（与氧气浓度c相关），D为氧气扩散系数，M为组织单位体积氧气消耗速率。

借助式（85），无需计算单根毛细血管周围的氧气分布，即可求解不同组织区域间的扩散相互作用问题。图19展示了“由入口血液浓度不同的毛细血管供血的两个相邻组织区域”之间的相互作用。

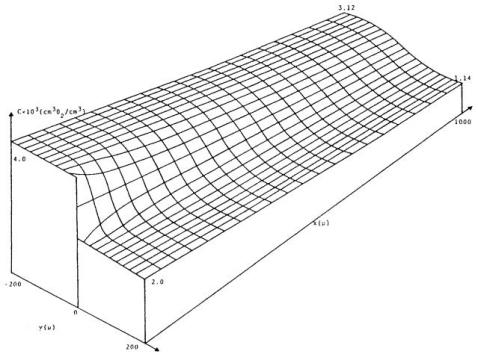
图19.由两组初始浓度不同的相邻毛细血管灌注形成的毛细血管-组织氧浓度分布。x轴沿毛细血管方向；距离单位为微米。（来源：Salathe, E. P.，《数学生物科学》，第58卷，第171页，1982年。已获转载许可。）

该模型的局限性之一在于其可预测氧浓度变化的最小尺度。在推导过程中，并未严格规定浓度平均所采用的体积大小；但显然，该体积至少应与毛细血管间的特征距离相当。因此，对于小于毛细血管间距尺度的浓度变化，该模型的预测结果并不可靠。

 B. 毛细血管前（动脉端）与毛细血管后（静脉端）转运模型

过去20年间的实验发现表明，小动脉与周围组织之间存在大量氧气交换[133]，这促使科研人员构建了“氧气从小动脉向组织、从组织向小静脉转运”的数学模型。此外，关于成对小动脉与小静脉之间是否存在氧气逆向交换（逆流交换）的问题，也引发了广泛讨论（Harris[60]）。这种小动脉与小静脉成对分布的解剖结构十分常见（Wiedeman[189]）。

波佩尔与格罗斯（Popel and Gross）[135]首次构建了小动脉-组织转运模型。在该模型及此后构建的其他类似模型中，均假设小动脉横截面内“充分混合”，且不考虑小动脉内部的氧转运阻力；因此，描述小动脉管腔氧转运的方程与毛细血管相同，即式（83）。小动脉管壁的氧转运由一个类似于式（82）的扩散方程控制——由于小动脉管壁没有独立的氧气供应来源，其氧气需通过管腔扩散获得。

对于包含实质细胞和毛细血管的血管外区域，模型采用唯象学方法构建（即不考虑组织结构的具体细节）。稳态条件下，该区域的氧转运可用以下线性方程描述：

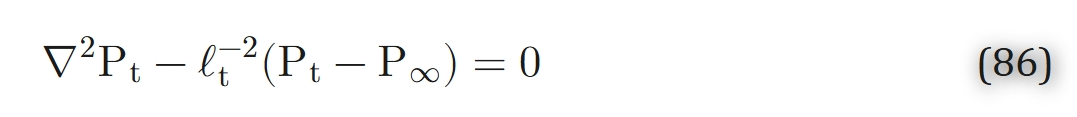
式中，P∞为远离小动脉处的背景氧分压，ℓt 为名为“渗透深度”的唯象学参数，用于表征氧气源或氧气汇产生的扰动可渗透的距离。

该方程被应用于小动脉-组织交换问题（Popel and Gross[135]、Pittman[133]、Kuo and Pittman[104]），以及成对小动脉与小静脉间的逆流交换问题（Sharan and Popel[166]）。在后者的研究中，通过数值方法求解式（86），随后将问题简化为求解“描述两根血管内氧分压沿轴向分布的耦合非线性常微分方程组”。与实验数据的对比显示，该理论显著低估了小动脉的氧气通量[104]。

为解决唯象学模型的不确定性，研究人员构建了一个新模型，该模型明确纳入了毛细血管网络几何结构与血流动力学的相关信息（Weerappuli and Popel[185]）。对小动脉外区域氧转运的描述基于式（85）。该问题的数值解表明，小动脉与其周围的毛细血管及组织之间存在显著的扩散相互作用。图20展示了小动脉周围的氧分压等高线（毛细血管血流方向从左至右）。由于这种扩散相互作用，小动脉下游会形成一个延伸范围较广的“高氧分压尾流区”。波佩尔等人（Popel et al.）[142]将该模型应用于近期获取的实验数据分析[104]。结果与此前模型的分析结论在定性上一致[135]；该模型预测的组织氧渗透率K = Dt\alphat（Dt为组织氧扩散系数，\alphat为组织氧溶解度系数）比当前公认值高一个数量级。目前，尚未深入探究这一预测结果对氧转运其他方面的全面影响。

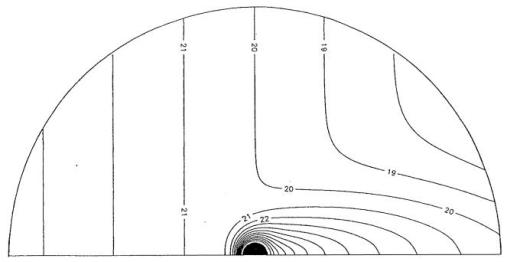
图20. 氧分压（PO₂）在小动脉周围分布的等高线图

在血液-血管壁界面处，氧分压P = P{\text{管腔}} = 31.6托（torr）。小动脉管腔以黑色显示。为清晰起见，未展示无血管的管壁部分。毛细血管血流方向为从左至右。由于小动脉与周围组织间的扩散交换，在小动脉后方形成了一个氧分压升高的“尾流区”。（来源：Weerappuli, D. P.V. 与 Popel, A. S.，《生物力学工程杂志》，第111卷，第24页，1989年。已获转载许可。）

西科姆与许（Secomb and Hsu）[160]对“由一段小动脉和若干独立毛细血管组成的小型网络”的氧分布进行了计算。研究采用格林函数法（Green’s function method），将该问题简化为求解一个积分微分方程。但该方法仅限于组织氧气消耗速率恒定的情况，无法应用于缺氧区域形成的场景。

C. 氧转运的房室模型

截至目前讨论的所有模型，均关注氧气浓度的空间变化——无论是毛细血管内红细胞间血浆间隙的浓度变化，还是小动脉周围组织中的浓度变化。因此，这类模型通常被称为分布模型（distributed model）。另一方面，有一类模型忽略浓度的空间变化，被称为房室模型（compartmental model）：这类模型研究不同“房室”（compartment，即特定区域）之间的物质交换，且每个房室仅用一个浓度值表征。这种划分与系统规模无关：房室既可以是细胞内的区域，也可以代表整个器官。

从数学角度看，分布模型由包含“坐标导数”和“时间导数”（针对非稳态问题）的微分方程描述；而房室模型可能仅包含时间导数。因此，房室模型可通过常微分方程或代数方程描述。

比达尼与弗卢默费尔特（Bidani and Flumerfelt）[11]、希尔等人（Hill et al.）[65]以及萨拉特等人（Salathe et al.）[151]构建了详细的房室模型，这些模型考虑了氧气在红细胞、血浆、组织液和细胞内液等房室中与其他物质的化学相互作用。在更大尺度上，还有研究构建了涉及动静脉扩散分流的房室模型（Piiper et al. [131]）。

此外，还有一类器官循环房室模型：除一个或多个组织紫外，这类模型将“串联的血管群”也视为房室（Roth and Wade [147]）。图21展示了相应的血管与组织排布示意图。较大的小动脉和小静脉通过结缔组织房室进行氧气交换，其他所有血管则与组织房室进行氧气交换。研究为每个房室（血管房室和组织房室）构建了氧气质量平衡方程。对于稳态问题，该过程最终可转化为一个关于“各房室平均氧分压”的非线性代数方程组。下文将结合骨骼肌的研究背景，讨论该模型的预测结果。另有一个拓展版房室模型被应用于大脑氧转运分析（Sharan et al. [167]）。

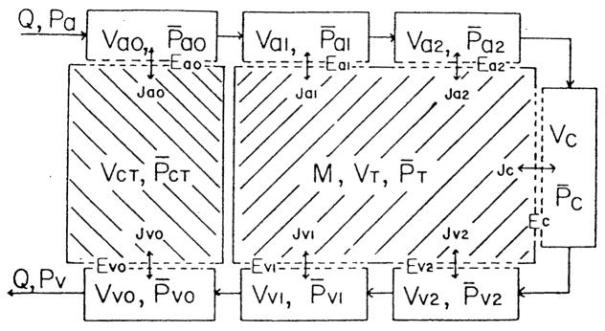
图21.肌肉的房室模型：组织与所有血管结构间存在气体扩散交换，且气体沿循环系统进行对流转运

小动脉（a0、a1、a2）和小静脉（v0、v1、v2）根据血管直径被划分为三个房室；Q代表流经各血管房室（包括毛细血管房室C）的血流量。模型包含两个组织房室：一个代表较大小动脉与小静脉平行段之间的结缔组织（CT），另一个代表肌肉组织（T），其中M为代谢速率。Js代表跨房室边界的通量，通量大小由空间平均分压（P）和扩散传导率（E）决定。（来源：Roth, A. C. 与 Wade, K.，《微血管研究》，第32卷，第64页，1986年。已获转载许可。）

此前仅考虑毛细血管房室内氧交换的模型，已被整合到一个更全面的模型中，该模型包含了血流动力学与调控机制（Granger与Shepherd[48]、Granger与Granger[49]）。

D. 氧转运的最优性

在此有必要提及从“氧转运最优化”角度阐释毛细血管-组织系统结构合理性的相关研究。Wilson[192]构建了一个与克罗格模型类似的模型，差异在于：该模型要求组织圆柱外表面的“总通量”（而非局部通量）为零，且额外要求外表面的氧气浓度保持恒定。随后，他通过“体积平均熵产最小化”的条件确定了毛细血管密度——组织中氧气扩散导致的局部熵产与氧气浓度梯度的平方成正比。Kamiya等人[87]构建了一个模型，将组织单元设为球形（而非圆柱形），并通过“成本函数最小化”的条件确定了全身的毛细血管数量。在这两项研究中，计算得出的毛细血管密度均与实验值基本吻合。Khanin与Bukharov[89,90]基于“功率最小化原理”分析了全身的氧平衡。