引用本文

王立夫, 成昊昱, 孔芝, 郭戈. 多层Snapback网络化数据采样系统能控性. 自动化学报, 2025, 51(9): 2027−2036 doi: 10.16383/j.aas.c250090

Wang Li-Fu, Cheng Hao-Yu, Kong Zhi, Guo Ge. Controllability of multilayer Snapback networked sampled-data systems. Acta Automatica Sinica, 2025, 51(9): 2027−2036 doi: 10.16383/j.aas.c250090

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c250090

关键词

网络能控性，数据采样系统，多层网络，层间耦合

摘要

针对具有Snapback层间耦合框架的多层网络化数据采样系统的状态能控性展开研究. 首先, 构建出多层Snapback网络化数据采样系统的数学模型, 并推导出通用三层Snapback网络化数据采样系统能控性的充要条件, 揭示层内网络拓扑结构、节点动力学、外部控制输入、数据采样及层间耦合框架等因素对系统能控性的影响. 针对层内耦合矩阵为可对角化矩阵的基本Snapback网络化数据采样系统, 进一步简化其能控性条件, 并将其结论进行推广. 然后, 考虑由简单Snapback结构叠加而成的复合Snapback多层网络, 给出网络化数据采样系统能控性的充分条件. 最后, 通过例子验证了所给出的结论.

文章导读

现实世界的许多系统都可以用复杂网络进行描述, 例如, 在人际关系网络中, 可以将每个人作为节点, 两个人之间的关系作为连边. 类似的还有计算机网络、电力网络、社会关系网络等. 复杂网络研究的主要目的是让人们更好地了解网络结构和功能, 进而控制复杂网络的行为使其为人类服务. 在对网络系统实施控制之前, 首先需判定其是否具有完全能控性, 完全能控性是实现系统有效控制的前提. 因此, 网络系统的能控性逐渐成为复杂网络系统研究的热点问题.

人们对能控性最早的认识来源于线性系统理论[1]. 自Kalman首次提出线性时不变系统的能控性定义以来, 过去几十年间, 学者们提出众多能控性判据. 近年来, 随着系统朝着网络化的方向发展, 人们发现这些能控性判据很难直接应用于大规模的复杂网络之中, 因此很多学者相继开展针对大规模复杂网络的能控性的研究[2]. Ding等[3]提出一种基于最小成本最大流的目标能控性算法, 用于在复杂网络中实现最大(最小)覆盖节点的目标能控性, 并通过仿真验证了其有效性. Klickstein等[4]研究发现在保证能控性的前提下, 控制强度与驱动节点和目标节点之间的最大距离呈指数关系. Zhang等[5]提出一种基于空间图神经网络的判断网络能控性鲁棒性的方法, 并验证了其优越的泛化能力和预测性能. Wang等[6]提出一种基于驱动网络的输入设计方法, 定义冗余不可达强连通分量和间歇性不可达强连通分量结构, 并给出最小输入节点数及其配置方案, 以实现大规模复杂网络的结构能控性.

在实际复杂网络系统中, 通常存在多种网络结构与时间尺度相互耦合的现象. 针对这一情况, 研究者更倾向于采用多层网络模型来描述复杂系统. 多层网络的每一层具有与其他层不同的结构模式, 并且层与层之间可以存在多样的交互方式. 这种层与层之间的交互方式, 增加了网络的复杂性, 也为判定网络的能控性带来新的挑战. 当多层网络中的节点都是一维节点时, Chen等[7]通过张量代数和多项式控制理论, 研究超图网络的能控性, 并提出一种类Kalman秩条件的网络能控性判据. Song等[8]提出一种名为MFTP的算法, 能够通过提供最少的外界控制输入使得整个网络是目标能控的. 当多层网络中的节点都是高维节点时, 目前的研究相对较少. Wu等[9]研究层间耦合模式分别为驱动响应模式和相互依赖模式的多层网络, 分别给出系统能控的一些充分或必要条件, 并揭示不同的层间耦合模式对网络系统能控性的影响. Jiang等[10]研究多层网络整体的能控性和构成多层网络的单层网络能控性之间的关系, 发现合适的层间耦合框架可以使得原本不能控的单层网络变得能控. Wang等[11]研究由高维线性时不变动态系统构成的多层复杂网络的目标能控性, 分析层间耦合对其目标能控性的影响, 并给出目标能控性的充要条件及在特定网络结构下的充分条件.

多层网络中, 比较典型的层间耦合结构为Snapback结构, 这种结构的多层网络为多层Snapback网络, 是由一条骨干链和若干条反馈回路组成的. 骨干链表示相邻两层节点之间的级联关系, 反馈回路表示网络中较低层的一些节点可能直接与较高层的节点进行交互. Snapback网络在交通网络、产业网络、生态网络等领域有非常广阔的应用前景[12−14], 并且该网络模型一定程度上与生态系统中经典级联模型和生态位模型具有相似的特征[15−16]. 在经典的控制理论中, 反馈回路对于系统的稳定性和能控性也起到非常重要的作用. 将反馈回路结构引入网络的层间耦合中, 会对网络的能控性带来什么影响, 是本文研究的一个主要问题.

目前, 许多控制系统依托计算机技术实现. 由于计算机系统识别的是数字离散信号, 故需要对系统信号进行数据采样操作. 但在控制通道和传输通道进行数据采样会对网络系统的能控性产生影响[17−23]. Lu等[21]在状态完全解耦的条件下, 提出无需求解Kalman矩阵的图论判据. Yang等[22]研究单层网络化数据采样系统的能控性问题, 揭示单层网络拓扑、节点动力学、内耦合和采样方式对系统能控性的影响, 并提供较低计算复杂度的能控性判据. 同时, Yang等[23]还分别在节点同质和异质的情况下, 针对多层网络化数据采样系统的能控性条件进行研究. 相比之下, 本文所研究的网络拓扑存在多层Snapback结构并且引入层间耦合机制, 使得系统能控性的判定面临新的挑战. 另外, 数据采样过程中存在的多速率采样、时间延迟、信号不稳定等因素将对整个网络系统的能控性带来哪些影响, 都是值得研究的问题.

基于此, 本文研究层间耦合为Snapback框架的多层网络化数据采样系统的状态能控性问题. 主要贡献为以下三个方面: 1)给出通用的三层Snapback网络化数据采样系统能控性的充分必要条件, 揭示层内网络拓扑结构、节点动力学、外部控制输入、数据采样及层间耦合框架等因素对能控性的影响. 2)研究当层内耦合矩阵为可对角化矩阵时的基本三层Snapback网络化数据采样系统的能控性, 进一步简化其能控性判据, 并且将结论推广至M

层的情况. 此外, 得到一些关于三层Snapback网络化数据采样系统能控性的必要条件, 可以直观地快速地识别出不能控的网络. 3)考虑更一般情况, 由简单Snapback结构叠加而成的复合Snapback多层网络, 给出网络化数据采样系统的能控性的充分条件, 表明该系统的能控性可以由构成它的因子网络来表征.

本文的其余部分组织如下. 第1节介绍一些理解本文所需的基础知识. 第2节构建本文的研究对象——多层Snapback网络化数据采样系统的数学模型. 第3节针对多层Snapback网络化数据采样系统的能控性进行研究, 给出一些充分/必要条件及说明例子. 最后, 第4节对全文进行总结并提出未来研究的方向.

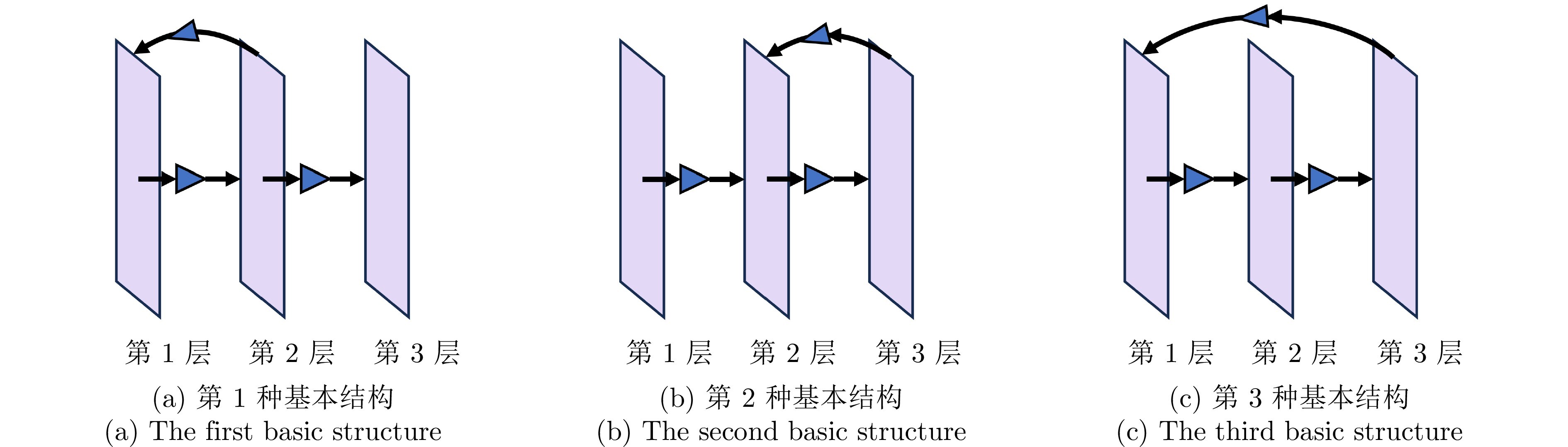
图1  基本三层Snapback网络化数据采样系统

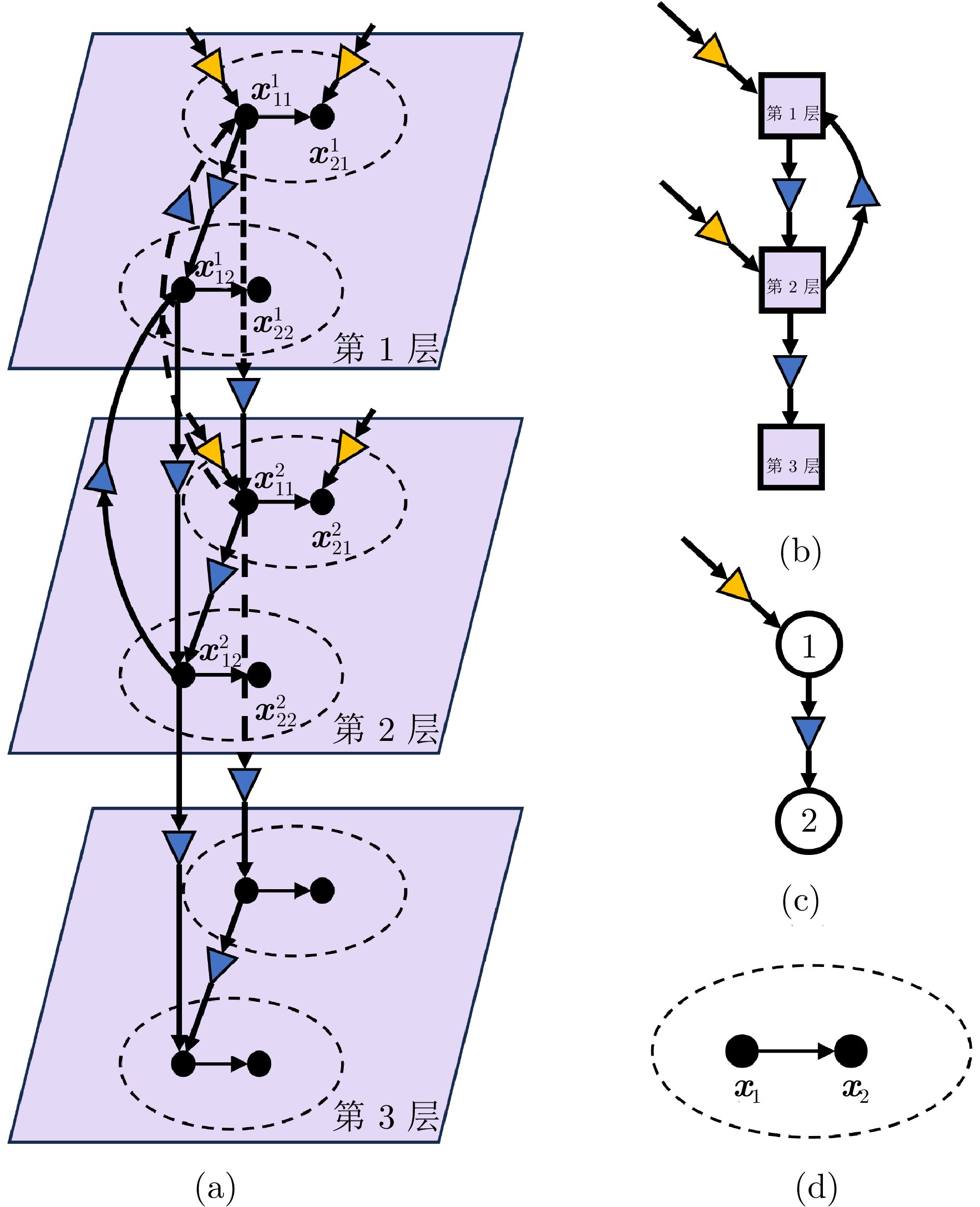
图2  三层Snapback网络化数据采样系统实例(黄色和蓝色的三角形分别表示外界输入的控制采样和系统内部的传输采样) ((a) 整个网络化数据采样系统; (b) 层间耦合拓扑结构; (c) 层内耦合拓扑结构; (d) 单个节点系统)

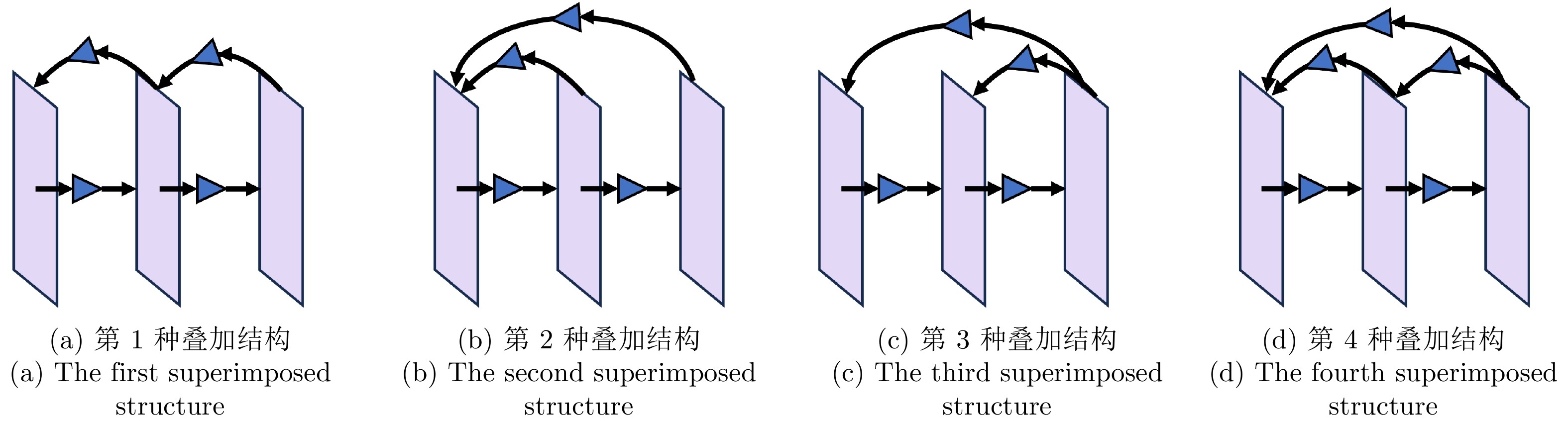
图3  叠加三层Snapback网络化数据采样系统

本文研究具有Snapback层间耦合框架的多层网络化数据采样系统的状态能控性问题. 得到通用三层Snapback网络化数据采样系统能控性的充分必要条件. 并且进一步得到层内耦合矩阵为可对角化矩阵的基本三层Snapback网络化数据采样系统能控性的充分/必要条件, 进一步简化其能控性的判定, 并将其推广至M

层的情况. 此外, 本文还进一步给出由基本三层 Snapback网络化数据采样系统组合而成的叠加三层复合Snapback 网络化数据采样系统能控性的条件. 本文考虑的Snapback网络化数据采样系统是控制通道与传输通道采用相同采样周期的单速率采样系统. 对于多速率采样, 或存在时延与丢包等非理想因素的情况, 其对能控性的影响将是未来研究的一个重要方向.

作者简介

王立夫

东北大学秦皇岛分校控制工程学院副教授. 主要研究方向为复杂网络, 同步控制, 能控性, 交通网络. E-mail: wlfkz@neuq.edu.cn

成昊昱

东北大学秦皇岛分校控制工程学院硕士研究生. 主要研究方向为复杂网络的能控性. E-mail: 2272237@stu.neu.edu.cn

孔芝

东北大学秦皇岛分校控制工程学院副教授. 主要研究方向为知识发现, 决策分析, 智能优化算法, 复杂网络. E-mail: kongz@neuq.edu.cn

郭戈

东北大学教授. 主要研究方向为智能交通系统, 交通大数据分析, 人工智能应用, 信息物理系统. 本文通信作者. E-mail: guoge@qhd.neu.edu.cn