引用本文

丁炜超, 孙立烨, 罗飞, 顾春华, 董文波. 面向复杂可行域约束多目标优化问题的双种群协同进化算法. 自动化学报, 2025, 51(9): 2037−2057 doi: 10.16383/j.aas.c250023

Ding Wei-Chao, Sun Li-Ye, Luo Fei, Gu Chun-Hua, Dong Wen-Bo. Two-population co-evolutionary algorithm for constrained multi-objective optimization problems in complex feasible domains. Acta Automatica Sinica, 2025, 51(9): 2037−2057 doi: 10.16383/j.aas.c250023

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c250023

关键词

约束多目标优化，复杂可行域，协同进化，粒子群优化，向量群引导

摘要

约束多目标优化问题主要考虑如何在复杂约束条件下同时优化多个相互冲突的目标, 其广泛存在于工程实践中. 解决多目标优化问题的关键在于约束满足和目标优化之间的平衡. 然而, 当问题具有复杂可行域时, 现有算法往往存在选择压力大小的矛盾: 若算法的选择压力较大, 种群容易陷入局部最优; 若算法的选择压力较小, 种群则难以搜索到完整的约束前沿. 针对此, 提出一种双种群协同进化约束多目标优化算法. 所提算法采用双种群协同进化框架, 引入粒子群和向量群以实现种群间的信息共享和优势互补. 其中粒子群使用带有辅助档案的粒子群优化器, 通过粒子间的相互学习实现快速收敛, 而辅助档案则借助逃逸机制帮助粒子群跳出局部最优. 同时, 设计一种新的ε-约束技术, 动态调整约束松弛因子, 使种群在进化初期注重不可行解的遗传信息, 跨越不可行区域. 向量群使用不考虑约束的参考向量法引导种群进化, 使种群均匀分布于前沿面, 有效维护了种群的多样性. 在当前基准测试集和真实世界73个问题上的实验结果表明, 所提出的算法超越对比算法, 能够在保持种群多样性的同时快速收敛到约束前沿.

文章导读

约束多目标优化问题(Constrained multi-objective optimization problem, CMOP)指除需要平衡多个相互冲突的目标问题外, 还需服从一组或多组约束条件的一类优化问题. 受真实世界各种条件的限制, 在工程实践中广泛存在着CMOP. 例如车辆调度[1−2]、背包问题[3]、最优产品选择[4] 和工艺工程问题[5−6] 等.

进化算法是一类具有高鲁棒性和广泛适应性的元启发式方法, 在求解CMOP时表现出巨大的潜力[7]. 区别于无约束多目标优化问题, 进化算法求解CMOP时一方面要考虑约束满足和目标优化之间的平衡, 另一方面要在确保约束满足的情况下, 维护种群的多样性和收敛性. 为解决以上挑战, 研究者们提出多种针对约束问题的多目标进化算法(Constrained multi-objective evolutionary algorithm, CMOEA), 根据约束处理方法的不同大致分为三类: 约束主导法(Constrained dominance principle, CDP)[8]、惩罚函数法[9]、ε-约束技术[10]. 其选择规则为: 当所选个体为一个可行解和一个不可行解时, 可行解总优于不可行解; 当两个体均为可行解时, 通过非支配排序确认二者支配关系; 当两个体均为不可行解时, 通过约束违反(Constraint violation, CV)值大小确认优先关系. 由于其原理简单、易于实现, CDP在CMOEA中得到广泛应用, 例如APSEA[11]、C-TBCEA[12]和DSPCMDE[13]. 惩罚函数法向每个目标函数添加约束违反, 将约束优化问题转变为无约束优化问题处理. 在此过程中, 惩罚因子是以参数形式被引入的, 所以未提高原问题维度, 同时也降低了约束处理的难度. 为适应不同类型的约束多目标优化问题, 一些前沿算法例如PF-ICMOA[14]和ICMOEA/D[15]设计惩罚系数的更新机制, 使算法能够根据种群收敛情况调整约束条件的优先级. ε-约束技术最早由Takahama和Sakai[16]提出, 旨在通过阈值ε动态调整算法的选择压力, 从而使算法能够跳出局部可行域. 在该技术中, CV值小于ε值的解被视为可行解. 因此, 该技术能够保留一些不可行解, 从而利用这些不可行解的信息引导进化. ε值的设置对算法性能影响较大, 文献[17−19]提出不同的阈值更新方法, 拓展了ε-约束技术的设计思路.

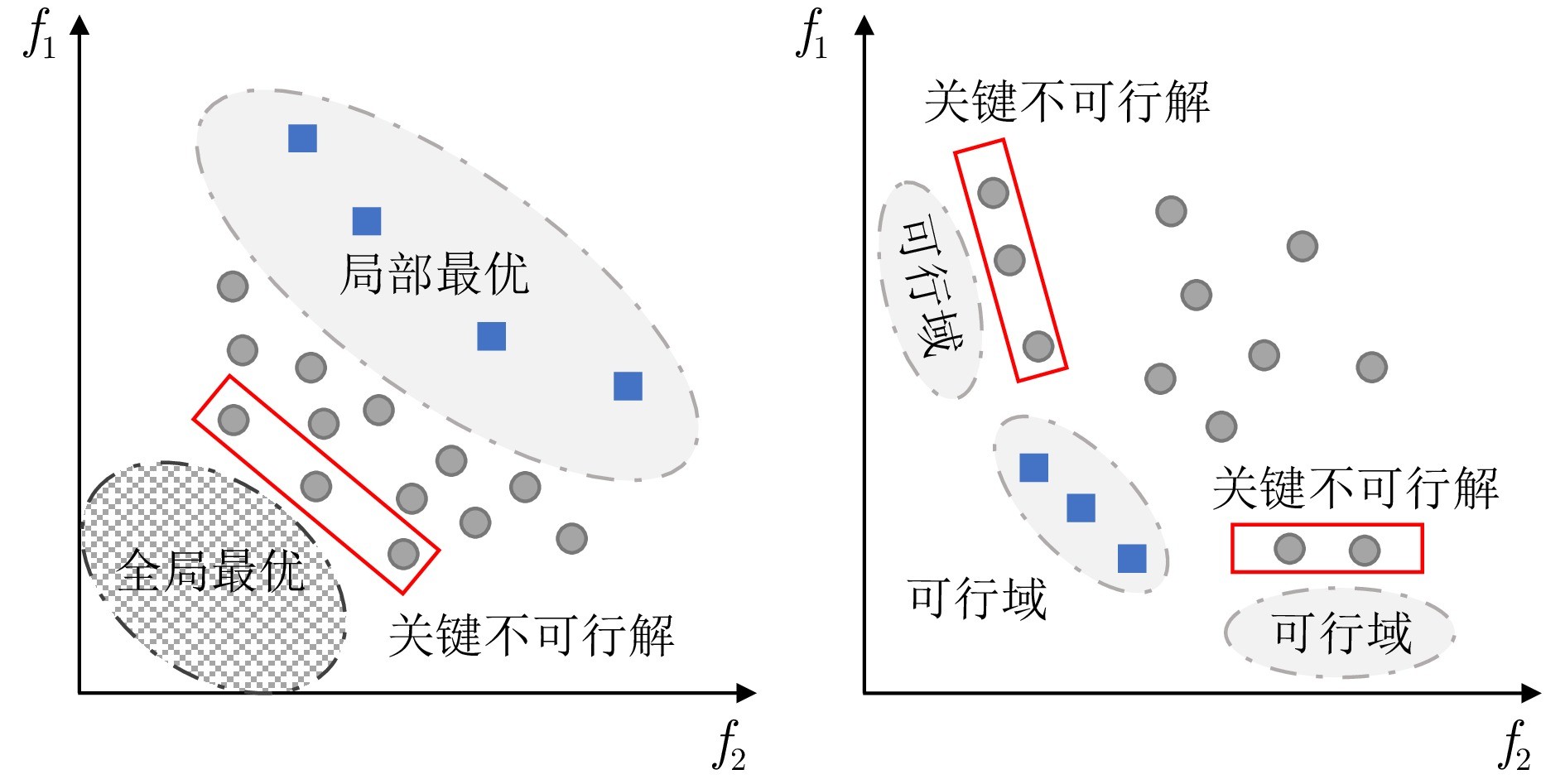
上述的两种约束处理技术(CDP和惩罚函数法), 能够在部分约束形状均匀、分布有明显规律的测试问题上展现出优越性. 然而当可行域较复杂, 例如可行域具有狭窄、离散、互不连通等特殊性质时, 使用这两种技术的算法往往难以搜索到全局最优可行前沿. 这主要归因于二者的选择压力无法自适应调整, 从而难以应对具有复杂不可行域问题. 选择压力是进化算法中用于控制种群进化速度和方向的一种机制. 它决定算法在搜索空间中探索(Exploration)和利用(Exploitation)的平衡. 高选择压力倾向于促进种群的快速收敛, 但可能导致过早收敛从而陷入局部最优; 而低选择压力则有利于维持种群的多样性, 但可能减缓收敛速度. 因此, 在设计进化算法时, 合理地调整选择压力是至关重要的. 尤其在处理复杂约束多目标优化问题时, 需要在保证解可行性和多样性的同时, 快速收敛到约束前沿. 现存ε-约束技术虽然能够动态调整选择压力, 但是均未能将约束违反阈值的自适应机制与问题特性结合, 导致算法的鲁棒性和泛化性较差.

综上所述, 在处理复杂约束时, 若选择压力较大, 算法能够较好地处理连续可行域问题, 但是在解决离散可行域问题或可行域间跨度较大的问题时种群容易陷入局部最优. 若选择压力较小, 算法能够较好地处理离散可行域问题, 但是在解决连续可行域问题时收敛速度过慢导致种群可行率不高. 因此使用单一种群的约束处理机制难以合理调整约束和目标的选择压力. 此外, 基于对复杂约束问题的大量实验观测[20−24]认识到, 在进化过程中保持种群的多样性和逃逸机制的设定对于种群跳出局部最优至关重要. 针对解决复杂可行域问题时算法选择压力大小的矛盾, 我们考虑采用双种群框架. 双种群协同进化框架中两个种群可以有不同的选择压力和进化动态, 这使得算法能同时进行全局搜索和局部搜索; 进化过程中两个种群将周期性地进行个体交换, 算法可控制交换的频率和交换的选择性, 从而平衡整个种群的选择压力. 针对种群的多样性需求, 考虑通过动态生成参考向量来引导种群搜索, 确保种群在目标空间中均匀分布. 参考向量作为目标空间中的引导线, 为种群提供搜索的方向, 使得种群中的个体能够更加均匀地覆盖整个帕累托前沿. 这种方法不仅能够保持种群的多样性, 避免算法过早收敛到局部最优解, 而且能够增强算法对复杂可行域的适应能力. 我们考虑使用粒子群算法的粒子间学习来设计本算法的逃逸机制. 粒子间的相互学习为算法提供一种有效的逃逸机制设计框架, 使算法在面对复杂可行域问题时, 能够更加灵活地调整搜索策略.

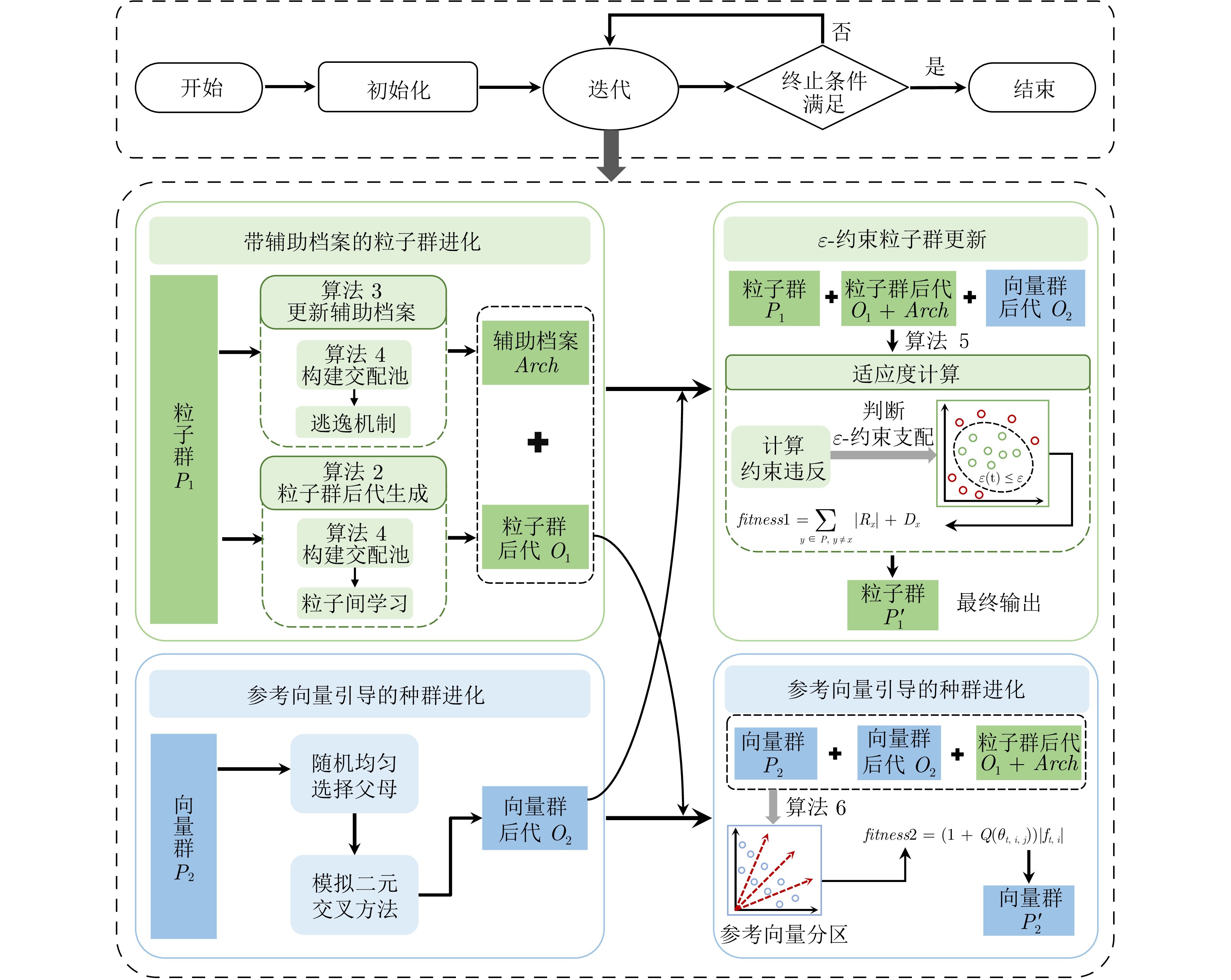
基于上述考虑, 本文所提出的双种群协同进化约束多目标优化算法(Two-population co-evolutionary constrained multi-objective optimization algorithm, TCCMOA)采用双种群协同进化作为算法框架, 粒子群和向量群共享后代以实现两个种群间的优势互补. 其中粒子群同时考虑约束满足和目标优化, 使用带辅助档案的粒子群优化器以实现逃逸机制, 并提出一种新的ε-约束技术来动态调节选择压力. 向量群不考虑约束, 采用参考向量法引导种群进化, 旨在使种群能够在目标空间中均匀分布, 增加种群多样性. 在实验部分使用主流约束多目标测试函数集对TCCMOA进行综合评估, 实验结果验证了所提算法可以有效应对上文出现的问题.

具体而言, 本研究贡献如下:

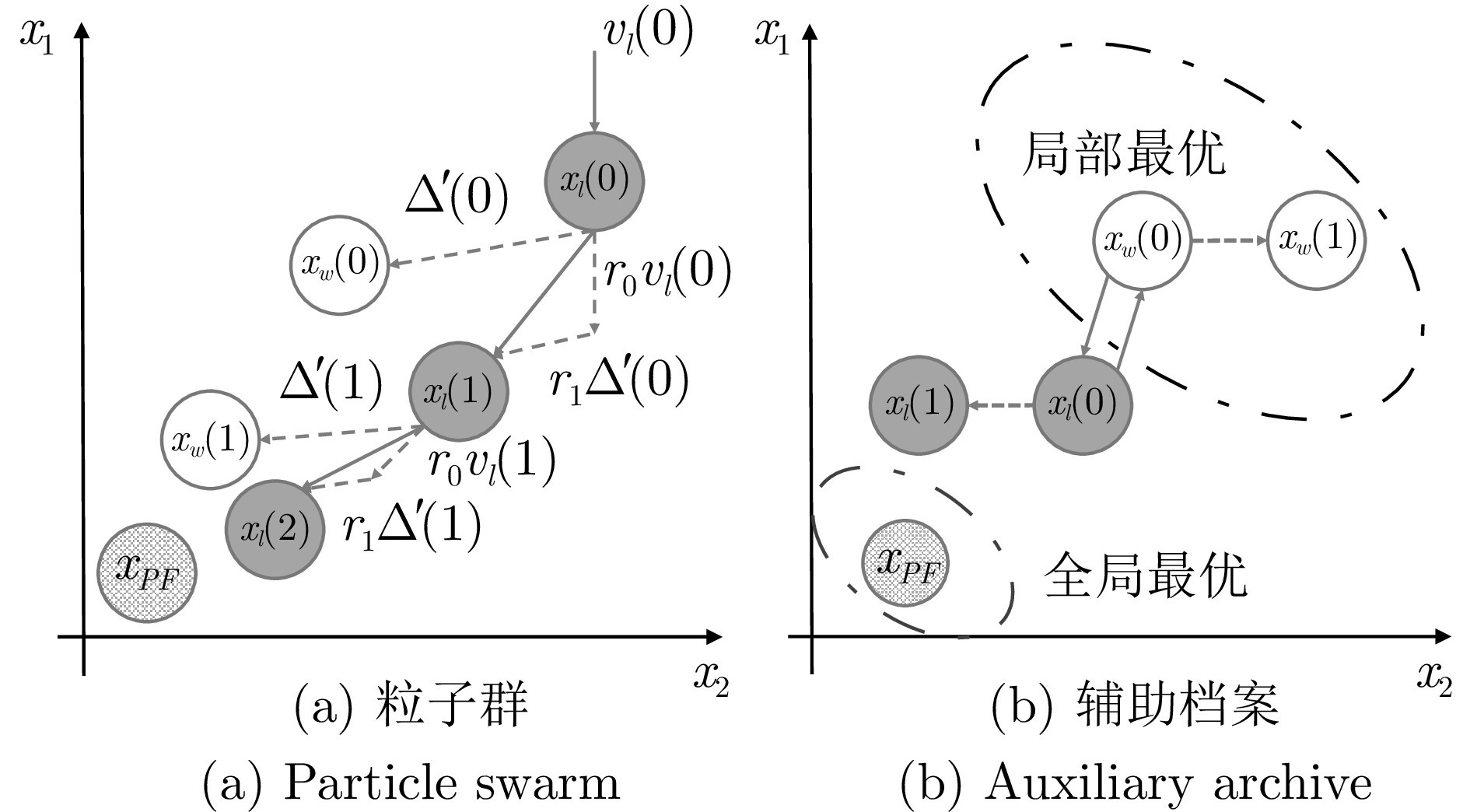
1)提出一种带有辅助档案的粒子群优化器, 主粒子群通过粒子之间的相互学习快速收敛, 辅助档案则通过逃逸机制帮助粒子群跳出局部最优, 以找到完整的约束前沿.

2)提出一种新的ε-约束技术, 结合粒子群进化的特点, 动态减少或增加约束松弛的因子, 使种群在进化初期注重不可行解的遗传信息, 跨越不可行区域; 在进化后期增加约束压力, 重视约束条件的满足, 获得良好的可行解.

3)使用双种群协同进化框架, 引入不考虑约束的参考向量法引导种群进化, 使得种群均匀分布于前沿面, 实现种群的多样性有效维护.

4)本文在当前主流测试集的73个问题上进行实验, 并与现有前沿算法进行比较. 结果表明, 所提出的粒子群优化器能够快速收敛到约束前沿, 并跳出局部最优探索其他区域.

本文其余部分组织如下: 第1节介绍相关工作; 第2节详细进行理论分析并介绍TCCMOA的算法框架和主要构成; 第3节展示TCCMOA和一些前沿算法的性能结果对比及原因分析, 并进行局限性分析; 第4节总结本文工作和贡献, 并对未来工作进行展望.

图1  CMOEA解决约束多目标优化问题的两类典型场景

图2  TCCMOA流程图

图3  粒子群及辅助档案进化机制

进化算法在解决约束多目标优化问题方面表现出色, 然而现有的进化算法面临在解决复杂可行域问题时容易陷入局部最优、难以平衡目标选择和约束满足、多样性维护困难等问题. 在此背景下, 本文提出一种混合算法, 采用弱协同进化框架, 将粒子群的快速收敛特性与参考向量引导策略相结合, 从而得到一种双种群协同进化算法. 本文还设计一种带辅助档案的粒子群学习机制, 利用不可行解的信息以提高种群跳出局部最优的能力. 此外, 本文设计的ε-约束技术能够较好地控制选择压力的缩放, 从而应对各种复杂约束问题. 实验结果表明, TCCMOA在5个基准测试问题集DTLZ、ZXH-CF、LIR-CMOP、MW和DAS-CMOP及真实世界问题集RWMOP上均展现出优异的性能, 证明了其在约束多目标优化领域的竞争力.

然而, 辅助档案的学习机制仍然缺乏稳定性, 导致逃逸机制在MW7、MW11、LIR-CMOP7和LIR-CMOP8这4个子问题上无法生效, TCCM-OA在可行前沿较长的问题上表现不佳. 因此, 未来可进一步引入自适应的位置更新参数来提高粒子群的学习机制的进化效率, 从而加快粒子群在可行域内的扩展速度. 还可改进辅助档案的存档原理与作用时机, 以更加精确地执行逃逸机制, 避免在以上4个子问题中出现种群过分集中的现象.

作者简介

丁炜超

华东理工大学信息科学与工程学院副教授. 主要研究方向为群体智能与演化计算, 多目标优化算法和模式识别. E-mail: weich@ecust.edu.cn

孙立烨

华东理工大学信息科学与工程学院硕士研究生. 主要研究方向为多目标优化及其应用. E-mail: y30230144@mail.ecust.edu.cn

罗飞

华东理工大学信息科学与工程学院副教授. 主要研究方向为分布式计算和智能计算. E-mail: luof@ecust.edu.cn

顾春华

华东理工大学信息科学与工程学院教授. 主要研究方向为人工智能, 云计算, 物联网和信息安全. E-mail: chgu@ecust.edu.cn

董文波

华东理工大学信息科学与工程学院讲师. 主要研究方向为多视图机器学习, 深度高斯过程和多目标优化. 本文通信作者. E-mail: wbdong@ecust.edu.cn