研究背景

在经典的单变量系统频域控制理论中，幅值（增益）和相位这对姐妹概念总是携手同行。系统的波德图由幅值响应和相位响应共同组成，她们在反馈稳定性分析、系统性能评价及控制器设计方面都发挥了同等重要的作用。然而，在多变量系统频域控制理论中，基于幅值的理论硕果累累，基于相位的理论却长期停滞不前，缺乏系统和统一的理论框架。因此，建立一套系统的相位理论填补了频域控制理论中的一个重要空白，为复杂系统的分析和控制提供了新视角和新方法。

相位理论的建立对解决诸多实际问题具有重要意义。研究成果已在多智能体网络、新能源电力系统、通讯网络、多端口电路等方向上得到广泛应用。

成果介绍

香港中文大学（深圳）丘立教授团队建立了一套与幅值理论相对应，适用于复杂系统和大规模网络的相位理论。本文以相论三部曲为主线，全面综述了相位理论在第一个五年的发展历程，发表于IEEE/CAA Journal of Automatica Sinica 2024年第十一卷第八期：D. Wang, W. Chen, and  L. Qiu,  “The first five years of a phase theory for complex systems and networks,” IEEE/CAA J. Autom. Sinica, vol. 11, no. 8, pp. 1728–1743, Aug. 2024. doi: 10.1109/JAS.2024.124542 

一、矩阵相角。定义了（半）扇形矩阵的相角，并系统地研究了矩阵相角的性质。建立了矩阵小相角定理，为反馈系统稳定性分析提供了数学依据。定义了矩阵的本质相角，并提出将Laplacian矩阵本质相角作为网络“非对称程度”的度量。对于强连通图给出了本质相角的显示表达式。提出矩阵相角对齐问题来度量大规模矩阵群体的多样性，并给出了矩阵相角对齐的线性矩阵不等式求解方法。本质相角和多样性度量在异构多智能体网络的同步问题中起关键作用。

二、多变量系统相位理论。定义了多变量系统的相位响应，得到了多变量系统完整的波德图。建立了针对反馈系统稳定性的小相位定理，与著名的小增益定理互补。小相位定理拓展了无源性定理，为基于相位的多变量系统控制理论的建立提供了有力的开端。进一步建立了扇形实引理（与著名的有界实引理对应），给出了系统相位的计算方法。揭示了多变量系统相位在时域上的物理意义。

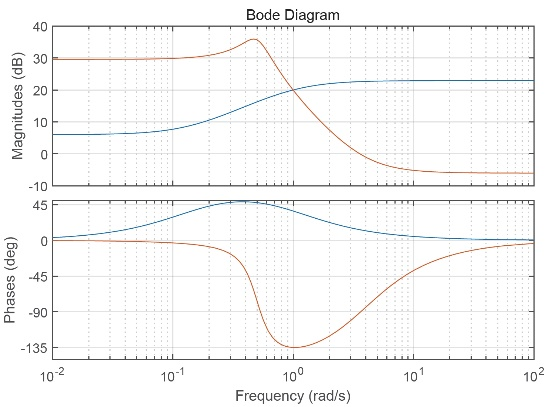
图1  一个二输入二输出系统的波德图

三、基于相位的异构多智能体同步。团队研究了如何设计一个通用可扩展控制器使得多样性群体实现同步。“相角对齐”原则给出同步问题的可解性条件。该条件刻画了群体多样性和网络连接非对称性之间的权衡。网络的非对称性越大，实现同步所允许的群体多样性越小。

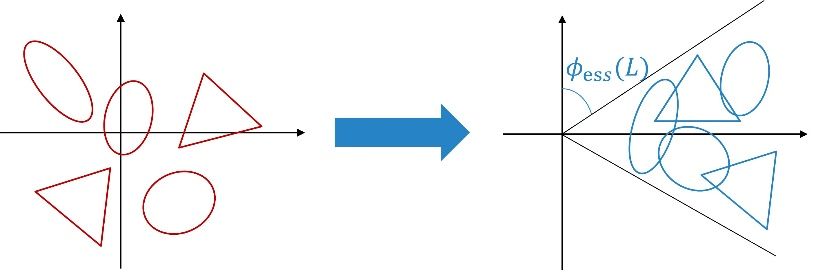
图2  相角对齐示意图

作者及团队

王丹，瑞典皇家理工学院博士后，2020年博士毕业于香港科技大学，主要研究方向包括系统与控制理论，相位理论，大规模网络，新能源电网等。

陈伟，北京大学助理教授，研究员，2014年博士毕业于香港科技大学，2016至2017年于瑞典皇家理工学院及伯克利大学从事博士后研究。主要研究方向包括系统与控制理论，相位理论，网络化控制系统，网络科学，智能电网等。

丘立，香港科技大学荣休教授，香港中文大学（深圳）校长讲座教授，IEEE Fellow，IFAC Fellow。1990年在多伦多大学电气工程系获得博士学位，其后短期工作于加拿大太空署，滑铁卢大学，菲尔兹数学科学研究所，明尼苏达大学数学及其应用研究所。1993年开始在香港科技大学工作，2024年加入香港中文大学（深圳）。丘立教授曾先后担任国际著名期刊IEEE Transactions on Automatic Control以及Automatica的编委，第七届亚洲控制会议大会主席，IEEE控制系统协会杰出讲座团成员，IEEE控制系统协会理事会成员，香港自动控制学会首任理事长。

感谢本文作者提供以上简介