近年来，一致性问题作为多智能体协同控制的基础问题受到广泛关注，其相关理论和技术广泛运用于无人机编队、多机器人系统控制、分布式网络控制等各类任务。尽管大多数已有的一致性协议可以实现渐近一致性，但一些特殊的应用场景要求多智能体系统在有限时间内实现精确一致性。因此，一致性问题中引入了有限时间稳定的概念，形成了有限时间一致性问题。有限时间一致性要求智能体状态在有限时间内达到一致，相较于渐近一致性，具有更快的误差收敛速率、更好的控制精度和更强的鲁棒性。

有限时间一致性的实现通常需要执行机构具有较强的控制能力。然而，在实际物理系统中不可避免地存在输入饱和问题，如果控制器设计时忽略了输入约束，可能会导致控制性能下降甚至闭环系统失稳。因此，考虑输入约束的有限时间一致性问题研究具有重要的现实意义。

澳大利亚斯威本科技大学韩清龙教授和北京航空航天大学左宗玉教授团队提出了一种全新的基于双曲正切函数的多智能体一致性协议，有效解决了一阶、二阶多智能体系统的全局/半全局有限时间一致性问题。研究成果发表于IEEE/CAA Journal of Automatica Sinica 2024年第十一卷第六期：Z. Zuo, J. Tang, R. Ke, and  Q.-L. Han,  “Hyperbolic tangent function-based protocols for global/semi-global finite-time consensus of multi-agent systems,” IEEE/CAA J. Autom. Sinica, vol. 11, no. 6, pp. 1381–1397, Jun. 2024. doi: 10.1109/JAS.2024.124485.

本文所提出的控制协议不仅能够实现有限时间一致性，同时可保证控制输入有界，且其上界可任意预先给定。区别于基于齐次性理论的一致性控制方法，本文可显式给出一致性收敛时间上界的估计值，可离线估计闭环系统的调节时间，给出控制参数的选择方法，该方法具有更好的实际应用价值。同时，运用双曲正切函数代替传统的非光滑饱和函数，有效避免了对各智能体输入饱和状态的分段讨论，显著简化了协议的设计和稳定性的分析。

本文通过数值仿真验证了该一致性协议的正确性，并将该方法应用于多无刷直流电机系统同步控制，验证了其有效性。

图1  智能体之间的通信拓扑

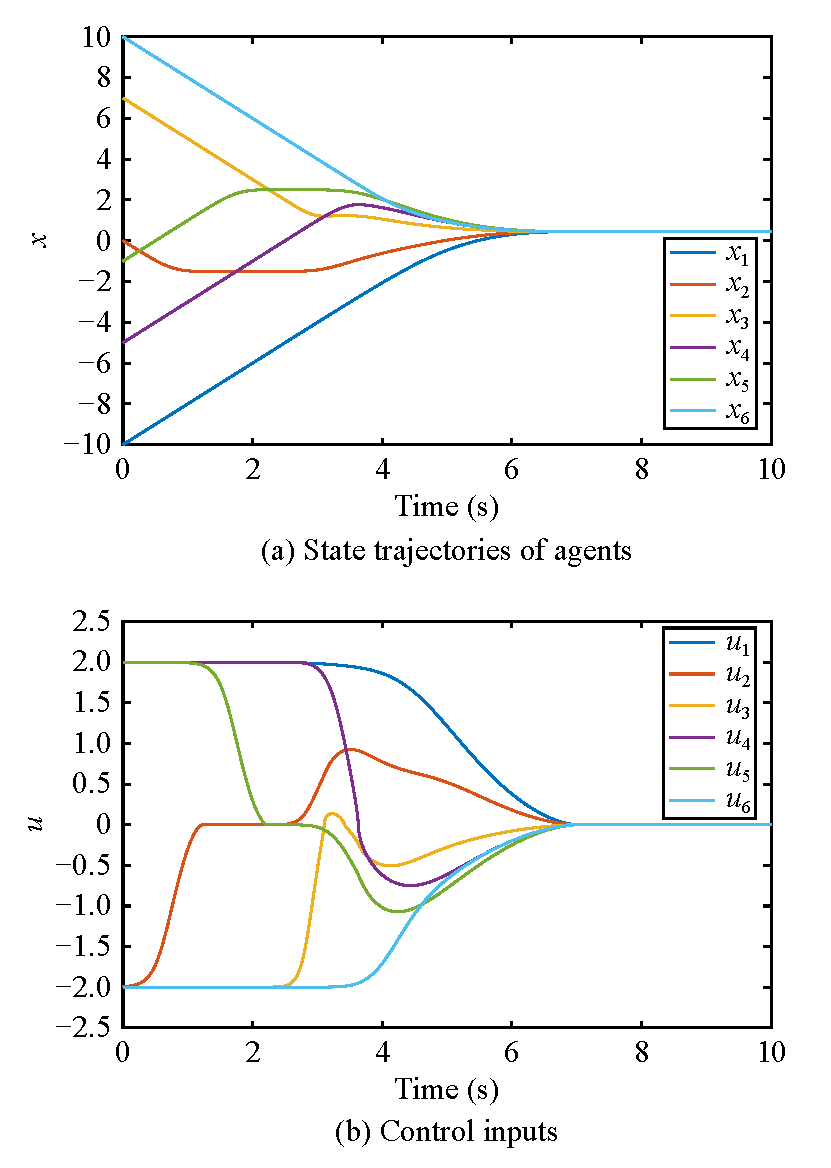
图2  无向图下一阶系统响应

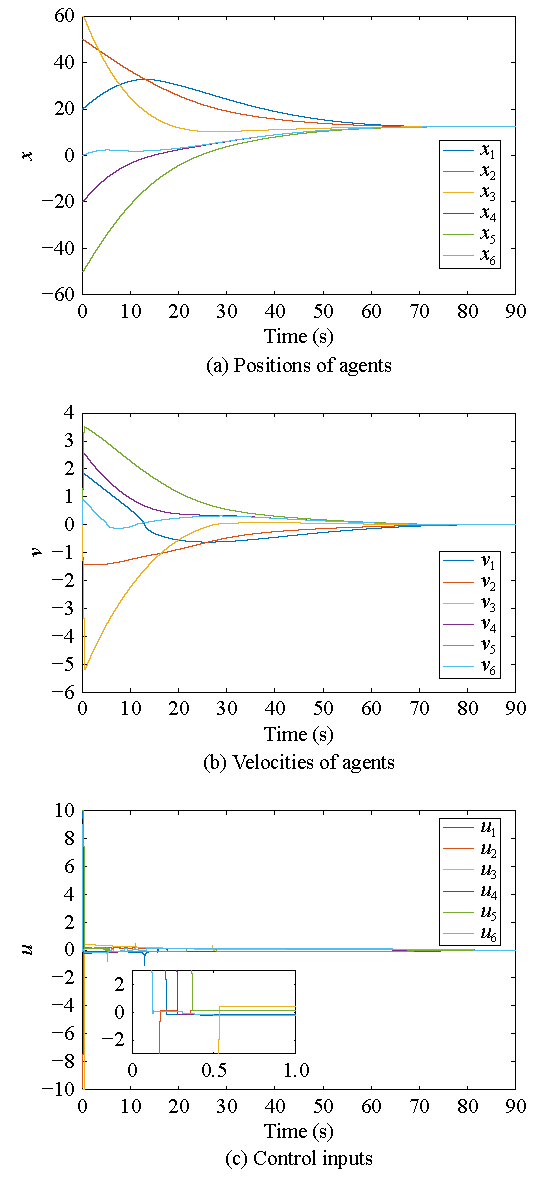
图3  无向图下二阶系统响应

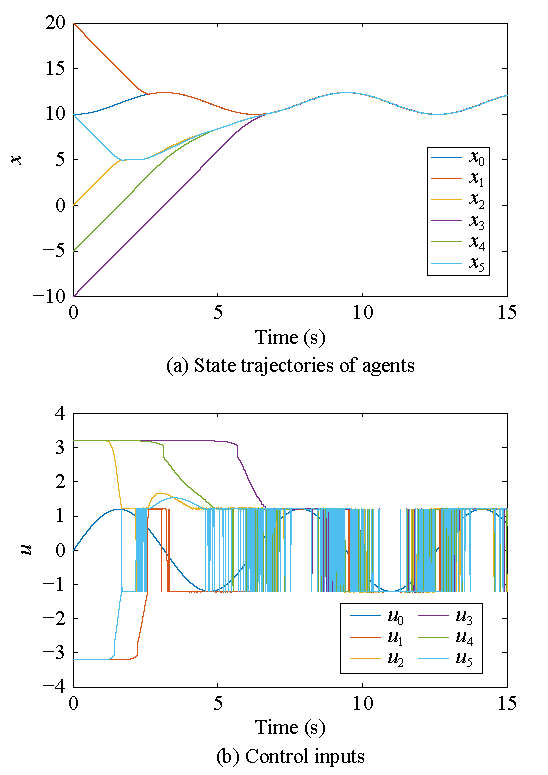
图4  有向图下一阶系统响应

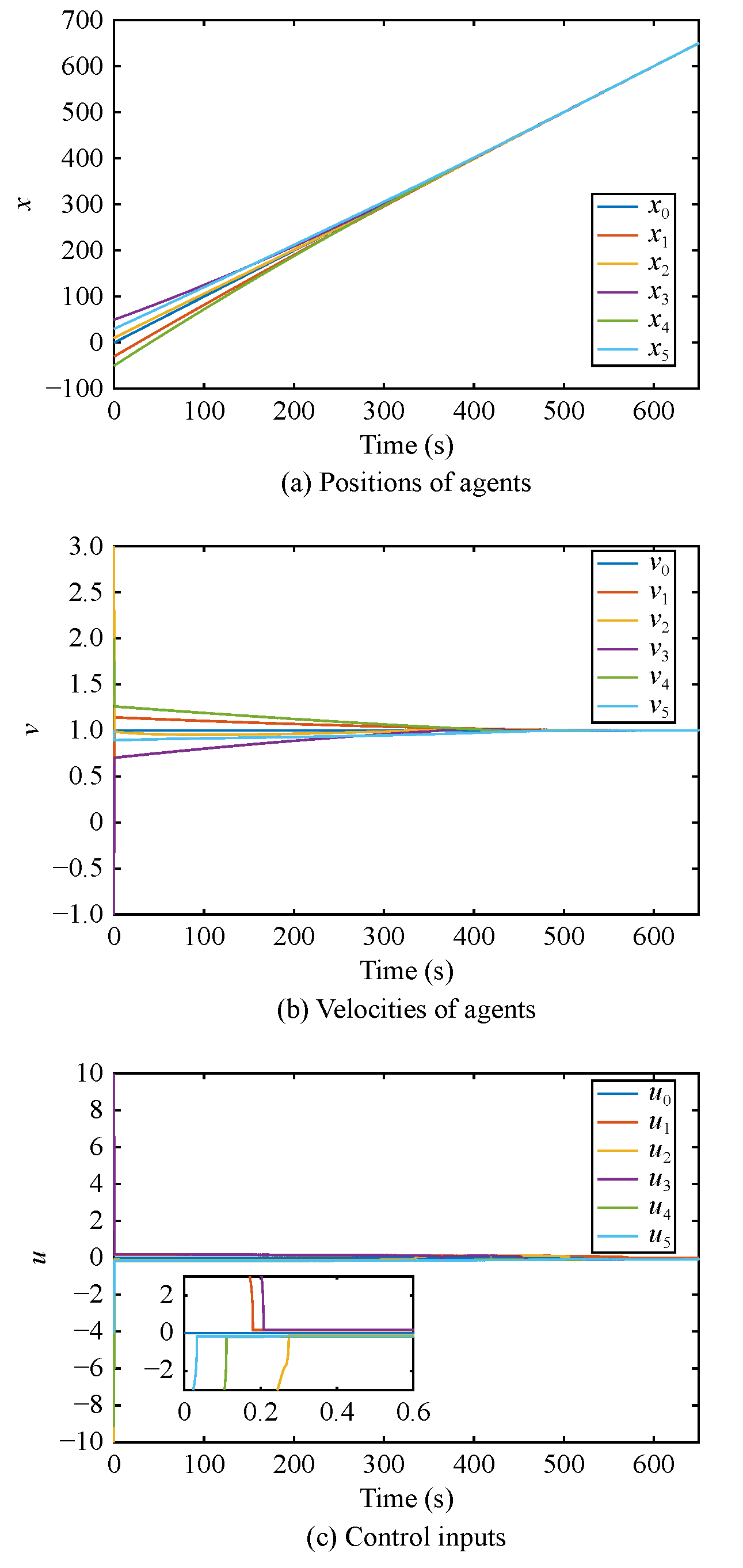
图5  有向图下二阶系统响应

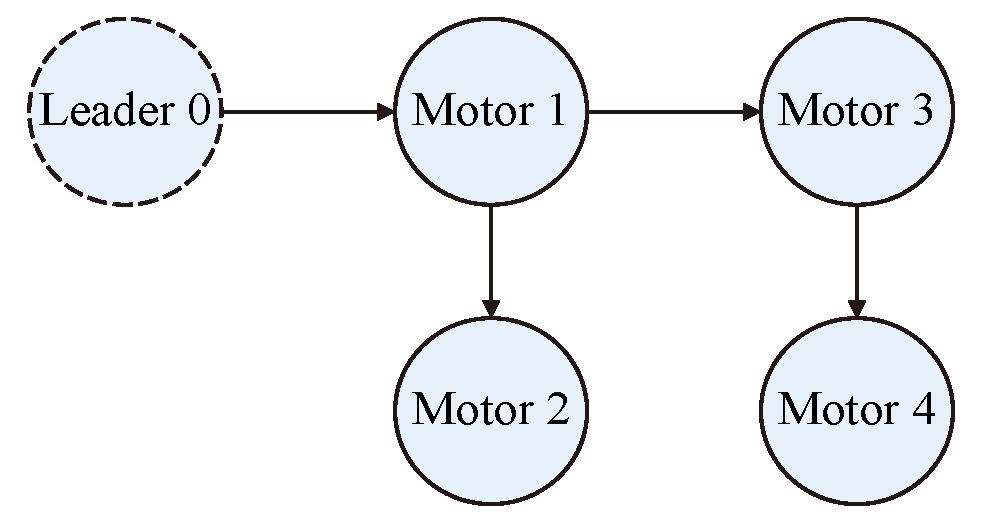
图6  多电机之间的虚拟通信网络

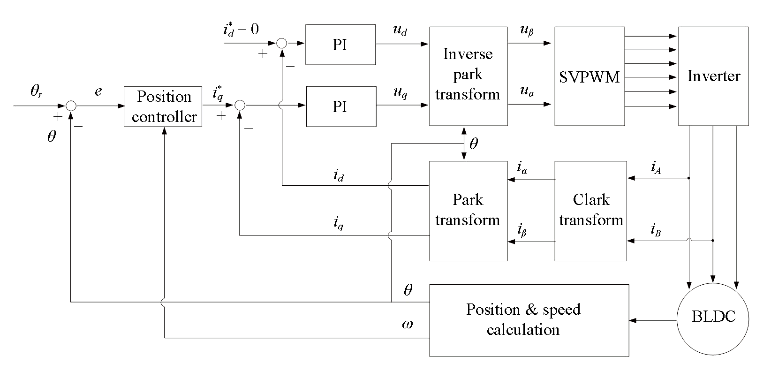
图7  电机位置跟踪系统

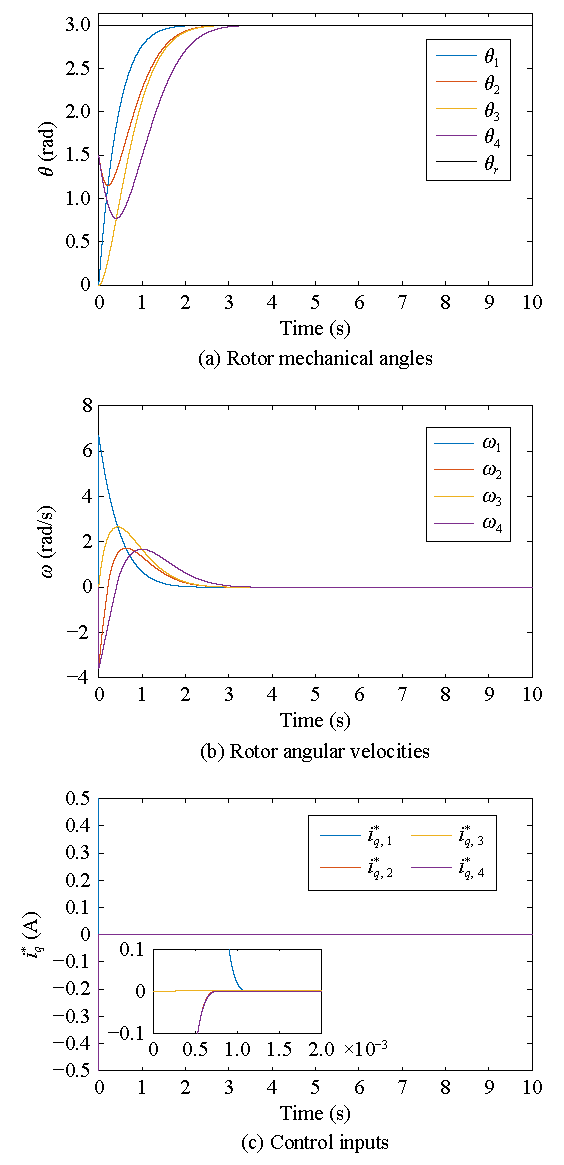
图8  多电机系统响应图

感谢本文作者提供以上简介