学物理的人可能听过一句话：

万物速朽，唯方程式永恒！

世间万物皆难逃岁月的侵蚀，终将消逝于时间的长河之中；但是，宇宙中的物理定律却是永恒的，它们以基本物理方程的形式呈现，不含任何的唯象参数。

然而，如今却有一种观点在悄然蔓延，认为现代物理学已经不具备发现基本物理方程的时机，所以现在一些人更喜欢比拼杂志档次、文章数量等其他方面。

我一直都持有一种观点，若想在物理学领域做出真正原创性的贡献，35岁之前无疑是关键时期。这一阶段是人思维最为活跃的黄金岁月，若在此时未能取得突破，那么往后再想有所作为，概率便会大大降低。十年前，我在科学网曾就这一观点发表过一些博文。不过，也有人持不同看法，认为年轻时应专注于多发表文章，待“功成名就”后再去深入探索原创性课题。

从2009年至今，我大约发表了数十篇物理学论文，涵盖了自旋霍尔效应、量子绝热定理、几何相位、高温超导、统计场论、量子力学基础、拓扑超导、热力学等诸多领域。如今回首过往，这些论文中，真正让我觉得有潜力流传下去的，或许只有两个方程：

第一个方程是虚时间相对论方程[5]

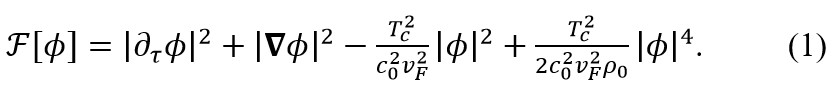
这是描述零温量子相变系统的普适方程，其独特之处在于不含任何唯象参数，且是一个相对论方程，只是其时间变量是虚数。

第二个方程是经典热力学基本方程[13]

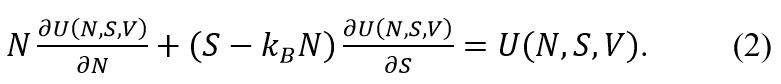
此方程用于描述经典可分辨粒子（例如胶体等软物质系统）的宏观热力学特性，同样不包含任何唯象参数。

在我看来，这两个方程疑似“基本物理方程”。当然，这一推测还需等待实验的最终验证。

基本物理方程的魅力在于其纯粹性——不含任何唯象参数，所涉及的参数均可通过实验精确测量，从而杜绝了人为调参拟合实验结果的可能性。

最纯粹的物理学，本就不应有唯象参数的介入！

最有意思的事情是，这两个方程都是我在2017年发现的，那一年我恰好35岁。只是当时受限于视野，我并未立刻领悟到它们真正的物理价值，且它们最初的形式也远没有如今这般简洁优雅。

方程（1）首次出现在论文[1]，其演变历程可参见论文[1]-[5]；

方程（2）首次见于论文[6]，其演变历程可参见论文[6]-[13]。

真正让我意识到它们可能是基本物理方程，是在七年之后的2024年。此时的我尽管精力大不如前，做基础原创工作的动力在减退，但是对物理学的理解却更成熟。

那么，这两个方程是否会是基本物理方程呢？唯有时间能给出答案。

参考文献：

[1]. Tao, Y. (2017): BCS quantum critical phenomena. Europhysics Letters 118, 57007

[2]. Tao, Y. (2019): Parabolic Scaling in Overdoped Cuprate Films. Journal of Superconductivity and Novel Magnetism 32, 3773-3777

[3]. Tao, Y. (2020): Parabolic Scaling in Overdoped Cuprate: a Statistical Field Theory Approach. Journal of Superconductivity and Novel Magnetism 33, 1329-1337

[4]. Tao, Y. (2020): Relativistic Ginzburg–Landau equation: An investigation for overdoped cuprate films. Physics Letters A 384, 126636

[5]. Tao, Y. (2024): Superconducting quantum criticality and the anomalous scaling: A nonlinear relativistic equation. Physica C 616, 1354424

[6]. Tao, Y. (2018): Swarm intelligence in humans: A perspective of emergent evolution. Physica A 502, 436-446

[7]. Tao, Y. (2020): Self-referential Boltzmann machine. Physica A 545, 123775

[8]. Tao, Y., Sornette, D., and Lin, L. (2021): Emerging social brain: a collective self-motivated Boltzmann machine. Chaos, Solitons & Fractals 143, 110543

[9]. Tao, Y. (2021): Life as a self-referential deep learning system: A quantum-like Boltzmann machine model. Biosystems 204, 104394

[10]. Tao, Y. (2021): Boltzmann-like income distribution in low and middle income classes: Evidence from the United Kingdom. Physica A 578, 126114

[11]. Tao, Y., Lin, L., Wang, H., Hou, C. (2023): Superlinear growth and the fossil fuel energy sustainability dilemma: Evidence from six continents. Structural Change and Economic Dynamics 66, 39-51

[12]. Tao, Y. (2024): From Malthusian Stagnation to Modern Economic Growth: A swarm-intelligence perspective. Journal of Physics: Complexity 5, 025028

[13]. Tao, Y. (2025): Gibbs Paradox and Thermodynamics of Colloids. Physics Letters A 547, 130531