我进入复杂系统这个领域是从研究人类经济行为开始的，如果从2010年在Physical Review E发表此领域的第一篇论文[1]算起，到现在已经有十五年了。在论文[1]中我利用统计物理方法将人类社会看作一个热力学系统来研究，其中一个独特的发现是推导出人类社会的技术进步就是熵。不过2018年之前，我一直将人类社会当作一个“机械物理系统”来研究[2, 3]。真正让我的思想发生转变是在2016年[4]，特别是AlphaGo战胜围棋冠军李世石，这让我开始重新思考智能和生命。这段时间我走出了很关键的一步，认识到技术进步就是人类的群体智能——熵最大即智能[5]。自此之后，我尝试将人类社会看作一个生物系统来研究，并推导出该系统一个可能的基本热力学方程（1）[5]：

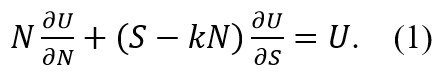
其中N代表人口数量，S代表熵，U代表内能（在人类社会中则为财富总量），k是一个常数因子。

如果将人类个体看作一个“细胞”，几十亿人会不会形成一个超级生命呢？这促使我萌生“社会脑”的想法。我个人猜想，理解智能生命出现的奥秘可能就隐藏在方程（1）中。此后，我的研究主要就是围绕方程（1）进行[6-10]，直到2024年6月我在Journal of Physics: Complexity发表了最后一篇收官论文[11]，自此我觉得对人类社会的研究应该到此为止了——到此时为止（整整6年），我做的人类群体智能的研究仍旧没有激起同行们的兴趣。我甚至认为我终于可以把心思拉回主流经济学研究了。

不过，方程（1）始终有一个困惑影响着我，那就是它解出的熵自动带有吉布斯项lnN!，我曾经将其解释为生物系统特有的自指。我在学术专著《涌现秩序：技术与文明的演化》中专门记录了这个想法，并利用它解释生命的出现。

收官论文[11]发表前夕，我无意中搜索吉布斯项的关键词，看到了PRL上一篇用Jarzynski equality解决吉布斯佯谬的论文。这篇论文提到了一个新的词汇“胶体颗粒”，并强调胶体系统的熵必须带有吉布斯项lnN!。更重要的是，我搜索胶体关键词之后发现，胶体是一种“软物质”，而生命系统的核心组成部分正是软物质！比如，细胞、蛋白质、DNA、生物膜等，都属于软物质。

那一刻我的大脑像是突然被接通了一般，如果把我以前研究的“人类个体”换做“软物质分子”，那方程（1）岂不是恰好就是我曾经所想象的那样——描述生命！

由于方程（1）解出的熵表达式自动带有吉布斯项lnN!，所以刚好解释了胶体系统的熵必须带有lnN!。这个初步想法让我激动不已，我马上到学校图书馆借了马红孺教授的专著《胶体物理导论》利用暑假仔细学习软物质的特征，从而也知道了胶体科学的关键文献。2024年9月我打通了所有的逻辑（在此期间不仅发现了解决吉布斯佯谬的反证法，也严格证明了描述经典粒子的正确熵形式），并写成论文《吉布斯佯谬与胶体热力学》[12]。其中一个有趣的结果是，将方程（1）与广延性（2）结合刚好产生理想气体定律（3）：

我们知道胶体颗粒之间有复杂的相互作用，因此对于软物质系统来说广延性（2）可能是被不同程度破坏的。换句话说，广延性（2）更可能描述极限情形——非生命物质。

按照这个想法，将广延性（2）限制到方程（1）得到理想气体定律（3）就很好理解了。

有了这些激动人心的发现，我于2024年11月初将文章投到Nature Physics和PRL，可惜都被拒稿，没有送审。当时我在PRL尝试申诉到分区副主编，这期间在PRL编辑手上等了3个月左右。直到2025年2月，我决定放弃Physical Review，转投Physics Letters A。这次很快就送审了，大约2个月左右录用。

与我之前的人类群体智能研究不同，论文[12]发表之后我很快就收到国外研究胶体与吉布斯佯谬的同行来信。不久，国内也收到了湖南大学刘全慧教授的来信，他告知我，他和学生在粒子数表象下发现统计力学熵S=k​lnΩ-klnN!的一个等价形式在广延性（他们称为积分形式下的热力学基本方程关系）下与理想气体定律相容，从而推证出理想气体分子的统计不可分辨性（无关量子全同假设）——这是他独特的贡献。我阅读刘教授发来的论文后，意识到这就是我的方程（1）在广延性（2）这种极限情形下的结果。

我论文[12]研究的出发点是胶体这类软物质，最终目的是研究生命系统，所以更关注非广延的情形，对此我的论文[12]给出了一个有待验证的理论预言：

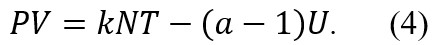
理论预言（4）在平均场意义下成立，对于广延性这种特殊（极限）情形，即a=1，方程（4）就退化为理想气体定律。

刘全慧教授团队的论文出发点是理想气体，不是软物质，所以将理想气体定律作为合意的约束条件。不过在我讲完自己的研究动机之后，刘教授非常赞同将此研究用于胶体这类软物质，可见他的博文《科学网奇缘》。这让我感到很振奋！

以上就是方程（1）的演变由来和历程，我最早将其用于研究人类社会系统，最终发现它最适合描述的是软物质系统——因为软物质分子（比如胶体颗粒）数量庞大，更好的满足统计物理理论的前提假设。

希望国内软凝聚态领域和生物领域的学者可以关注理论预言(4)。这对于弱相互作用的软物质体系应该可以检验——不妨称为玻尔兹曼统计下的理想软物质气体。

参考文献：

[1]. Tao, Y. (2010): Competitive market for multiple firms and economic crisis. Physical Review E 82, 036118

[2]. Tao, Y. and Chen, X. (2012): Statistical Physics of Economic Systems: a Survey for Open Economies. Chinese Physics Letters 29, 058901

[3]. Tao, Y. (2015): Universal Laws of Human Society’s Income Distribution. Physica A 435, 89-94

[4]. Tao, Y. (2016): Spontaneous economic order. Journal of Evolutionary Economics 26, 467-500

[5]. Tao, Y. (2018): Swarm intelligence in humans: A perspective of emergent evolution. Physica A 502, 436-446

[6]. Tao, Y. (2020): Self-referential Boltzmann machine. Physica A 545, 123775

[7]. Tao, Y., Sornette, D., and Lin, L. (2021): Emerging social brain: a collective self-motivated Boltzmann machine. Chaos, Solitons & Fractals 143, 110543

[8]. Tao, Y. (2021): Life as a self-referential deep learning system: A quantum-like Boltzmann machine model. Biosystems 204, 104394

[9]. Tao, Y. (2021): Boltzmann-like income distribution in low and middle income classes: Evidence from the United Kingdom. Physica A 578, 126114

[10]. Tao, Y., Lin, L., Wang, H., Hou, C. (2023): Superlinear growth and the fossil fuel energy sustainability dilemma: Evidence from six continents. Structural Change and Economic Dynamics 66, 39-51

[11]. Tao, Y. (2024): From Malthusian Stagnation to Modern Economic Growth: A swarm-intelligence perspective. Journal of Physics: Complexity 5, 025028

[12]. Tao, Y. (2025): Gibbs Paradox and Thermodynamics of Colloids. Physics Letters A 547, 130531