最快找到最佳路径的最新方法

计算机科学里的一个典范问题是，在一个网络中如何找到去往每个点的最短路径。一种最新的方法打败了教科书里的古典算法。

Ben Brubaker 撰文

左 芬       翻译

【译注：原文2025年8月6日刊载于QuantaMagazine，链接见文末。】

如果你想要解决一个棘手的问题，先把它整理一下往往会有帮助。比如，你可能会把问题分成片段，先处理最简单的片段。不过这种整理会有代价。你可能最终得花大量时间把片段依次排好。

这一困境尤其体现在计算机科学中最具象征性的问题之一：在一个网络中找到从给定点出发到任何其它点的最短路径。它就像是你每次搬家都要解决的一个问题的强化版：找出从你的新家到公司、健身馆和超市的最佳路径。

“最短路径是跟世界上任何人都相关的一个优美的问题，”哥本哈根大学计算机科学家Mikkel Thorup称。

直观来看，找到邻近目的地的最短路径应该是最容易的。因此如果你想要为最短路径问题设计尽可能最快的算法，看起来合理的方式是先找到最近点，接着次近点，以此类推。但是这样的话，你得不断地弄清哪个点是最近的。你会在走的过程中把点按距离排序。遵循这一方式的任何算法都有一个基本的速度极限：你不可能比排序花费的时间更短。

四十年前，设计最短路径算法的研究者们遭遇到了这一“排序壁垒”。如今，一个研究小组设计了一种全新算法，打破了这一壁垒。它并不排序，并且运行起来比任何基于排序的算法更快。

“这些作者敢于认定他们可以打破这一壁垒，”普林斯顿大学计算机科学家Robert Tarjan说道，“这是一项惊人的成果。”

知识前沿

从数学上分析最短路径问题时，研究者使用的语言是图——用线将顶点或节点连接起来的网络。节点间的每一条边都标记有一个叫做权重的数字，它代表着该线段的长度或者经过它所需要的时间。在任意两个节点间通常有很多路径，权重加和之后数值最小的就是最短的。给定一个图和一个特定的“源”节点，算法的目标是找到通往任何其它节点的最短路径。

最短路径最著名的算法是由计算机科学先驱Edsger Dijkstra 1956年开发的，从源出发逐步地往外推进。它是一种有效的方式，因为知晓到近邻节点的最短路径可以帮助你找出到更远节点的最短路径。可是由于最终结果是一个最短路径的有序列表，排序壁垒就给这一算法的速度设置了一个基本极限。

1984年，Tarjan和另一个研究者改进了Dijkstra的原始算法，让它达到了这一速度极限。任何进一步的改进将不得不出自绕开排序的一种算法。

1990年代末到2000年代初，Thorup和其他研究者开发了打破排序壁垒的算法，但他们必须对权重做出某些假定。没人知道如何将他们的技术推广到任意权重情形。似乎他们已经走到了路的尽头。

“这一研究停滞了很长一段时间。”位于北京市的清华大学的计算机科学家段然说道，“许多人认为不可能有更好的方法了。”

段并不这么想。他一直梦想着构造出能在所有图上打破排序壁垒的最短路径算法。去年秋天，他终于成功了。

超出排序

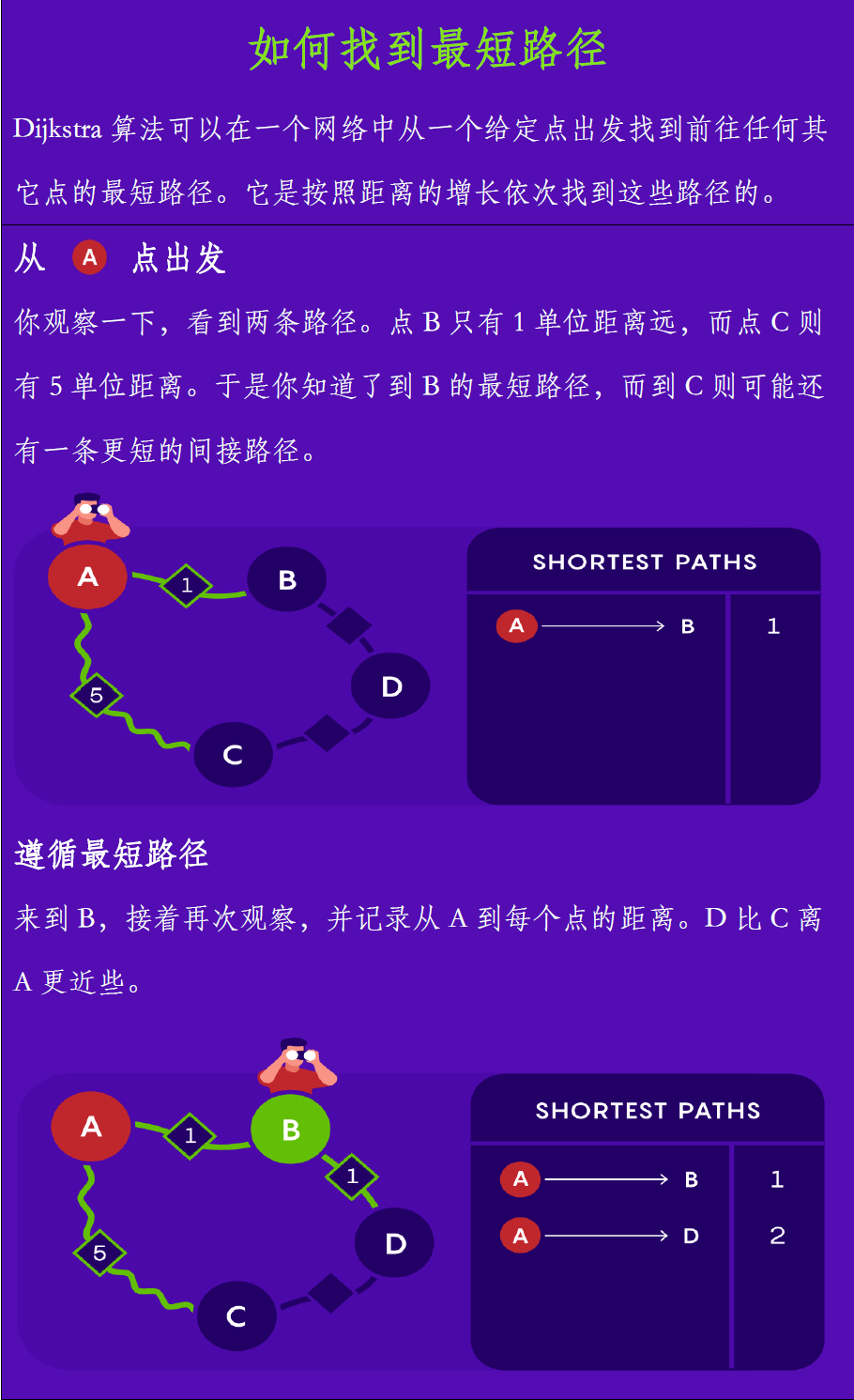
Edsger Dijkstra开发了一个经典的算法，可以在一个网络中从给定点出发找到前往任何其它点的最短路径。

段在排序壁垒上的兴趣可以追溯到近20年前在密歇根大学的研究生时期，当时他的导师是在特定情形下成功打破壁垒的研究者之一。不过直到2021年段才设计出一种更加有希望的方案。

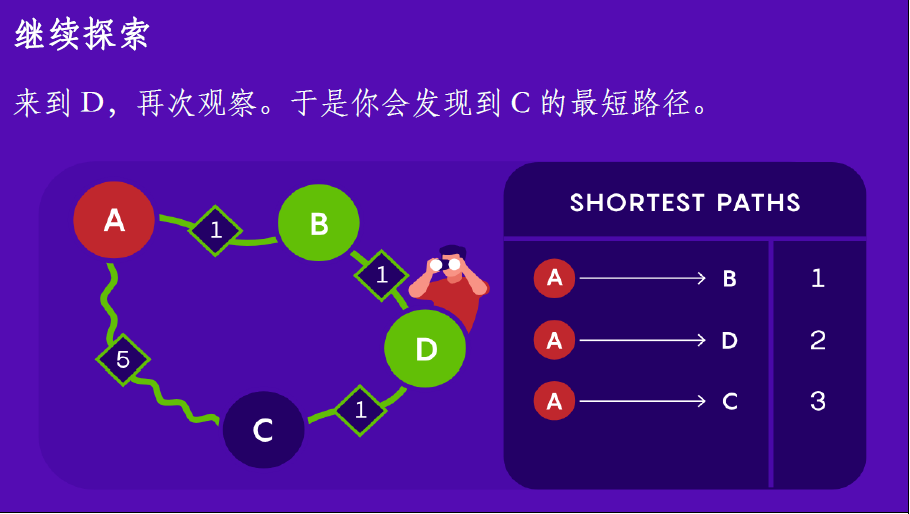
关键在于要关注算法在每一步会接着去往何处。Dijkstra算法是以先前步骤已经探索过的区域为出发点的。它通过扫描这一区域的“前线”——也就是，连接到它的边界的所有节点——来决定下一步去哪儿。这在一开始不会花费太多时间，但随着算法的进行会越来越缓慢。

段则是考虑把前线中的近邻节点分组成团簇。接着他会在每个团簇中仅仅考虑一个节点。这样要筛选的节点就少了，因此每一步的搜索会快得多。算法也有可能去到最近节点之外的位置，所以排序壁垒不再起作用。但是要确保这一团簇方法实际上会让算法加速而不是减速则具有挑战性。

段在接下来一年里对这一初步想法加以充实，而到了2022年秋天，他已经很有信心可以克服技术上的障碍。他拉拢了三个研究生来协助完成细节，并且在几个月后他们得到一个部分解——可以在任意权重下打破排序壁垒的一个算法，但只对所谓无向图适用。

在无向图中，每条边都可以往返经过。计算机科学家往往对更广泛的由单程线组成的图更感兴趣，但这些“有向”图通常更难以驾驭。

“可能会有这样的情形，A可以很容易地到达B，但B却无法很容易地到达A，”斯坦福大学计算机研究生毛啸说道，“这会给你带来大量麻烦。”

有望之路

2023年夏天，毛在加州一个会议上听段做了一个关于无向图算法的报告。因为一直很钦佩段的工作，他抓着段聊了一会。

“这是我在现实生活中头回见到他，”毛回忆道，“太让人激动了。”

在那次会议后，毛开始在空闲时间思考这一问题。与此同时，段与他的合作者也在探索可以用于有向图的全新方法。他们从最短路径问题的另一个古老算法，所谓Bellman-Ford算法中获得了灵感，而这个算法也不会生成一个有序列表。咋一看，这似乎不像是个明智的策略，因为Bellman-Ford算法比Dijkstra算法要慢得多。

“你在做研究时，总会试图选择一条有希望的路线，”Thorup说道，“而选择Bellman-Ford，我简直会把它视作无望的，因为它看起来完全就像是你能采取的最笨的方法。”

段的小组设法避免了Bellman-Ford算法的缓慢，采取的策略是每次只运行它少量几步。对Bellman-Ford的选择性使用使得他们的算法可以提前侦查到后续步骤中要探索的最有价值的节点。这些节点就像是一个道路网络中主要干道的交叉点。

“你必须途径【它们】才能获得前往大量其它地点的最短路径。”Thorup说道。

2024年3月，毛想出了另一种有望的途径。在团队原始方法的某些关键步骤上使用了随机性。随机化算法可以有效地解决大量问题，但研究者们仍然倾向于非随机方法。毛发明了一种新方法，可以不引入随机性就解决最短路径问题。他加入了团队，接着大家在之后的数月里通过群聊和视频通话协同工作，来融合各自的想法。最终，在秋天的时候，段意识到他们可以采用他在2018年为了对另一个图论问题打破排序壁垒而设计的一个算法中的一种技术。这种技术充当了他们需要的最后一块拼图，让他们得出了在有向和无向图上都能快过Dijkstra的算法。

最终的算法会把图切成片层，并跟Dijkstra算法一样从源点往外移动。不过它不再在每一步都处理整个前线，而是采用Bellman-Ford算法来确认显著节点，并从这些节点往外找出前往其它点的最短路径，并在之后返回其它前线节点。它对每一层的节点并不总是按照距离增长来依次搜索的，因此排序壁垒不起作用。并且如果你以适当的方式对图切片，它会比Dijkstra算法的最佳版本还要快一点。它要复杂得多，需要把许多个片段恰到好处地拼在一起。可是神奇的是，这些片段中没有哪一个用到了高超的数学。

“这种结果完全有可能在50年前就被发现，可是并没有，”Thorup说道，“这就使得它尤为引人瞩目。”

段和他的团队打算探索这一算法是否可以进一步精简，让它变得更快。在打破排序壁垒后，新算法的运行时间还没有邻近任何计算机科学家知晓的基础极限。

“作为一个乐观主义者，如果你能进一步缩减时间我会毫不惊讶，”Tarjan说道，“我当然不认为这会是整个进程中的最后一步。”

原文链接：

https://www.quantamagazine.org/new-method-is-the-fastest-way-to-find-the-best-routes-20250806/