一对扭曲形状解决了一个拓扑学世纪难题

Bonnet问题指的是，何时一丁点信息就足以唯一地确定整个曲面。

Elise Cutts  撰文

左  芬    翻译

（译注：原文2026年1月20日刊载于QuantaMagazine， 链接见文末。）

史无前例地，数学家发现一个甜甜圈样的曲面（如上所示）跟另一个曲面具有相同的局域几何信息，但它们的全局结构却完全不同。

想象如果我们的天空始终被厚重的乌云覆盖着。在没办法看到星星，也没办法从空中往下俯视的前提下，我们是否会发现地球是圆的呢？

答案是会。通过测量地面上特定的距离和角度，我们可以确定地球是一个球面，而非比方说平面或者甜甜圈形的——哪怕没有卫星图像。

数学家发现这对于更一般的二维曲面也往往是对的：曲面相对少量的局域信息就足以让你知晓它的整体形状。局部唯一地界定了整体。

可是在某些异常情形下，这一受限的局域信息可能描述了多于一个曲面。数学家们花了过去的150年来登记这些异常：通常只界定一个曲面的局部测度事实上却描述了多于一个曲面的情况。可是他们设法找到的仅有异常都不是像球面或者甜甜圈那样良好的闭合曲面——相反，它们会在某个方向一直延伸下去，或者带有你会掉下去的边缘。

没有人找到能打破这一规则的闭合曲面。看起来这样的曲面可能根本就不存在。或许闭合曲面总是可以由常规的局域信息来唯一地界定。

如今，数学家终于发现了这些求索已久的异常之一。在去年十月发表的一篇论文中，柏林工业大学的Alexander Bobenko、慕尼黑工业大学的Tim Hoffmann以及北卡罗莱纳州立大学的Andrew Saeman-Furnas三人给出了一对非常扭曲的闭合曲面，证明它们拥有相同的局域信息但完全不同的全局结构。

找出它们花费了数年的辛勤劳作，烧坏了几台笔记本电脑，还从一个看似没有关联的几何学角落获得了一个始料未及的线索。

几何不适

数学家有各种各样的方法来局域地刻画一个曲面，但其中的两种格外有用。

一种体现了曲面的“外在”曲率的信息。在你的曲面上选一个点。在那个点上，有无穷多个方向让你去计算曲面在空间中的弯曲程度——也就是所谓的曲率。只聚焦到你得到最大和最小曲率值的方向上，并取二者的平均。你得到的数值被称为平均曲率。你可以在曲面上的任何给定点上计算出平均曲率，从而更好地理解它在周围空间中的处境。

另一种度量体现的信息是曲面的“内在”曲率——不依赖曲面所处空间的一种几何性质。考虑一张平展的纸。你无需拉伸或撕裂它，就可以把它卷成一个圆柱管。如果在纸上有两个点被一条曲线连着，那么这条曲线在圆柱面上会有同样的长度。这意味着纸张和圆柱面有着相同的“度规”，也就是距离的概念。可当你试图把纸张裹在球面上时，情况就不是如此了。你不得不拉伸、剪开或是揉皱纸张，这样点之间的曲线的长度就会改变了。因此这两个曲面具有不同的度规。

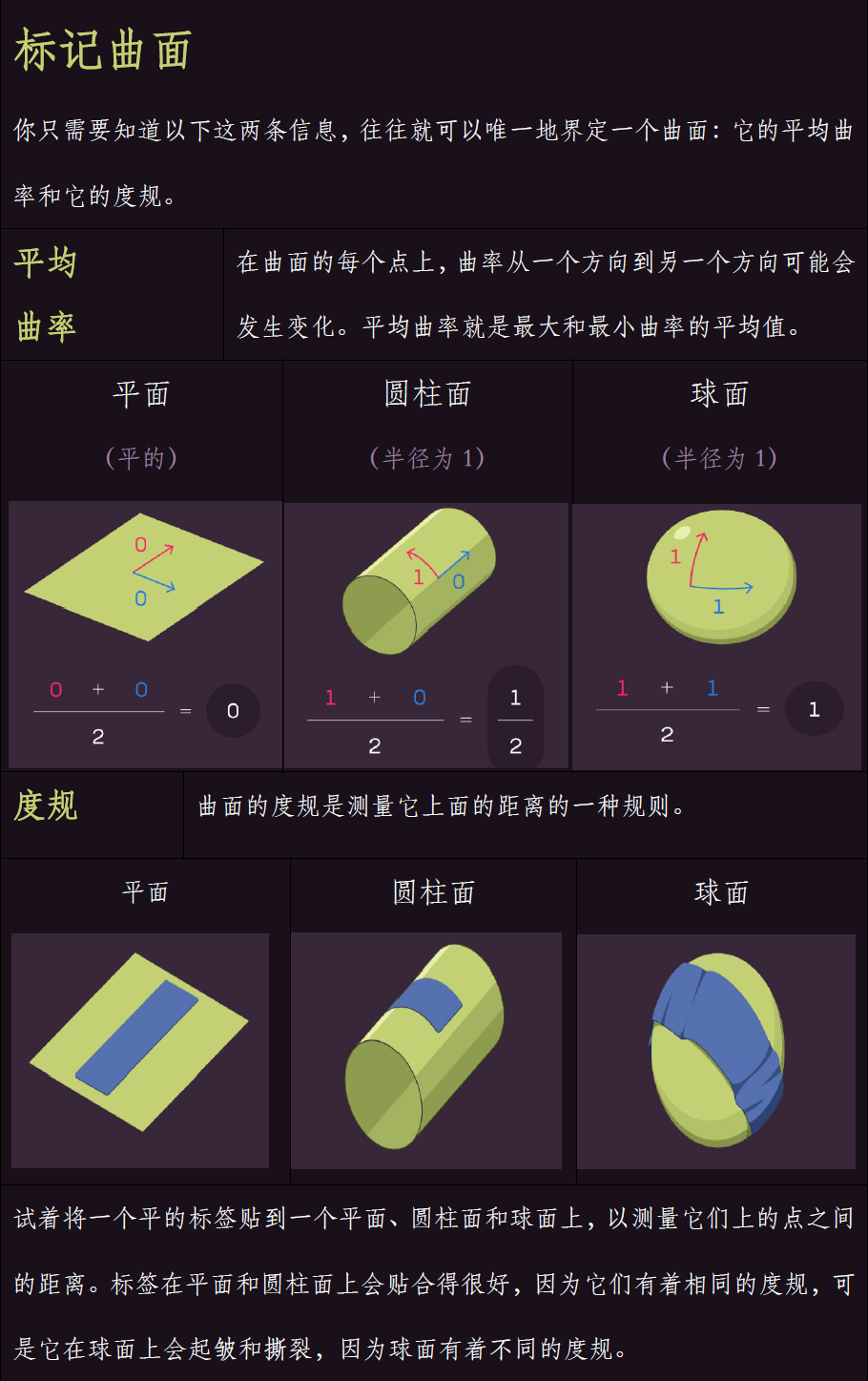
1867年，法国数学家Pierre Ossian Bonnet证明，如果你知道曲面上每个点的度规和平均曲率，就足以给出曲面的形状了。大多数时候是这样。

可大多数时候毕竟不是所有时候，而正是这种受限让数学家感到不安。

在Bonnet的证明出来之后的150年里，数学家们发现有各种各样的曲面会违背他的经验规则。这些曲面有着相同的度规和平均曲率，但它们的整体结构并不相同。

Pierre Ossian Bonnet所问的是，是否可能用相同的局域数据定义出两种不同的形状来。

可是所有这些曲面都是数学家所谓的非紧曲面。它们不会像球面、甜甜圈以及其它“紧”曲面那样很好地包裹起来。相反，一个非紧曲面可能会（像平面或者圆柱面那样）在某个方向无限地延伸下去，或者（就像从一个更大的形状上切下的一块那样）具有突然终结的边缘。

紧曲面更受限。它们必须满足各种约束，才能绕回到自身，并完好地闭合上。因此我们似乎可以合理地认为它们可能会被度规和平均曲率唯一地界定。1981年，数学家Blaine Lawson和Renato de Azevedo Tribuzy证明对于球面和拓扑等价于它的任何曲面——也就是说，任何没有洞的紧曲面——这一结论是成立的。

当涉及带有一个洞的紧曲面（拓扑甜甜圈，也就是所谓环面），情况有点回旋的余地。这些数学家证明一种给定的度规和平均曲率可以对应到至多两个不同的环面。

可是，没有人能找出这种“紧Bonnet对”的实例，因此数十年来，主流观点认为环面就跟球面一样，给定度规和平均曲率会界定出单一的环面来。“在很长一段时间里人们都相信这一点，”杜克大学的Robert Bryant说道，“因为他们就是没法构造出任何实例来。”

可是他们都错了。

像素化世界

Alexander Bobenko已经花了过去20年啃这些数学甜甜圈。2000年代时，他试图证明紧的Bonnet对确实存在。可是在意识到这一问题会花费他好几个月才能解决后，他把它丢到了一边，转而聚焦到别的他觉得可以更快取得进展的问题上去了。

他转到了看起来跟Bonnet问题无关的一个数学领域里。可是这个领域最终却成为了解决它的关键。

Bobenko开始思考“离散的”曲面，这些有点像光滑曲面的低分辨率的像素化版本。数学家们研究离散曲面，是因为它们本身就拥有重要的几何性质，并且在诸如计算机科学、物理学、工程学等学科中具有实际用途。

要得到离散曲面，取一组有限的点，然后把它们用线段连起来，构成带有多个平坦面的形状。通过选择不同的点，你可以用不同的方式来表征一个给定的光滑曲面。例如，以下是球面表征方式的一些例子：

有些离散曲面比其它的表征得更好。Bobenko和他频繁的合作者Tim Hoffmann投入了接近二十年来发展这方面的理论，以使离散曲面保持光滑曲面最突出的几何特征。

到了2010年代，那时还是哥廷根大学博士生的Andrew Sageman-Furnas加入了团队——并且把Bonnet问题又带回到了这群人中。

Sageman-Furnas会被吸引到离散数学里，是因为他对渔网这类织物的结构很感兴趣，而这些本质上就是离散的曲面。在这一过程中，他提出了Bonnet问题的离散版本：何时局域信息会唯一地界定一个离散曲面，何时不会？通过改造一种生成Bonnet规则异常的已知方法，Sageman-Furnas与他的导师Max Wardetzky以及Hoffmann一同找出了一种配方，可以在离散情形下调制出异常来。

就跟光滑情形一样，这些异常往往也是非紧的。不过因为离散曲面不会包含无穷多个点，可以使用计算机去研究它们。Sageman-Furnas好奇，有没有可能使用暴力的计算方法在离散几何的国度里找到紧的Bonnet对呢？如果可能，那么或许离散情形还可以为光滑解指明方向。

于是他到柏林加入了Bobenko和Hoffmann，成为Bobenko团队的一名博士后研究员，并开始工作。

曲面狩猎

2018年春天，Sagemann-Furnas开始用计算机搜索一种特定类型的曲面——这种曲面可以转变成Bonnet对，就像用酵母面团作为基础制作出不同种类的面包一样。这一“面团”曲面会类似于他在研究生时用来得到离散Bonnet对所使用的那些。只不过这一次，他想让它是一个环面。也就是说，它必须是紧的，并有一个或更多的洞。

他消失了好几周，甚至可能数月，Hoffmann回忆道。当这个年轻数学家终于再次出现时，他已经找到了他一直搜索的东西：一个非常尖利的形状，看起来更像是一个折纸犀牛而不是一个环面。

“犀牛”

可它确实是一个环面。并且依照Sageman-Furnas的计算机程序，它还拥有生成Bonnet对的面团曲面所需要具备的所有其它性质。而更重要的是，当Sageman-Furnas在他的电脑上生成这些对后，它们全都是环面。从犀牛到Bonnet对的转换似乎并不会把犀牛扭开成非紧曲面。曲面保持是紧的。

“当你开始做计算机探索和设计时，” Sageman-Furnas说道，“你会得到新的例子，远远超出你之前觉得可能的。”

可这是不是好得有点不现实了？计算机程序会产生取整错误：Sageman-Furnas的犀牛可能看起来满足所要求的判据，并且它生成的Bonnet对也看起来是环面，但这可能全都是海市蜃楼，是小的计算错误造成的假象。在没有严格证明之前，数学家不能确定。

“他出现了，给我们展示了一些诡异的几何物体，看起来真的很像是数值垃圾，”Hoffmann说道。“开个玩笑，可能在整个项目中我最重要的贡献就是当时我说了一句，‘这还不算太差。’”

Andrew Sageman-Furnas（左），Tim Hoffmann（中）和Alexander Bobenko构造出一对新奇的形状，解决了一个长久以来的猜想。

Hoffmann和Sageman-Furnas花了一些时间，最终让自己确信这个犀牛值得认真对待。并且既然能够找到离散Bonnet对的这样一种可能性很大的实例，或许光滑情形最终也不是说完全没有希望。Hoffmann和Sageman-Furnas接下来那个闷热的夏天都用来检查犀牛上的线索，有时一次就视频通话8到12个小时，以搜寻独特的性质和几何上的约束来帮助他们缩小寻找光滑Bonnet对的范围。

随着九月的到来，他们最终找到了一条感觉很有希望的新线索，而这也把Bobenko带回了他在数十年前抛弃的这一问题当中。

闭环

这一线索跟沿着犀牛的边来环绕犀牛的特定线条有关。

人们已经知晓这些线条会提供犀牛的曲率方面的重要信息，会追踪出它弯曲和折返得最厉害和最轻微的方向。因为犀牛是生活在三维空间中的二维曲面，数学家们预期这些线条会在整个三维空间中都划出路径来。可是不然，它们总是要么处在一个平面内，要么在一个球面上。几乎不太可能这些排布是偶然发生的。

“这向我们表明，确实有一些特殊的事情发生了，”Sageman-Furnas说道。这让人“惊叹不已”。

跟离散曲面不同，光滑曲面没有边。不过你仍然可以画出追踪最大和最小弯曲路径的“曲率线”。Sageman-Furnas, Bobenko与Hoffmann决定寻找犀牛的一个光滑类似物，把它的曲率线也类似地约束到平面或球面内。或许具有这些性质的面团曲面会给出光滑的Bonnet环面来。

但这样一种曲面是否存在甚至都不明朗。

Jean Gaston Darboux提出的公式在100多年后成为了研究Bonnet问题所缺失的环节。

接着Bobenko意识到，在一个多世纪前，法国数学家Jean Gaston Darboux就已经给出几乎刚好是这些数学家现在所需要的工具。

Darboux提出过一些用来生成曲面的公式，使得曲面正好拥有这类曲率线。问题在于，他的公式生成的曲率线不会绕会到它们自身。相反，它们“看起来像螺旋线，会去往无穷远，”Bobenko说道，“没法让它们闭合起来。”这意味着尽管曲率线可能处在平面和球面内，整个曲面不会是一个环面。

经过多年劳作，这些数学家——通过结合手算和计算机实验——想出了办法来改造Darboux公式，使得曲率线会闭合起来。他们最终找到了犀牛的光滑类似物（尽管二者看起来不怎么像）。

此外，如同他们希望的那样，这个光滑的犀牛可以生成一对新的环面，它们具有相同的平均曲率和度规，但整体结构并不相同。团队终于找到了原始Bonnet问题的答案：有些环面终归不会被它们的局域特征唯一地界定。

可是当弄清这个Bonnet对真实的样子时，他们发现这两个环面其实是彼此的镜像。“技术上来说，这不成问题，”Sagaman-Furnas说道，“形式上，我们已经解决了这个问题。”可是，他补充道，这还不是那么令人满意。

因此在接下来的一年里，他们用各种各样的方式微调他们的光滑犀牛。最终，他们意识到，只要他们去掉一组曲率线必须处在球面上的要求，就可以构造出一个满足需求的全新光滑犀牛。他们接着使用这一曲面去生成一个新的Bonnet对——这一次，得到的是两个非常扭曲的环面，它们的形状是截然不同的，但仍然具有相同的度规和平均曲率。

团队最终得到的紧Bonnet对。

对于马萨诸塞大学阿默斯特分校数学家Rob Kusner来说，这一结果有些出乎意料。在他看来，这表明哪怕环面——最良好、研究最透彻的曲面中的一种——也不是总能由它们的局域特征刻画。

“这个例子告诉我们，在有些情况下我们的直觉是不够好的，”杜克大学数学家Bryant称。

不过，这些数学家发现的这两个环面有点古怪：它们会像数字8一样穿过自身。 Bobenko现在希望证明存在不贯穿自身的Bonnet环面对。

这一Bonnet环面对是对Bobenko和Hoffmann在离散曲面上数十年工作的欣然肯定。传统上，光滑形状的几何发展得快得多，拖着身后发展迟缓的离散几何前行。可是在这一工作中，离散几何冲锋在前，并最终使得光滑方面的进展成为可能。

在Hoffmann看来，这凸显了一个事实，那就是尽管离散曲面可能看起来像是其光滑副本不怎么精巧的模型，它们拥有自己的数学生命。离散世界可以跟光滑世界一样丰富，甚至有过之而无不及，并能揭示从其它途径可能丢失的额外对称性和关联。

“人们有点遗忘了这一离散视角，”Hoffmann说道，但“从它依然可以获取许多信息。”

原文链接：

https://www.quantamagazine.org/two-twisty-shapes-resolve-a-centuries-old-topology-puzzle-20260120/