博文
地球系统力学动力学(2)
|
地球系统力学动力学(2)
李务伦
吉林省煤田地质局二零三勘探队
第二部分 上升力与下降力及浮力产生的数理根源[17]
这一章主要解决浮力产生的数理凭据,用以下的步骤解答:1、给出异密度物进入球内后的引力场特征;2、从引力场的特征分析异密度物的上升与下降的产生力场原因;3、给出异密度物上升力和下降力的计算公式;4、给出浮力的本质及表达式。5、异密度物进入球后造成稳定平衡力场扰乱引起的物质运动动力学。
1、引言
异密度物体存在于流体中,要么下降要么上升,是常见的物理现象。物体下降、上升产生的原因是物体存在浮力的缘故。流体变为固体,浮力还存在吗?若此浮力不存在,盐丘[1]、底劈(穹窿)一类地质构造现象又该用怎样的理论解释呢?两千多年前浮力被华夏先贤完成发现以来,因无生产科学实践的更大需求,即便万有引力定律被发现,长期以来没有人对浮力产生的数理原因进行探究。然而,是否可以从数理上推出浮力产生存在?答案是肯定的,是本部分的重点。解决这一问题将以万有引力定律或引力场为基础,找出浮力产生的数理根据。在解决这一问题同时,可以看到围绕这一问题,得到以不同参数角度下的动力学。
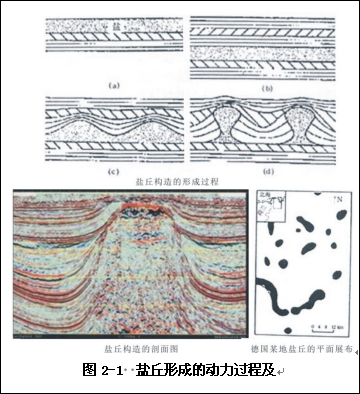
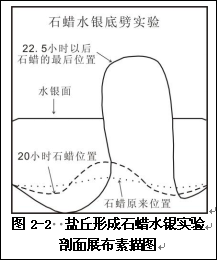
图2-1展示了盐丘形成过程图[1]、盐丘地震剖面图和盐丘平面图[2]。盐丘、底劈(穹窿),是常见的地质地质构造。为解释这类现象,昆明地质学校主编的《构造地质及地质力学》教材中[1],对盐丘形成是这样解释的:“盐丘上升的动力是岩盐与上覆岩层的密度差,比一般沉积岩轻的岩盐向上移动时,就像一种较轻的液体穿过盖在它上面的较轻液体一样。有人用石蜡和水银作模拟实验,在一个容器下部放上石蜡,上覆以水银。经过22.5小时后,石蜡刺穿了水银面,得到了与盐丘类似的构造形态图(见图2-2[1])”。再看,图2-3右侧是中国空间站燃烧的蜡烛也为球形,与地球上点燃的蜡烛相差别很大。这都是为什么?
上面对盐丘的形成给出了比喻加实验的解释,可以看到地学工作者即想用浮力解释,又不敢用浮力解释。这是因为浮力(阿基米德定律或阿基米德原理)表述是:浸在静止流体中的物体受到流体作用的合力等于该物体排开的流体重力,方向竖直向上,数学表达式: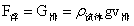 。浮力去掉物体重力
。浮力去掉物体重力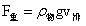 得浮力与物体所受重力差:
得浮力与物体所受重力差:![]() ,该式中ρ流体大于ρ物,物体上浮,否则下沉。因此上述对盐丘,底劈(穹窿)构造形成的解释是尴尬的!该如何解释这类构造呢?是否可以用浮力解释以上构造现象,下面对浮力的通过引力场理论的求解,可以回答以下问题:1、明确的回答浮力与是否为流体无关;2、浮力仅能称为定理,3、上面构造现象完全是有浮力引起的。
,该式中ρ流体大于ρ物,物体上浮,否则下沉。因此上述对盐丘,底劈(穹窿)构造形成的解释是尴尬的!该如何解释这类构造呢?是否可以用浮力解释以上构造现象,下面对浮力的通过引力场理论的求解,可以回答以下问题:1、明确的回答浮力与是否为流体无关;2、浮力仅能称为定理,3、上面构造现象完全是有浮力引起的。

所有大的天体都为球体,即便由细小碎屑组成的小天体小行星Ryugu和Bennu,科学探测发现也为球体[3]。上升、下降、盐丘和底劈(穹窿)都发生在地球上这个同一球体上,上述的陈述告诉我们,它们的形成应遵循同一原理。前面根据万有引力定律,已得出可塑单一密度物质下,均匀球内的球内性质Ⅰ。下面在这些性质下,对浮力的形成做数理上的论证,以解释上述各种现象形成的理论上的根本原因。
2、物质上升与下降的引力场分析
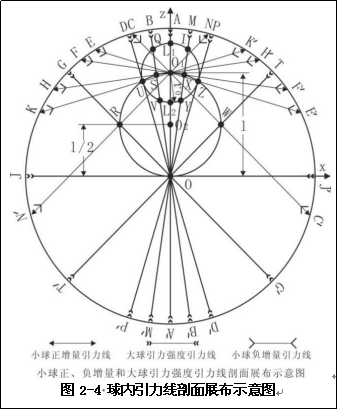
为解觉以上问题,假设图1-9球称为大球,在这大球中存有异于大球密度的小球(见图2-4),此时大球内的引力场将发生改变。按照下面的顺序揭示这种不同,并由此导出小球在大球中相互间的作用力,进而揭示物体上升与下降的上升力、下降力及浮力存在的数理根源。
2.1、大球引力强度和小球增量概念建立
如图2-4示半径为R大球内含有半径为r0的小球,大球的密度为ρ,小球的密度为ρx1或ρx2(ρx1<ρ<ρx2)。小球球心与大球球心的距离为l。假设小球的存在不影响大球形态。
当小球密度假设也为ρ时,此时大球球内,以O为坐标原点时,大球球内引力强度命名为大球引力强度。大球引力强度根据式(1-14)为:
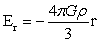 (r≤R)…(2-1)
(r≤R)…(2-1)
式(2-1)成立时,小球密度为ρx2,小球内任意质点小体积ΔV上,少算的质量为-ΔV(ρ-ρx2),这一质量命名为正质量;当小球密度为ρx1,小球内任意质点小体积ΔV上,多算的质量为ΔV(ρ-ρx1)。根据正质量的表达,这一质量为负质量,记为-ΔV(ρ-ρx1)。正、负质量可统一在如下的公式中:
Δm=-ΔV(ρ-ρxi)…(2-2)
小球中多计质量和少计的质量引起的引力场引力强度命名为小球增量,在图2-4中依O1为坐标原点的极坐标系中,由式(2-2)并根据式(1-12)、(1-14)得小球增量如下两表达式。
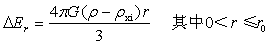 …(2-3)
…(2-3)
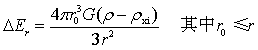 …(2-4)
…(2-4)
上述(2-3)、(2-4)两式中i=1定义为小球正增量,i=2定义为小球负增量。小球正增量方向背离O1,小球负增量方向指向O1。
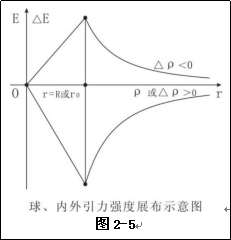
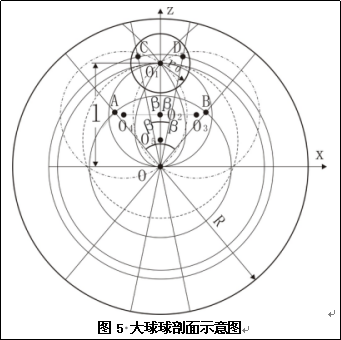
其大球引力强度、小球增量变化见图2-5。式(2-1)和(2-3)为一截距为零的直线函数,式(2-4)为二次反比例函数。式(2-3)和式(2-4)在球面上两函数连续且相等。图2-5中E和△Er分别表示了大球引力强度和小球增量。图2-5横轴的上部表示了小球正增量的小球内、外的展布,下部表示了大球和小球内、外,大球引力强度和小球负增量的展布。
根据式(2-3)和式(2-4)小球增量引力强度线都为直线。小球负增量引力强度线方向背离小球球心,小球正增量引力强度线方向指向小球球心;大球引力强度线方向指向大球球心,它们的展布见图2-4。
2.2、小球平行增量与小球垂直增量概念
图2-4中,大圆内过大圆圆心O的直径以AA'为对称,DD'、PP'与圆O1相切。由图中O1向过O每一直径做图示的垂线,垂足分别为S、U、R、O、W、Z、X。这些点共圆,在图2-4中以O为坐标原点的坐标系下的方程为:
x2+(z-l/2)2=l2/4 …(2-5)
图2-4中人为的划分了两个引力场:大球引力场和小球增量引力场。通过小球增量在图2-4中每一经过O的大球线段投影,就可知道大球内引力场展布情态。小球增量在大球内的任意大球直径上,存在两个分量:①平行于大球直径的纵向分量--小球平行增量;②垂直与大球直径的横向分量--小球垂直增量。由于小球增量分正负,所以小球正增量在大球内的任意大球直径上有:小球正平行增量和小球正垂直增量;同理小球负增量有小球负平行增量和小球负垂直增量。为方便叙述问题,假设如下参数:R=50cm,l=35cm,r0=10cm,ρ=3kg/cm3,ρx1=1kg/cm3,ρx2=5kg/cm3。
2.3、小球平行增量展布特征
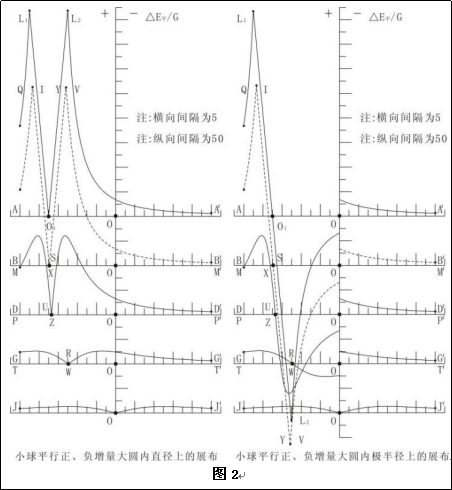
小球平行增量在大球内有两种展布形态:一种是沿图2-4过O图示直径的展布;二是在大球任意半径的展布。下面根据上面假设的数据给出小球平行增量展布图。而以上两种展布计算相当繁琐,与要解决的问题作用不大,所以下面仅给出计算后的展布示意图。
2.3.1、小球平行增量任意直径上展布特征
图2-6是图2-4中小球的小球平行增量,在图2-5中过大球心O的直径上的投影(后面附录了图2-6的形成过程)。
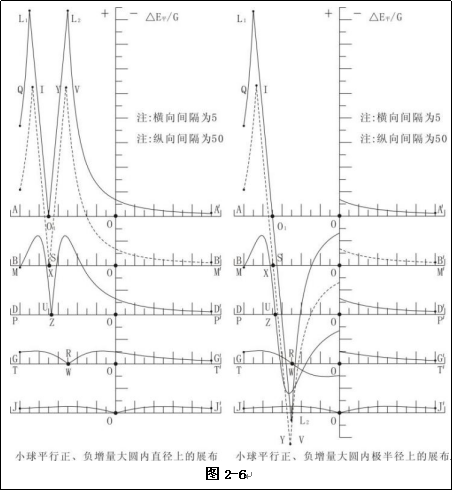
图2-6左侧标识了小球平行增量沿大球任意直径的变化,右侧图标识了与大球引力强度的方向关系。图2-6每一直径上凡过圆O2的值均为零,其外部小球平行正增量均与大球引力强度反向,内部则与大球引力强度同向。
2.3.2、小球平行增量任意大球半径上的展布特征
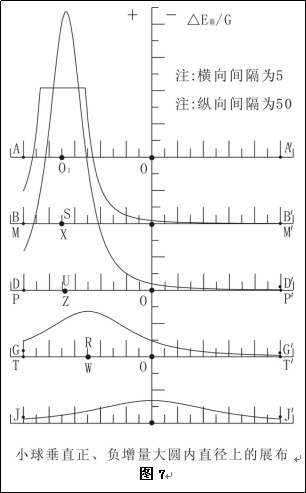
图2-7是图2-5中小球的小球平行增量,在图2-4中大球内距球心O为r的半径上的投影(后面附录了图2-7的形成过程)。
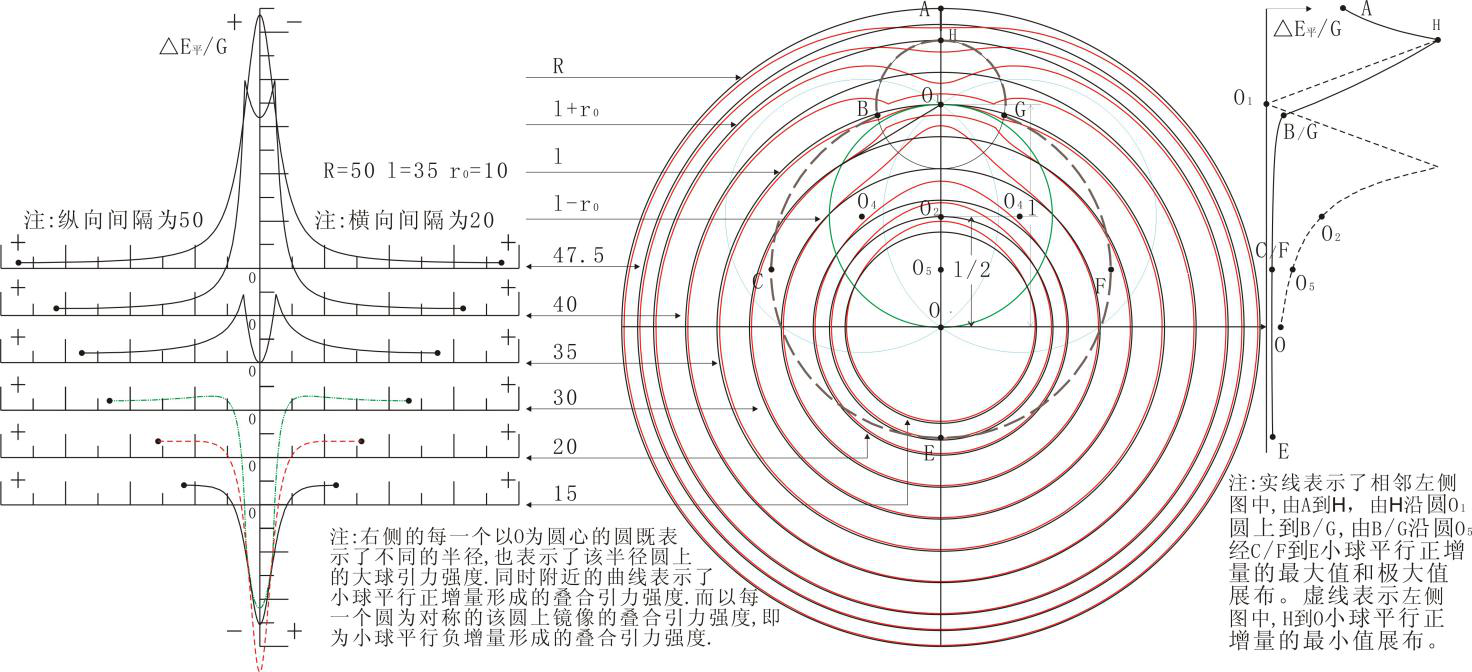
图2-7 小球平行正增量球内同半径球面上展布剖面示意图
在图2-7圆O2的圆上,小球平行正增量为零,然后在圆O2的过圆内图示的不同黑色的大球半径上,小球平行正增量与大球引力强度同向,外部小球平行正增量与大球引力强度则相反。小球平行正增量在圆O2的圆内部:①半径在小于l-r0的半径的大球内圆上,由O2的两边圆上对称向中心增大,到AO上取得最大值,方向指向大球球心;②半径在大于l-r0小于l的大球内圆上,由O2的两边圆上对称增大,到O1的圆上达到最大,方向指向大球球心。小球平行正增量在圆O2的外部:③半径为l到l+r0的大球内圆上,由两侧小球平行正增量对称增大,到圆O1的圆上达到最大,由圆O1圆的两边到对称轴AO,将不断变小直至最小,方向背离大球球心;④半径大于l+r0的大球内圆上,由两侧小球平行正增量对称增大,到AO的上达到最大,方向背离大球球心。对于小球平行负增量则与之相反。
通过以上发现,图2-4或图2-7圆O2内,小球平行正增量与大球引力强度叠加后,绝对值增大;外部小球平行负增量与大球引力强度叠加后,绝对值减小。前者命名为增量区,以“+”表示,后者命名为减量区,以“-”表示,见图2-8左侧图。小球平行负增量与上述所有结论与上相反,见图2-8右侧图。从图2-8可以看到:左侧图“负阴抱阳”,右侧图“负阳抱阴”。所以小球平行正增量在大球内的展布称负阴抱阳性;小球平行负增量在大球内的展布称负阳抱阴性。在这种负阴抱阳或负阳抱阴区域中以小球周边的小球增量变化最为剧烈。
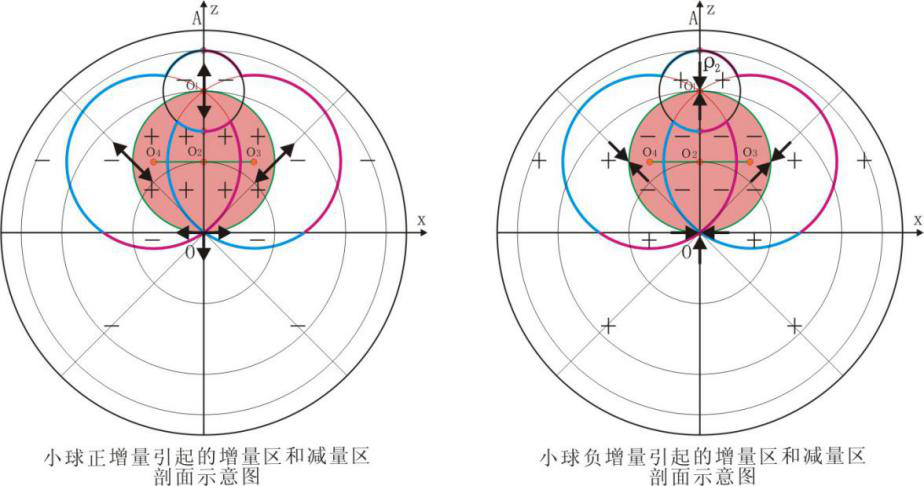
图2-8
对于图2-7、2-8中虚线圆,蓝线、粉红圆弧具体意义,与后面的关系不大,故不再交代具体物理意义,但附录中有详细交代。
2.4、大球内小球垂直增量展布特征
小球垂直增量在大球内有两种展布形态:一种是沿图2-4过O图示直径的展布;二是在大球任意半径的展布。下面根据上面假设的数据给出小球垂直增量展布图。而以上两种展布计算相当繁琐,与要解决的问题作用不大,所以下面仅给出计算后的展布示意图。
2.4.1、小球垂直增量任意直径上展布
图2-9是图2-4中小球的小球垂直增量,在图2-4中过大球心O的直径上的投影。(后面附录了图2-9的形成过程)。
从图2-9中可以看出,图2-4中AA'小球垂直增量全为零;BB'和MM'过小球,过小球部分不变,其它则如图2-9所示的变化,但极值都在O2的圆上。小球垂直增量以AO为为对称,方向小球垂直正增量相背,小球垂直负增量相对。以大球内的任意半径为例,由OA两侧沿该圆对称变动位置,小球垂直正增量的方向不断改变,到OA变为两侧相对;小球垂直负增量则与之相反。
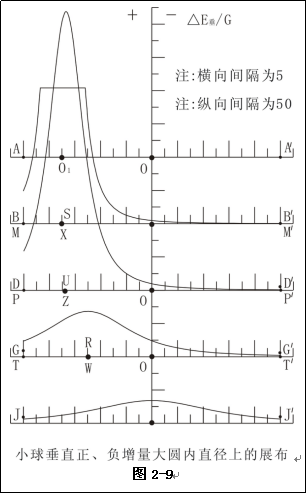
2.4.2、小球垂直增量任意大球半径上的展布特征
图2-10是图2-4中小球的小球垂直增量,在图2-4中大球内距球心O为r的半径上的投影。(后面附录了图2-10的形成过程)。
在图2-10中可以发现图2-4大球内任意一个半径的圆上,有两个极值,这两个极值与另外相邻半径圆上的连线,为图上ABCDOEFGH甲壳虫状。其极值变化见右上标注的图示。
大球内小球垂直增量任意半径上以z轴为对称,变化最大的区域图2-10中如带角甲壳虫区域附近。所有点的小球垂直正增量以z轴对称,上半圆呈一定角度的镜像背离,下半圆小球垂直正增量呈一定角度的镜像相对,见图2-11左侧图的展布。对于小球垂直负增量,则与之相反,见图2-11右侧图的展布。
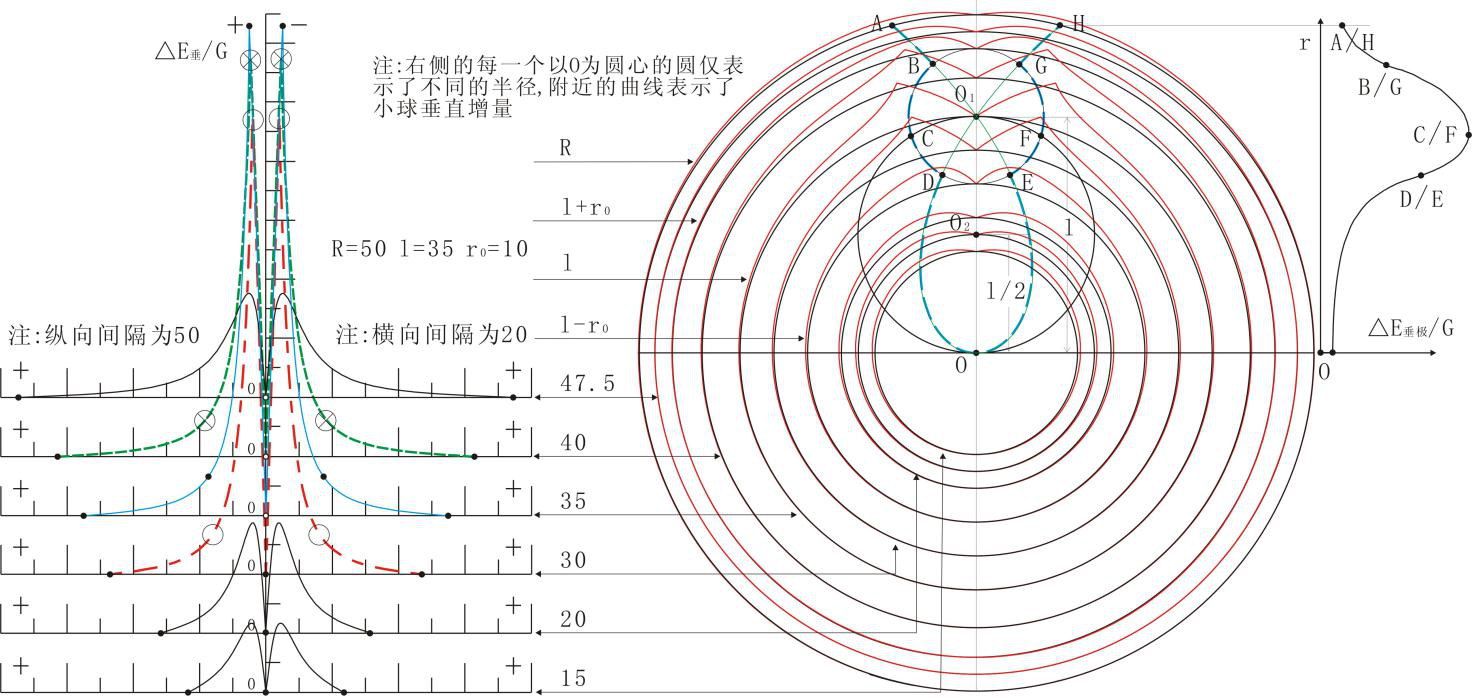
图2-10 小球垂直正、负增量同半径上的剖面展布示意图
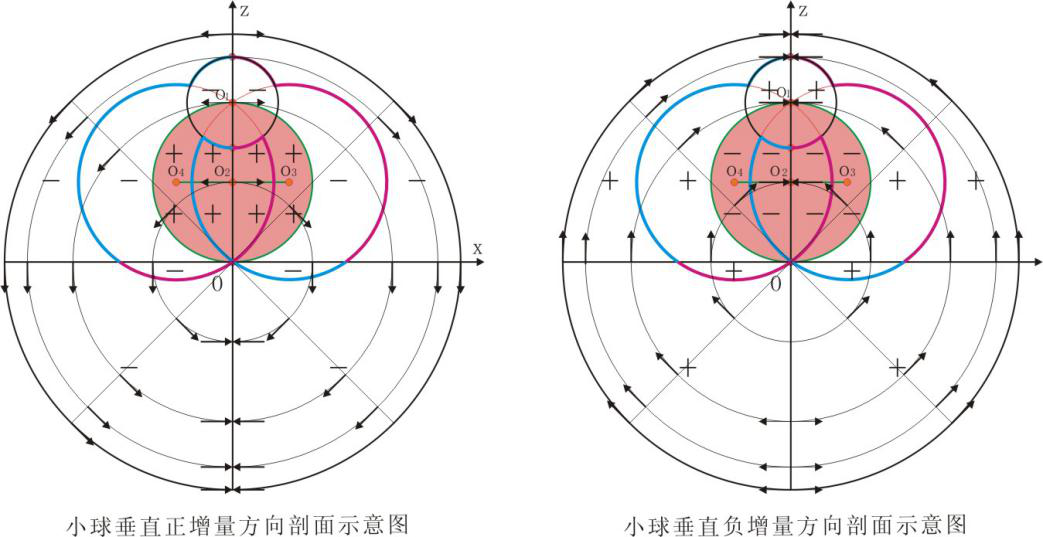
图2-11
3、小球上升、下降的成因分析
通过上面的小球增量在大球内的展布分析,小球增量在大球内展布具有一定规律性。这些规律性展布结合球内性质Ⅰ,可得出大球内所有质点均处于不稳定、不平衡的状态,因而大球内所有质点具有强度不同的态势和运动动力。这种全球性运动的态势会造成什么规律性的运动,下面做分析。
3.1、大球内小球上升成因分析
小球正增量两个分量:小球平行正增量和小球垂直正增量。下面依据这两个分量分析大球内小于大球密度的物质的上升的成因。
3.1.1、小球平行增量引起的小球上升成因
小球平行正增量在图2-6、7圆O2内与大球引力强度同向,外部反向,因而图2-7圆O2内,压力、引力位较之大球内稳定时压力、引力位增大,而外部与之相反。大球内同半径圆上,压力、引力位增大与减小形态,与该圆小球平行正增量形态相同。
下面以压力参数分析,以大球引力强度推导而来的压力为基态,小球平行正增量在图2-7圆O2内的引起的压力是增大的,以外的区域是减小的。在圆O2内在小球的底部,沿z轴小球因小球平行正增量获得最大合压力,由此向两侧合压力逐渐减小。压力大的地方物质就会向压力小的地方释放,因而小球就获得向上的力;在小球的外部沿z轴,小球上部因小球平行正增量获得最大的合压力减小,由此向两侧减小的合压力逐渐减小。这样以来小球的压力的上减下增就使得小球具有了远离大球球心的力。对于引力位为参数,也可有以上类似的分析,不再赘述。这就是小球上升原因之一。
3.1.2、小球垂直正增量助力的小球上升
图2-10右侧图和图2-11左侧图中小球垂直正增量,使得小球周边有了对称的背向横向压力,这种压力沿图2-11左侧图中小球垂直正增量标注的方向。在大球上半球,横向压力由最初的相对背离,不断改变方向到大球的下半部形成相对。在上半球的横向上压力使得上半球在横向上对称减压,而每一对称的横向减压又对其后部形成增压积累,这种积累形成沿图2-11左侧图中小球垂直正增量标注的方向后传。上半球的横向压力对称减小,而以小球周边为最。上半球的横向压力对称减小及压力积累为小球远离球心O,提供便利。下半球小球垂直增量的横向压力,使得下半球压力横向压力增大,而每一横向对称增压又对后部形成压力积累,以及上半球传来压力也积累于此,到z轴形成所有横向压力的相对。下半球的所有横向压力对上半球尤其圆O2的方向形成压力传递支撑,这种支撑又传递到小球的底部,为小球远离球心O提供传递支撑力。这是小球上升原因之二。
3.2、大球内小球上升成因进一步归纳
通过上面的分析,可以得到:小球平行正增量使得阳区增压,阴区减压,一增一减使得小球具有了远离大球球心的纵向动力,增压区和减压区变化尤以小球周边为甚。小球垂直正增量使得上半球形成对称横向减压及横向对称向后传递压力积累,而小球垂直正增量横向减压以小球周边为甚,为小球上升创造横向方便;小球垂直正增量使得下半球形成横向对称增压,并接受后部及上半球传递来的压力积累,到z轴为甚;下半球的增压及增压积累上传到增压区方向,进而促成小球上升的另一上升动力。以上两种动力便是小密度物上升的动力,这两种力具有全球性。为方便见,称上述过程为小密度物上升原理。
小球在大球中的上升,大球内的引力场将不断地改变,所以大球内所有质点都有不同位置运动,这一运动具有全球性。而发生运动的最为剧烈的地方在小球周边,因小球上升小球顶部的物质不断向周边运动,而小球底部将出现物质亏损,因而小球顶部的物质俯冲予以补充,同时质心随小球的上升不断地向大球球心靠近。小球上升到出露球面建立平衡引力场后,停止上升,这时平衡引力场后面会述。在小球上浮过程中负阴抱阳不断改变,阳的部分不断扩大,阴的部分不断缩小。由此可以看出小密度物在大密度物中上升,正是上述原因产生的。
从上面的分析可以可看到小密度的小球,栖居于大密度的大球内,将受到来自大球内所有质点的作用力,这种作用力使得小球具有了上升力,下面将通过数学手段计算这一力。
3.3、大球内小球下降成因分析
分析完小球正增量导致的小球上升,由于小球负增量与小球正增量仅是方向的相反,所以无须再分析小球负增量形成小球下降的力学原因,只需把上述过程倒过来看就行了。小球的小球正增量,存在小密度物上升原理,小球的小球负增量,当然也存在小密度物下降原理,同样因与小球负增量与小球正增量方向的相反,也不在赘述。
3.4、大球半径无限大时小球增量的局部投影
图2-4大球半径如地球半径大小,而小球大小不变,如篮球大小,居大球内,距大球表面距离极小,见图2-4(R→∝)。根据上述条件,图2-4中,切线DO与AO(或PO与AO)的夹角为α=arcsin(r0/l),由于l与R几近相等,所以夹角α也趋于零。所以图2-4的局部图2-4(R→∝),经过O1的不同半径大球圆的局部可以看作平行线;经过O1的大球引力强度线的局部也可以看作平行。
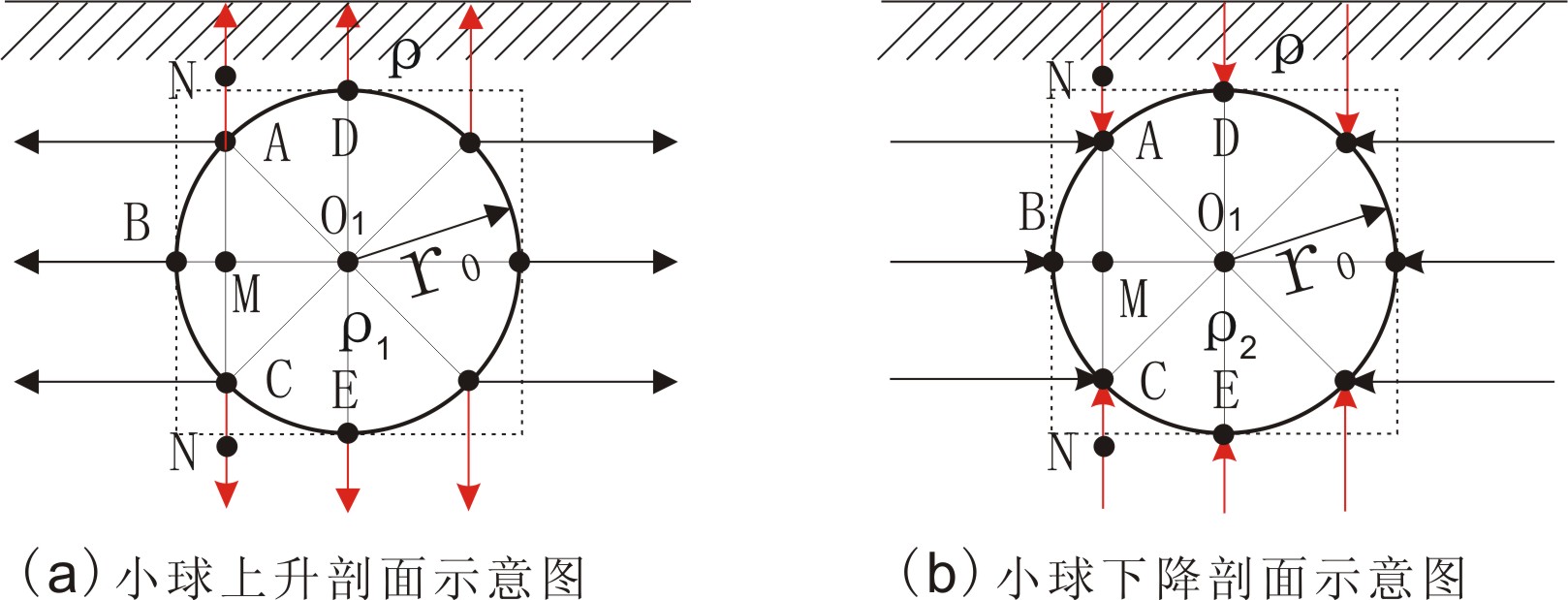
图2-4(R→∝)
因此,图2-4(R→∝)红色的平行线是小球平行增量,黑色线是小球垂直增量。这样一来,对理解小球的上升与下降更为直观。对于旋转球台,当旋转角也与小球一样,就成了图示的虚线表示的圆柱。
4、小球上升、下降力的计算
上面分析出了小球上升和下降的原因,但小球在大球内上升和下降的力是多少?下面计算之。下面就计算异密度小球与包围的大球物质间的作用力。为进一步证明上升力与下降力的合理性,用不同的方法来计算上升力与下降力。
图2-12(a)大球中含有异于大球密度的小球,大球内存在两引力场:大球引力场和小球增量引力场。图2-12中,线段AD过O1,与z轴的夹角为α。AD线段的端点A、D在半径为R的球面上,该线段与半径为r0的小球球面的交点为B、C。B点在xy平面上的投影点和O1的连线,该连线与x轴正向夹角为θ,如图2-12a中所示。
4.1、异密度小球与小球外部大球内间相互作用力计算
在第一部分中,计算了划定区域于均匀球内的稳定平衡力,这一力因稳定平衡支持力的存在并不做功。但划定区域密度改变后,上一部分通过引力场的分析,划定区域异密度小球要么上升,要么下降。图2-12中小球即为密度改变区域,密度为ρxi(i=1,ρx1<ρ;i=2,ρx2>ρ)。这时的小球与前面划定区域相比,仅是小球密度改变,其它条件没有改变,因此根据对稳定平衡力的计算方法,此时小球与大球内小球外部的作用力为:
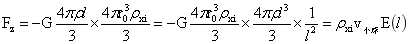 …(2-6)
…(2-6)
小球密度i=1,ρx1<ρ时,式(2-6)的绝对值,小于式(1-35)稳定平衡力绝对值;小球密度i=2,ρx2>ρ时,式(2-6)的绝对值,大于式(1-35)稳定平衡力绝对值。根据本部分第2节异密度小球存在于大球,球内的引力场较之单一密度下引力场发生改变,并由此分析出小球具有上升和下降的可能,所以式(2-6)所表达的力是一种不稳定力。
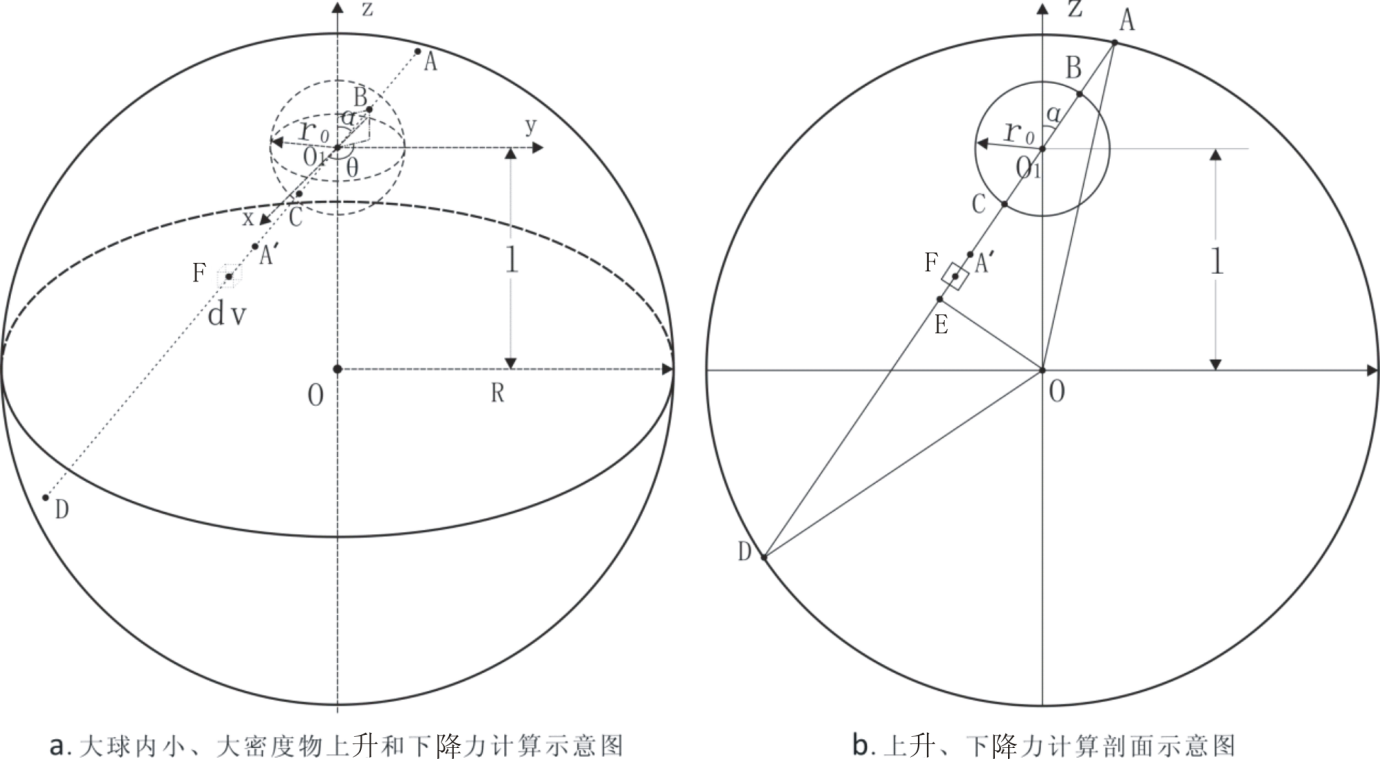
图2-12
对于图(2-12)小球位置换为旋转球台,旋转球台的不稳定力为:
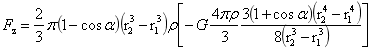 …(2-7)
…(2-7)
式(2-7)中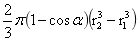 为旋转球台的体积,
为旋转球台的体积,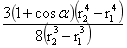 为均匀旋转球台的质心距O的距离r,r1、r2为旋转球体内外半径。
为均匀旋转球台的质心距O的距离r,r1、r2为旋转球体内外半径。
4.2、上升和下降力的分析计算
式(2-6)的不稳定力的存在,存在于大球内异密度的小球具有上升与下降的可能,上升力与下降力是多少呢?在第一章中得出稳定平衡力的同时,也分析出稳定平衡支撑力。稳定平衡支撑力作用方向背离大球球心,而不稳定力的作用方向指向球心,两力的作用点都在小球球心,因此稳定平衡支撑力与不稳定力的合力即为上升力或下降力,因此式(1-36)与式(2-6)相加为:
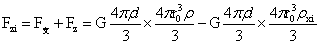
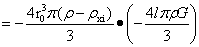
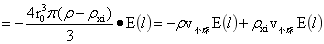 …(2-8)
…(2-8)
上式中i=1,ρx1<ρ,Fz1>0,图2-12中小球上升,此时的力称为上升力;i=2,ρx1>ρ,Fz2<0,图2-16中小球下降,此时的力称为下降力。但式(2-8)还可以用以下其它方法求出,下面就介绍这方法。
同样对于图2-12小球位置换为旋转球台也有类似(2-8)的表达式为:
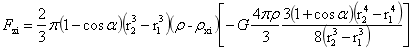
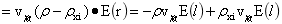 …(2-9)
…(2-9)
4.3、上升力和下降力的直接计算
图2-12位于大球中,小球的质量增量为: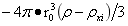 。这一质量与大球内图2-12b中任意F的质点质量为ρdv的相互作用力为:
。这一质量与大球内图2-12b中任意F的质点质量为ρdv的相互作用力为:
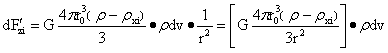 …(2-10)
…(2-10)
由式(2-10)可以发现左侧为为万有引力定律的表达形式,经变形右侧中括号部分为小球增量,于是右侧部分就表达了以O1坐标原点,小球增量场下,图2-12b中E点质量为ρdv的受力。
用第一部分稳定平衡力的计算方法,对(2-10)积分得:
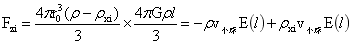 …(2-11)
…(2-11)
式(2-11)即是在小球增量场下直接得出,也是小球的质量增量与大球内所有质点合力万有引力的得出。同时该式与式(2-8)相同,说明4.2部分上升力和下降力的计算是正确的。
对于图2-12小球的位置换为旋转球台,旋转球台的密度同小球的假设一样,其旋转球台的上升力或下降力的计算表达式为式(2-9)。
通过上面小球、旋转球台上升力或下降力讨论,二力仅与密度、体积和物体的质心引力强度有关,且由上二力得出稳定平衡支撑力就是时下称的浮力。
5、成果总结
从上面2至4部分的分析得出了许多成果结论,这些成果结论是大球内部所有质点运动的理论根据,成果总结如下:
1、等时共同作用定理 浸入大球异于大球密度的小球或旋转球台等,改变均匀球内引力场,已分析出平行正(负)增量特征和小球垂直正(负)增量特征。这些特征即表明球内引力场展布特征,也表明所有质点处于不稳定状态。无论小球或旋转球台等是远离大球球心,还是接近大球球心,所有质点共同参与且等时,为方便后面的陈述,将这一特征命名为等时共同作用定理。其内容如下:栖于大球中的异于所栖位置大球密度的异密度物质,大球内所有质点间,不以物质的相态而存在不稳定的相互作用力,所有质点运动具有等时性。
2、上升力定理 小密度物上浮是在平行正增量性质和垂直正增量性质进一步分析得出的。这一原理揭示小球、旋转球台等密度小于大球时,存在于大球内的小球、旋转球台等具有受大球排斥受力特征,将排斥力这一特征命名为上升力定理,其内容如下:栖于大球中的小密度物,小密度物多计质量受到不以物质的相态而存在的大球的排斥力,排斥力的大小为多计质量与大球在小密度物质心处大球引力场强度的乘积,即为: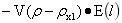 ,其中ρ>ρx1。
,其中ρ>ρx1。
3、下将力定理 大密度物下沉原理是在平行负增量性质和垂直负增量性质进一步分析得出的。这一原理揭示大密度物大于大球密度时,存在于大球内的大密度物具有受大球吸引受力特征,将吸引力这一特征命名为下降力定理,其内容如下:栖于大球中的大密度小球,大密度物少计质量受到不以物质的相态而存在的大球的吸引力,吸引力的的大小为大密度物少计质量与大球在大密度物心处大球引力场强度的乘积,即为: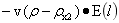 ,其中ρ<ρx2。
,其中ρ<ρx2。
4、浮力定理 上浮力定理、下沉力定理中均有两项组成。一项为稳定平衡支撑力,该力为小球或旋转球台等排开大球物质质量的受力--稳定平衡力的反作用力,为小球排开大球物质质量与大球在小球或旋转球台等质心处大球引力场强度的乘积的负值;另一项为无论小球或旋转球台等密度是大是小,小球或旋转球台等在大球内大球引力场强度下的受力--非稳定力,其大小为:小球或旋转球台等质量与大球在小球或旋转球台等质心处大球引力场强度的乘积。通过这两力上面的分析,与小球或旋转球台等栖居的物质和自身物质是什么相态不存在关联。由此而知稳定平衡支撑力就是时下称的浮力,为延续传统仍将稳定平衡支撑力称为浮力,因此有必要对浮力给出下面的定义:栖于大球中的异密度小球受到大球不以物质的相态而存在,具有恢复小球所居位置再平衡大球的稳定平衡支撑力的作用,该力等于该异密度物排开大球物质受到的负引力,方向背向大球球心,数学表达式为: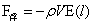 ,
,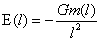 。
。
时称的浮力定律含义可通过旋转球台为例导出。式(2-9)中旋转球台的体积为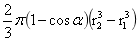 ,当球的半径足够大,比如地球,旋转球台位于球的表面附近时
,当球的半径足够大,比如地球,旋转球台位于球的表面附近时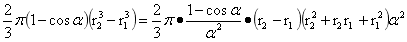 ,当旋转球台旋转角几近于零时,(1-cosα)/α2≈1/2;当旋转球台旋转角几近于零,r1,r2几近相等,旋转球台顶底面几近相等几近为圆平面,设这平面半径为r,(r22+r2r1+r12)α2≈3r2;设h=r2-r1,于是
,当旋转球台旋转角几近于零时,(1-cosα)/α2≈1/2;当旋转球台旋转角几近于零,r1,r2几近相等,旋转球台顶底面几近相等几近为圆平面,设这平面半径为r,(r22+r2r1+r12)α2≈3r2;设h=r2-r1,于是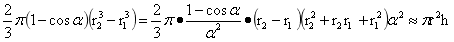 。旋转球台的质心在3(1+cosα)(r24-r14)/[8(r23-r13)]≈R。于是式(2-9)就变为F≈πr2hρ(-4πGρR/3)=hsρE(R)。对于如地球般的球,E(R)在球表面附近极小范围虽有变化,但变化几乎可以忽略,可视为定值,地球的重力加速度在地球表面为几十米范围可视为不变可为其佐证,这时就得出了时下称得浮力定律数学表达式。当圆柱顶底面距球面分别为H1和H2,前者大于后者,于是F≈ShρE(R)=[H1ρE(R)-H2ρE(R)]S,这时就给出了浮力的压力差的成因解释。如果上面的讨论再结合图2-4(R→∝)所表示的引力场,对于理解浮力形成于引力场更为直观。
。旋转球台的质心在3(1+cosα)(r24-r14)/[8(r23-r13)]≈R。于是式(2-9)就变为F≈πr2hρ(-4πGρR/3)=hsρE(R)。对于如地球般的球,E(R)在球表面附近极小范围虽有变化,但变化几乎可以忽略,可视为定值,地球的重力加速度在地球表面为几十米范围可视为不变可为其佐证,这时就得出了时下称得浮力定律数学表达式。当圆柱顶底面距球面分别为H1和H2,前者大于后者,于是F≈ShρE(R)=[H1ρE(R)-H2ρE(R)]S,这时就给出了浮力的压力差的成因解释。如果上面的讨论再结合图2-4(R→∝)所表示的引力场,对于理解浮力形成于引力场更为直观。
流体中的物体受到的浮力,被华夏先贤发现系统总结两千多年以来,西方学者“承袭”后称为阿基米德定律(或浮力定律或阿基米德原理)。在没有从最基本的力学原理万有引力定律中导出上述关系前,称这一反复实验纠错得出的成果为定律无疑是正确的,但现在从最基本的万有定律中推求出浮力,再称定律无疑是不恰当的,因此建议将上述给出的浮力定义称为浮力定理。
6、异密度物引起的动力学
从小球增量的大球内展布及讨论看,大球球内所有质点已不再遵守球内性质Ⅰ,即所有质点均处于不稳定不平衡状态;对于小球换为旋转球台等,上述规律同样成立,不再单独讨论。这种不平衡不稳定状态,将在合引力强度下受力,受力就将产生质点运动。于是根据不同的力学参数可出现球内不同的动力学现象。
6.1、引力强度梯度动力学或重力动力学
以引力强度为参数,根据图2-7、2-8,2-10、2-11,大球内同球面上任意点上引力强度值不再相等,横向上引力强度梯度不再为零,纵向上引力强度梯度不再相等。这两点不同,根据球内性质Ⅰ为求的质点的平衡和稳定,为使同球面上任意点引力强度相同,质点引力强度大的地方将向引力强度小的地方运动,如果对这参数引起的动力现象命名可称为引力强度梯度动力学或重力动力学。
6.2、引力位梯度动力学或势能动力学
以引力位为参数,根据图2-7、2-8,2-10、2-11,同球面上任意点上引力位值不再相等,横向上引力位梯度不再为零,纵向上引力位梯度不再相等,这两点不同,根据球内性质Ⅰ为求的质点的平衡和稳定,质点引力位大的地方将向引力位小的地方运动,如果对这参数引起的动力现象命名可称可称为引力位梯度动力学或势能动力学。
6.3、压力梯度动力学
以压力为参数,根据图2-7、2-8,2-10、2-11,同球面上任意点上压力值不再相等,横向上压力梯度不再为零,纵向上压力梯度不再相等,这两点不同,根据球内性质Ⅰ为求的质点的平衡和稳定,质点压力大的地方将向压力小的地方运动,如果对这参数引起的动力现象命名可称可称为压力动力学或压力梯度动力学。
6.4、质心动力学
从大球的质心看,小球密度小于大球时,质心位于大球球心之下,否则位于大球球心之上。根据前面对小球受力,无论小球上升还是下降,质心都向大球球心运动。根据这一运动,可命名这一运动为质心动力学。
6.5、拱形桥支撑力动力学
从力的角度看,小球密度无论大与小,根据球内性质Ⅰ,大球内质点稳定平衡时横向引力强度为零,但小球的加入,大球内任意点都存在不为零的横向引力强度。因此大球内任意球面上的质点都存在横向力,以小球周边变化剧烈明显,其它区域则有些微不足道,从剖面上看力象拱形桥的受力作用,因此又可得出拱形桥支撑力动力学等。
6.6、应力积累动力学或黏度动力学
如果大球的物质黏度限制小球运动,小球的存在必然造成大球内任意质点上不稳定性应力积累,如果给这一现象取一动力学名称,可命名为应力积累动力学。但应力积累的产生与大球的物质黏度有关,可见黏度也是一种动力作用,因此应力积累动力学又可称黏度动力学。
7、系统力学动力学形成粗论
上面根据不同的力学参数,因异密度物的存在给出不同的动力学名称,如果结合其它物质特性还可给出新的动力学名称。这些后面陆续根据需要在给出。但需要指出的是从上面提到的动力学名称看,每一动力学都具有全球性和等时性,然核心问题还是要归结到物质增量及球内性质和上升力、下降力上来,但这一切又与大球内引力强度有关,因此在此强调重力动力学为所有动力学中的核心动力学。但这里所强调的重力动力学,与马杏垣先生是有区别的,该处的重力动力学是以均匀球内性质为内涵下重力动力学。
然而上述动力学,在过往的地球动力学的研究中也可见到其身影,下面就一些学者的研究做一罗列。1、马杏垣院士提出重力动力学,将几乎所有构造运动归因于此,而上面提出引力强度梯度动力学或重力动力学至少名字相同。2、崔笃信认为青藏高原的主要动力为印度板块对欧亚板块的碰撞力和与重力势能变化引起偏应力,而上面提出引力位梯度动力学或势能动力学至少提到重力势能。3、胡宝群博士提出地球地压梯度动力学,以解释其他所遇到的地质构造现象动力问题,上面归纳出的压力梯度动力学至少名字相同。4、黄定华提出地核偏心动力学,上面归纳出的压力梯度动力学至少名字相同。5、毛小平博士提出周向应力动力学,并以拱形桥示意,上面归纳出的拱形桥支撑力动力学至少名字相同。6、吴珍汉认为地球构造动力,以应力积累为最,前面提到的应力积累动力学(黏度动力学)可与之相类。
通过上面的讨论,下面根据毛小平博士对地球动力学的研究者和他们的观点的统计进一步谈一些我的看法。
1、Lliboutry提出“脊推力”,并以该力计算了软流圈的绝对速度以及速度和剪切应力。笔者认为脊推力的形成源于洋脊的形成,洋脊的形成源于脊下物质受热,而物质受热引起密度的减小,物质的体积增大。这时一是引起局部区域的压力高于周边,二是减小密度物质具有上升力,从而形成洋脊,进而改变原有的稳定与平衡,洋脊具有了横向的推力。继而使得洋底和洋底下物质向压力或势能低的地方,以层流的方式运动。梁光河博士提出了类似的构造运动硅铝物漂移运移。
2、万天丰以陨石撞击,地幔羽浮力大陆裂解,引起放射性板块运动,碰撞破碎带产生大陆增生等。Rampino以巨大陨石撞击地球,诱发深部地幔物质上涌,板块放射性扩张。在笔者看来陨石撞击地球尤其是大的,撞击点获得巨大动能及物质的积累。显然造成原有的稳定平衡的破坏,出现有限放射性构造是非常自然的事情,背后逻辑是为恢复和再造新的全球性平衡。
3、李德威博士考察青藏高原得出的层流动力学;Royden以青藏地区是大陆汇聚的结果,由于下地壳太弱,上地壳变形与下地幔运动脱节提出层流模型;李杨鉴以水平力和重力同时作用提出大陆层控构造;Klemperer以重力产生横向流动提出层流模型。根据前面浮力形成过程的分析看,硅铝物质在大规模的汇集引起的不平衡,为实现新的平衡横向流动也是自然的事情,学者们提出层流动力学是自然的事情。
上面简单罗列性分析,如果以球内性质Ⅰ判断,均是不错的地球动学成就与成果,是非常值得称赞的。但由于没有恰当的能系统性解释的基础理论予以支撑,全部被称为假说。但有了球内性质Ⅰ以及由引力场的导出浮力定理等,本部分所提及的学者们的可能有夸大性的成果,都是成立的。至于毛小平博士对地球动力学的研究者和他们的观点的统计的其它学者成果,将在下面进一步理论探索后进一步涉及。
目前关于构造运动的同时性,或准同时性,用等时共同作用定理可以给出肯定的答复,这一结论无疑是正确的,因而这一结论不再是无根之木。
综上讨论,笔者认为随着可塑物质为球及物质上升、下降等理论的系统性形成,各种已得的地球动力学成果具有了成立的理论依据。因此目前笔者目前所提出的应用于地球动学的研究的理论,称为地球系统力学动力学。是否正确还望大家批评指导!
8、结语
从上面的分析得到上升力和下降力及浮力并不与物质相态相关联,两力是不同密度物质间分异概念的灵魂、本质所在。对于引言提到的盐丘和石蜡水银实验现象,完全可以直接用上升力和下降力及浮力定理进行解释。低密度的弱刚性岩盐层居于大密度的弱刚性泥岩或泥沙岩中,岩盐层存在浮力或上升力,弱刚性泥岩或泥沙岩难以束缚弱刚性岩盐层浮力,从而导致盐丘形成。
对于太空舱燃烧的蜡烛形态,做如下解释。蜡烛燃烧有以下两方面作用:一是燃烧释放CO2及H2O混合粒子,混合粒子因温度高粒子间距离变大,因而形成低于周边空气的低密度混合气体;二是燃烧释放的热,使得周边空气获得热,空气中粒子间距离增大,密度降低。这些低密度混合气体,在不同力场下将使得燃烧表现不同形态。在地球引力场中,地面燃烧蜡烛,以上这些低密度的混合物从而使加热后的空气具有上浮力而上升,而造成底部出现真空,真空对周边的空气形成吸力,这就为形成对流创造了条件。持续燃烧的蜡烛,对流形成。对流对燃烧的火苗一是从底部提供氧气,二是提供氧气的同时从底部开始对燃烧的火苗形成压力,使得火苗变为图2-3左侧形态。在太空舱中几乎不存在地球重力场值与太空舱中绕地球做匀速圆周运动,其合力强度为零,因此太空舱中的空气自然形成一独立的引力场,这一引力场中心,根据高斯定理,引力强度为零点基本在太空舱几何中心点上。在这独立的引力场中,上述低密度混合气体受到浮力。如果蜡烛居于空气引力强度为零点位置上,任意方向浮力大小相同,从而负压也相同,进而任意方向形成对流大小作用相同,对流对燃烧的火苗的压力也相同,所以蜡烛火苗为图1右侧球形。燃烧蜡烛少偏离引力强度为零点,因独立引力场强度太小,也不会使火苗有肉眼可见的变化。
“天宫课堂”中,宇航员将乒乓球放入玻璃水杯水中,乒乓球没有象在地球球面上浮,据此得出太空舱中水中乒乓球不存在浮力的结论。根据对燃烧蜡烛形态的的分析和本部分浮力的形成的引力场分析,因此“天宫课堂”中讲乒乓球不存在浮力的结论是错误的。
参考文献
[1]昆明地质学校主编 构造地质及地质力学,地质出版社 1979年8月 第60页
[2]池顺良 漫话内波(四)盐丘-两种可流动固态物质交界面上的内波 https://blog.sciencenet.cn/blog-51667-498697.html 科学网博客 2011-10-19
[3]王帅 胡森 小行星Bennu和Ryugu的新发现对小行星起源和演化的新认识(http://www.igg.cas.cn/xwzx/cutting_edge/201905/t20190505_5287635.html) 前沿报道 2019年5月
[4]李务伦 李相通 梁殊林 邵艳宁 物体上浮与下沉原理探讨及诸多地球动力能系统统一的分析 https://blog.sciencenet.cn/blog-3433895-1371221.html 2023年1月9日
[5]李相通 李务伦 梁殊林 邵艳宁 “阿基米德定律”可称为“阿基米德原理”数理初论证(1)--暨初首揭物体浮、沉形成过程的数理成因 https://blog.sciencenet.cn/blog-3433895-1399992.html 2023年8月23日
[6]李务伦 李相通 梁殊林 邵艳宁 首揭均匀介质中物体浮、沉与阿基米德定律存在的数理根源(2) https://blog.sciencenet.cn/blog-3433895-1399996.html 2023-8-23
[7]李务伦 李相通 梁殊林 邵艳宁 大球内具有圈层结构的上浮力、下沉力及浮力的计算(3) https://blog.sciencenet.cn/blog-3433895-1400002.html 2023-8-23
[8]李务伦 李相通 梁殊林 邵艳宁 小球上浮与下沉的后的平衡-圈层的形成及存在的动力过程讨论(4) https://blog.sciencenet.cn/blog-3433895-1402366.html 2023-9-12
[9]李务伦 我为什么进行上浮和下沉力的数理形成的探讨 https://blog.sciencenet.cn/blog-3433895-1412547.html 2023-12-5
[10]李务伦 李相通 梁殊林 邵艳宁 上浮力和下沉力的第二种算法 https://blog.sciencenet.cn/blog-3433895-1414657.html 2023-12-20
[11]李务伦 “天宫课堂”中浮力不存在的实验结论不正确 https://blog.sciencenet.cn/blog-3433895-1417467.html 2024-1-11
[12]李务伦 太空舱燃烧蜡烛火苗形态的为球形的原因 https://blog.sciencenet.cn/blog-3433895-1417963.html 2024-1-15
[12]李务伦 李相通 梁殊林 邵艳宁 万有引力是浮力形成的根源 https://blog.sciencenet.cn/blog-3433895-1437746.html2024-6-11
[13]李务伦 李相通 梁殊林 邵艳宁 浮力形成的万有引力定律又再计算再解释 https://blog.sciencenet.cn/blog-3433895-1467553.html 2025-1-6
[14]李务伦 浮力的“压力差”成因解释是否不妥 https://blog.sciencenet.cn/blog-3433895-1478450.html 2025-3-20
[15]李务伦 时称的浮力可以以压强、压力概念为基础推导出来--暨浮力不应再称定律或原理 https://blog.sciencenet.cn/blog-3433895-1482785.html 2025-4-21
附录一 浮力形成图形成分析1、小球正增量在大球内计算与展布
下面是在前面第2部分2.1,2.2部分基础上叙述。
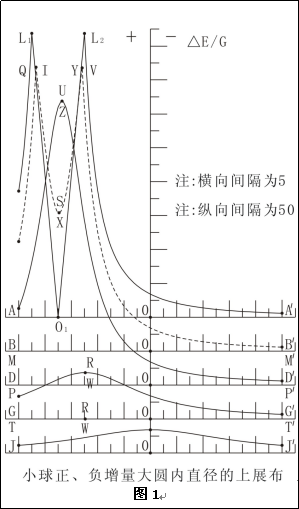
图2-4中沿任意过O的直径上小球增量,先设定坐标系。根据对称性,以图中GG'为例,R为原点,GG'与AO的最小夹角设为α(0≤α≤π/2),OG'向为正向,距离原点R的距离为X。于是任意经O的直径,不含圆O1圆内部分的小球正增量计算公式为:
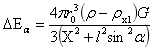 …(1)
…(1)
(1)式为一初等函数,在原点R上可以分析出有极大值,由此点向两侧非线性减小。而与这一直径上小球平行正增量曲线相似的还有直径DD'、PP'、TT'、JJ'。根据假定的密度参数,以上各直径小球正增量变化见图1。小球正增量和小球负增量仅相差一个符号,所以在图1中,正号为小球正增量,负号为小球负增量,小球增量值均没含万有引力常数,以ΔE/G代之,下同。
图2-4中,过圆O1的的大圆直径,以BB'为例,S为原点,BB'与AO的最小夹角也设为α,取值范围[0≤α≤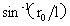 ],以SB'为正向,圆O1内上的小球正增量计算公式为:
],以SB'为正向,圆O1内上的小球正增量计算公式为:
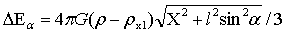 …(2)
…(2)
上式中,x的取值范围[-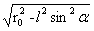 ,
,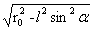 ]。上式在S点上取得极小值,由此向两侧非线性增大到圆O1的圆上取得最大值。根据图2-5这两最大值与式(1)在此处的值相等,由此向上或向下非线性减小。AA'、MM'、BB'上和这一变化相似,见图1。
]。上式在S点上取得极小值,由此向两侧非线性增大到圆O1的圆上取得最大值。根据图2-5这两最大值与式(1)在此处的值相等,由此向上或向下非线性减小。AA'、MM'、BB'上和这一变化相似,见图1。
2、大球内小球平行正增量计算及展布
小球平行正增量计算及展布分两种情况叙述。一是大球内沿任意大球直径上的计算及展布;二是大球内同一半径上计算及展布。
2.1、大球内任意直径小球平行正增量上的计算及展布
计算小球平行(垂直)正增量先设定计算坐标系。以图2-4中GG'为例,原点为R,两侧均为正向,两侧点距R的距离都设为X。GG'与AO的最小夹角设为α,α变化范围0≤α≤π/2。于是图2-4中任意过O的直径上,不含圆O1圆内部分的小球平行正增量为:
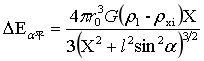 …(3)
…(3)
求上式一阶导数得:
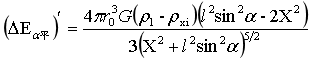 …(4)
…(4)
式(4)等于零有:
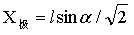 …(5)
…(5)
当X=X极-,式(4)大于零,当X=X极+,式(4)小于零,因此X=X极时有极大值。由此极大值向两侧非线性减小,在X=0时式(3)为零。所以GG'上小球平行正增量变化,见图2左侧图中GG',图2-4中DD'、PP'、TT'、JJ'与之相似,具体变化见图2左侧。
图2-4中任意过O直径上极大值有什么规律呢?以图2-4中GG'上极大值为例,以O为坐标原点的坐标系中,根据式(5)和R点,于是极大值坐标为:
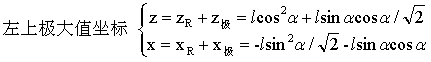 ……(6)
……(6)
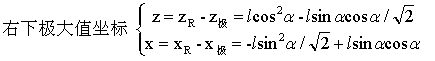 ……(7)
……(7)
由于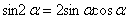 ,
,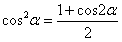 和
和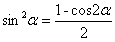 ,解式(6)和(7)分别得如下与角α无关的对应的平面方程:
,解式(6)和(7)分别得如下与角α无关的对应的平面方程:
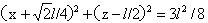 …(8)
…(8)
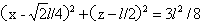 …(9)
…(9)
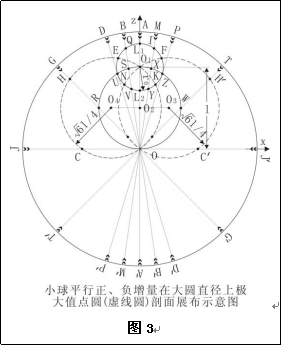
上述二式见图3中圆心为O3、O4虚线圆。在图3中,圆O4与圆O1相交点为E和K,圆O3与圆O1相交点为F和N。可以证明E、N、O和F、K、O三点各共一条直线。设EO或FO与AO夹角α交,由于E或F点是极大值的位置,这时的X值为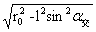 ,于是有如下的等式:
,于是有如下的等式:
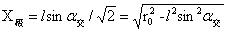 …(10)
…(10)
解(10)得:
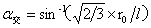 ……(11)
……(11)
图2-4中,任意经圆O1,且过O的直径上,α变化范围为0≤α≤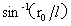 ,坐标系设定同上。圆O1圆内部分小球平行正增量计算式为:
,坐标系设定同上。圆O1圆内部分小球平行正增量计算式为:
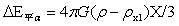 …(12)
…(12)
式(12)为一线性函数,X=0,式(12)等于零,到圆O1的圆上得最大值。图3中,任意直径与AO夹角小于α交,式(3)数学意义上极大值在圆O1的圆内,否则在圆O1的圆外;等于α交时在圆O1上。因此α小于α交时,式(12)在圆O1圆上得最大值,并与(3)式最大值相等。这时小球平行正增量在图2-4直径如BB'、MM'和AA'上的展布,见图2左侧图中BB'、MM'、AA'。
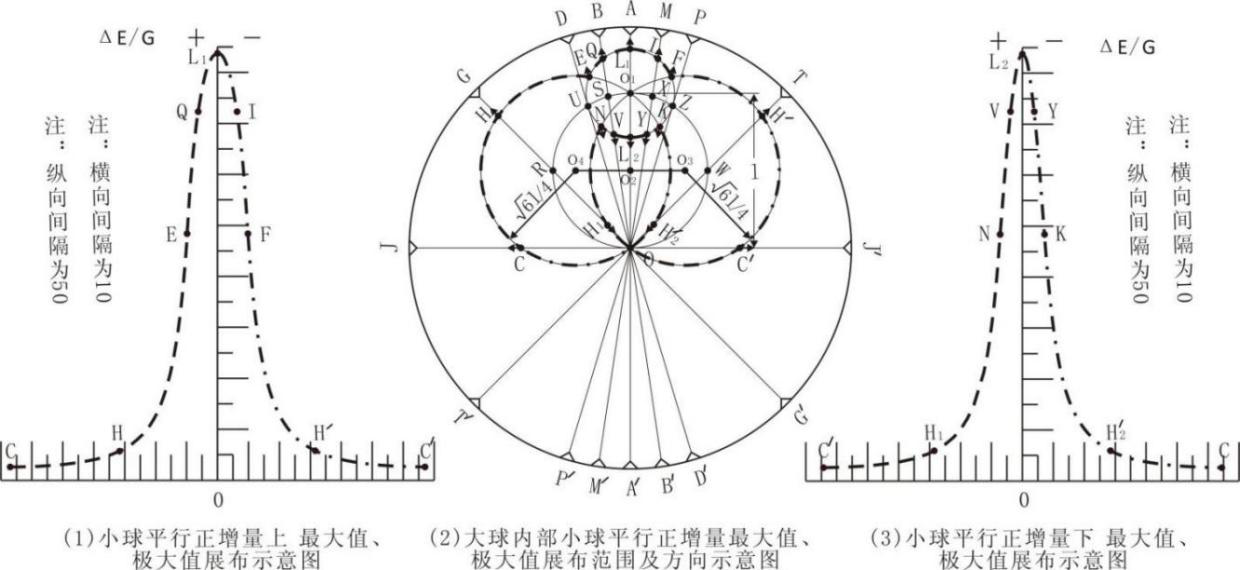
图4
图2中大圆内直径上小球平行正增量,以小球平行正增量方向展布到大球极坐标上,将呈图2右侧展布。图2右侧大球极坐标上,极坐标上部小球平行正增量与大球引力强度方向反向;极坐标下部小球平行正增量与大球引力强度方向同向,位于圆O2的圆内。在圆O2的圆上小球平行正增量全部为零;最大值和极大值的变化值及方向和展布见图4。
2.2、大球内任意半径上小球平行正增量的计算及展布
上面分析了大球内任意直径上小球平行正增量的展布特征,下面分析小球平行增量同半径上球面上展布特征。在分析前先对计算坐标做如下设定:图5中大圆内,半径r为的圆与z轴的上交点为原点,以z轴为对称两侧对称点分别与O连线,该连线与z轴的最小夹角设为β,0≤β≤π。下面分任意半径r过圆O1和不过圆O1两部分讨论小球平行正增量的展布。
Ⅰ、图2-4中大圆内,以O为圆心的任意半径为r圆上,不含经圆O1圆内部分的小球平行正增量为:
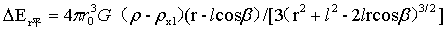 …(13)
…(13)
对上式中β求一阶导数得:
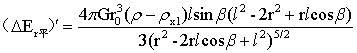 …(14)
…(14)
式(14)为零时β有以下三个解:
①、β1=0…(15)
②、β2=π…(16)
③、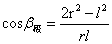 …(17)
…(17)
式(17),仅在r的取值范围为[l/2,l]有意义,其它区域则无意义,于是划分以下区间讨论半径为r的圆上的变化形态。①、l+r0≤r≤R;②、l≤r≤l+r0;③、l-r0≤r≤l;④、l/2≤r≤l-r0;⑤、0≤r≤l/2。下面先讨论不含过小球的圆,后讨论过小球的圆。
(1)在r取值范围为l+r0≤r≤R时,式(13)在β=0时取得极大值,β=π时取得极小值。在l+r0≤r≤R范围内,半径为r的圆上的曲线变化状态见图5左侧半径40,35和右侧45,40,35上诸曲线。各曲线变化特征β=0时,有极大值,由此向两侧对称非线性减小。
(2)在r取值范围为0<r≤l/2时,式(13)在β=0时取得极小值,β=π时取得极大值。图5左侧半径标识为“15”和右侧半径“15”上诸曲线就表示这一变化。其特征是,任意半径为r的圆上的小球行正增量随β的对称增大而对称非线性增大。
(3)在r取值范围为l/2≤r≤l-r0时,式(13)在β=0时,取得极小值;β极=arccos[(2r2-l2)/r/l]时,取得极大值;β=π时取得极小值。图5左侧图标识半径为“20”,右侧图半径为“17.5”、“20”、“25”诸曲线就表示这一变化。
(4)在r取值范围为l-r0≤r≤l时,半径为r的圆经过小球,过小球的小球平行正增量为:
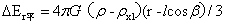 …(18)
…(18)
在β=0时,该式取得最小值,随着β增大,该式的值也不断增大。到圆O1圆上获得最大值,并于式(13)的值相等。根据r取值范围为l/2≤r≤l-r0时任意半径r上的形态,r取值范围为l-r0≤r≤l时,圆O1外部存在存的形态应部分的相同。而因r的取值范围l-r0≤r≤l,是[l/2,l]的一部分,这时式(13)β极的极大值可能在圆O1圆外、圆内及圆上,所以任意半径r的随着β增大,由最小值对称逐渐增大,到取得最大值或极大值后又逐渐减小。图5左侧标示半径“15”的圆上,图5右侧标示半径“25”、“30”、“35”的圆上,就是其变化形态。
式(18)最大值时β的值通过下面过程求出:式(18)半径为r的圆与圆O1圆有对称两交点,任意一个交点与圆心O的连线与z轴的最小夹角计算如下: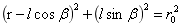 ,解该式得:
,解该式得:
β1=arccos[(r2+l2-r02)/(2rl)]…(19)
(5)在r取值范围为l≤r≤l+r0时,圆O1圆内任意半径小球平行正增量也为式(18),外部则为式(13)。当式(18)随着β增大,式(18)值逐渐增大,到圆O1圆上达到最大值,这时的值与式(13)值相等。结合r取值范围为l-r0≤r≤l和l+r0≤r≤R任意半径r的小球平行正增量的形态,r取值范围为l≤r≤l+r0时任意半径r的小球平行正增量的形态,随着β增大而增大,到圆O1圆上达到最大,然后随着β进一步增大,开始减小直至最小。这一变化见图5左侧半径标示“40”和右侧半径标示“35”、“40”的曲线形态。
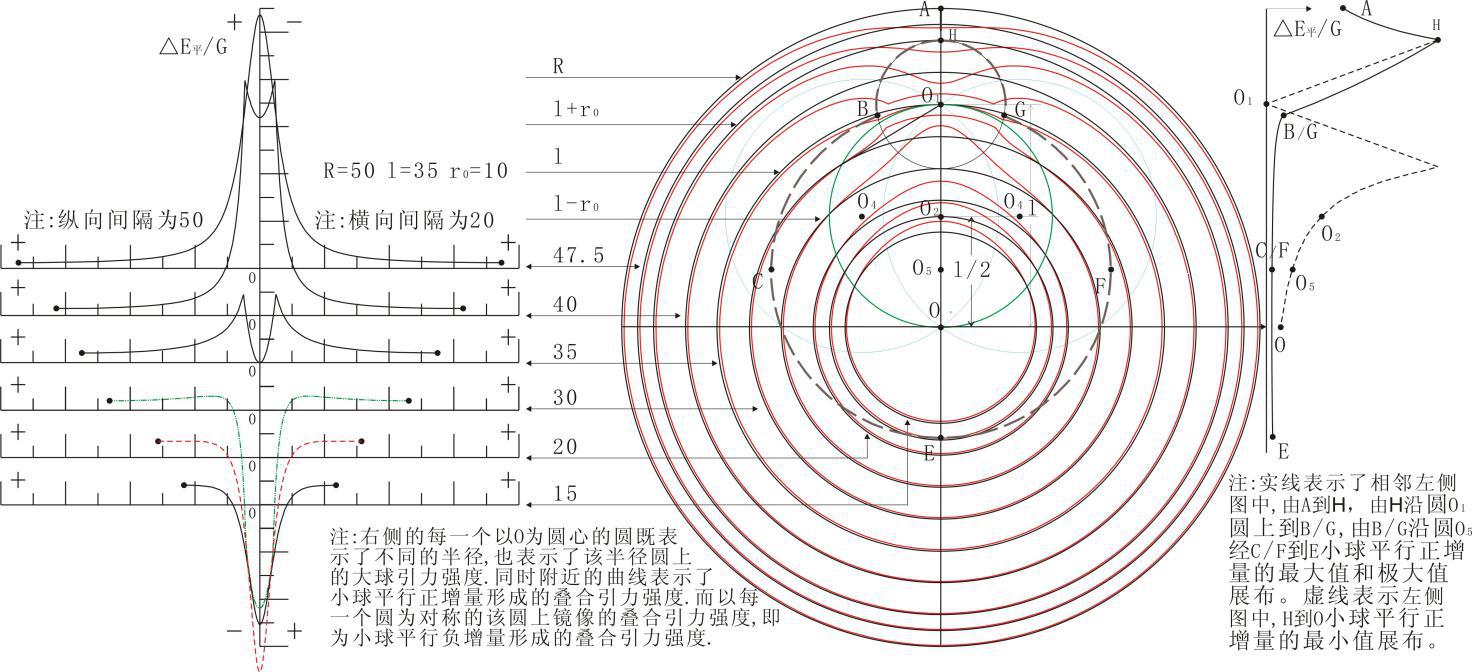
图5 小球平行正增量球内同半径球面上展布剖面示意图
Ⅱ、沿z轴小球随半径的增大,根据上面的讨论,与大球引力强度同向的小球平行正增量0≤r≤l-r0范围内逐渐减小,到r=l-r0时达到最小。尔后随r的增大到O1时,小球平行正增量为零。之后小球平行正增量与大球引力强度反向,随随r的增大而增大到r=l+r0时达到最大,尔后随r的增大而减小。这一特点图5右上侧以虚线给出了变化形态。
Ⅲ、r取值范围为[l/2,l],β=β极时式(13)取得的极大值具有以下变化规律。该极值在图6的坐标系可表示为:
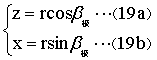
解式(17)和式(19)消去r和β极,得如下平面方程:
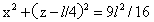 …(20)
…(20)
上式为一圆方程,见图6中圆O5。圆O5与圆O1交点到O点的距离为:
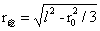 …(21)
…(21)
2.3、小球平行正增量展布特征总结
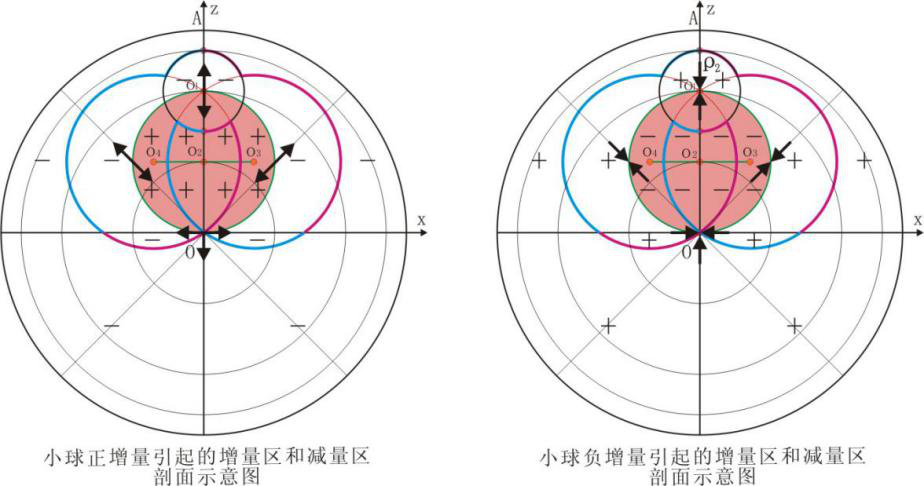
图6
小球平行负增量与小球平行正增量仅差一个负符号,所以小球平行负增量的以上两种展布调向即为小球平行负增量。通过以上分析发现,图7圆O2的圆内小球平行正增量与大球引力强度同向,叠加后的引力强度的绝对值相对与大球引力强度绝对值增大;而在以外的大球剖面区域上,叠加引力强度绝对值相对与大球引力强度绝对值减小。前者命名为增量区,以“+”表示,后者命名为减量区,以“-”表示,见图6左侧图。小球平行负增量与上述所有结论与上相反,见图6右侧图。从图6可以看到:左侧图“负阴抱阳”,右侧图“负阳抱阴”。所以小球平行正增量在大球内的展布称负阴抱阳性;小球平行负增量在大球内的展布称负阳抱阴性。在这种负阴抱阳或负阳抱阴区域中以小球周边的小球增量变化最为剧烈。于是可归纳出如下性质:1、负阴抱阳性或负阳抱阴性;2、小球平行增量小球周边变化剧烈性。3、底半圆小球增量的平均变化小于上半圆。这一性质命名为小球平行正(负)增量性质。
3、大球内小球垂直正增量计算及展布
小球垂直正增量计算及展布分两方面叙述。一是大球内沿任意大球直径上的计算及展布,二是种为大球内同一半径上计算及展布。坐标系的选定同前的设定。
3.1、大球内任意直径上小球垂直正增量的计算及展布
图2-4中,大球内任意过O直径上和不含圆O1圆内部分直径上的小球垂直正增量,以GG'为例,计算式为:
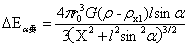 …(21)
…(21)
上式对X求一阶导数得:
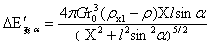 …(22)
…(22)
上式等于零有极值,所以X极=0。
式(22)不考虑物理意义的前提下,X=0+,式(22)小于零,所以式(21)在X=X极时有最大值,这一最大值均在圆O2上,由原点向两侧非线性减小。图2-4中不经圆O1的任意直径上小球垂直正增量展布特征,见图7中DD'或PP、GG'或TT'、JJ'。
图2-4中经过圆O1的任意直径上,圆内部分的小球垂直正增量为:
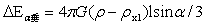 …(23)
…(23)
X取值范围在0到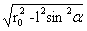 ,式(23)为一定值。在圆O1的圆上式(21)与式(23)相等,由于式(21)的数学意义上的最大值在圆O1圆内,所以(21)的最大值也为式(23)。所以图2-4中任意经O过圆O1的直径上小球垂直正增量展布,见图7中BB'或MM'。当式(21、23)中α为零,两式都为零,所以AA'上无变化曲线。
,式(23)为一定值。在圆O1的圆上式(21)与式(23)相等,由于式(21)的数学意义上的最大值在圆O1圆内,所以(21)的最大值也为式(23)。所以图2-4中任意经O过圆O1的直径上小球垂直正增量展布,见图7中BB'或MM'。当式(21、23)中α为零,两式都为零,所以AA'上无变化曲线。
3.2、大球内任意半径圆上小球垂直正增量的计算及展布
上面分析了大球内直径上小球垂直正增量的展布特征,下面分析小球垂直同半径上展布特征。坐标设定同前。
Ⅰ、图5中,不经圆O1任意半径r上,存在两个区间[0,l-r0][l+r0,R]。A点或B点上的小球垂直正增量为:
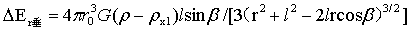 …(24)
…(24)
上式中对β求一阶导数得:
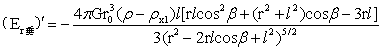 …(25)
…(25)
上式为零时有意义的解为:
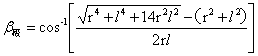 …(26)
…(26)
根据上面的讨论可知,任意半径上,随着β的增加,式(24)有零增加到β=β极得极大值,过此又非线性减小。于是任意半径r上的小球平行正增量展布,根据对称性,见图8左侧图中标注半径:47.5、20、15和右侧图中半径50、47.5、45、25、17.5、15的相应圆上的曲线。
式(24)的不考虑物理意义时,每一半径的极值点可通过下面的方法求得在xz平面的表达式。由于Z=rcosβ极,X=rsinβ极,消去β极,可得如下的平面方程:
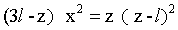 …(27)
…(27)
其曲线形态见图8中右侧“8”字上开口型蓝色线表示的形态。
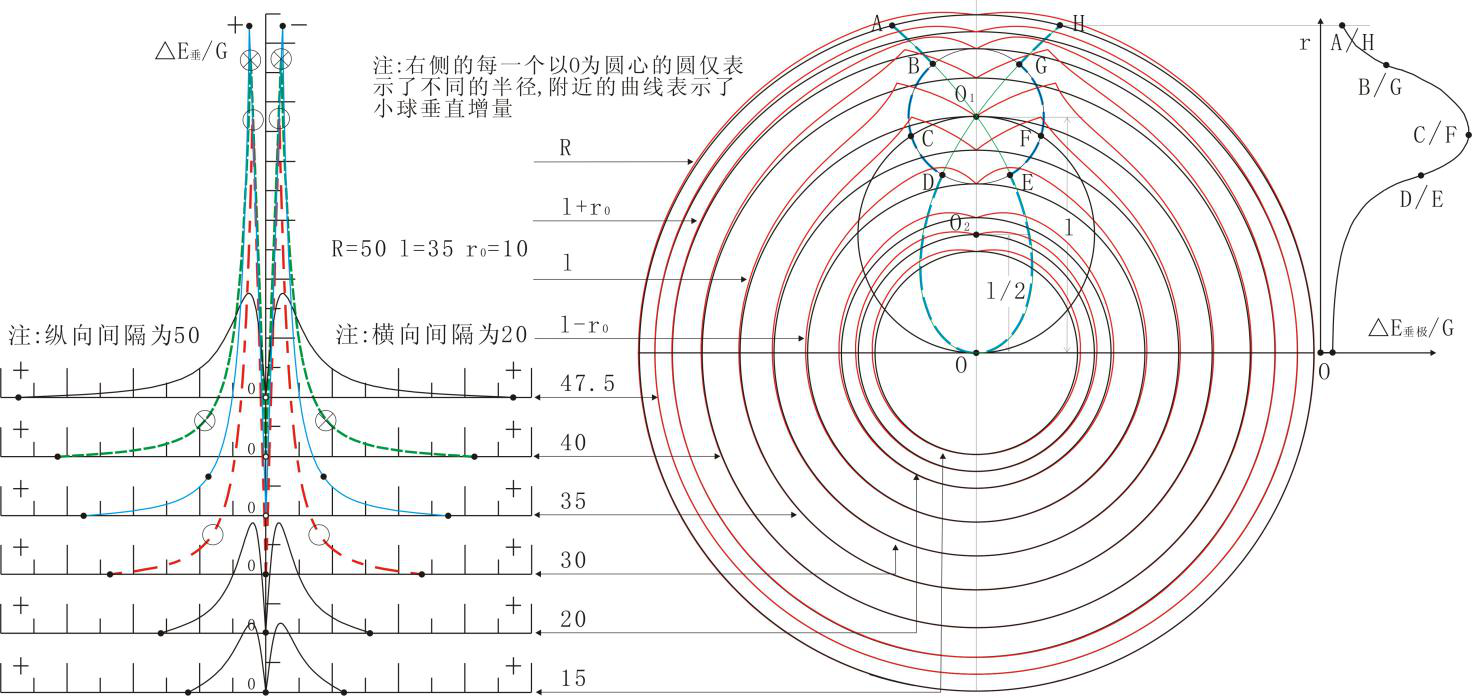
图8 小球垂直正、负增量同半径上的剖面展布示意图
Ⅱ、任意半径r在[l-r0,l+r0]区间上,这时的圆经过小球,过小球的部分的小球垂直正增量的表达式为:
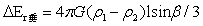 …(28)
…(28)
式(29)在图2-4圆O1内,随β的增大而增大,在圆O1圆上式(28)与式(24)相等。图2-4圆O1上任意点与O的连线的与AO的夹角为:
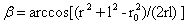 …(29)
…(29)
式(29)β的最大角度值是图2-4切线DO与AO的夹角arcsin(r0/l)。
在图2-4圆O1圆上式(28)与式(24)相等,这一等式将式(26)带入其中,就得式(24)在圆O1圆上取得极大值的点,这一点距图2-4的大球球心的距离为:
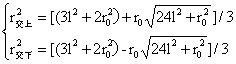 …(30)
…(30)
图2-4以O为圆心半径为r经过O1的圆,r在区间[l-r0,r交下]和[r交上,l+r0]和方程(27),式(24)极大值在圆O1的圆外;r在区间[r交下,r交上]和方程(27),式(24)极大值在圆O1的圆内。由此可以得到:图2-4小球垂直平行正增量,以AO为对称,随β的增大而增大,过此随β的增大而减小。这一变化形态见图8左侧图和右侧图所标示半径为“30,35,40”上的曲线。最大值沿A→B→C→D→O不同半径上的变化见图8右上侧的展示。
3.3、小球垂直正增量展布特征总结
通过以上对小球垂直正增量在大球内的展布分析,可以知道大球内小球垂直正增量任意半径上以z轴为对称,变化最大的区域图8中如带角甲壳虫区域附近。所有点的小球垂直正增量以z轴对称,上半圆呈一定角度的镜像背离,下半圆小球垂直正增量呈一定角度的镜像相对,见图9左侧图的展布。这种上半球的镜像背离为阴的话,下半球的镜像相对则为阳,这样就形成阴阳相偎。对于小球负增量,则有阳阴相偎。于是可归纳出小球垂直增量性质:1、阴阳相偎性或阳阴相偎性;2、小球垂直增量小球周边变化剧烈性。这一性质命名为小球垂直正(负)增量性质。
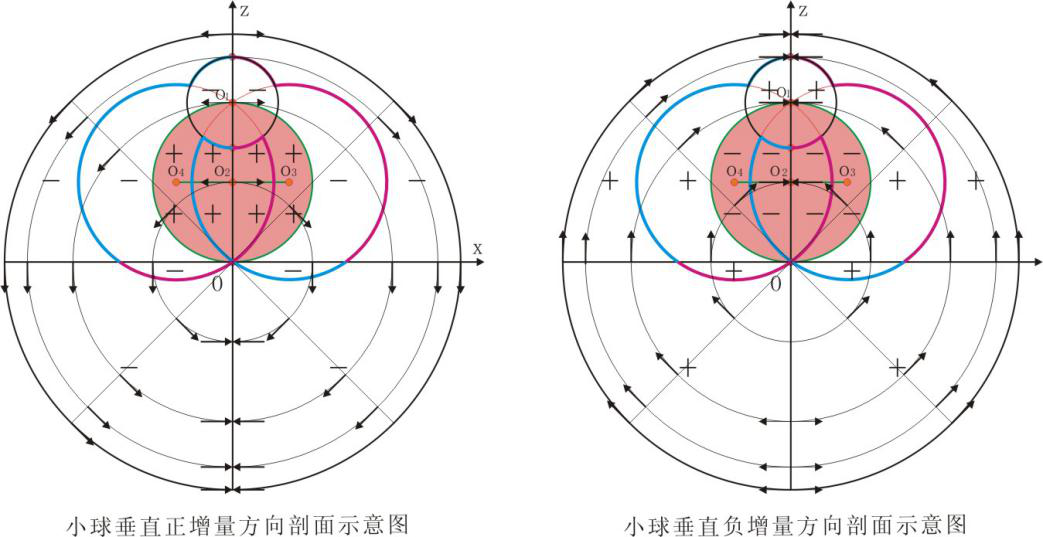
图9
https://wap.sciencenet.cn/blog-3433895-1517627.html
上一篇:地球系统力学动力学(1)
下一篇:地球系统力学动力学(3) 第三部分 球层的形成及含球层的球内性质