柱坐标系下物质的上升与下降形成的引力场再分析

李务伦

吉林省煤田地质局二零三勘探队

以往物质的上升与下降的成因讨论，麻烦且啰嗦，下面基于柱坐标系再讨论。可以看到柱坐标系的分析讨论能更好理解异密度物质的上升与下降，下面用柱坐标系进行再分析再探讨。敬请批评指导！

图1是均匀密度为ρ，半径为R的球。球内、外引力强度表达式如下：

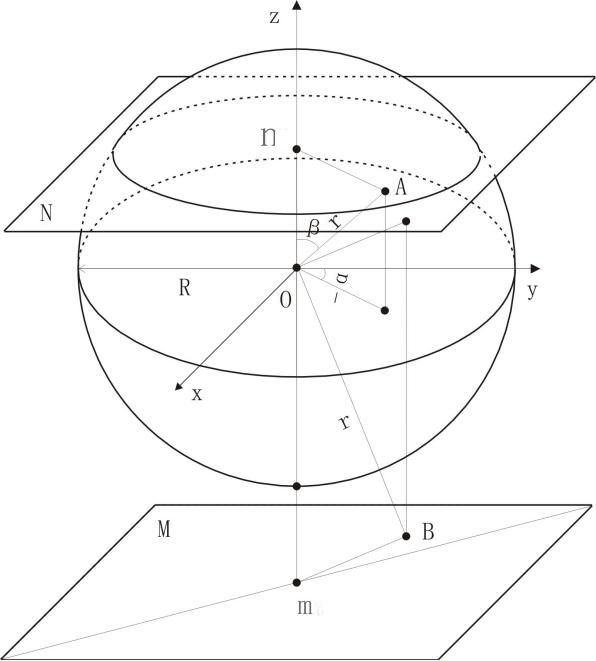
图1

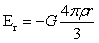  （r≤R）…（1）

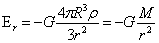  （r≥R）…（2）

（一）、图1中的B点位于M平面内，位于球外。B点平行于z轴的分量E_z通过计算表达式为式（3）；B点平行于xy平面的分量E_xy通过计算表达式为式（4）。

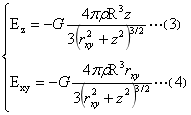
①、式（3）｜z｜=｜z_m｜≥R时，平面M的方程为z=z_m，其上平行z轴的分量随r_xy的增大，当｜z_m｜≥R，E_z由极小值向四周逐渐变大，经z轴上剖面上E_z的曲线形态类似正态曲线[见图2（1）（2）黑色曲线]，E_z方向指向xy平面。②、式（4）r_xy≥R时，z=0时E_xy有极小值，由此向上、下，E_xy逐渐变大，经过z轴的剖面上E_xy的曲线形态类似正态曲线[见图2（2）、（3）黑色曲线]，E_xy方向指向z轴。这也不完全讨论了图1球外的情况。

（二）、图1中的A点在球内位于平面N上。A点平行于z轴的分量E_z通过计算表达式为式（5）；A点平行于xy平面的分量E_xy通过计算表达式为式（6）。

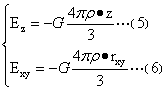
①、式（5）E_z与r_xy无关，仅与z有关，平面N距O的距离等于z₀时。平面N与球O的交线内部为定值，即r_xy≤（R²-z₀²）^0.5范围内E_z为定值，E_z方向上半球、下半球均指向平面xy。当r_xy≥（R²-z₀²）^0.5时，平面N上E_z的变化由（3）来计算，式（3）在平面N与球O的交线上的值与上述所述相等，由交线上定值，上半球向四周随r_xy的增大逐渐增大，下半球向四周随r_xy的增大逐渐减小。这一变化见图2（1）、（2）红色曲线的形态。②、式（6）E_xy与z无关，仅与r_xy有关。当r_xy=r_xy0（＜R），E_xy在r_xy=r_xy0圆柱面上为定值，方向都指向z轴。平面方程z²=（R²-r_xy0²）与球O的的上下两交线的值，与方程（4）相等。由此向上、下，E_xy逐渐变大，经过z轴的剖面上E_xy的曲线形态类似正态曲线水平截取含极大值后的部分[见图2（2）、（3）红色曲线]，E_xy方向指向z轴。

小球密度与大球相同，这时的大球内外引力强称为大球引力强度，少计或多算的小球质量球内、外引力强度称为小球增量，少计的小球质量引力强度为小球正增量，方向背离小球球心；多算的小球质量引力强度为小球负增量，方向指向小球球心。大球引力强度（以图2 O为坐标原点）和小球增量（以图2 O₁为坐标原点）表达式如下：

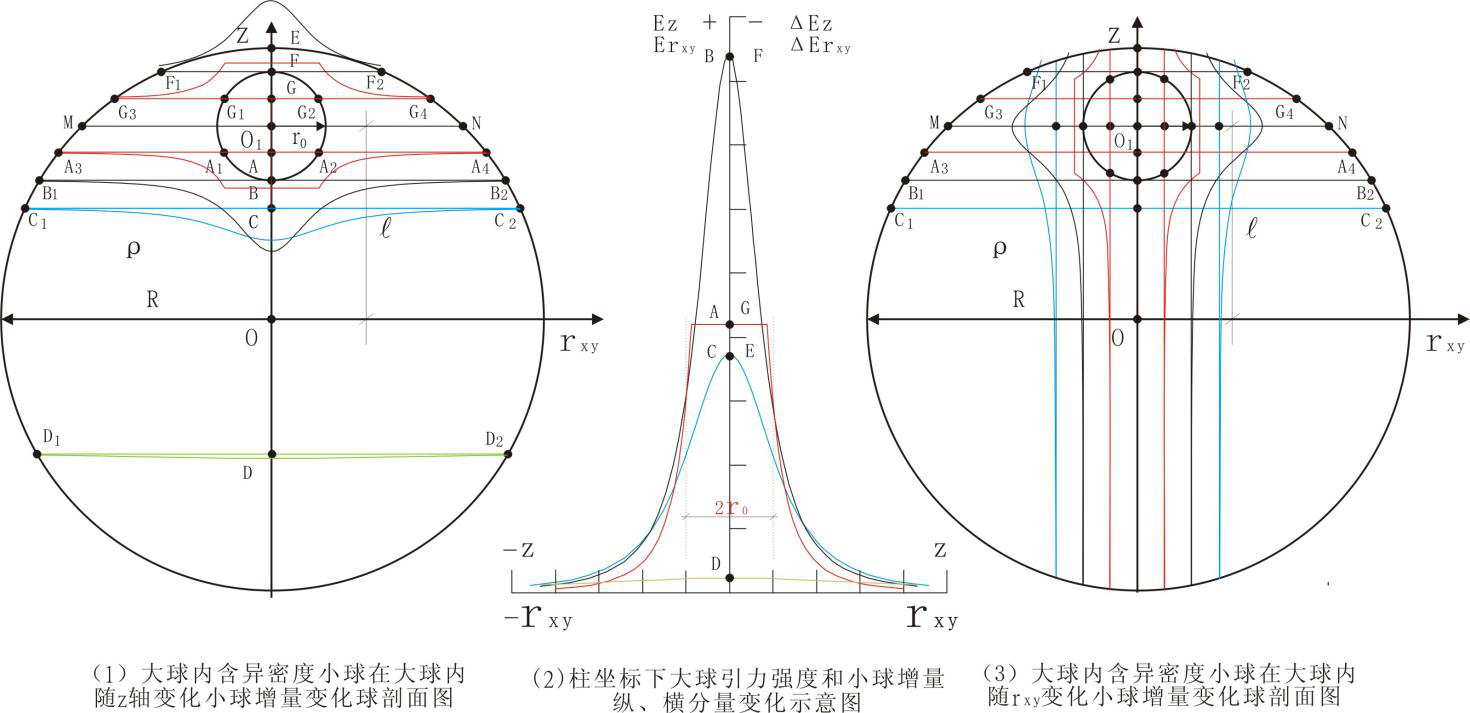
图2

大球引力强度为式（1）和（2），小球增量以O₂为坐标原点，表达式为：

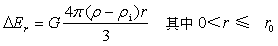…（7）

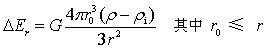…（8）

改为柱坐标系后，式（7）的表达式为：

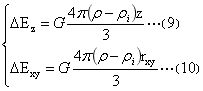
改为柱坐标系后，式（8）的表达式为：

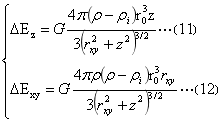
（二）、式（9）、（10）和（11）、（12），根据前面的讨论，它们在大球内的变化情态见图2。图2（1）剖面表示了不同平行xy平面上小球△E_z的变化情态。小球正增量△E_z，平面MN下，小球正增量△E_z的方向与大球引力强度Ez同向；平面MN上，小球正增量△E_z的方向与大球引力强度E_z反向；变化最大在小球的地方在小球顶底部。图2（3）剖面表示不同柱面上△E_z的变化情态。小球正增量△E_xy，不同r_xy=r_xy0下，小球正增量△E_xy的方向与大球引力强度E_xy方向相反；平面MN上，小球正增量△E_z的方向与大球引力强度E_z反向；变化最大在小球的地方小球左右两侧。小球负增量△E_z、△E_xy与小球正增量△E_z、△E_xy仅是方向的不同，其余不变。

前面已厘清小球正增量△E_z、△E_xy和大球引力强度E_z、E_xy于球内、外的变化，下面就利用厘清的力场规律分析异密度的上升与下沉的成因。

（一）大球引力强度E_z于图1、2大球内，E_z在过O平面xy为零，随z在-R到R间的变化的每一平面上为定值，上半球的大球引力强度E_z方向平行z轴，即垂直于过O的xy平面，下半球则与之相反，这在纵向上保证了大球内所有质点的稳定与平衡。而对于小球正增量△E_z，在小球正增量△E_z在大球内部变化规律见图2（1）。过O₁的平面xy在大球内部上部小球正增量△E_z方向与大球引力强度E_z方向相反，其下部在过O平面xy间方向则相同，过该O平面xy小球正增量△E_z方向又相反。方向相同的，叠加后的引力强度增大，相反则变小。这样一来就改变了大球内的所有质点的稳定与平衡，引力强度增大的地方较原有稳定平衡的压力增大，否者减小。减小部位以小球顶部最为大，其它部位相对较小，增加部位以小球底部增加最大，这样一来小球就获得了上升的动力，小球因此而上升。对于

（二）大球引力强度E_xy于图1、2大球内，E_xy在z轴为零，随r_xy在0到R间的变化的每一圆柱上为定值，E_xy方向平行xy平面，即圆柱面任意点方向指向并垂直于z轴，这在横向上向上保证了大球内所有质点的稳定与平衡。小球正增量△E_xy在上述的每一圆柱面上的变化见图2（3），任意点的方向背离z轴，与E_xy相反，这样一来就改变了原有圆柱上的平衡与稳定，改变最大的地方在图2（3）图示的小球周边。由于E_xy与△E_xy方向相反，使得小球水平的周边压力减小，为小球的上升提供方便及助力。

（三）通过以上的分析可以得到，当小球的密度小于大球，存在于大球中的小球，因引力场的改变使得小球具有上升的动力，否者，当小球的密度大于大球，由于小球负增量与小球正增量方向反，调改上分析的方向就得到小球的下降分析过程，因此不再单独赘述。

通过上面分析，可以发现较过往的分析，该分析方法较为简单和直观，可方便的理解异密度物的力场下的物体上升与下降。具体的上升力与下降力以往已给出，不再讨论。无论小球是升是降，以往提出的动力学等也可依据上述讨论也可分析得出，故也不在讨论。如有不当请老师们批评指导！