我不同意高宏老师9月20日博文的观点

我理解高宏老师把随机过程/布朗运动/维纳过程作为重要研究方向，希望取得大突破。然而要做大事就要有格局，需要多听不同意见。这次我又来说不同意见，但不指望高老师会来细看。希望网友多提意见。例如文字图片是否易懂，是否在理和有根据。如果是“胡搅蛮缠”或者“基本概念完全不清和逻辑思维异常混乱”（高老师评语），请严肃指出，我一定会诚恳认错改错和道歉。 

高老师这篇博文的主要目的是批评维纳用“时间函数”和“随机变量”这两个完全不同的概念描述同一个布朗粒子在t时刻的位移X(t)。因此说维纳违反矛盾律的逻辑错误。下图引自高老师博文：

 但是我认为，虽然时间函数和随机变量是两个概念，却并非互相矛盾和不能相容。而随机过程的研究对象正是“随机时间函数”！

 一、  以名著的文字和图片说明“随机时间函数”是随机过程的研究对象

这本书是1976年科学出版社出版，原作者潘契夫（S.Panchev）。著名数学力学家谈镐生院士领衔翻译的《随机函数和湍流》。下面两张图片都影印自此书第27页。

请注意图中标题就是“随机函数”。说概率论原来研究的随机变量不考虑参数（时间或其它参数）。但物理学的发展必须研究依赖参数（特别是时间）的随机变量。。。。。对于自变量的给定值，函数值为随机变量的那些函数就是随机函数，其观测结果由随机函数来表示的物理过程，则称作随机过程。可见，如果否定了“随机时间函数”，其实就否定了“随机过程”的研究对象！

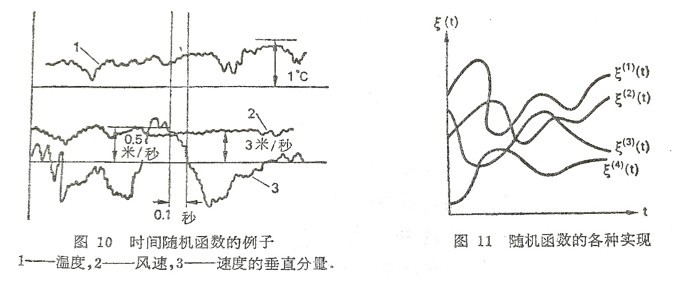
这张图也影印自第27页。左图以气象部门常规监测得到的气温和风速曲线作为随机时间函数的例子。右图是4条随机函数的各种实现（试验结果，因此是已知的时间函数曲线）。下面利用它解释样本函数和随机变量/随机过程的关系。

二、随机过程、样本函数和随机变量的关系

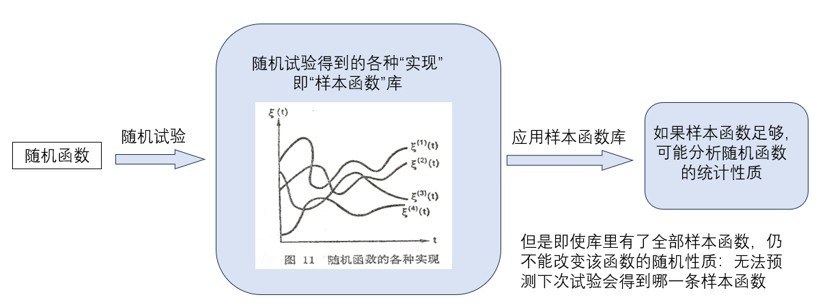
高老师写9月15日博文回复我上篇博文中的“疑问2”，我们进行了热烈讨论。但他批评我不知道“矛盾律”，没有最基本的逻辑思维能力。下面我画2张图，比较最简单的硬币投掷和假设的随机时间函数（环境气温）监测。说明：随机变量→通过随机试验→得到样本库→用来分析随机变量的统计性质。但即使得到了全部样本，随机变量还在那里。因为仍然不能预测再做投掷会得到硬币的哪一面。同样，随机函数→随机试验→得到样本函数库→样本库可用于对随机函数进行统计分析。但即使有了大量样本函数，那个随机函数还在那里，下次试验仍然不能预测会得到怎样的曲线

投掷硬币：

环境气温监测：

我用这两张图解释，研究的是随机变量或随机函数。随机试验的结果对应“样本”或“样本函数”。样本库或样本函数库可以用来对研究对象进行统计分析。但研究对象还是“随机变量”或“随机函数”。

我买了多本高老师在博文提到过的中文教材。其中只有一本，解释随机变量和样本函数时，确实存在问题。我认为把布朗运动位移试验结果称为样本函数是正确的，但不能因为样本函数是已知的“时间函数”，就认为布朗粒子位移就是确定的时间函数了。所以我认为这些教科书在后面把布朗运动位移称为随机函数是正确的。

三、请注意维纳过程的特色和创新

我有流体力学基础，曾涉及湍流理论的研究，还曾主要研究湍流扩散和污染气象问题。因此虽然没有认真学习过布朗运动，高宏老师的博文我是相当注意的。为学习我下载了爱因斯坦理论的原文影印件（英文翻译版），和维纳的代表作。弄清了维纳是否偷窃或抄袭了爱因斯坦工作的疑问（见我7月14日博文），但学习维纳的代表作遇到困难：大量的泛函数学不能很快接受。但他代表作的标题很有特色：“微分空间(Differential-Space)”。很奇怪为什么涉及微分空间？（见我7月23日博文）

另一方面，布朗运动的监测十分困难。随科学技术的发展，特别是光镊技术，详细观测布朗粒子运动成为可能。2010年李统藏文章说进行了40兆次的粒子位置观测，真是一个大好消息。但问题来了：即使如此巨量的试验结果，也只是一条“样本函数”曲线，怎样进行统计分析？其次，40兆次，也是有时间间隔的。但可以想象，布朗粒子的位移一定是连续发生的，即理论上说，40兆次的记录，还不是一条“连续”的位移曲线。。。。。如果随机时间函数是连续的，应当怎样在理论上建立一个“有极限”的观测要求？可以想象，随机连续函数通过试验得到的曲线（样本函数）可能相当长，但数量不会多。例如40兆的位置记录，李统藏团队根据什么理论和模型进行的统计分析？

因此这些天有个想法：随机时间函数经常是连续的，试验记录却多是离散的。维纳的主要贡献可能就在这里，提出“微分空间”的理论和方法，因此可以数值模拟布朗运动的轨迹曲线。我在继续学习。

此外，当年牛顿创建微积分理论，应用“无穷小量”，逻辑模糊。受到英国大主教的强烈攻击，引发了100多年的“第二次数学危机”。最后由柯西，魏尔斯特拉斯等数学家以“极限” 理论代替“无穷小量”，辅以严格的语言解决了这个逻辑问题。这是牛顿没看到微积分理论内在的真正逻辑基础，并非该理论本身有逻辑矛盾。因此后人称之为“贝克莱悖论”而不是“牛顿悖论”！