THEORY OF OXYGEN TRANSPORT TO TISSUE - PMC
科学网—氧气在人体内运输的理论 之一 (氧气和血红蛋白结合) -
六、特定组织与器官中的氧转运模型
A. 骨骼肌
骨骼肌(更广泛地说,横纹肌)的一个典型特征是:其毛细血管床的结构相较于大多数其他组织更为规则。肌纤维具有特定的收缩方向,而毛细血管往往沿肌纤维方向分布(Wiedeman[189])。这种解剖结构恰好适用于克罗格提出的简单几何模型[102](见图13)。
骨骼肌的生理状态可在静息到最大工作强度之间连续变化。运动时,血流量和氧气消耗速率均可增加一个数量级,同时功能性毛细血管的数量也会发生改变[50]。过去70年间,克罗格模型被广泛用于定量预测不同生理条件下肌肉内的氧分布[59]。然而,多年来研究人员发现了若干需要重新评估该模型的因素,其中最重要的包括:转运异质性、毛细血管内氧转运阻力,以及肌红蛋白对氧转运的促进作用(Honig等人[72])。
克罗格本人深知毛细血管床的解剖学不规则性——尤其是存在与肌纤维走向不一致的毛细血管吻合支,以及毛细血管血流动力学的异质性[103]。但直到近十年,研究氧转运异质性的理论基础才得以建立。Grunewald与Sowa[56]研究了由四根毛细血管供血的微循环单位(见图16)内的氧分布。他们生成了不同微循环单位的氧分压(PO₂)直方图,并与“通过组织电极在人体静息肌肉中测得的氧分压直方图”进行对比。当将不同微循环单位对应的氧分压直方图按特定比例进行加权平均后,模型结果与实验数据达到了最佳吻合。
然而,将组织视为“不同微循环单位的集合”这一假设,与施加在微循环单位侧边界的“无通量边界条件”存在矛盾。事实上,已有研究表明,相邻的不同微循环单位之间可能存在大量的氧气交换[140]。该模型还被用于其他骨骼肌氧交换的研究中[113,114]。
Klitzman等人[94]分析了“在灌注状态下的仓鼠提睾肌(静息与收缩状态)中,通过氧微电极获取的数据”。当氧分压测量与活体显微镜结合(以确定微电极相对于毛细血管的位置)时,测量范围仅限于从组织表面向下延伸的几层肌纤维深度。组织表面附近的氧分布可能会受到表面灌注溶液的影响。分析中采用的模型考虑了表面的氧交换过程(Popel[139])(见图22),模型中毛细血管呈同向流动且按正方形阵列排列。
实验数据包括“毛细血管静脉端附近组织中的氧分压测量值”,这些数据被用于估算氧气消耗速率和毛细血管入口氧分压——这两个参数在实验中均未直接测量。有趣的是,模型预测的静息肌肉毛细血管入口氧分压约为30托,这与其他“毛细血管前存在大量氧损失”的实验和理论报道一致。
图23a展示了在三种不同组织表面氧分压(Ps)下,计算得出的毛细血管氧分压分布;同时还展示了“克罗格模型在相同参数下的预测结果”,二者的唯一差异在于:克罗格模型假设肌肉表面对氧气不通透。图23b展示了“穿过静息与收缩肌肉中毛细血管静脉端的平面内”的氧分压等压线。显然,灌注溶液对组织表层的氧分布具有重要影响(尤其是在Ps值较高时),在数据分析中应予以考虑。
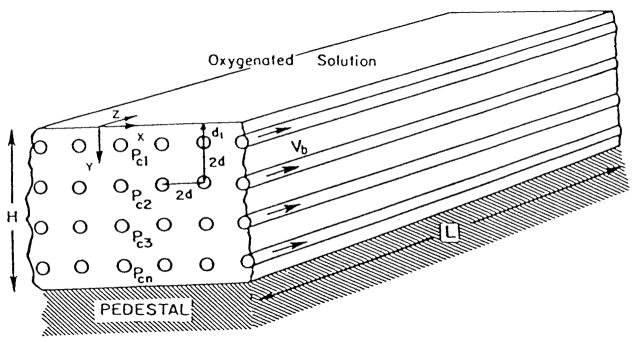
图22.仓鼠提睾肌(含氧溶液覆盖)的几何模型
该模型包含n层毛细血管。假设毛细血管彼此平行且流向相同。肌肉表面的氧分压(PO₂)为已知条件。(数据来源:Klitzman, B.、Popel, A. S. 及 Duling, B. R.,《微血管研究》(Microvas. Res.),第25卷,第108页,1983年。经许可引用。)
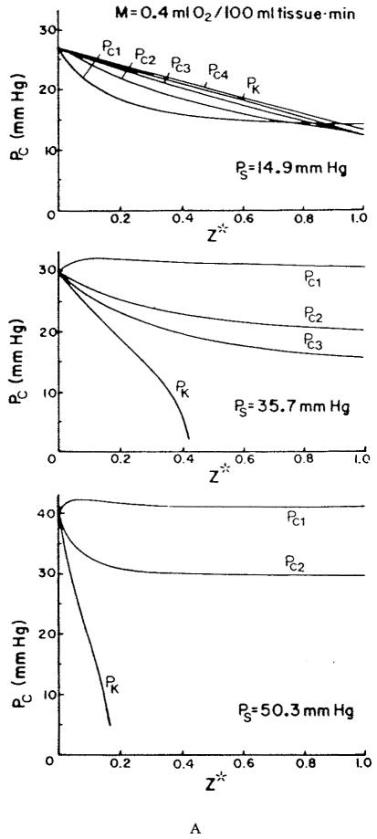
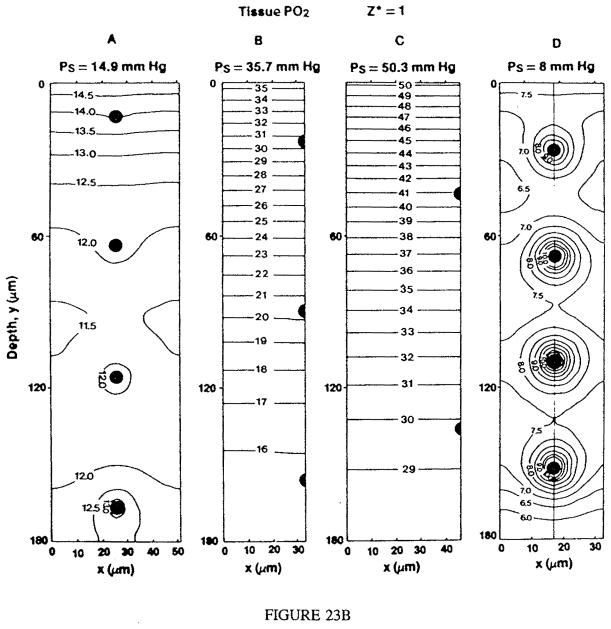
图23.(a)对于图22所示的几何结构,在三种肌肉表面氧张力(Ps)条件下,各毛细血管层的预测毛细血管内氧分压(Pci)随毛细血管轴向位置(z*)的变化关系。图中还展示了克罗格圆柱模型(Krogh cylinder model)预测的毛细血管内氧分压值(PK),该模型假设不存在来自表面的氧气供应。(b)在不同表面氧张力(Ps)条件下,毛细血管静脉端(z* = 1.0平面)的组织氧分压分布。A至C组对应静息状态下的肌肉,D组对应以1Hz频率收缩的肌肉。图中曲线为氧分压等压线,实心圆点代表灌注毛细血管。(数据来源:Klitzman, B.、Popel, A. S. 及 Duling, B. R.,《微血管研究》(Microvas. Res.),第25卷,第108页,1983年。经许可引用。)
Ellsworth等人³¹采用显微分光光度法,在体测量了仓鼠颊囊牵缩肌中单个毛细血管的氧饱和度,并借助数学模型对数据进行了分析。该模型考虑了一块被平行同向毛细血管穿透的组织(见图24),毛细血管长度分布可为均匀分布或非均匀分布。除忽略轴向扩散外,该模型的推导遵循式82至式84。模型以动脉端血红蛋白饱和度(SO₂)的测量值作为边界条件,并将静脉端SO₂的预测值与实验数据进行对比。结果表明,在静息状态下,对于毛细血管长度均匀的模型(图25a),扩散分流效应显著,以至于动脉端的异质性影响在接近静脉端时几乎完全消失。这与实验结果相反——实验发现,随着向静脉端靠近,SO₂的异质性会增强。然而,研究发现毛细血管路径长度的非均匀性是一个重要影响因素,将其纳入模型后,至少能在定性上与实验数据达成一致。若要进行定量对比,则需要一个能反映更真实路径长度分布的网络模型。对收缩状态下肌肉中氧气传输的模拟显示,异质性产生的影响与静息状态下的预测结果截然不同:在静息肌肉中,扩散分流会消除大多数毛细血管间的差异;而在收缩肌肉中,这种差异会被放大,即使毛细血管路径长度均匀,静脉端SO₂也会出现较大离散度(图25b)。这些预测尚未通过实验验证。
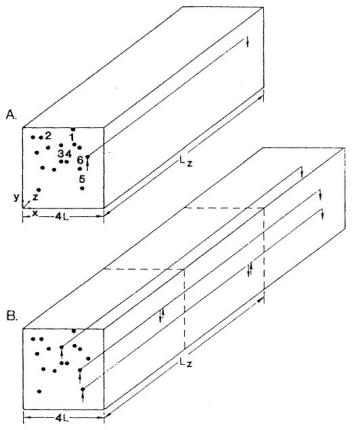
图24.数学模型的几何结构。(a)毛细血管流动路径长度均匀;(b)毛细血管流动路径长度非均匀。为毛细血管分配了红细胞流量和入口血红蛋白饱和度的实验测量值。(数据来源:Ellsworth, M. L.、Popel, A. S. 及 Pittman, R. N.,《微血管研究》(Microvas. Res.),第35卷,第341页,1988年。经许可引用。)
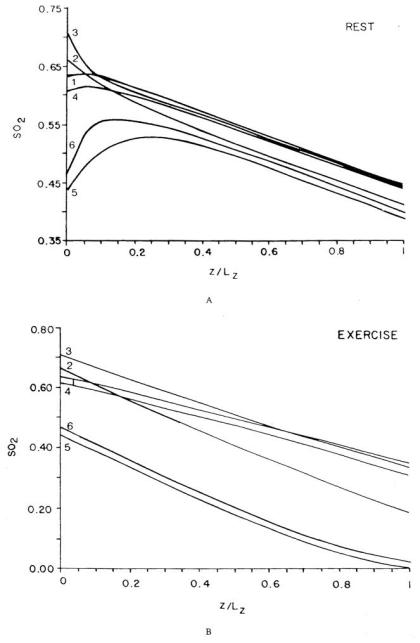
图25.16条平行毛细血管(路径长度均匀,在图24中标记为1至6)中,6条毛细血管的血红蛋白饱和度(SO₂)分布预测结果。(a)静息状态肌肉;(b)收缩状态肌肉。(数据来源:Ellsworth, M. L.、Popel, A. S. 及 Pittman, R. N.,《微血管研究》(Microvas. Res.),第35卷,第341页,1988年。经许可引用。)
长期以来,人们已知并明确肌红蛋白在骨骼肌中具有储存氧气、在氧气供应中断时释放氧气的作用。在克罗格圆柱模型中,研究人员已将肌红蛋白纳入考量,并通过数值方法求解了血管闭塞(血流停止)情况下的模型。然而,肌红蛋白在促进氧气扩散中的作用,是近年来通过数学模型才得以阐明的(另见相关综述)。由于肌红蛋白分子被限制在肌纤维内,无法穿透质膜,因此有研究提出⁸⁵:与克罗格组织圆柱模型相比,“被毛细血管包围的肌纤维”更适合作为基本微循环单元的模型(图26a)。Federspiel³⁴采用犬 gracilis 肌(处于最大呼吸状态)的参数值,通过数值方法求解了该模型问题。模型中,通过将肌纤维表面的氧分压(PO₂)设定为极角坐标的周期函数,来模拟毛细血管的作用。图26b展示了不同总肌红蛋白浓度下,肌红蛋白对氧气扩散的促进效应。结果表明,富含肌红蛋白的肌纤维,即便在肌膜处氧分压较低(仅几托)的情况下,也能凭借肌红蛋白对氧气扩散的显著促进作用,维持较高的耗氧速率。
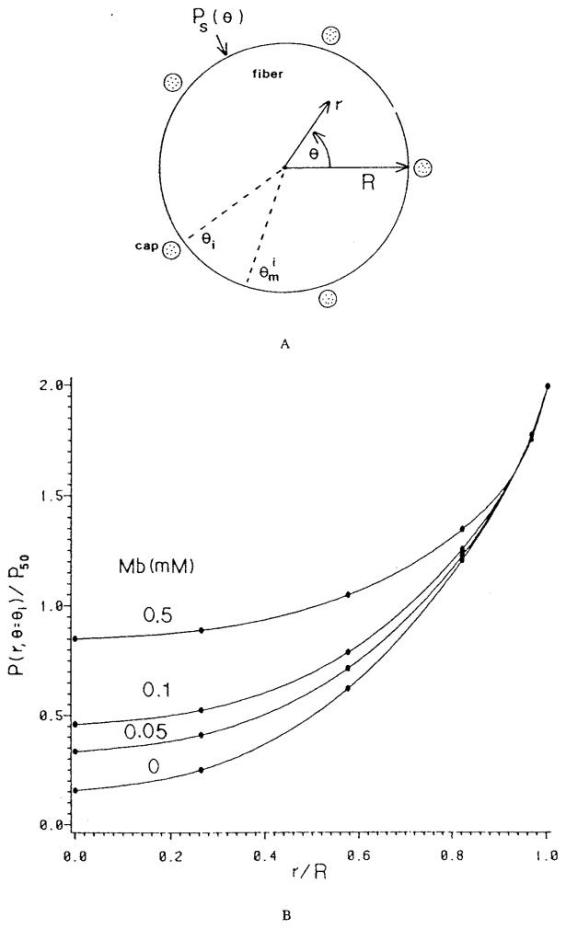
图26.(a)氧气扩散进入含肌红蛋白骨骼肌纤维的二维(r, θ)模型。等间距分布的毛细血管位于θi极角位置,毛细血管中点的极角位置为θim。肌膜处的氧张力PS(θ)沿肌膜变化,以模拟毛细血管对氧气的离散性供应。(b)通过分析以P50归一化的P(r, θ = θ1)径向分布曲线,研究氧张力的最大径向梯度。图中呈现了肌红蛋白浓度的影响。模型参数对应犬 gracilis 收缩肌。(数据来源:Federspiel, W. J.,《生物物理学杂志》(Biophys. J.),第49卷,第857页,1986年。经许可引用。)
在骨骼肌中,线粒体并非在肌纤维内均匀分布,而是以均匀间隔的条带形式集中分布于组织中。Covell与Jacquez²³通过考虑一块组织中氧气消耗的周期性,模拟了肌纤维内线粒体的分布。他们得出的结论是:对于红色骨骼肌(红肌),当氧分压低于10托且处于最大呼吸状态时,肌红蛋白能显著增加向线粒体的氧气输送量。
毛细血管内氧气传输阻力的作用机制已在第二节中讨论。Groebe与Thews⁵¹尝试将这种阻力与肌红蛋白促进的扩散作用一同纳入肌纤维模型(图27a)。图27b展示了“四条毛细血管包围一条肌纤维”模型的计算实例:预测结果显示,氧分压梯度最大的区域位于毛细血管内部及其紧邻区域,而在肌纤维主体部分,氧分压分布曲线较为平缓。这些预测与“犬 gracilis 肌冰冻切片中肌红蛋白饱和度的显微分光光度测量结果”在定性上一致。因此,毛细血管内阻力与肌红蛋白促进的扩散被认定为骨骼肌中氧气交换的主要影响因素,而血红蛋白-氧气(Hb-O₂)的非平衡化学反应可能仅起到次要作用。
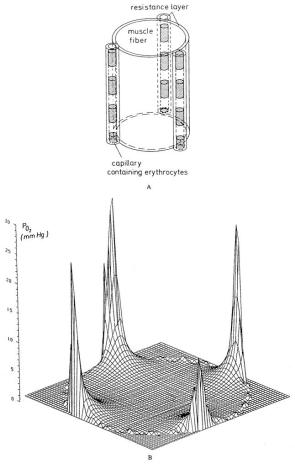
图27.(a)被毛细血管包围的肌纤维几何结构;(b)被四条毛细血管包围的肌纤维横截面内的氧分压(PO₂)分布。肌纤维外环绕着一薄层同心分布的细胞外液。(数据来源:Groebe, K. 及 Thews, G.,《实验医学与生物学进展》(Adv. Exp. Med. Biol.),第200卷,第495页,1986年。经许可引用。)
Groom等人⁵²研究了剧烈收缩肌肉中毛细血管床的血管构筑(angioarchitecture)。他们发现,此时毛细血管会发生折叠,并在每条肌纤维周围形成致密的网状结构。基于这一观察结果,他们提出:对于收缩状态的肌纤维(实心圆柱模型),将肌膜处氧分压设定为均匀值可能是一种合理的边界条件。Piiper与Scheid¹³²对实心圆柱模型与克罗格圆柱模型的预测结果进行了对比。
最后,Roth与Wade¹⁴⁷采用前文讨论过的房室模型(图21),预测了静息状态与运动状态下整个骨骼肌微循环中的氧气分布。计算所用参数来源于多个渠道,并非全部来自肌肉组织。图28展示了在不同动脉氧分压水平下的氧气分布情况。这些计算结果表明:当耗氧速率升高时,毛细血管几乎成为组织唯一的氧气来源,而小动脉与小静脉仅能提供少量氧气;相反,在低耗氧状态下,有相当一部分氧气通过小动脉壁进行交换。
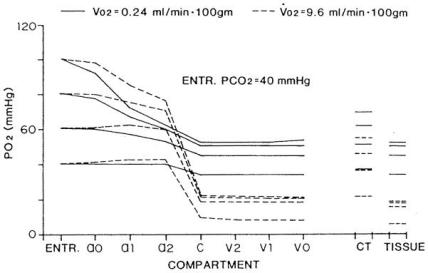
图28.在静息状态(实线)与中度运动状态(虚线)下,不同输入氧分压(ENTR. PO₂)条件下各房室氧分压的纵向分布。CT代表结缔组织房室。(数据来源:Roth, A. C. 及 Wade, K.,《微血管研究》(Microvas. Res.),第32卷,第64页,1986年。经许可引用。)
B. 心肌
由于毛细血管-组织的几何结构相似,上述针对骨骼肌的模型通常也适用于心肌中的毛细血管-组织氧气传输。然而,尽管已知氧气对心脏至关重要³⁶,但专门针对心脏的理论研究却为数不多。
Rakusan¹⁴³采用克罗格模型,评估了不同生理条件下心肌中的氧气分布。他与同事构建了两种模型:一种是“被非圆形组织圆柱包围的毛细血管”模型(克罗格模型的延伸),另一种是“被毛细血管包围的肌纤维”模型(Rakusan等人¹⁴⁴;Hoofd等人⁷⁴)。前文所述的模型⁵⁶(图16)也被应用于心肌研究(Grunewald与Sowa⁵⁷)。Napper与Schubert¹²⁶采用克罗格圆柱几何结构,试图解释“含氧溶液灌注心脏中,通过氧气微电极测得的实验性氧分压分布”。由于心肌中毛细血管间距较小,模型假设组织圆柱横截面内的组织氧分压均匀,但考虑了轴向扩散。然而,为了使理论氧分压直方图与实验氧分压直方图达成一致,模型不得不采用比公认值大10倍的扩散系数。
Wieringa¹⁹⁹考虑了一个由平行毛细血管构成的大型网络,这些毛细血管通过吻合支(anastomoses)相互连接。小动脉输入端与小静脉输出端随机分布。对毛细血管网络中血流的模拟结果,与冠状动脉微循环中实验测得的血流分布在定性上具有相似性,尤其呈现出逆流(countercurrent flow)模式。在氧气扩散计算中,模型忽略了轴向扩散,且未考虑吻合支除影响血流分布外的其他作用;同时,也未纳入肌红蛋白的促进扩散作用与毛细血管内阻力。该模型通过有限元法(finite element method)进行数值求解。
C. 脑
大脑是一种正常功能高度依赖氧气持续供应的器官。与骨骼肌可在无氧条件下存活数小时不同,脑细胞在缺氧开始后的几分钟内就会出现不可逆损伤。因此,理论研究对于理解“正常与缺氧条件下,氧气在大脑不同结构中的分布规律”具有特殊重要性。
大脑氧气传输的理论研究始于克罗格方程的应用(Opitz与Schneider¹³⁰),随后研究人员将克罗格模型扩展到“六边形填充组织圆柱”(Thews¹⁷⁷)。Reneau及其同事采用克罗格模型,对大脑中的氧气传输进行了系统分析⁹⁶ˌ¹⁴⁵ˌ¹⁴⁶。他们通过数值有限差分法(finite-difference method),求解了具有生理意义的稳态与非稳态问题,图14展示了部分计算实例。
然而,大脑毛细血管网络的构筑特点并不支持克罗格模型的假设。研究人员因此构建了其他模型,以反映毛细血管构筑与血流动力学的异质性。Metzger¹²⁰提出了一种用于大脑微循环单元的立方晶格模型(图18)。该模型通过应用基尔霍夫定律(Kirchhoff’s laws)计算毛细血管中的血流,从而模拟血流异质性(尽管采用了理想化的模拟方式)。Kislyakov与Ivanov⁹³对Grunewald与Sowa⁵⁷此前提出的“四毛细血管微循环单元”模型进行了调整,以模拟“被神经胶质细胞团包围的球形神经元”(图29)(另见Kislyakov⁹¹;Ivanov与Kislyakov⁸³)。神经元内的耗氧速率约为神经胶质细胞的10倍,这一差异对氧气分布具有显著影响。Ivanov等人⁸⁴的模型纳入了更贴近真实的毛细血管-细胞结构几何形态,图30展示了该模型的一个实例——纺锤形神经元周围分布着两条毛细血管。该模型中神经元与毛细血管的几何参数可直接来源于三维解剖重建研究。此外,该模型还被用于研究“血流变化与神经元呼吸活动改变时,氧气传输的动态过程”⁹²。在该研究团队开展的这些及其他研究中,对毛细血管传输过程的处理方式与式83、式84的描述不同——其模型推导并非基于严谨的质量平衡方程。因此,尽管这些模型⁸⁴ˌ⁹³的几何结构相比克罗格模型有了显著改进,但模型结果可能会以未知的方式依赖于“对毛细血管传输过程的特设性处理”(ad hoc treatment)。
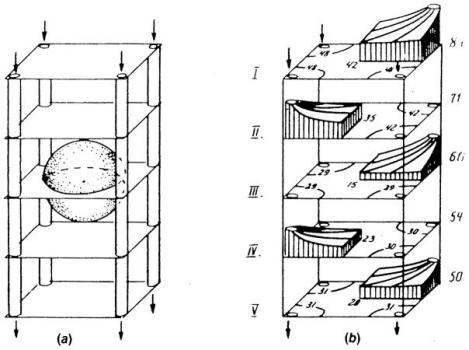
图29.(a)以球形神经元为中心的微循环单元示意图;(b)该单元横截面内的氧分压(PO₂)分布。(数据来源:Kislyakov, Y. Y. 及 Ivanov, K. P.,《生物力学工程杂志》(J. Biomech. Eng.),第108卷,第28页,1986年。经许可引用。)
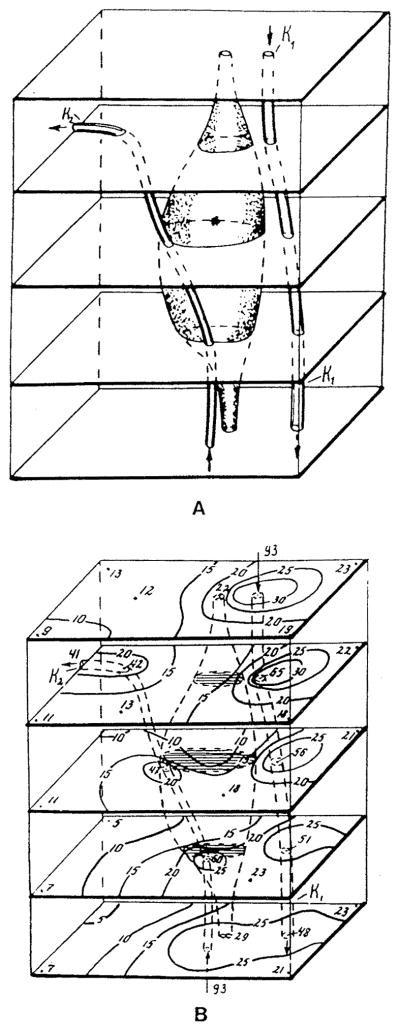
图30.(a)被两条毛细血管(K1和K2)包围的神经元;(b)横截面内的氧分压(PO₂)分布(细胞和毛细血管分别用阴影线和虚线标识)。截面中的曲线为等压线,数值表示氧分压水平(单位:托)。(数据来源:Ivanov, K. P.、Kislyakov, Y. Y. 及 Samoilov, M. O.,《微血管研究》(Microvasc. Res.),第18卷,第434页,1979年。经许可引用。)
在大多数氧气传输研究中,控制微分方程通过离散化方法(有限差分法或有限元法)进行数值求解。Bruley及其团队开发了一种概率方法,即通常所说的蒙特卡洛模拟(Monte Carlo simulation)¹³ˌ¹⁹¹。作者认为,与离散化方法相比,蒙特卡洛方法具有一定优势,尤其适用于几何结构复杂的问题;但目前该方法仅应用于简化的几何模型,其在更贴近实际的问题中的适用性仍有待验证。
有实验证据表明,脑循环中存在显著的毛细血管前氧损失。为将毛细血管前与毛细血管后微循环中的氧气传输纳入考量,Sharan等人¹⁶⁷对Roth与Wade¹⁴⁷提出的房室模型进行了改进,并将其应用于大脑氧气传输研究。该模型包含11个血管房室和1个组织房室,小动脉与小静脉的传输系数根据Popel与Gross¹³⁵的模型计算得出。模型中还纳入了大动脉与大静脉之间的逆流扩散分流,但结果显示这种分流的影响并不显著。研究人员利用绵羊和羔羊大脑的特性参数,针对不同类型的缺氧(低氧性缺氧、一氧化碳性缺氧和贫血性缺氧)进行了计算。
D. 肺
从某种意义上说,肺毛细血管中氧气的结合问题,与其他组织中氧气的释放问题恰好相反。因此,描述肺毛细血管中氧气传输的方程,与前文所述的其他组织中的传输方程相似。但二者存在一些重要差异:首先,肺毛细血管更准确的描述是“狭缝”而非“圆形管道”;其次,毛细血管中的血液与肺泡中的空气被一层膜分隔,该膜对氧气传输的阻力必须纳入考量;第三,毛细血管中二氧化碳浓度的变化,会通过玻尔效应(Bohr effect)和霍尔丹效应(Haldane effect)与氧气传输相互影响。因此,若要深入理解氧气传输过程,需对氧气和二氧化碳的传输进行同步分析。Weibel¹⁸⁶总结了肺内氧气交换涉及的机制;Roughton与Forster¹⁴⁹在其经典研究中提出了肺毛细血管传输的分析方法;Ulanowicz与Frazier¹⁷⁹则考虑了血红蛋白溶液中涉及氧气和二氧化碳的五个主要反应,并研究了氧气在静止血红蛋白平面层中的一维扩散;Hill等人⁶⁵在肺交换房室模型中采用了类似的研究思路。
Singh等人¹⁷¹构建了一个“狭缝状毛细血管通过平面壁交换氧气和二氧化碳”的模型。他们推导了氧气、二氧化碳、血红蛋白(Hb)、氧合血红蛋白(HbO₂)和碳酸血红蛋白(HbCO₂)的五个平衡方程,并对该问题进行了量级分析。这些方程描述了物质沿毛细血管的对流、物质间的化学反应,以及所有物质跨毛细血管的扩散过程,因此模型中纳入了氧气和二氧化碳的易化传输(facilitated transport)。随后,这些研究者在一系列文献中进一步应用了上述控制方程:包括给出该问题的数值解¹⁶²、纳入毛细血管轴向扩散¹⁶³与肺膜阻力¹⁶⁵,以及考虑非稳态过程¹⁶⁴。然而,描述氧气-二氧化碳-血红蛋白反应的方程¹⁷¹似乎基于一个假设——氧气和二氧化碳竞争血红蛋白分子上的相同结合位点,这使得这些方程与其他肺交换研究者所采用的描述方式存在显著差异。目前文献中尚未对这一差异进行批判性讨论,也无法明确文献162-165、171中的结果会受到模型推导假设怎样的影响。
E. 动脉壁
大动脉壁的氧气供应来自两个来源:一是血管腔,二是位于外膜(adventitia)和中膜(media)外层的特殊循环——血管滋养管(vasa vasorum)。动脉壁内层(内膜(intima)以及大部分中膜,甚至全部中膜)无血管分布;小动脉的整个管壁均无血管。动脉壁缺氧与动脉粥样硬化(atherosclerosis)相关,这一关联推动了动脉壁氧气传输的研究。动脉壁氧气传输的理论研究旨在深入理解“血管腔内血流模式”与“管壁内氧气分布”之间的复杂关系。Goldstick与Dobrin⁴⁷近期发表了关于动脉壁氧气传输的综述。
Back⁶针对稳态流和脉动流,对血管腔和无血管管壁中的传输过程进行了解析估算。他为血液区域和无血管管壁分别建立了标准传输方程,并设定了氧气通量与氧张力连续的匹配条件,同时指定了“远离管壁的血流中”和“无血管区域外边界”的氧分压(PO₂)。利用兔腹主动脉的数据,他得出结论:血液中传输阻力约为管壁传输阻力的两倍。研究发现,脉动流仅影响血管腔附近的狭窄区域内的氧气浓度。已知在血流中,管壁附近会形成几微米厚的无细胞层(cell-free layer)或低细胞层(cell-depleted layer)。Schneiderman与Goldstick¹⁵⁶在考虑无细胞层的前提下,获得了该问题的数值解,并得出结论:血液相中的氧气梯度会显著延伸至无细胞层之外,因此主要传输阻力存在于流动的血液中。Schneiderman等人¹⁵⁸提出了更通用的解法,其中纳入了血流的脉动性。图31展示了人胸主动脉内的氧气分布,预测结果显示,血液中显著的氧分压梯度可延伸至距管壁100微米处,而脉动性对氧气交换几乎无影响。类似模型还被用于分析“通过氧气微电极测得的在体与体外氧分压分布实验数据”(Buerk与Goldstick¹⁴)。该模型的扩展研究则涉及病变血管中的氧气传输问题(Back等人⁷;Schneiderman等人¹⁵⁷)以及一氧化碳性缺氧的影响(Schneiderman与Goldstick¹⁵⁵)。
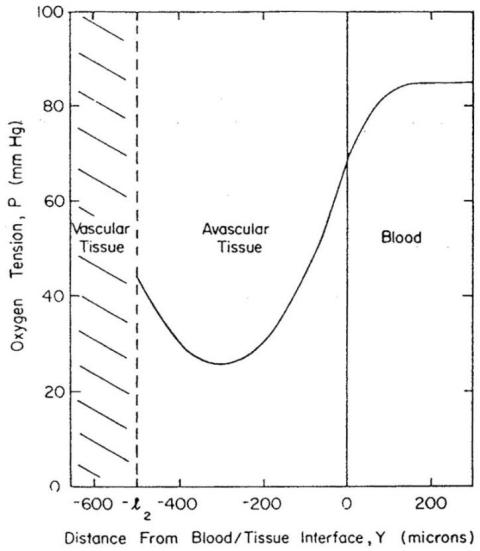
图31.人胸主动脉内稳态流下的氧分压(PO₂)分布。脉动流的时间平均分布与此差异极小,几乎无法察觉。氧气传输的主要阻力存在于流动的血液中。(数据来源:Schneiderman, G.、Mockros, L. F. 及 Goldstick, T. K.,《生物力学杂志》(J. Biomech.),第15卷,第849页,1982年。经许可引用。)
F. 皮肤
皮肤微循环具有非常特殊的结构:毛细血管形成伸向皮肤表面的袢状结构(capillary loops)。除氧气传输外,热量传输也是皮肤微循环的重要功能。Grossmann⁵⁴构建了皮肤微循环单元模型(图32a),该模型考虑了毛细血管内的扩散过程,还纳入了热传输方程;由于氧合血红蛋白解离曲线具有温度依赖性,质量传输方程与热传输方程相互耦合。图32b展示了“穿过毛细血管袢的横截面”内的氧分压(PO₂)分布实例。研究中还考虑了皮肤表面的加热与冷却,以及不同的氧气环境条件。该模型还被用于研究时间依赖型状态(Grossmann与Winkler⁵⁵)。
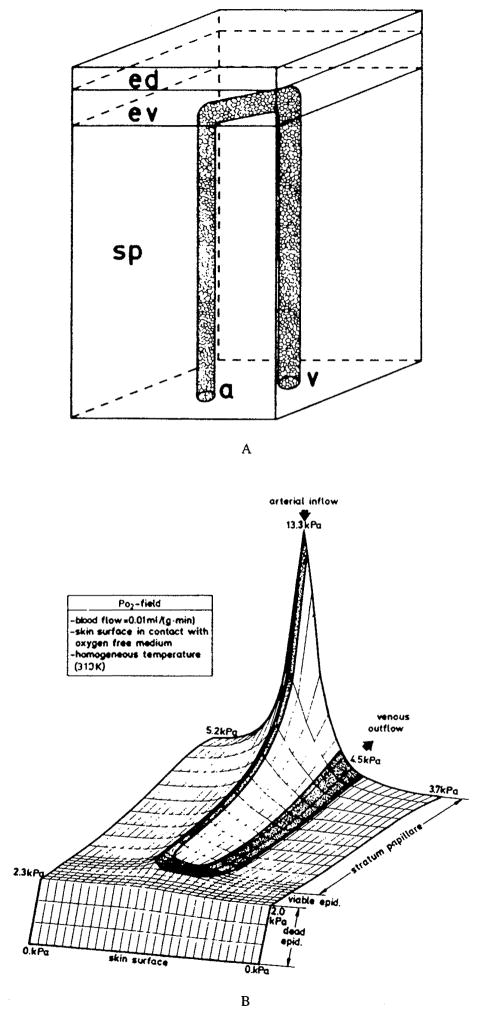
图32.(a)皮肤微循环单元(ed:死亡表皮;ev:存活表皮;sp:乳头状层;a:动脉流入端;v:静脉流出端);(b)穿过毛细血管袢的微循环单元横截面内的氧分压(PO₂)分布。血流处于静息状态,皮肤表面接触无氧介质,整体温度维持在37°C。(数据来源:Grossmann, U.,《数学生物科学》(Math. Biosci.),第61卷,第205页,1982年。经许可引用。)
G. 其他器官
研究人员还对其他多种组织和器官的氧气传输进行了理论研究:计算了颈动脉体(Grossmann等人⁵³;Degner与Acker²⁶)、眼睛的视网膜(Friedland⁴¹)与角膜(Lin¹⁰⁹)以及神经(Lagerlund与Low¹⁰⁵)中的氧分压(PO₂)分布;此外,房室模型还被应用于肠道(Granger与Shepherd⁴⁸;Granger与Granger⁴⁹)、胎儿循环(Huikeshoven等人⁷⁸)和胎盘循环(Hill等人⁶⁶)的氧气传输分析。
第七章 疾病状态下的氧气传输模型:镰状细胞贫血
在镰状细胞贫血(sickle cell anemia)中,氧气通过一系列血液流变学(hemorheological)和传输过程发挥关键作用。当氧气在毛细血管中释放时,红细胞会变硬,导致血液黏度升高,进而使血流速度降低;这反过来会限制氧气输送,进一步减缓血流,最终导致循环阻塞。因此,在理论模型中,需将氧气传输问题与“毛细血管内红细胞运动的力学问题”相结合,使力学过程依赖于氧气水平。Lomen与Gross¹¹¹以及Berger与King⁹ˌ¹⁰通过将克罗格模型与Lighthill和Fitz-Gerald的毛细血管流动模型相结合,深入研究了这一问题。近期,Granger与Shepherd⁴⁸提出的房室模型被进一步扩展,用于描述镰状细胞疾病中的微循环氧气输送(Vayo等人¹⁸³)。
第八章 结论与展望
目前已构建的数学模型已纳入氧气传输的重要特征:解剖学上真实的毛细血管网络几何结构、毛细血管内传输阻力、肌红蛋白对氧气扩散的促进作用,以及线粒体分布不均导致的细胞内异质性。然而,尽管研究正朝着这一方向推进,尚无任何一种组织的模型能涵盖所有被认为对该组织重要的特征。理论研究的主体仍是“旨在开发新模型或推导现有模型数学解的方法学研究”,而针对特定组织(尤其是骨骼肌和大脑以外的组织)的应用研究则相对较少,且鲜有定论。目前,所有氧气传输模型(包括克罗格模型)均未通过实验数据的严格验证,其主要原因在于:缺乏具有足够空间分辨率的“在体氧张力与血红蛋白饱和度精确测量数据”,而这种分辨率是验证分布式传输模型所必需的。不过,随着新型微循环技术的出现,此类数据已开始逐步积累,因此,通过直接实验验证数学模型的可行性将首次成为可能。
仅在十年前,“氧气从细胞输送到耗氧部位”的过程描述,与克罗格提出的理论在定性上仍无显著差异。而在过去十年中,克罗格关于“组织内从毛细血管向外呈径向氧分压梯度”的观点发生了巨大转变,甚至近乎完全逆转。事实上,目前有观点认为:从血红蛋白到线粒体的路径中,主要的氧分压梯度并非存在于组织中,而是存在于血管内部。这些新观点需要进一步的实验验证和新的理论发展;但如果这些观点成立,那么我们对“组织氧气传输”的大部分认知都将需要重新评估。
转载本文请联系原作者获取授权,同时请注明本文来自孙学军科学网博客。
链接地址:https://wap.sciencenet.cn/blog-41174-1500012.html?mobile=1
收藏

