THEORY OF OXYGEN TRANSPORT TO TISSUE - PMC

四、组织中氧转运模型

A. 均质组织中的扩散

均质组织中的氧扩散遵循反应 - 扩散方程：

式中，Pt​为组织氧张力，Dt​为扩散系数，αt​为溶解度系数，M为氧气被消耗的不可逆化学反应速率。需注意的是，此情况与 “氧气与血红蛋白、肌红蛋白的可逆化学反应” 存在显著差异。化学反应速率可作为Pt​的函数，目前常用的氧消耗模型包括：

（a）零级动力学模型：

其中，Pm​为 “反应速率达到最大值一半时的氧分压（PO2​​）”。当Pm​→0时，米氏动力学模型趋近于零级动力学模型，即M→M0​；当氧张力较小时（Pt​≪Pm​），米氏动力学模型趋近于一级动力学模型。混合动力学模型（c）可视为米氏动力学模型（d）的分段线性近似。

基于 “氧气代谢的双细胞色素模型” 假说，研究人员提出了米氏动力学模型的推广形式 [125]：

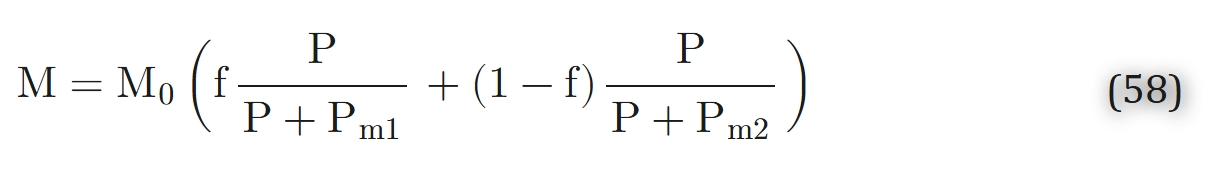
式中，0≤f≤1，Pm1​与Pm2​均为常数。

对于 “占据x≥0空间的半无限大组织层”，在稳态条件下可轻松求解公式 53。若采用零级动力学模型，其解为：

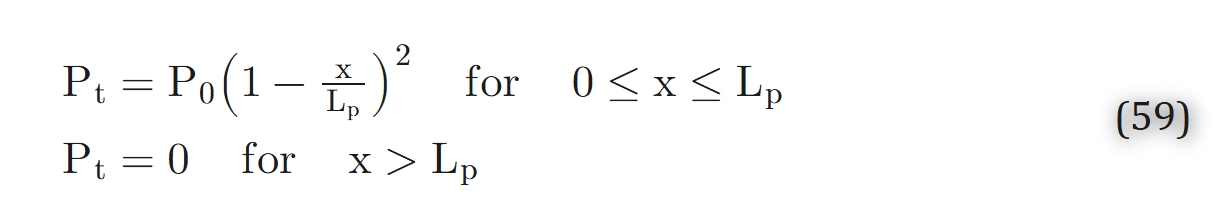
其中，Lp​=M0​2Dt​αt​P0​​​为 “氧张力降至零的渗透深度”。希尔（Hill）[64] 还给出了公式 53 在平面和柱形几何模型下的其他多种解。若采用一级动力学模型，其解为：

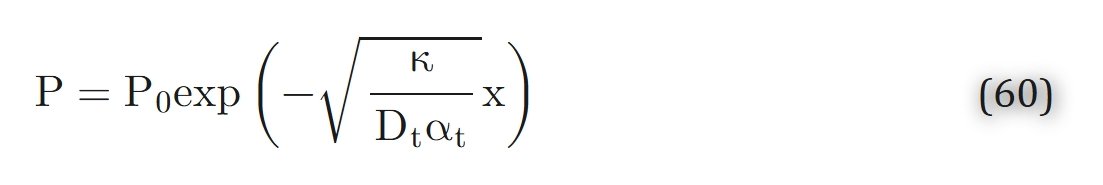
因此，与零级动力学模型不同，在一级模型中组织内各处的氧分压（PO2​​）均为正值，即氧分子可从边界无限深入组织内部。混合动力学模型和米氏动力学模型也会呈现类似特征 —— 因为当Pt​较小时，它们的行为与一级动力学模型一致。

通常可对公式 53 进行一次积分：

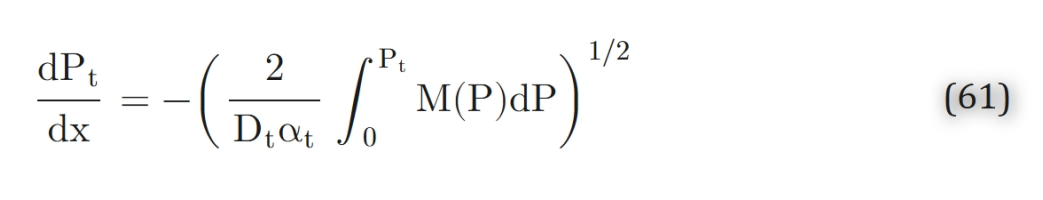
结合边界条件Pt​(0)=P0​对公式 61 积分，可得到公式 53 的隐式解：

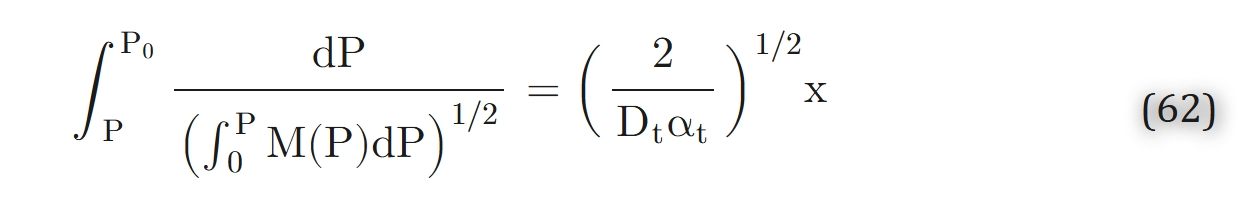
对于某些M(P)函数（如多项式形式的M(P)），可通过解析方法计算公式 62 中的积分，从而得到封闭形式的解。而对于米氏动力学模型，公式 62 中的外层积分无法通过解析方法计算，因此必须采用数值积分

希尔（Hill）[64] 还研究了稳态和非稳态条件下，平面和柱形组织层中氧气与乳酸的同步扩散过程。此外，研究人员还得到了其他几何模型下组织扩散的解。

零级动力学模型对应的非稳态问题求解存在数学和计算上的难点 —— 这是因为存在 “分隔氧分压为零与非零区域的移动边界”，而确定该边界的运动规律是求解过程的一部分 [24,32,42]。在数学文献中，这类含移动边界的问题被称为 “斯特凡问题（Stefan problems）”。

B.非均质组织中的扩散

上一节的模型假设组织在空间上是均质的，但实际上组织由细胞和细胞外间隙组成。此外，组织内部还存在异质性（如线粒体对氧气的离散消耗导致的异质性），这些异质性可能会影响组织内的氧分布。

首先，我们考虑 “细胞内外扩散差异” 导致的细胞水平组织异质性。希尔（Hill）[64] 已对该问题进行了定性分析。Tai 与 Chang [176] 提出了 “由具有不同扩散特性的平面层组成的组织模型”（图 11）。扩散系数与溶解度系数的乘积通常被称为渗透率或克罗格系数（Krogh coefficient），即K=Dα。该模型假设：细胞内和细胞外介质的渗透率可分别用Kc​和Ke​表征，且细胞以恒定速率m（零级动力学）消耗氧气。若ϕe​为细胞外物质的体积分数，则组织的体积平均氧消耗率为M=(1−ϕe​)m。“非均质介质层的有效渗透率” 定义如下：对于一个 “消耗率均匀为M的均质介质”，若其边界处的氧分压差值与非均质介质相同，且对应边界处的氧通量也相等，则该均质介质的渗透率即为非均质介质层的有效渗透率。在该模型中，细胞层与细胞外层层叠方式分为 “平行” 和 “串联” 两种，其对应的有效渗透率分别为： 

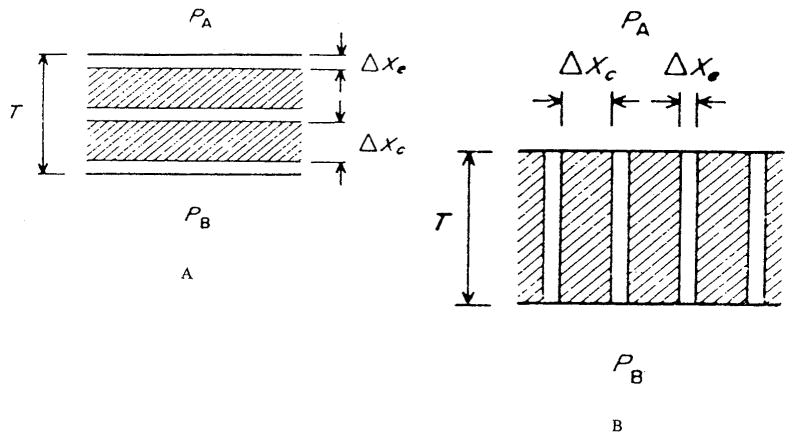
 图11.异质组织模型的定义示意图：（a）串联模型；（b）并联模型。（来源：Tai, R. C. 与 Chang, H. -K.，《理论生物学杂志》，第43卷，第265页，1974年。已获转载许可。）

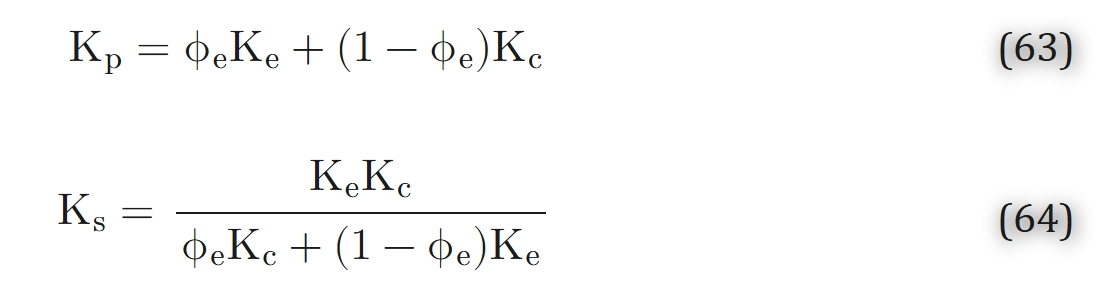
式（63）和式（64）可由Tai与Chang[176]提出的方程推导得出。需注意，Kp（并联模型渗透率）和Ks（串联模型渗透率）与组织切片厚度无关，仅取决于各区域渗透率及细胞外间隙体积分数。通过直接比较可证明，Kp \geq Ks。Tai与Chang[176]还对早期模型[67]进行了拓展，以分析“在距组织边界特定距离处，细胞呼吸速率未达最大值”的情况。该呼吸速率的确定，需求解“零级动力学下球形或椭球形细胞内氧气分布”问题（此时细胞中心区域处于缺氧状态）。Stroeve[174]进一步推进了相关研究：他通过解析法求解了“零级或一级动力学下球形细胞内部及周围的扩散方程”，随后对结果进行体积平均。其研究方法借鉴了麦克斯韦（Maxwell）推导异质材料传输特性的经典方法。对于零级动力学，他得到以下表达式： 研究表明，对于其他几何结构的介质，其渗透率的上下边界分别为串联模型与并联模型的渗透率（即式63和式64）；具体而言，满足Ks< K₀< Kp。若通过

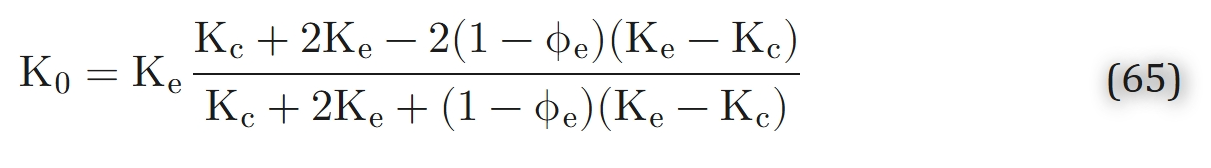
实验测得有效渗透率，且已知细胞外介质的渗透率，则可利用式（63）至式（65）估算细胞渗透率Kc。Stroeve[174]利用猫大脑皮层的实验数据，通过上述三个模型（式63至式65）估算了Ke/Kc（细胞外介质渗透率与细胞渗透率的比值）。结果显示，Kc（细胞渗透率）的预测值是Ke（细胞外介质渗透率）的数倍，这表明氧气扩散的阻力主要集中在细胞内部。此后，研究人员针对一级动力学（式55）和混合动力学（式56）也得到了类似表达式[184]。在细胞内部，氧气几乎完全在线粒体中被消耗。因此，从理论上讲，细胞内氧分压（PO2）的分布可能存在显著异质性：线粒体周围的氧分压降幅较大，而胞质其余区域的氧分压分布则相对平缓。然而，Clark等人提出了极具说服力的观点，认为线粒体周围的氧分压降幅不应超过百分之几托（torr，压强单位）。对于半径为Rm的球形线粒体，可通过求解“球坐标系下线粒体周围氧气分布的扩散方程”轻松得到上述估算结果：

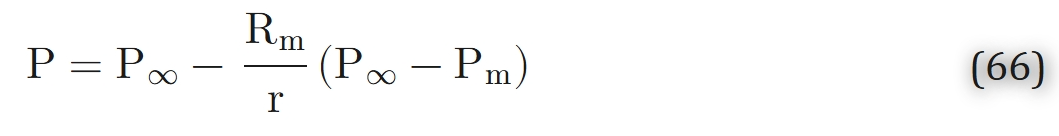
式中，P_∞为细胞内远离线粒体表面处的氧分压，Pm为线粒体表面的氧分压。此时，线粒体表面的氧气通量j满足j = K(P_∞/Pm)/Rm，其中K为胞质的氧气渗透率。另一方面，在稳态条件下，氧气通量与线粒体表面积的乘积等于线粒体消耗的氧气量，即：

式中，Vm=4\pi Rm^3/3$为线粒体体积，m_m为单位线粒体体积的氧气消耗速率。将式（66）与式（67）联立，经简单代数运算可得：

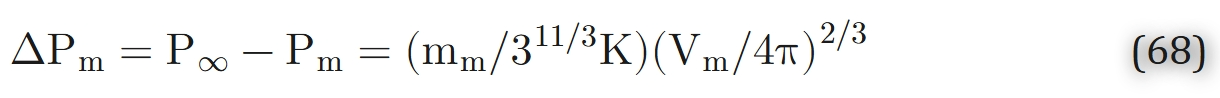
采用骨骼肌线粒体的典型参数[20]：m_m = 1.4·10⁻⁶ mol/ml/s, K = 2.13·10⁻¹⁴ mol/cm/s/torr,  V_m = 0.38 μm³,  代入式（68）可得ΔP_m = 0.04 torr。对于其他形状的线粒体，该估算值可能会有数量级为1的变化，但在所有情况下，其值均远低于1托。由此可见，组织中氧气扩散的阻力分布于细胞内部，而非集中在单个线粒体周围的狭窄区域内。换言之，若线粒体分布均匀，则氧气消耗的离散特性不会影响氧气分布的整体模式。然而，若线粒体存在显著的聚集现象，细胞内氧气的分布可能会发生改变。已有实验证据表明，线粒体可能在毛细血管和肌膜周围聚集。Mainwood与Rakusan[116]建立了一个“细胞内氧气扩散模型”，该模型同时考虑了三磷酸腺苷（ATP）或磷酸肌酸从线粒体向细胞其他区域的扩散过程。图12展示了该模型在“所有线粒体聚集于毛细血管3微米范围内”这一极端情况下的预测结果。这些计算表明，线粒体分布的异质性理论上可能影响细胞内的氧分压分布。但目前尚无基于系统收集的实验数据对该影响进行的定量分析。

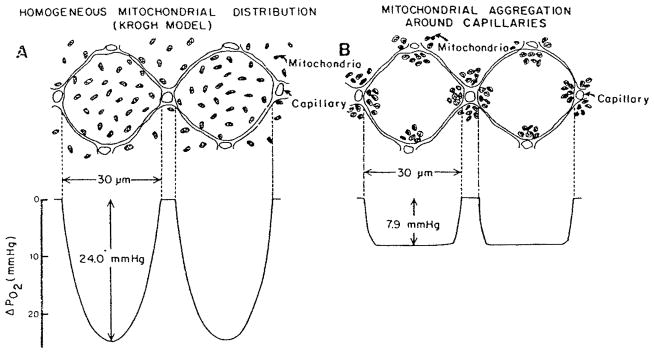
图12.细胞与毛细血管比例为1:1的圆柱形细胞内氧分压（PO₂）分布：（a）线粒体均匀分布；（b）线粒体聚集于毛细血管3微米范围内。（来源：Mainwood, G. W. 与 Rakusan, K.，《加拿大生理学与药理学杂志》，第60卷，第98页，1982年。已获转载许可。）

朗缪尔（Longmuir）[112]提出了一种与现有认知截然不同的细胞内氧转运观点。他认为，氧气会沿着高溶解度通道从血液转运至线粒体，而内质网可能起到氧气通道的作用。由于胞质中氧气溶解度较低，其内部几乎不含氧气。然而，这一假说的理论验证与实验验证仍有待开展。

转载本文请联系原作者获取授权，同时请注明本文来自孙学军科学网博客。

链接地址：https://wap.sciencenet.cn/blog-41174-1499977.html?mobile=1

收藏

分享