文章亮点介绍

近日，南京大学戴万阳教授在随机微分博弈与带跳正倒向偶合随机偏微分方程及人工智能AlphaGo模型研究取得新突破，在随机微分博弈决策与随机偏微分方程解的关系上发现关联、在带跳正倒向偶合随机偏微分方程的体系上实现了归一化并发展了方法证明其四元组解的存在唯一性。本文章已发表于MDPI Mathematics 期刊。

文章介绍

研究背景及目的

本文主要针对能源系统资源共享共赢博弈与著名人工智能AlphaGo动力系统中输赢生存博弈、量子均值场与量子计算系统中的决策均衡、3D空间人工智能系统噪声加密与噪声解码与算法而展开的归一化模型体系的研究与应用。同时，本文也针对求解动态博弈决策均衡方程的体系展开了研究。

模型及结果分析

本文针对共赢非零和博弈与生存零和博弈发展了相关的体系模型，并发现了与带跳随机偏微分方程解的关系，在随机微分博弈决策与随机偏微分方程解的关系上发现关联、在带跳正倒向耦合随机偏微分方程的体系上实现了归一化并发展了方法证明其四元组解的存在唯一性。本研究可用于能源博弈与著名人工智能AlphaGo动力系统模型的建立、也可用于量子均值场与量子计算的研究。带跳正倒向耦合随机偏微分方程归一化体系对发展高维平面和流型上噪声加密与噪声解码人工智能系统 (Encode-Decode Transformer) 会产生推动作用，尤其是对发展3D空间人工智能的系统与算法会产生基础性的作用，而相关噪声可以设定为高斯噪声，也可以设定为非高斯噪声，拓广了现存的实际使用。另外，如下图所示，本文中所发展的体系可用于多种实际系统输入控制与路由平衡，其相应的决策方案可通过有关的带跳的随机偏微分方程的解求得或学习训练出。

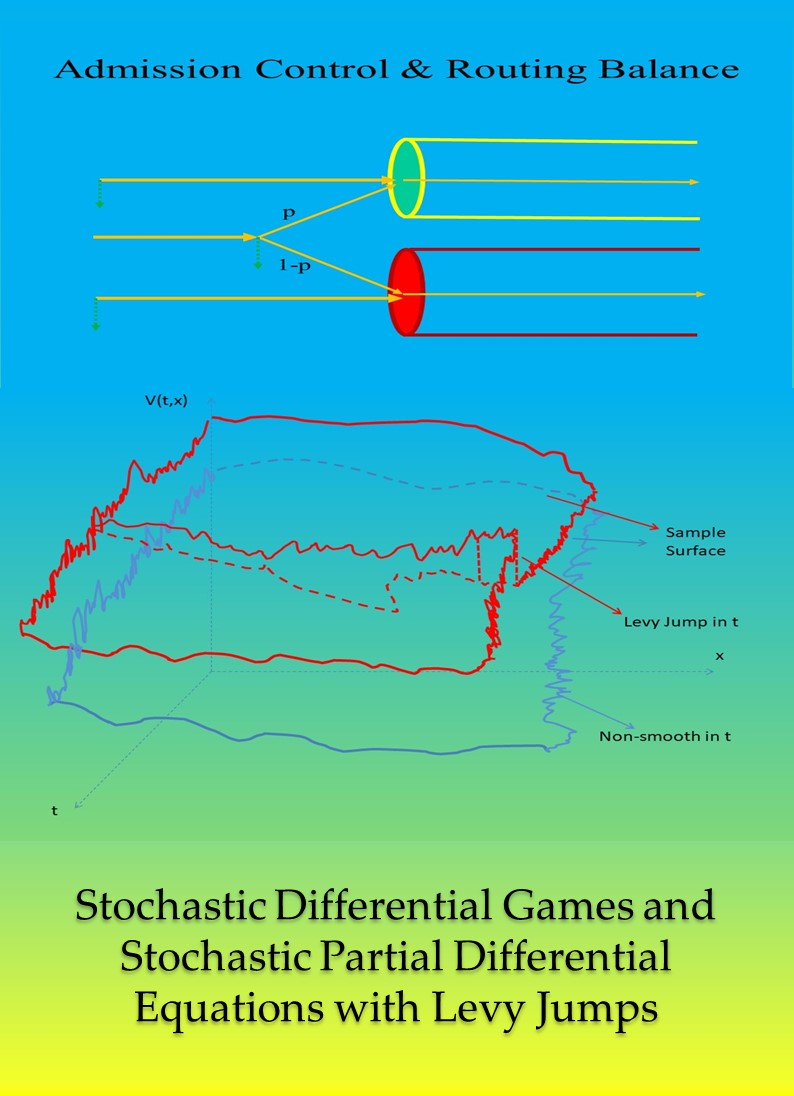
上图是一简单网络的输入与路由控制示意图，下图是带跳随机偏微分方程解的样本曲面示意图。

讨论与总结

本文在随机微分博弈决策与随机偏微分方程解的关系上发现关联、在带跳正倒向耦合随机偏微分方程的体系上实现了归一化并发展了方法证明其四元组解的存在唯一性。所得结果成功地用于刻画能源系统资源共享共赢博弈与著名人工智能AlphaGo动力系统中输赢生存博弈、为量子均值场博弈与量子计算系统中的决策均衡提供了归一化的体系，也为进一步发展3D空间人工智能算法提供了基础。

作者介绍

戴万阳 教授

南京大学数学学院

研究领域：量子计算与量子人工智能、随机网络与反射扩散逼近、随机最优控制与微分博弈，随机 (常/偏) 微分方程，过程统计学与数据科学，机器学习与卷积神经网络，信息技术与通信网络。

原文出自 Mathematics 期刊：https://www.mdpi.com/2227-7390/12/18/2891

期刊主页：https://www.mdpi.com/journal/mathematics

Mathematics 期刊介绍

主编：Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK

期刊主题涵盖纯数学和应用数学所有领域，重点发表代数、几何和拓扑、函数插值、差分和微分方程、计算和应用数学、概率与统计、数学物理、动力系统、工程数学、数学和计算机科学、数学生物学、网络科学、金融数学、以及模糊集、系统和决策等相关领域的文章。现已被SCIE (Web of Science)、Scopus等重要数据库收录，JCR Category Rank: 21/489 (Q1)。

2023 Impact Factor：2.3

2023 CiteScore：4.0 

Time to First Decision：17.1 Days

Acceptance to Publication：2.6 Days