博文
爱因斯坦与玻尔世纪之争的焦点是要否定《随机过程》研究方法
||
爱因斯坦与玻尔世纪之争的核心问题,就是坚决反对玻尔用概率来描述单个粒子运动状态的研究方法,而当今《随机过程》教科书所使用的研究方法,恰恰就是爱因斯坦坚决反对的“用概率描述单个粒子运动状态”的研究方法。
1926年,薛定谔建立了《量子力学》描述微观粒子行为的波动方程(也称薛定谔方程),以玻尔为代表的量子力学哥本哈根学派在解释薛定谔方程中的波函数时,用概率来描述单个粒子的运动状态,遭到了爱因斯坦和薛定谔本人的强烈反对。
爱因斯坦认为概率只能描述处于相同环境中为数众多而又相互独立的粒子全体,而不能描述单个粒子的运动状态,因为单个粒子的运动状态必须是决定性的,不能是统计性的。单个粒子的运动状态只能像牛顿力学一样,用确定性的时间函数来描述。玻尔用概率描述单个粒子的运动状态,就如同用温度描述单个分子的运动状态一样荒谬。
物理学是一门实验科学,所有的物理学理论最终必须要与实验相符合。但是受科学实验条件和水平的限制,人们无法对微观粒子的空间位置和瞬时速度进行准确测量,因此双方都不能借助于物理学实验结果来验证自己的方法或推翻对方的方法,只能使用理想实验来证明或反驳对方方法中的逻辑错误。
1935年,薛定谔提出了“薛定谔猫”的理想实验,充分暴露出了玻尔研究方法的逻辑悖论,为爱因斯坦驳斥玻尔的概率解释提供了重要的逻辑武器。
但是,“理想实验”只是一种逻辑推理的思维过程,它的作用仅限于逻辑上的证明与反驳,不能用来作为检验认识正确与否的标准,因此,“理想实验”存在较大的局限性。相反,由“理想实验”得出的任何推论,最终必须要由观察或实验的结果来检验。
此外,由于微观粒子具有波粒二象性,使双方的争论从最初的物理学领域进入到后来的哲学领域,引发了关于物理实在、因果关系和观测本质的长期争论,许多物理学家和哲学家都卷入其中,谁也无法驳倒对方,导致这一论战至今无法结束,争论的问题至今也没有最后的定论,给其它学科的建立和发展带来严重的隐患和灾难。
例如,数学家们在研究和描述宏观世界的随机现象时,采用了玻尔的研究方法,在《随机过程》教科书中用概率来描述单个粒子的随机游走和布朗运动,维纳将爱因斯坦布朗运动扩散方程中的浓度当作单个布朗粒子位移的概率密度函数,给出了布朗粒子位移服从正态分布的布朗运动定义,由此推出了“布朗运动路径处处不可导(瞬时速度无穷大)”的著名论断。
令人遗憾的是,基于玻尔研究方法建立的《随机过程》理论,不仅与自然科学、工程技术和社会科学领域大量的科学事实不符,而且与《物理学》和《随机信号分析》理论矛盾冲突,无法正确描述宏观世界的随机运动现象及规律,为自然科学、工程技术和社会科学提供了错误的理论、方法及工具。
《数理金融学》基于《随机过程》布朗运动模型推导出的B-S期权定价公式由于从理论上解决了金融资产的定价问题,使金融市场获得了空前规模的发展,但是也造成了1987、1997和2007年的三次重大金融危机。被誉为“中国金融数学开创者”的彭实戈院士在《中国基础研究发展报告(2019年)》第二章中国数学前沿进展中明确指出:B-S期权定价公式是造成以前历次重大金融危机的关键性原因。畅销书《黑天鹅》作者塔勒布(Taleb)在《金融时报》上发表了题为“破坏市场的伪科学”专栏文章,痛斥B-S期权定价公式获得诺贝尔奖不仅是对科学的侮辱,而且使金融体系一直面临崩溃的风险。
值得庆幸的是,布朗粒子是宏观粒子,其运动状态遵循牛顿力学,人们有可能准确测量出布朗粒子的位移和瞬时速度,用科学实验方法对《随机过程》布朗运动理论进行实验检验,并在宏观世界结束爱因斯坦与玻尔之间的这场世纪之争。
2010年,美国得克萨斯大学的李统藏利用激光光镊技术首次实验测量到了悬浮布朗粒子的瞬时速度,实验结果表明:布朗运动瞬时速度为白噪声,直接颠覆了《随机过程》布朗运动理论中“布朗运动路径处处不可导(瞬时速度无穷大)”的著名论断,实验证明玻尔的研究方法无正确描述宏观粒子随机运动现象及规律,标志着爱因斯坦的研究方法在宏观世界战胜了玻尔,爱因斯坦在宏观领域大获全胜。
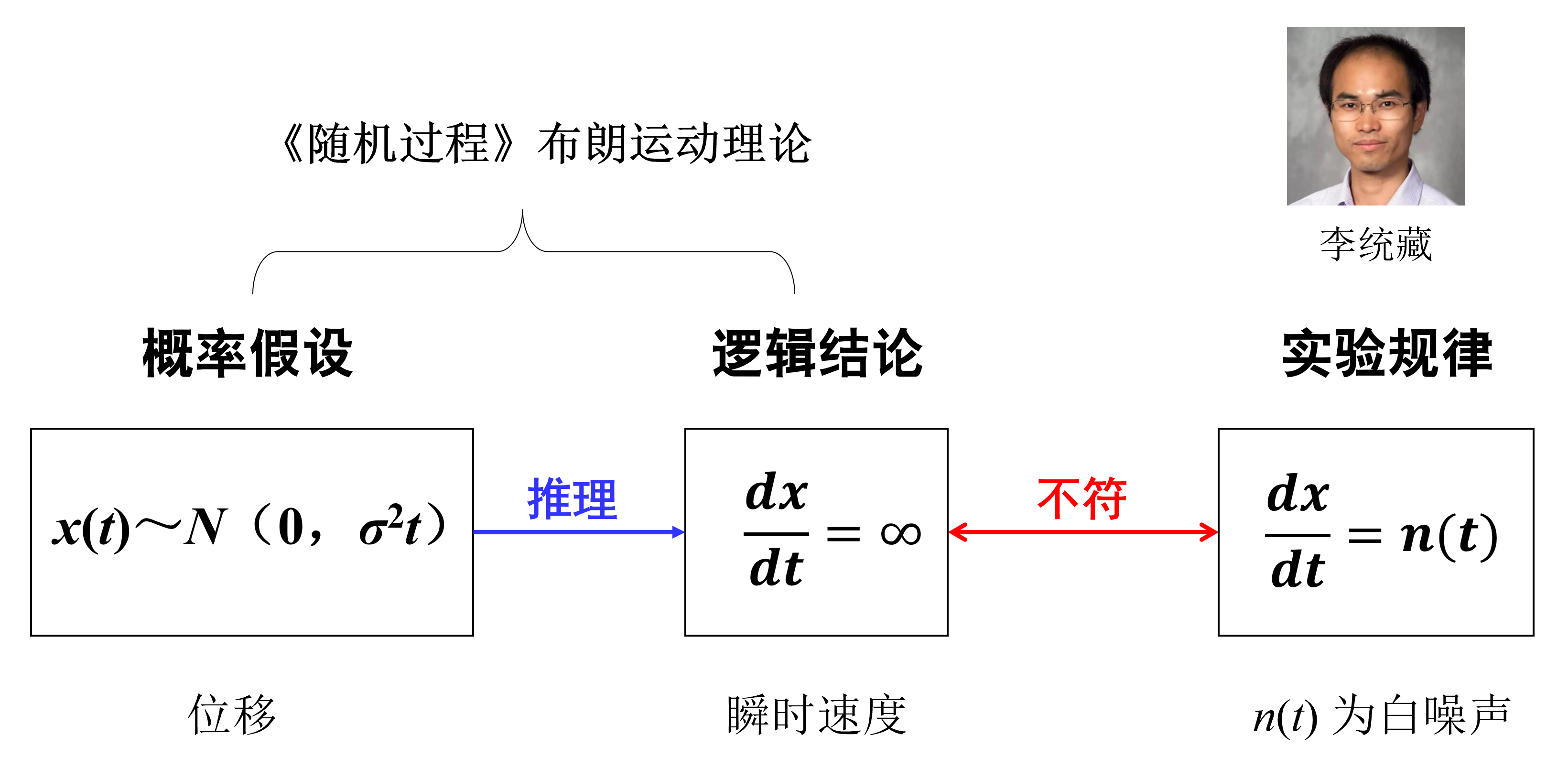
图1 《随机过程》布朗运动理论的实验检验
李统藏的实验结果不仅在宏观领域推翻了玻尔的研究方法,给爱因斯坦与玻尔的世纪之争在宏观世界画上句号,而且也颠覆了《随机过程》用概率描述单个宏观粒子运动状态的研究方法,这将迫使人类认识宏观世界随机运动的思维方式发生根本性的变革,导致《随机过程》研究方法发生重大范式转换。
《随机过程》教科书中基于玻尔研究方法建立的错误理论将会被基于爱因斯坦研究方法建立的新理论所取代,就像哥白尼“日心说”代替托勒密“地心说”一样,使人类对宏观世界随机现象的认识发生质的飞跃,引发一场深入持久的科学革命,为中国的数学学科进入世界一流水平前列提供了千载难逢的历史性发展机遇。
参考:
[1] Tongcang Li, S. Kheifets, D. Medellin, and M. G. Raizen. Measurement of the Instantaneous Velocity of a Brownian Particle[J]. Science, 2010(25):1673-1675.
https://www.science.org/doi/10.1126/science.1189403
[2] 教科书中两种对立冲突的布朗运动理论及实际应用效果
https://blog.sciencenet.cn/blog-3418723-1458326.html
[3] 为什么数学家对布朗运动的描述与物理学家矛盾冲突?
https://blog.sciencenet.cn/blog-3418723-1482773.html
https://wap.sciencenet.cn/blog-3418723-1484444.html
上一篇:薛定谔的猫暴露了《随机过程》研究方法的荒谬
下一篇:DeepSeek阐述李统藏布朗运动瞬时速度实验的意义