引用本文
满景涛, 曾志刚, 盛银, 来金钢. 基于ODE-PDE的大规模多智能体系统有限时间编队. 自动化学报, 2025, 51(3): 631−642 doi: 10.16383/j.aas.c240426
Man Jing-Tao, Zeng Zhi-Gang, Sheng Yin, Lai Jin-Gang. Finite-time formation of large-scale multi-agent systems based on an ODE-PDE approach. Acta Automatica Sinica, 2025, 51(3): 631−642 doi: 10.16383/j.aas.c240426
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240426
关键词
大规模异构多智能体系统,常微分−偏微分方程,实际有限时间编队,半马尔科夫切换拓扑,异步边界控制
摘要
现有基于偏微分方程(Partial differential equation, PDE)的多智能体系统(Multi-agent system, MAS)编队控制方法要求智能体必须是密集分布的, 为打破这一限制, 提出一种新的基于常微分−偏微分方程(Ordinary differential equation-partial differential equation, ODE-PDE)的分析方法, 以解决稀疏−密集混合分布的大规模异构MAS编队问题. 首先, 通过设计特定的通信协议, 并基于空间离散系统部分连续化方法, 将原始大量的异构MAS的ODE动力学模型转化为由一个PDE 和少数几个ODE耦合而成的ODE-PDE 模型. 为更符合实际复杂场景, 将拓扑权值规定为半马尔科夫切换的, 且稀疏分布和密集分布智能体遵循不一致的切换规则. 其次, 针对无时滞和有时滞两种情形, 设计两种异步边界控制策略, 利用Lyapunov方法得到保证误差系统实际有限时间稳定的充分条件, 并得到停息时间和稳定阈值的计算规则. 最后, 两个广义的数值仿真进一步验证了所提方法的有效性.
文章导读
近年来, 通信技术和人工智能的飞速发展推动了多智能体系统(Multi-agent system, MAS)控制理论在无人机集群、智能交通和微电网群等领域的广泛应用, 引起很多学者的重点关注[1–3]. 实际需求的日益多样化和工业产品的日益多元化导致MAS的规模不断扩大, 这给传统的基于常微分方程(Ordinary differential equation, ODE)的分析过程带来挑战. 当MAS规模较大时, 以ODE表示的MAS模型维数会急剧增高, 使相关的理论分析和控制器设计变得十分复杂, 控制效果也会相应下降[4]. 为解决这一问题, 一些学者提出基于偏微分方程(Partial differential equation, PDE)的方法用于大规模MAS的协同控制. 与ODE方法相比, PDE方法的主要优势在于仅用一个PDE就可以有效地表示大规模MAS的集体动力学, 且无论MAS的规模如何变化, 都能够始终保持恒定的分析复杂度和控制效果[5].
下面列举基于PDE方法的几个代表性结果. 假设智能体可以获得目标曲线的局部信息及其与最近邻居的相对位移, Wei等[6]将大量一阶智能体的集体动力学建模为扩散方程(一类典型PDE), 并通过Halanay不等式实现了其指数编队; 考虑无时滞和有时滞两种情形, Su等[7]研究了大规模移动二阶智能体的指数编队问题, 其动力学由二维或三维空间中的强阻尼波动方程(也是一类典型的PDE)描述. 在网络缺陷的背景下, Terushkin等[8]分别研究了非线性一阶智能体和二阶智能体在开环光滑曲线上的编队问题, 并设计相应的静态输出反馈控制器. 此外, 还有一些学者利用基于PDE的反步法研究了大规模MAS的编队控制问题[5, 9–10], 等等.
然而, 由于ODE模型向PDE模型转换的过程中存在精度损失, 导致PDE方法仅适用于有限空间内智能体足够多的场景, 即空间内的智能体必须密集分布才能保证模型足够精确, 这将大大限制PDE方法的适用性. 因为实际场景往往是复杂动态的, 很难保证所有智能体始终都呈密集分布, 很可能存在一部分密集分布、另一部分稀疏分布的情况. 例如, 假设有限区域内存在由几架无人机和上百辆无人车共同组成的大规模机−车编队, 当要求无人机在无人车上空分散盘旋时, 那么这几架无人机可以看作是稀疏分布的, 而上百辆无人车则可以看作是密集分布的. 针对这一问题, 本文提出一种基于ODE-PDE 的分析方法来研究MAS的编队问题, 该方法不仅适用于大规模MAS, 而且适用于一部分智能体密集分布、另一部分智能体稀疏分布的情形. 其核心思想是, 提出合理假设, 并通过特定的网络通信协议设计以及空间离散系统部分连续化的方法, 可以将MAS原始的ODE模型转化为ODE-PDE 模型, 然后利用ODE-PDE系统的分析方法和控制策略实现大规模稀疏−密集混合分布MAS的编队. 与现有PDE方法相比, 本文提出的ODE-PDE方法在普适性方面具备明显优势, 即不仅适用于大规模异构多智能体系统, 而且适用于智能体稀疏−密集混合分布的实际复杂场景.
从稳定时间的角度, 基于ODE方法的MAS有限时间协同控制问题得到了广泛而深入的研究, 因为有限时间控制比无限时域的控制更能满足实际MAS关于时效性的要求[11]. 然而, 基于PDE方法的MAS有限时间协同控制的研究结果非常有限[12–13], 尚处于研究的初始阶段. 为进一步丰富相关成果, 本文提出ODE-PDE方法研究MAS的实际有限时间编队问题. 与有限时间完全稳定不同的是, 实际有限时间稳定能够保证MAS状态和期望状态之间的误差在有限时间内收敛到一个特定的范围内, 而不必完全收敛到零[14–15]. 这种收敛性足以满足大多数MAS的实际控制要求, 例如, 在某些信号拦截任务中, 无人信号干扰器只要接近信号源, 就能够从信号源获取或干扰信号, 而无需完全到达该信号源的位置.
近年来, 一些学者将马尔科夫拓扑切换规则引入MAS中, 以刻画实际系统中由于非理想的外部环境和通信设备所导致的拓扑切换现象[16–17]. 然而, 马尔科夫切换过程规定模态的驻留时间只能服从指数分布, 且转换速率必须是常数, 这显然在实际应用中存在较大的局限性. 为放宽这一限制, 一些文献将半马尔科夫切换规则引入MAS中[18–20], 因为半马尔科夫过程允许驻留时间遵循非指数分布, 这在很大程度上增强了理论结果的普适性. 需要指出的是, 无论是马尔科夫切换拓扑还是半马尔科夫切换拓扑, 无论是同构MAS还是异构MAS, 现有的大多数文献都假设所有智能体的拓扑切换规则是一致的. 但是, 由于实际环境的复杂性和智能体类型的多样性, 很难确保所有智能体之间遵循相同的拓扑切换规则. 因此, 本文设计的网络通信协议假设异构MAS的拓扑服从于两个相互独立的半马尔科夫切换规则, 并规定控制策略的切换规则与通信拓扑的切换规则是异步的, 以更好地吻合实际拓扑切换情况.
面向大规模MAS, 考虑有时滞和无时滞两种情形, 本文的主要目标是提出一种基于ODE-PDE的分析方法, 通过边界控制实现MAS的实际有限时间编队. 本文的主要创新总结如下: 首先, 通过设计特殊的网络通信协议, 提出一种新的基于ODE-PDE的分析方法以应对大规模异构MAS的编队问题, 该方法允许智能体一部分密集分布、另一部分稀疏分布, 这在很大程度上放宽了已有PDE编队方法中“智能体必须密集分布”的限制, 因此, 与现有文献[5–10] 相比, 本文的主要结果普适性更强. 其次, 本文考虑MAS不一致半马尔科夫拓扑切换现象, 设计的通信协议中, 拓扑权值的切换服从两个相互独立的半马尔科夫过程. 相比于考虑恒定拓扑的文献[5–10]或者考虑一致拓扑切换的文献[16–20], 本文设计的拓扑切换规则更加广义、更符合实际拓扑切换情形. 此外, 本文规定控制策略切换规则与通信拓扑切换规则是异步的, 进一步提高了主要结果的合理性和实用性.
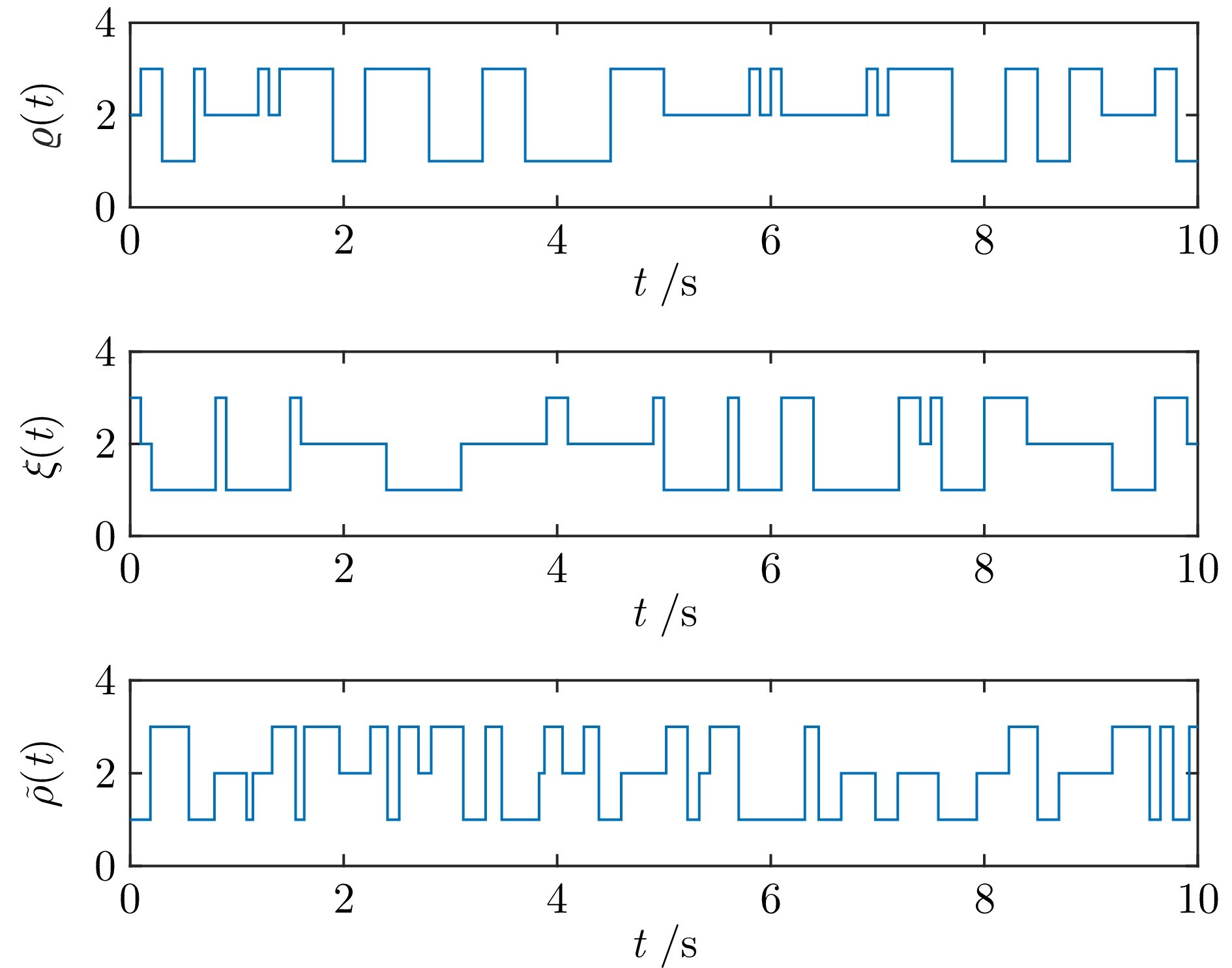
图 1 $\varrho(t)$, $\xi(t)$, $\tilde{\rho}(t)$的模态切换规则
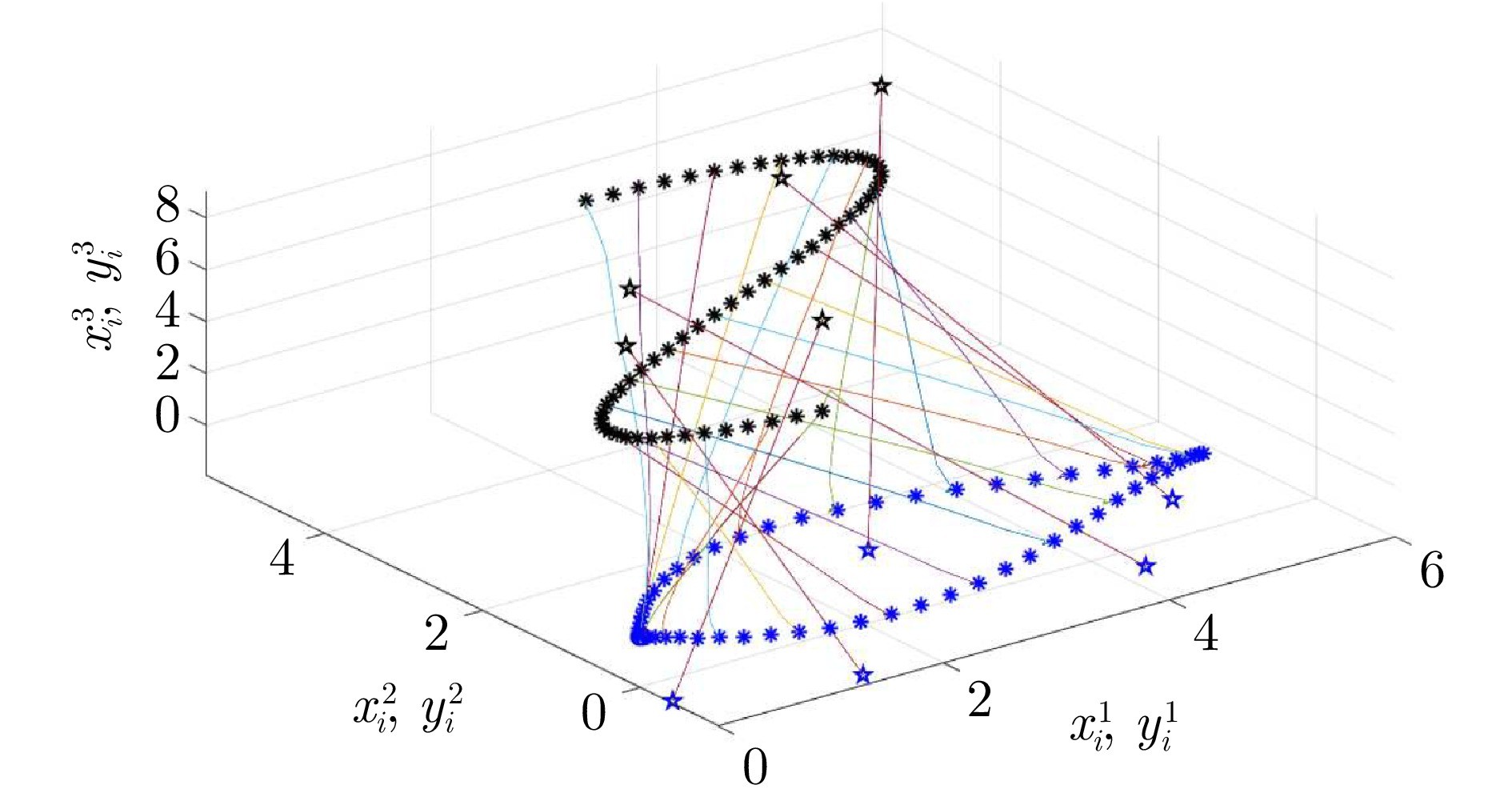
图 2 无时滞情形下MAS的运行轨迹
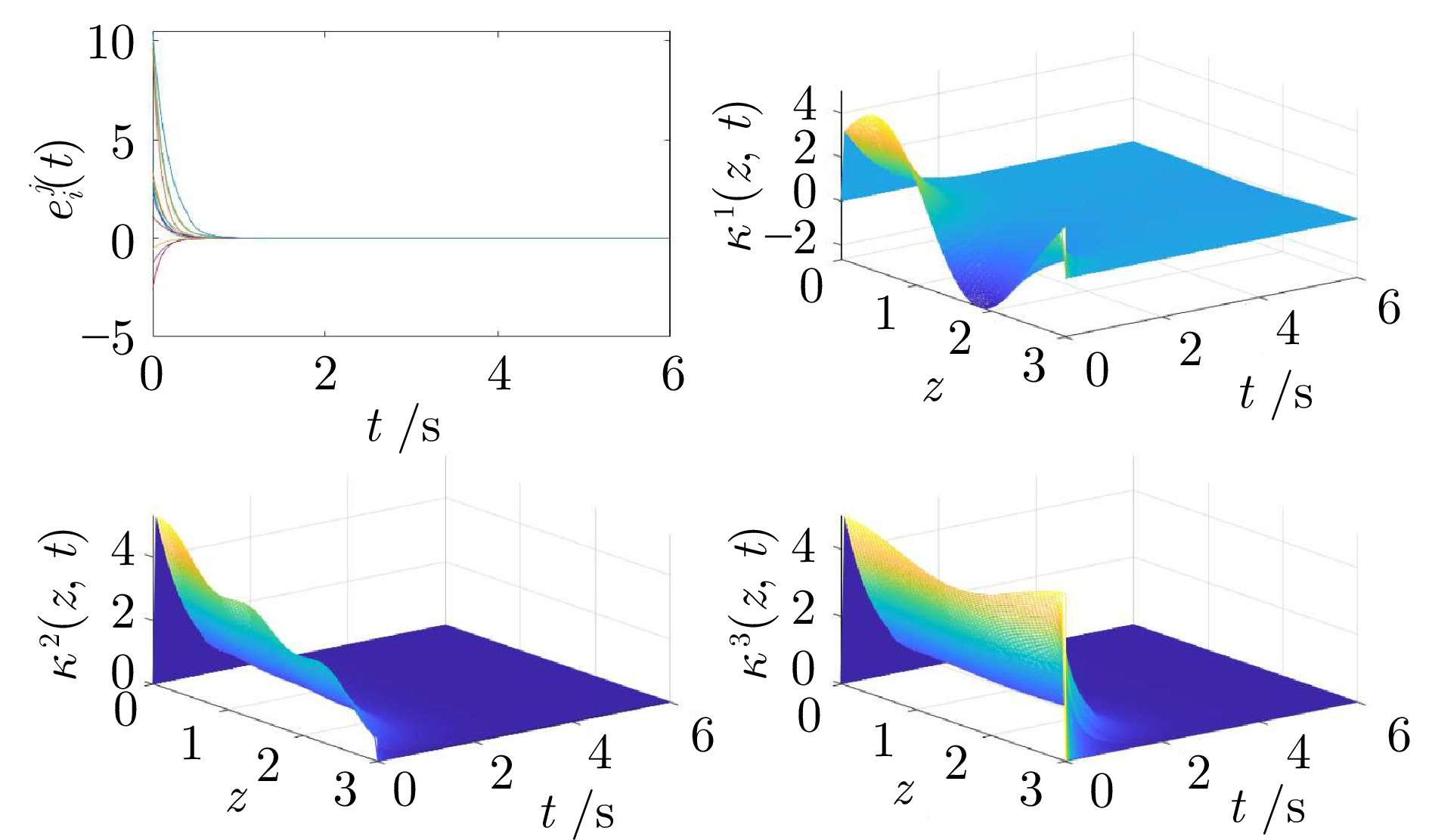
图 3 无时滞情形下单一空间维度上跟踪误差的状态轨迹
本文研究了大规模异构MAS的实际有限时间编队问题, 为此提出ODE-PDE分析方法, 相比于已有的PDE方法, 很大程度上放宽了理论结果的适用范围. 通过设计特殊的网络通信协议, 建立了MAS位置误差系统的ODE-PDE模型. 针对有时滞和无时滞情形, 设计了异步边界控制策略, 并得到相应的误差系统实际有限时间稳定准则. 最后, 两个数值仿真验证了设计的通信协议和边界控制策略的有效性. 未来的工作将聚焦于基于ODE-PDE方法的大规模MAS的固定时间编队控制问题.
作者简介
满景涛
华中科技大学人工智能与自动化学院博士研究生. 分别于2017年和2021年获得河南科技大学信息工程学院学士和硕士学位. 主要研究方向为随机系统、PDE系统和多智能体系统的控制策略设计与稳定性分析. E-mail: mjt546@163.com
曾志刚
华中科技大学人工智能与自动化学院教授. 2003年获得华中科技大学系统分析与集成专业博士学位. 主要研究方向为泛函微分方程理论和右不连续微分方程理论, 以及它们在神经网络动力学、忆阻系统和联想记忆中的应用. 本文通信作者. E-mail: zgzeng@hust.edu.cn
盛银
华中科技大学人工智能与自动化学院副教授. 2018年获得华中科技大学自动化学院系统分析与集成专业博士学位. 主要研究方向为神经网络, 忆阻系统, 模糊逻辑. E-mail: shengyin90@163.com
来金钢
华中科技大学人工智能与自动化学院教授. 主要研究方向为面向微电网、分布式可再生能源系统和信息物理社会系统的类脑智能和群体智能. E-mail: kklai@hust.edu.cn
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1483758.html?mobile=1
收藏