引用本文
王巍, 王珂, 黄自鑫, 王乐君, 穆朝絮. 执行器饱和的离散时间多智能体系统有限时域一致性控制. 自动化学报, 2025, 51(3): 617−630 doi: 10.16383/j.aas.c240446
Wang Wei, Wang Ke, Huang Zi-Xin, Wang Le-Jun, Mu Chao-Xu. Finite-horizon consensus control of discrete-time multi-agent systems with actuator saturation. Acta Automatica Sinica, 2025, 51(3): 617−630 doi: 10.16383/j.aas.c240446
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240446
关键词
有限时域一致性控制,执行器饱和,Q函数,模型无关,多智能体系统
摘要
针对执行器饱和的离散时间线性多智能体系统(Multi-agent systems, MASs)有限时域一致性控制问题, 将低增益反馈(Low gain feedback, LGF)方法与Q学习相结合, 提出采用后向时间迭代的模型无关控制方法. 首先, 将执行器饱和的有限时域一致性控制问题的求解转化为执行器饱和的单智能体有限时域最优控制问题的求解, 并证明可以通过求解修正的时变黎卡提方程 (Modified time-varying Riccati equation, MTVRE)实现有限时域最优控制. 随后, 引入时变参数化Q函数(Time-varying parameterized Q-function, TVPQF), 并提出基于Q学习的模型无关后向时间迭代算法, 可以更新低增益参数, 同时实现逼近求解MTVRE. 另外, 证明所提迭代求解算法得到的LGF控制矩阵收敛于MTVRE的最优解, 也可以实现全局有限时域一致性控制. 最后, 通过仿真实验结果验证了该方法的有效性.
文章导读
近年来, 多智能体系统(Multi-agent systems, MASs)分布式协同控制问题的研究取得了显著进展, 引发各个领域的广泛关注. 该研究范畴涵盖生物系统中的群体行为[1]、分布式传感器网络技术[2]和智能电网管理[3]等多个方面. 一致性问题作为支撑MASs分布式协同控制的基础问题, 不仅在理论层面具有深远的意义, 而且在实际应用中展现出巨大的价值. 一致性控制的根本挑战在于设计高效的一致性算法或协议, 旨在确保MASs的所有智能体能够逐步调整其状态或输出, 最终达到相同, 即实现智能体的一致性.
目前, MASs一致性控制的研究可以根据系统中领航者的数量划分为三种类别: 无领航者的一致性控制、领导−跟随一致性控制(一个领航者)以及包含多个领航者的一致性控制[4−6]. 到目前为止, MASs一致性控制的研究涵盖越来越复杂的智能体动态特性和通信网络拓扑, 包括但不限于线性[7]或非线性MASs[8]、整数阶[9]或分数阶模型[10]、固定[11]或时变拓扑[12]、输入延迟[13]、输入饱和[14]等. 在上述复杂情况下, 各种适当的控制算法被提出以实现一致性控制. 此外, 由于智能体的通信和计算资源有限, 基于事件触发的控制策略[15−16]被用于实现一致性控制, 有效减少了不必要的能源消耗. 然而, 这些研究成果只能实现渐近一致性控制, 即在理论上调节时间趋于无穷. 在实际应用中, 由于渐近一致性的收敛时间较长, 难以满足任务的时效性需求.
相比之下, 有限时域一致性被认为是一种更为理想的控制策略. 有限时域控制不仅能够缩短闭环系统的收敛时间, 还具备更好的鲁棒性和抗干扰能力[17]. 文献[18]提出一种分散模型预测控制方案, 实现了一阶MASs的有限时域状态一致性控制. 文献[19]采用分布式线性二次型博弈方法, 实现了离散时间二阶MASs的有限时域状态一致性控制. 此外, 文献[20−23]研究离散时变MASs的$ H_\infty $有限时域状态一致性控制问题. 上述有限时域状态一致性协议的设计通常假设智能体动力学模型已知[20−23], 或仅考虑简单的一阶[18]、二阶[19]系统. 然而, 一阶和二阶系统无法充分描述实际系统的动态特性, 而且在实际应用中, 系统模型信息通常是未知的或难以获取的. 传统的有限时域一致性协议在系统模型未知的情况下并不适用, 难以满足实际应用的需求.
自适应动态规划(Adaptive dynamic programming, ADP)[24]或强化学习(Reinforcement learning, RL)[25]能够利用仿生学习机制解决系统模型未知情况下的优化控制问题[26]. 其中, 学习状态−动作值函数的Q学习算法[27]为实现无模型最优控制提供了一种有效的解决方案. 近年来, 学者们利用ADP或RL算法, 通过逼近求解耦合的哈密顿−雅可比−贝尔曼(Hamilton-Jacobi-Bellman, HJB)方程, 以实现MASs的最优渐近一致性控制[7−8, 28−31]. 例如, 基于Q学习的算法已经应用于异构MASs[7−8, 28−29]和同构MASs[30−31]中, 用以实现模型无关的最优一致性控制. 然而, 这些文献主要关注无限时域一致性控制问题. 相比之下, 模型无关的有限时域一致性控制问题更具挑战性, 因为它需要在满足值函数终端约束条件的同时求解耦合的时变HJB方程.
为解决上述问题, 学者们开始研究基于ADP或RL的算法, 以逼近耦合的时变HJB方程的近似解, 从而实现MASs的有限时域最优一致性控制. 文献[32]提出一种基于局部动力学的离策略(Off-policy) RL算法, 实现线性MASs的有限时域最优状态一致性控制. 此外, 文献[33]针对非线性MASs提出基于ADP的有限时域鲁棒事件触发最优状态一致性控制方法. 然而, 上述一致性控制器的设计[32−33]仍然依赖于MASs的部分模型信息, 而在实际情况下, 这些系统模型信息通常难以获得.
为克服系统模型必须已知的问题, 文献[34]采用神经网络逼近每个智能体的动态特性, 然后在神经网络模型的基础上基于ADP设计有限时域最优编队控制方法. 然而, 这种方式会产生额外的计算开销, 并引入逼近误差, 从而影响ADP方法的有效性. 文献[35]提出一种基于积分RL算法和零和博弈理论的模型无关有限时域鲁棒最优编队包含控制方法.
由于在实际的MASs中普遍存在执行器饱和的问题, 如无人车电机的输出转矩受最大功率限制, 无人机的舵面受物理结构限制等, 饱和的非线性特性通常会导致系统性能下降, 甚至可能导致系统不稳定, 使得执行器饱和问题在理论和实践上都极具挑战性. 上述研究结果[32−35]无法确保在模型未知的情况下实现具有执行器饱和约束的MASs一致性控制.
为解决这一问题, 学者们提出基于RL或ADP的方法来处理执行器饱和的MASs模型无关一致性控制问题. 例如, 文献[36]提出一种新型的辨识−评价−执行结构, 结合粘性消失法, 解决了有输入约束MASs的领导−跟随最优一致性控制问题. 文献[37]提出一种离策略RL算法, 通过逼近求解具有非二次型代价函数的耦合HJB方程, 以实现一致性控制. 文献[31, 38−40]使用低增益反馈(Low gain feedback, LGF)方法[41]处理执行器饱和问题, 并结合ADP方法实现执行器饱和的MASs最优一致性控制. 然而, 这些基于ADP或RL的模型无关一致性控制方法主要解决的是存在执行器饱和的MASs无限时域一致性控制问题, 只能实现渐近一致性控制, 即理论调控时间趋于无穷. 文献[42]基于ADP研究具有对称或不对称输入约束条件的MASs事件驱动有限时域最优状态一致性控制问题, 但其控制器的设计要求已知系统的模型信息.
受上述分析的启发, 本文将LGF方法与Q学习相结合, 用以解决执行器饱和的离散时间线性MASs模型无关有限时域一致性控制问题. 首先, 根据LGF方法的思想, 推导得到修正的时变黎卡提方程(Modified time-varying Riccati equation, MTVRE). 求解MTVRE可以得到时变的低增益反馈律, 同时可以通过调整低增益参数来避免执行器饱和. 然后, 参考文献[43−44], 设计依赖于系统状态、控制输入和低增益参数的时变参数化Q函数(Time-varying parameterized Q-function, TVPQF). 在TVPQF的基础上, 提出一种基于Q学习后向时间迭代模型无关一致性控制方法, 该方法在不需要已知系统动力学模型的前提下, 能够逼近求解MTVRE, 从而实现离散时间MASs的有限时域一致性控制.
本文将LGF方法与Q学习相结合, 提出一种针对执行器饱和的模型无关有限时域一致性控制方法. 主要贡献如下: 设计一种依赖于智能体状态、控制输入和低增益参数的TVPQF. 基于TVPQF, LGF控制器的设计减少了对系统动力学模型的依赖; 提出一种可以迭代更新低增益参数的后向时间模型无关控制算法, 并证明所提算法得到的时变LGF控制增益矩阵收敛于MTVRE的解; 另外, 证明所提算法不仅可以实现半全局一致性, 而且可以保证执行器饱和条件下的全局一致性控制, 并通过仿真实验进行论证.
本文的结构安排如下: 第1节首先介绍代数图论的相关知识, 并结合LGF方法介绍执行器饱和的离散时间MASs有限时域一致性控制问题的基于模型的求解方案. 第2节首先证明可以将执行器饱和的离散时间MASs有限时域一致性控制问题转化为执行器饱和的单智能体的最优控制问题, 接着提出基于TVPQF的后向时间迭代算法以逼近求解最优控制问题对应的MTVRE. 第3节提供仿真结果验证本文方法的有效性, 并进行对比实验, 比较性能指标突显本文方法的优越性. 第4节为结束语.
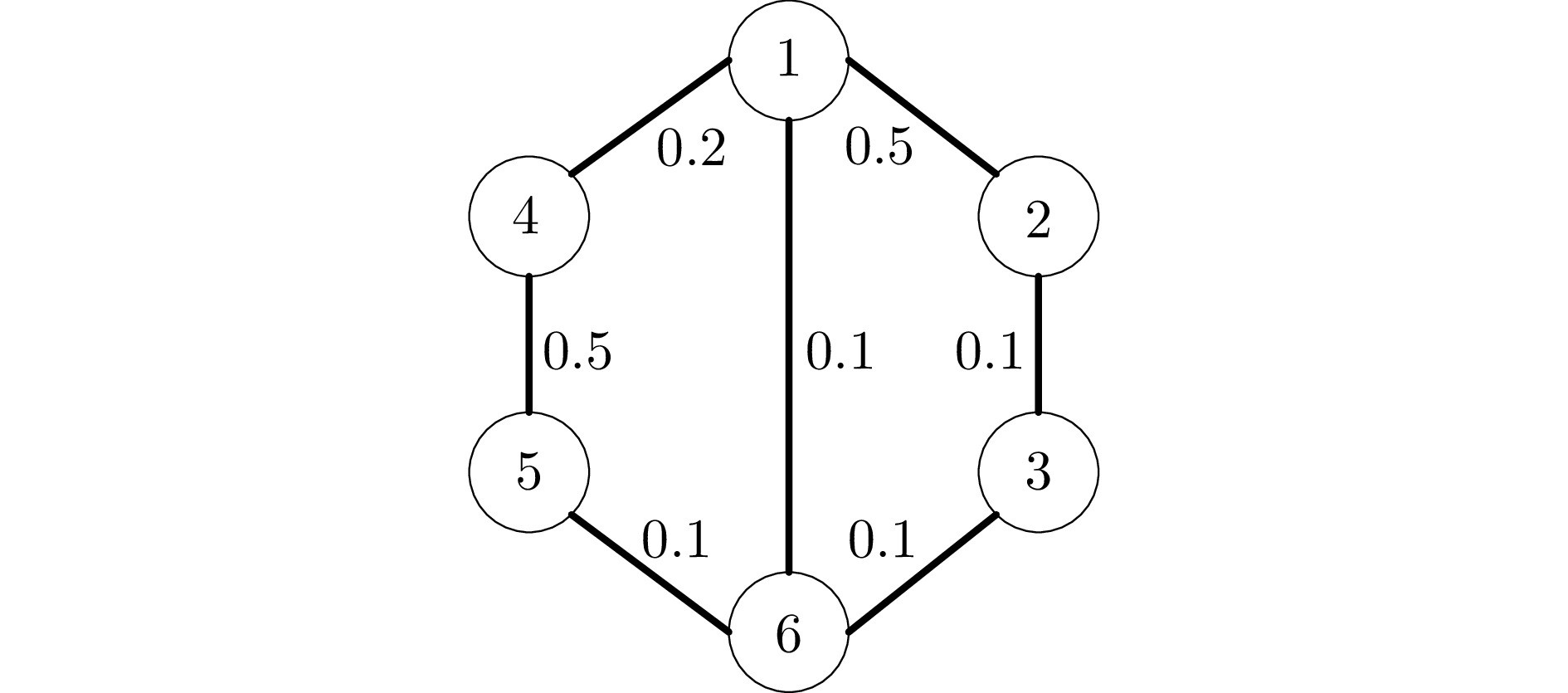
图 1 仿真1中MASs的通信拓扑
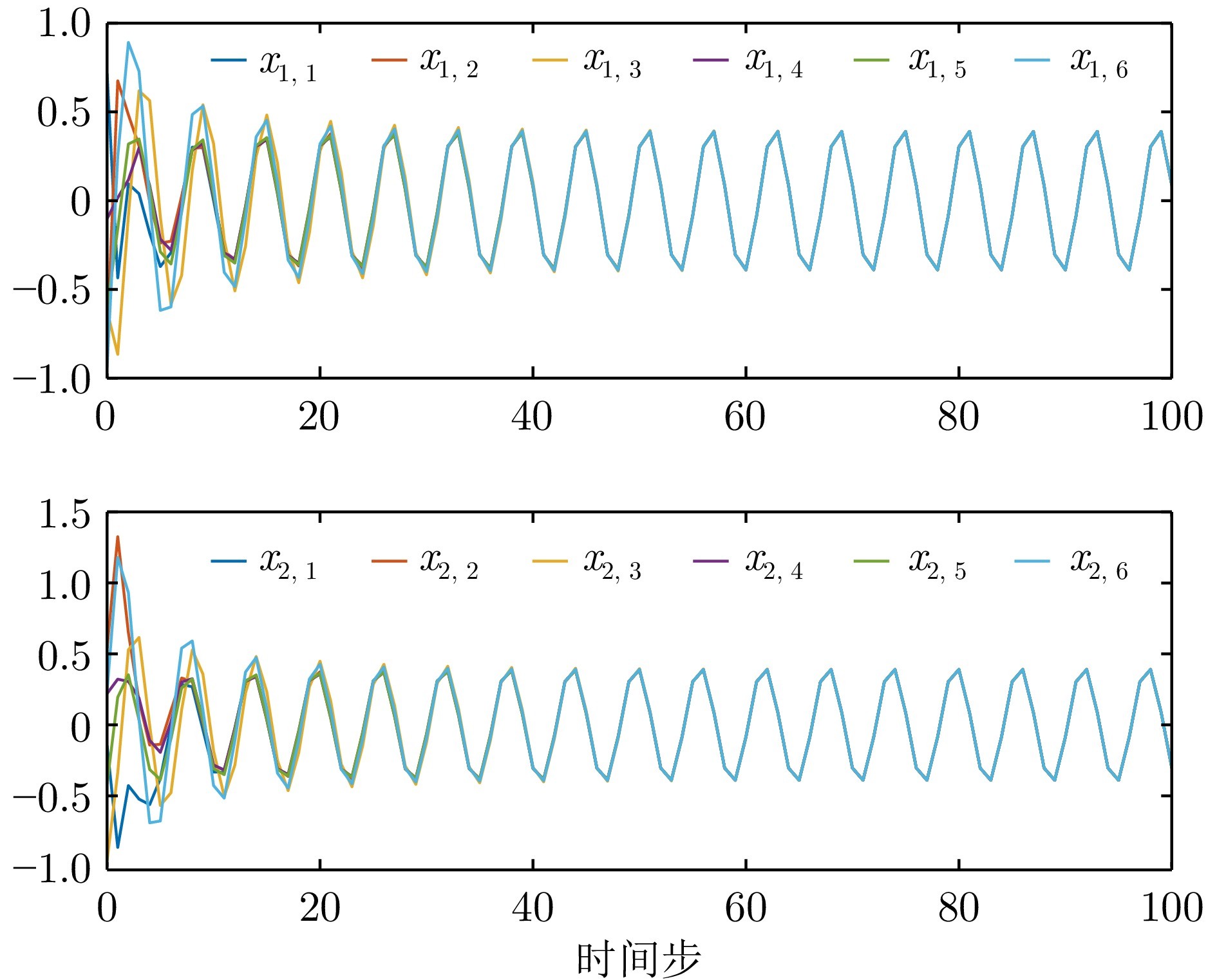
图 2 例1中智能体的状态
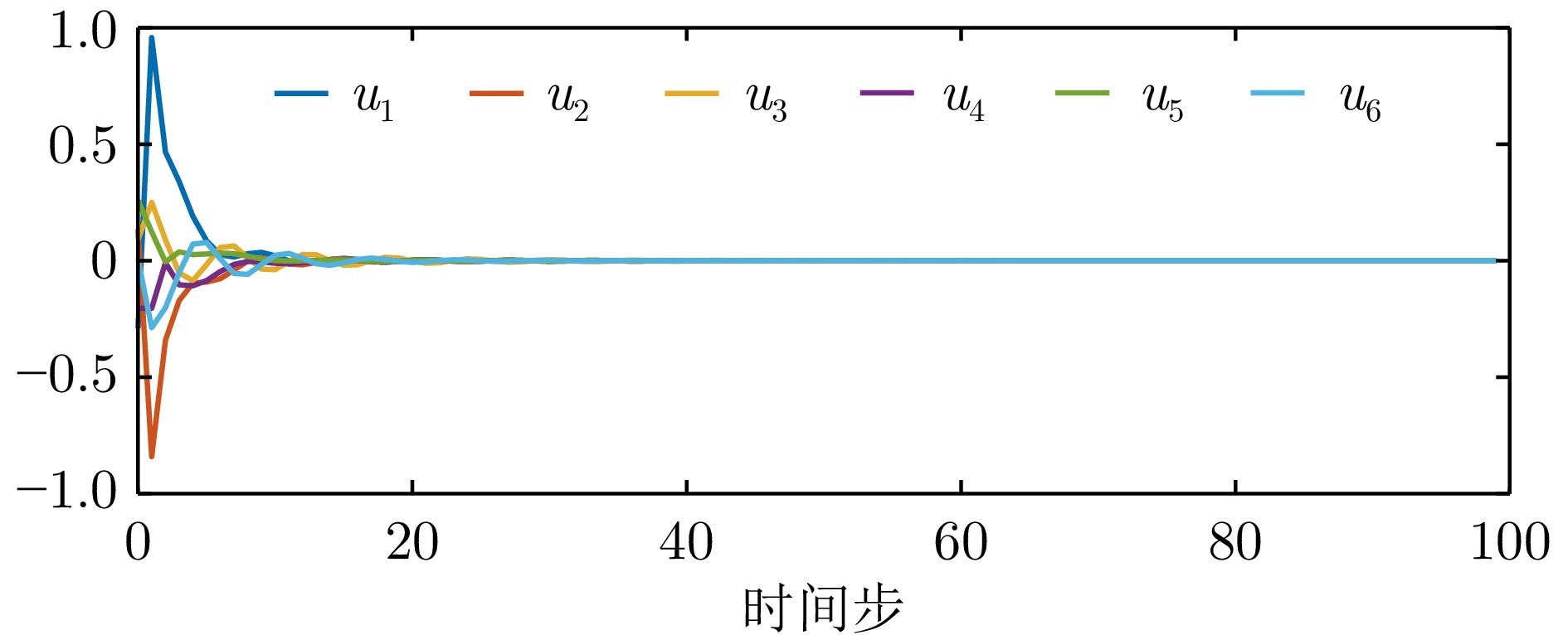
图 3 例1中智能体的控制输入
本文提出一种基于Q学习的数据驱动算法, 用于求解具有未知模型参数、执行器饱和的离散时间MASs的有限时域一致性控制问题. 首先结合LGF方法, 将执行器饱和的有限时域一致性控制问题转化为执行器饱和的单智能体最优控制问题, 给出原问题的控制器设计方案. 然后在未知系统模型参数的条件下, 设计基于Q学习的数据驱动后向时间算法逼近求解MTVRE, 用以获取LGF控制增益矩阵, 并给出该算法的收敛性说明. 最后, 给出仿真结果来验证基于Q学习的有限时域一致性控制算法的有效性, 并证明智能体的初始状态会影响收敛速度的问题. 同时, 还给出对比实验来评价有限时域一致性控制算法与无限时域一致性控制算法的控制效果.
在本文提出的方法中, 有限时域参数 $ \tau $ 作为算法1的输入参数, 其在参数选择过程中需凭借经验来进行设定. 在未来的研究中, 将探讨更为精确的有限时域参数设置方法, 以确定 $ \tau $ 的边界条件, 从而设定合理的有限时域参数 $ \tau $.
作者简介
王巍
中南财经政法大学副教授. 2019年获得中国地质大学(武汉)控制科学与工程专业博士学位. 主要研究方向为强化学习与自适应动态规划, 多智能体系统, 有限时域最优控制. E-mail: imagef@zuel.edu.cn
王珂
天津大学助理研究员. 2023年获得天津大学控制科学与工程专业博士学位. 主要研究方向为强化学习与自适应动态规划, 微分博弈与应用, 事件触发方法. E-mail: walker_wang@tju.edu.cn
黄自鑫
武汉工程大学副教授. 2020年获得中国地质大学(武汉)控制科学与工程专业博士学位. 主要研究方向为软体机器人, 强化学习. E-mail: huangzx@wit.edu.cn
王乐君
重庆邮电大学讲师. 2022年获得中国地质大学(武汉)控制科学与工程专业博士学位. 主要研究方向为机器人智能控制技术. E-mail: wanglj@cqupt.edu.cn
穆朝絮
天津大学教授. 2012年获得东南大学控制科学与工程专业博士学位. 主要研究方向为强化学习, 自适应学习系统, 无人优化与控制. 本文通信作者. E-mail: cxmu@tju.edu.cn
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1483394.html?mobile=1
收藏