博文
基于模糊神经网络在线自学习的多智能体一致性控制
|
引用本文
张宪霞, 唐胜杰, 俞寅生. 基于模糊神经网络在线自学习的多智能体一致性控制. 自动化学报, 2025, 51(3): 590−603 doi: 10.16383/j.aas.c240451
Zhang Xian-Xia, Tang Sheng-Jie, Yu Yin-Sheng. Multi-agent consensus control based on online self-learning fuzzy neural network. Acta Automatica Sinica, 2025, 51(3): 590−603 doi: 10.16383/j.aas.c240451
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240451
关键词
多智能体系统,自适应动态规划,动态模糊神经网络,分布式一致性控制,在线学习
摘要
针对多智能体系统分布式一致性控制问题, 提出一种新的融合动态模糊神经网络(Dynamic fuzzy neural network, DFNN)和自适应动态规划(Adaptive dynamic programming, ADP)算法的无模型自适应控制方法. 类似于强化学习中执行者−评论家结构, DFNN和神经网络(Neural network, NN)分别逼近控制策略和性能指标. 每个智能体的DFNN执行者从零规则开始, 通过在线学习, 与其局部邻域的智能体交互而生成和合并规则. 最终, 每个智能体都有一个独特的DFNN控制器, 具有不同的结构和参数, 实现了最优的分布式同步控制律. 仿真结果表明, 本文提出的在线算法在非线性多智能体系统分布式一致性控制中优于传统基于NN的ADP算法.
文章导读
多智能体系统的分布式一致性控制受到鸟群、蚁群等自然生物系统的启发, 近年来受到越来越多的关注[1−2]. 非线性多智能体系统的分布式领导–跟随一致性控制算法在许多新兴技术中发挥着关键作用, 包括生物系统和无人系统集群等[3−5]. 相比于集中式多智能体系统的最优一致性控制, 分布式多智能体系统的最优一致性控制凭借其更大的适应性和灵活性, 成为目前研究人员关注的焦点问题之一[6−16].
最优分布式一致性问题试图设计一种分布式算法, 既能同步所有智能体, 又能使通信有向图的能量成本最小[17−19]. 最优分布式一致性控制由一致性控制发展而来. 目前, 一致性控制已经取得许多显著的成果[20−22], 但值得注意的是, 这些成果都只关注多智能体系统的一致性, 在实际中, 不仅需要保证系统的一致性, 还需要构造一个能够满足一定性能指标的分布式控制器. 在多智能体系统中, 每个智能体都依赖于自身和相邻智能体的行为, 这类似于多人游戏的协调控制. 学者们开始利用博弈论研究多智能体系统的最优一致性控制[23]. 博弈论为研究多智能体一致性控制问题提供了一个理想的工具[24]. 博弈论研究智能体的行为如何相互作用. 系统中的每个智能体独立地优化自己的性能指标函数并做出最优决策, 最终使多智能体系统收敛到纳什均衡解. 由于多智能体系统中每个智能体的策略受到自身及其邻居行为的影响, 为了获得纳什均衡解, 必须求解高耦合哈密顿–雅可比–贝尔曼(Hamilton-Jacobi-Bellman, HJB)方程[25]. 由于HJB方程包含智能体的动态系统信息和偏微分项, 所以高耦合HJB方程的解析解很难得到, 甚至在智能体的动态系统模型未知的情况下, 不可能得到解析解[26].
为克服这一挑战, Werbos[27]提出自适应动态规划(Adaptive dynamic programming, ADP)来处理多智能体的分布式一致性问题[28−29]. ADP是一种由强化学习(Reinforcement learning, RL)和动态规划派生而来的解决最优控制问题的有效方法. 该方法力图获得近似最优控制律, 并克服传统动态规划方法所带来的“维数诅咒”难题. 随着ADP方法的发展, 近年来许多基于ADP的方法被应用于多智能体系统来处理分布式一致性问题[30−35]. 神经网络(Neural network, NN)对于非线性系统有着良好的拟合效果, 因此常常被用来解决非线性系统问题. Wang等[36]提出一种基于神经网络的鲁棒最优控制算法, 在指定成本函数的情况下实现最优性控制. Wei等[33]利用神经网络研究异构多智能体系统, 来解决异构多智能体系统的最优分布式同步控制. Zhang 等[37]提出一种数据驱动的一致性控制算法, 并使用两个神经网络分别逼近执行者网络和评论家网络来实现离散时间多智能体系统的最优一致性控制. 为加速基于ADP算法的收敛性, 很多研究集中在自适应评论家设计上[37], 如Cai等[38]提出一种广义模糊双曲模型(Generalized fuzzy hyperbolic model, GFHM)来近似值函数, Wang等[39]提出一种基于稀疏核机的自适应评论家设计. 综上所述, 大多数研究工作都集中在评论家网络的自适应逼近上, 相比之下, 对执行者网络的自适应逼近的研究却很少. 文献综述表明, 执行者网络通常采用传统的神经网络进行近似, 并且神经网络的结构是不变的[39−40]. 这样会产生疑难问题: 1)如何解释神经网络控制器? 2)如何确定神经网络的结构? 3)多智能体系统采用多个神经网络近似执行者, 在训练过程中很难保证多个神经网络的收敛性, 如何提高最终策略的质量?
有少量文献试图解决上述问题. 文献[41]提出一种模糊执行者–评论家强化学习网络, 其使用自适应径向基函数(Radial basis function, RBF)网络逼近执行者和评论家网络, 并将两者合并为一个网络. 文献[42]提出一种新的循环区间2型Takagi-Sugeno-Kang (TSK)模糊神经网络(RIT2TSK-FNN)控制器结构, 并通过列文伯格–马夸尔特(Levenberg-Marquardt, LM)方法更新执行者的参数. 文献[43]提出一种基于区间2型TSK模糊神经网络的执行者–评论家新结构. 然而, 上述文献中的方法仅适用于单个智能体.
基于上述讨论, 针对非线性多智能体系统, 本文提出一种新的基于动态模糊神经网络(Dynamic fuzzy neural network, DFNN)的ADP多智能体分布式最优一致性控制(DFNN-ADP)方法. 相较于传统的NN算法, DFNN的优势明显. 首先, DFNN能够处理不确定性和模糊性, 从而提高了网络对噪声和不确定数据的鲁棒性. 其次, 模糊神经网络结合模糊逻辑和神经网络的优点, 模糊规则和隶属度函数的使用可以提供更直观的决策依据, 增加了模型的可解释性. 此外, DFNN能够动态调整其模糊规则和参数, 从而适应不同的输入模式和环境变化, 使DFNN在处理复杂变化的实际问题时表现更出色.
不同于传统基于NN的ADP (NN-ADP)方法和集中式一致性控制方法, 本文针对非线性多智能体系统, 采用基于DFNN的自适应动态规划方法实现最优分布式一致性控制. 所提出的DFNN-ADP方法, 在系统模型完全未知的情况下, 仅利用系统的实时输入输出数据, 解决了离散时间非线性领导–跟随多智能体系统的最优分布式一致性问题. 该方法利用DFNN和NN分别逼近控制策略和性能指标. 随着在线学习算法的运行, 每个智能体都有一个独特的DFNN控制器, 具有不同的结构和参数, 实现了最优的分布式同步控制律.
本文的主要贡献如下:
1)提出一种融合DFNN和ADP算法的多智能体分布式无模型自适应控制方法;
2)首次提出具有结构自组织和参数自学习的动态模糊神经网络的多智能体控制方法;
3)相较于传统基于NN的ADP算法[39], 本文所提算法表现出更好的抗干扰能力和更快的收敛速度.
本文的结构安排如下: 第 1 节介绍一些初步的知识, 如图论、最优一致性控制的证明和纳什均衡; 第 2 节介绍基于策略迭代的ADP方法; 第 3 节提出一种新的基于DFNN的ADP方法, 用于非线性多智能体系统的分布式一致性控制; 第 4 节给出仿真实验, 以证明所提出方法的有效性; 第5节为结束语.
图 1 基于DFNN-ADP的多智能体一致性控制结构
图 2 DFNN结构
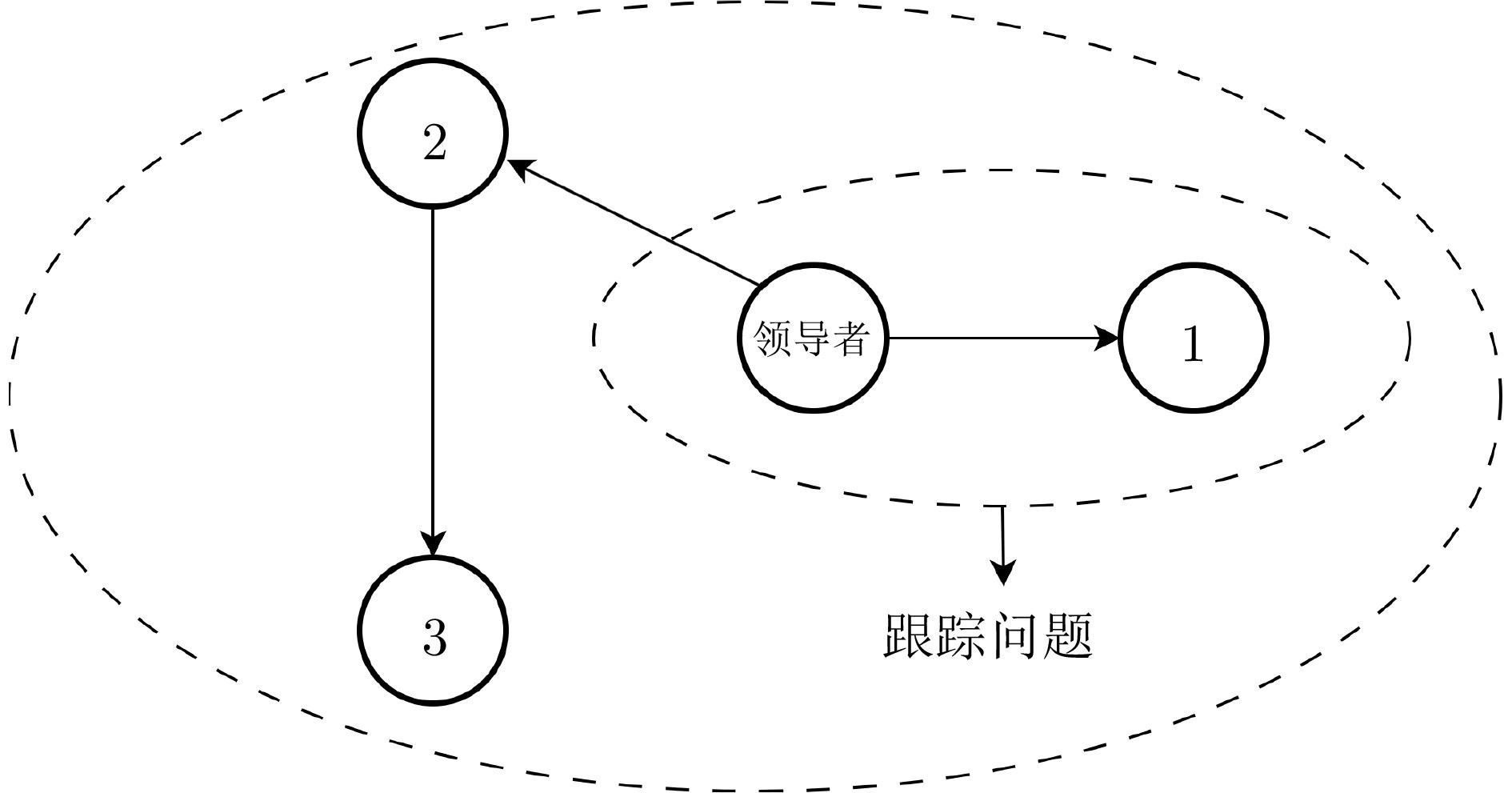
图 3 多智能体系统的标准一致性问题
本文针对离散一阶非线性多智能体系统的一致性问题提出一种基于策略迭代的自适应动态规划算法, 该算法在不知道多智能体具体数学模型的情况下, 通过策略迭代的方法求解HJB方程, 使得整个多智能体系统不仅状态达成一致而且整体能量消耗最小. 根据多智能体的性能指标函数提出HJB方程, 并通过策略迭代的方式求解HJB方程, 同时证明该方法的收敛性和稳定性. 在使用执行者–评论家网络结构对控制策略和性能指标进行逼近时, 采用动态模糊神经网络代替传统神经网络对执行网络进行逼近, 该网络具有自学习自组织的特点, 避免了多项式神经网络激活函数构造困难、神经元个数和层数难以确定的问题. 通过仿真实验, 将该方法与基于多项式激活函数的神经网络的ADP算法进行对比, 充分验证了该算法具有更优秀的收敛能力和适用性.
本文所提出算法的实验是针对仿真环境来进行的, 算法应用到实际中时, 往往会有各种意想不到的问题, 在后续的研究中, 考虑将算法应用到多无人艇的最优一致性控制中. 另外, 在处理最优问题上, 本文仅从仿真实验中证实了DFNN是优于传统NN的, 在理论上尚不能证明. 在未来的研究中, 如何从理论上证明DFNN优于传统NN, 将是一个重要的研究工作.
作者简介
张宪霞
上海大学机电工程与自动化学院教授. 2008年获得上海交通大学控制理论与控制工程专业博士学位. 主要研究方向为群体智能, 多智能体无模型智能控制, 复杂系统的智能控制与建模, 机器人视觉伺服. 本文通信作者. E-mail: xianxia_zh@t.shu.edu.cn
唐胜杰
上海大学机电工程与自动化学院硕士研究生. 2023年获得江苏科技大学自动化专业学士学位. 主要研究方向为多智能体协同控制. E-mail: tang_sheng_jie@shu.edu.cn
俞寅生
上海大学机电工程与自动化学院硕士研究生. 2023年获得上海大学模式识别与智能系统专业硕士学位. 主要研究方向为强化学习和多智能体协同控制. E-mail: 1185121733yss@gmail.com
https://wap.sciencenet.cn/blog-3291369-1483068.html
上一篇:【目录】IEEE/CAA JAS第12卷第3期
下一篇:异构非线性多智能体系统无模型输出一致性控制