博文
面向RTK定位的整数约束型渐进高斯滤波方法
|
引用本文
杨旭升, 李唯诣, 张文安. 面向RTK定位的整数约束型渐进高斯滤波方法. 自动化学报, 2025, 51(2): 366−375 doi: 10.16383/j.aas.c240384
Yang Xu-Sheng, Li Wei-Yi, Zhang Wen-An. Integer-constrained progressive Gaussian filtering method for RTK positioning. Acta Automatica Sinica, 2025, 51(2): 366−375 doi: 10.16383/j.aas.c240384
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240384
关键词
渐进高斯滤波,RTK 定位,模糊度固定,整数约束
摘要
本文研究了卫星信号干扰下 RTK (Real-time kinematic)整周模糊度固定问题, 提出一种基于整数约束型渐进高斯滤波的 RTK 定位方法. 首先, 结合贝叶斯推理与同伦方法优势, 导出一种兼容整数、浮点状态的渐进高斯滤波框架. 其次, 构造从先验分布到后验分布的同伦路径, 以目标浮点状态与模糊度固定的迭代求解来提高信号干扰情形下的整周模糊度固定率. 特别地, 通过渐进地融合卫星双差信息来降低线性化误差, 进而提升对目标状态后验分布的逼近精度. 最后, 通过车载 RTK 实验及后处理分析, 验证了所提方法的有效性和优越性.
文章导读
作为一种 GNSS (Global navigation satellite system)高精度定位技术, RTK (Real-time kinematic)定位在测绘、农业和无人驾驶等领域具有巨大的发展潜力[1−3]. 通过差分处理来自基站和流动站的伪距和载波相位观测数据, RTK 技术能够有效地降低大气延迟误差、钟差等卫星系统误差, 从而提高定位精度[4−5]. 载波相位观测的整周模糊度固定是实现 GNSS 高精度定位的重要前提和基础. 然而, 由于多径效应、信号遮挡以及卫星几何分布等因素对观测质量和冗余性具有影响[6−7], 这将增加模糊度固定的难度同时降低定位准确度.
针对 GNSS 模糊度固定问题, 以最小二乘模糊度降相关平差 (Least-square ambiguity decorrelation adjustment, LAMBDA)算法应用最为广泛[8]. 在模糊度残差平方和最小准则下, 该算法利用整数高斯变换将模糊度协方差矩阵进行去相关, 同时利用对角元素排序以构造更优的搜索空间, 这样极大地降低了模糊度搜索时间. 在此基础上, 文献[9] 通过引入选主元法、贪心算法等, 进一步提高了计算速度和去相关效能. 值得注意的是, 最小二乘法对动态变化适应性差且对噪声和异常值等较为敏感. 为此, 文献[10] 等提出利用卡尔曼滤波 (Kalman filter, KF)等方法解算双差量测以获取模糊度浮点解, 通过 LAMBDA 算法还原载波相位的整周特性, 从而得到整周模糊度固定解. 然而, 考虑 LAMBDA 算法对初值选取较为敏感, 同时, 受城市峡谷、高架桥等复杂环境影响, 信号遮挡和多径效应等因素使得卫星信号强度分布不均匀, 进而引起测量噪声增大. 若未能及时补偿该量测不确定性, 将严重影响滤波精度和稳定性[11], 使得模糊度浮点解难以收敛到模糊度固定解[12].
另一方面, 对于 RTK 定位中模糊度浮点解的求解问题, 已有一系列非线性滤波方法被相继提出[13−15]. 扩展卡尔曼滤波器 (Extended Kalman filter, EKF)凭借其较高的计算效率与实现的简便性, 已成为 GNSS 定位领域内广泛应用的滤波技术之一[16]. 然而, 受非视距等因素的影响, 复杂环境下 GNSS 信号的衰减问题将导致量测不确定性增加; 此外, 根据泰勒级数展开原理, 不难发现, 由忽略高阶项引起的截断误差将间接地随量测不确定性增大而增大. 为克服上述问题, 文献[17] 采用矢量跟踪环路 (Vector-tracking loop, VTL)模型, 结合迭代扩展卡尔曼滤波 (Iterative extended Kalman filter, IEKF), 提高了滤波性能. 文献[18−19] 基于变分贝叶斯推理方法, 提出具有检测异常值功能的鲁棒扩展卡尔曼滤波 (Robust extended Kalman filter, REKF), 该方法虽有效提高了在多径效应影响下的滤波性能, 但同时也损失了整体的模糊度固定率. 文献[20] 基于载波噪声密度比和标准化残差对不同卫星量测进行重加权, 设计一种鲁棒滤波方法, 有效地减弱了多径效应和量测粗差对定位系统带来的影响. 不同于上述鲁棒方法, 文献[21] 基于贝叶斯框架提出一种渐进高斯滤波方法, 通过逐步地提取量测信息来补偿量测不确定性, 在一定程度上解决了量测信息缺失造成的估计误差增大问题. 文献[22−23] 进一步提出一种自适应渐进高斯滤波方法, 通过收敛性分析给出渐进量测更新的截止条件, 有效避免了过估计问题. 在此基础上, 针对量测信息中包含的复杂噪声, 文献[24] 分别从空间、时间维度对量测进行相容性分析与分类处理并引入渐进量测更新与引导机制, 隐式地补偿量测不确定性. 然而, 上述方法虽然都在一定程度上提高了滤波器的鲁棒性, 但 RTK 定位系统中浮点状态估计和模糊度固定具有较强的耦合性, 使得当前滤波方法难以适用兼容整数、浮点状态的估计问题.
针对以上问题, 本文提出一种面向 RTK 定位的整数约束型渐进高斯滤波方法. 首先, 基于贝叶斯推理导出整数约束下的渐进高斯滤波框架. 其次, 通过引入伪时间常数, 渐进地融合双差量测信息, 以减少线性化误差带来的不良影响. 特别地, 利用渐进量测更新和模糊度固定的迭代执行, 来提高在信号干扰下的模糊度固定率. 最后, 通过车载实验采集实时卫星数据并进行后处理分析, 验证了所提算法的有效性和优越性.
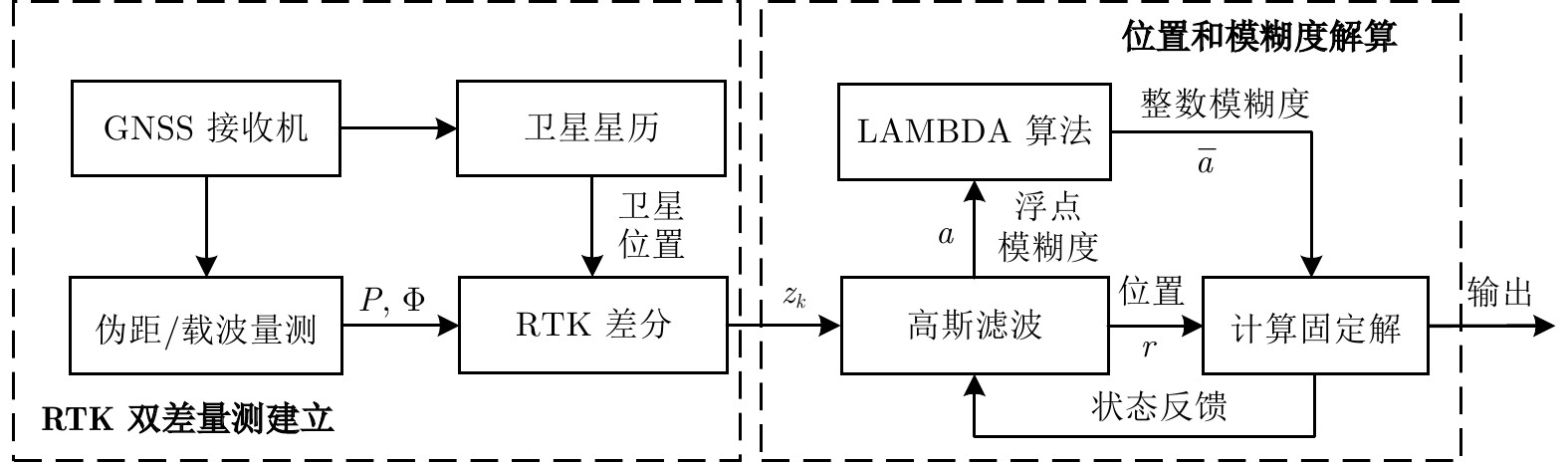
图 1 基于高斯滤波的 RTK 定位框图
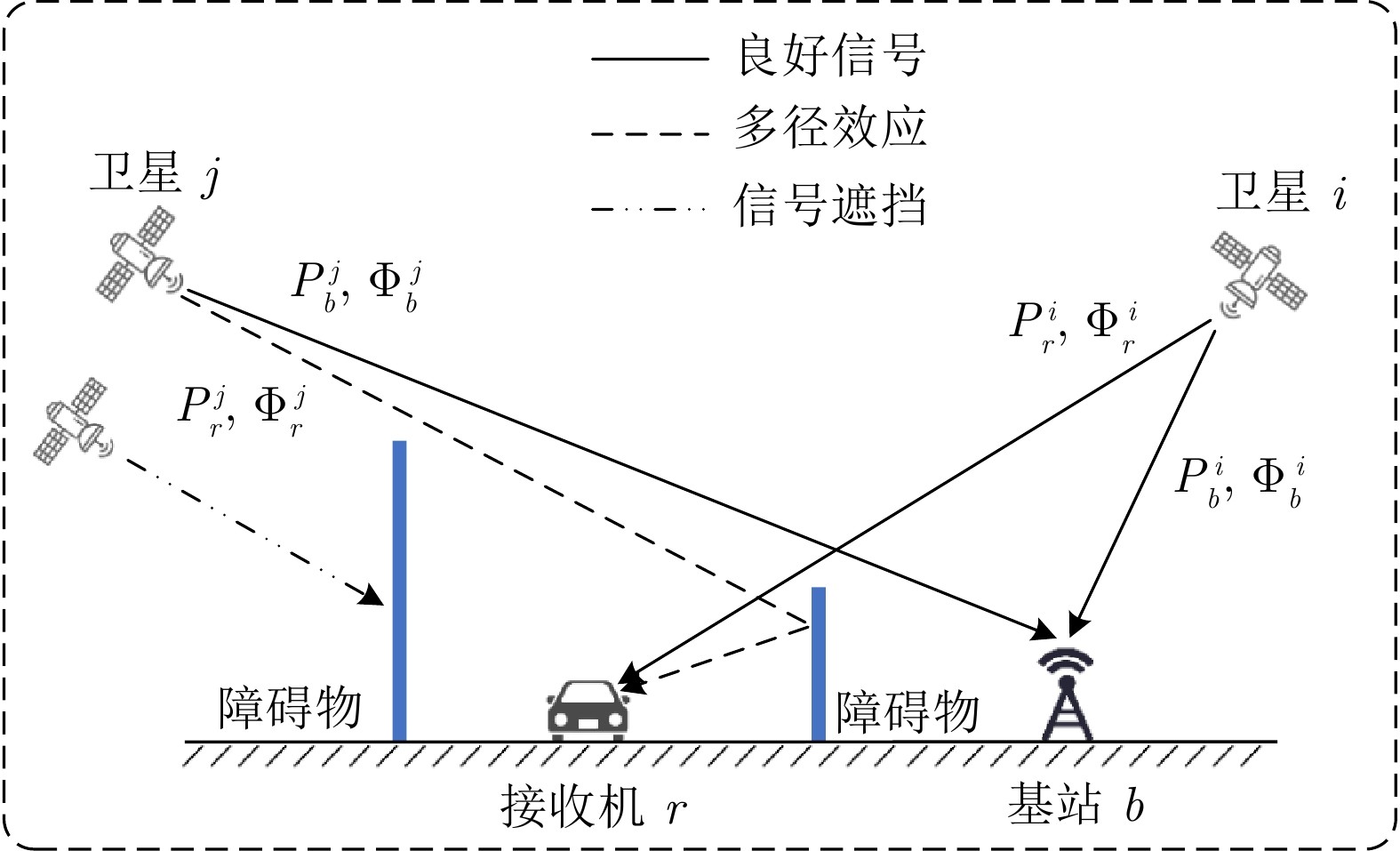
图 2 RTK 定位示意图
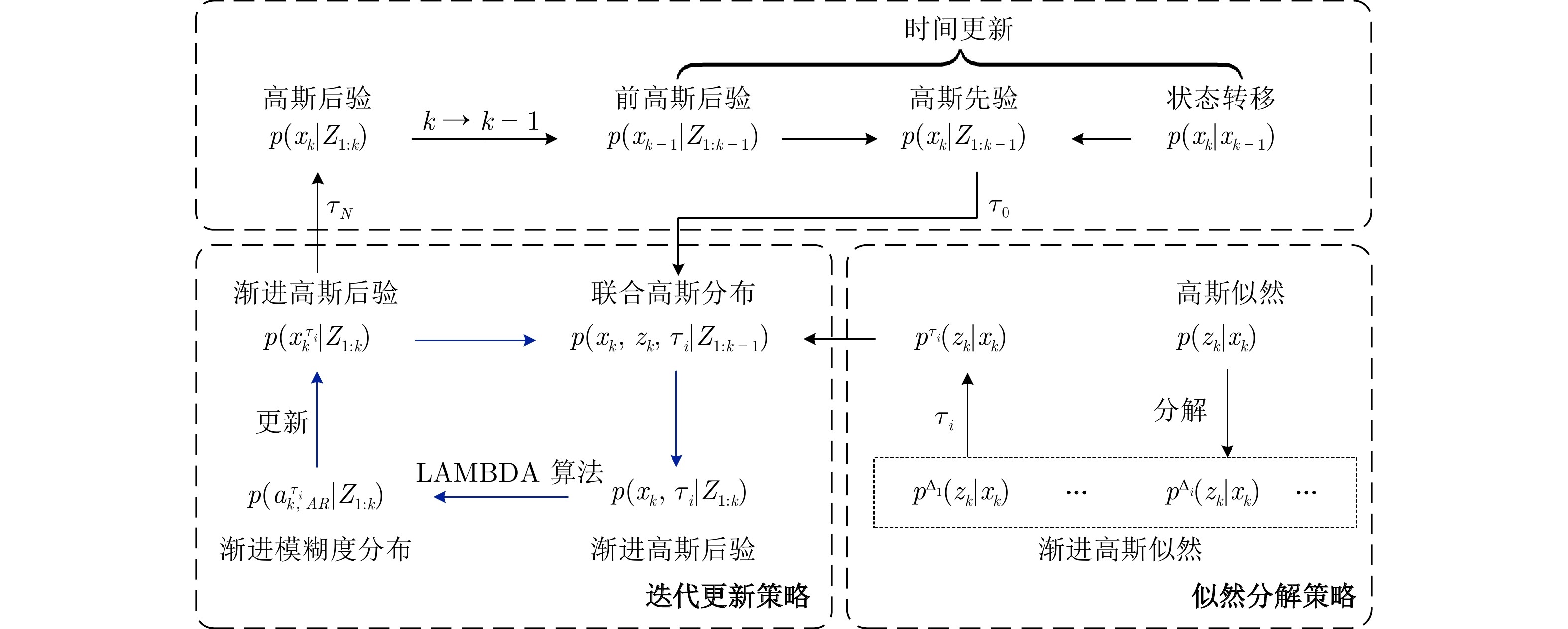
图 3 整数约束型渐进高斯滤波框架
针对 GNSS 信号干扰情况下的模糊度固定率下降问题, 提出一种面向 RTK 定位的整数约束型渐进高斯滤波方法. 该方法通过引入渐进高斯滤波, 迭代地执行渐进量测更新和模糊度固定. 这样, 利用渐进后验估计引导模糊度固定, 提高了定位结果的精度和鲁棒性. 实验结果表明, 相较于其他方法, 本文所提算法能够有效提高定位系统的固定率以及估计精度, 且在卫星失锁的情况下具有良好的收敛速度. 当然, 本文在卫星数据预处理和模型约束方面尚未深入展开. 在未来的研究中, 将考虑采用更优的选星策略, 并引入更多的约束方法, 对不同遮挡程度的卫星进行差异化处理, 进一步提升方法的自适应性, 并探索更具动态适应性的滤波策略.
作者简介
杨旭升
浙江工业大学信息工程学院副教授. 主要研究方向为多源信息融合估计和目标定位. E-mail: xsyang@zjut.edu.cn
李唯诣
浙江工业大学信息工程学院硕士研究生. 主要研究方向为RTK定位和信息融合估计. E-mail: lwy_2210@163.com
张文安
浙江工业大学信息工程学院教授. 主要研究方向为多源信息融合估计和网络化系统. 本文通信作者. E-mail: wazhang@zjut.edu.cn
https://wap.sciencenet.cn/blog-3291369-1479381.html
上一篇:好文推荐│不确定性感知深度学习:实现可靠故障诊断的有力工具
下一篇:基于颜色转移和自适应增益控制的混合水下图像增强