124. 数学上有趣的黎曼 zeta 函数零点解是否都具有 a + ib 的形式?

Do mathematically interesting zero-value solutions of the Riemann zeta function all have the form a + ib?

题记：无需深究细节。自 19 世纪中叶以来“黎曼猜想”一直是数学池塘中的那条巨型的怪物鲶鱼。如果它真的存在，它将为数学家提供关于质数分布及其他长期未解之谜的丰富信息。

1 引言

这个科学问题就是鼎鼎大名的黎曼猜想(Riemann conjecture)，介绍黎曼猜想和试图证明黎曼猜想的文章浩如烟海，所以本文只是关于这个猜想的科普介绍，主要的目的是能让那些对此好奇的人站在数学的汪洋大海面前能够一睹它的轮廓。同样，美国克雷数学研究所网站对该问题有一个简单的介绍：素数定理(prime number theorem, PNT)描述了素数(simple number，也翻译为质数)在自然数中的平均分布规律，而黎曼猜想则揭示了素数分布相对于该平均规律的偏差细节。该猜想由德国数学家波恩哈德·黎曼(Bernhard Riemann,1826–1866)在其 1859 年的论文中首次提出，论文的核心观点是：黎曼zeta函数ζ(s)的所有“非平凡零点”(non-trivial zeros)都是实部为1/2的复数，即这些非平凡的零点都位于复平面上一条实部为 Re(s) = 1/2 的临界线(critical line)上。1859 年黎曼提出猜想的那篇论文的题目就是：The number of prime numbers not greater than x(论不大于x的素数的个数)，而这个不超过实数 x 的素数的个数通常用函数 π(x) 来表示。人类关于素数的研究已经非常古老，在黎曼的研究工作之前，就有一个所谓的素数猜想，现在已经成为素数定理，它是由高斯和勒让德提出并最早由雅克·阿达马(Jacques Hadamard)与查尔斯·让·德拉·瓦莱布桑(Charles Jean de la Vallée Poussin)在1896年独立证明，他们的证明都是利用了复变函数论与黎曼 ζ(s) 函数的性质。素数定理的主要结论是当 x 很大的时候，即 x → ∞ 时，π(x) ∼ x/ln x 或者π(x) ∼ Li(x), 也可以简洁地写为：

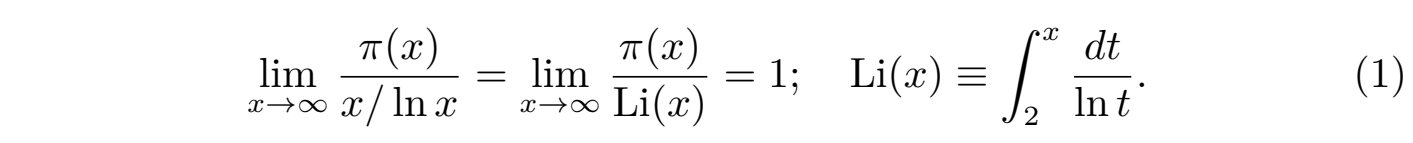
然而让人吃惊的是，1949年阿特勒·塞尔伯格(Atle Selberg)与保罗·爱多士(Paul Erdős)利用初等数论工具，仅仅借助组合数学和渐进分析就重新证明了素数定理，该证明虽然非常复杂但却颠覆了素数定理的证明必须依赖复分析的传统认知，体现了初等方法的基础性和深刻性。

由于素数是不能被分解为两个更小自然数乘积的数，所以素数作为数的基石无论在纯数学还是应用领域，都扮演着重要的角色。然而素数在自然数中的分布却显得非常随机和复杂，它们似乎并不遵循任何明显的分布规律。德国数学家黎曼在前人研究的基础上经过仔细分析发现：素数的分布规律与一个复杂函数的行为紧密相关，这个函数就是上面提到的黎曼ζ函数(Riemann Zetafunction)，其定义为：

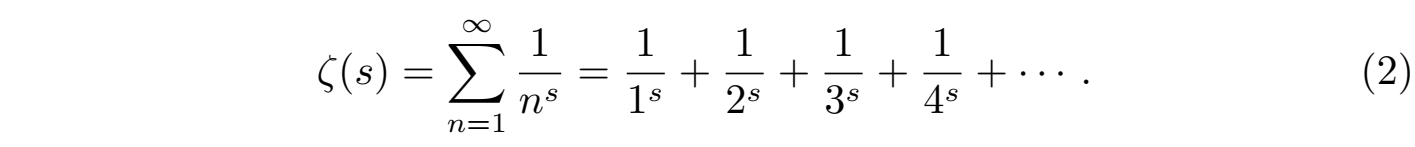
这个复变函数的零点可以用来估算素数的分布规律，并最终导致了黎曼猜想。黎曼猜想的核心论断是：方程 ζ(s) = 0 的所有非平凡零点 (non-trivial zeros)都位于复平面上的一条特定垂直线即实部 Re (s) =1/2的临界线上。截至目前，这一性质已经通过计算机验证了前10万亿(10¹³)个非平凡零点，这些解都毫不例外地满足黎曼猜想的断言。然而若能严格证明该猜想对所有非平凡零点均成立，那将有望解决围绕质数分布的诸多未解之谜，例如质数间隔的随机性、素数定理的精确误差估计，即可以把素数定理所给出结果的误差优化到：

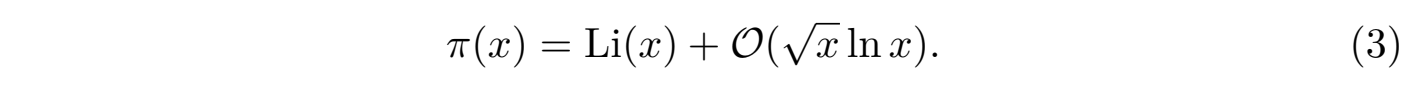
总之，目前已经有超过一千条数学命题都以黎曼猜想的成立为前提。

2 黎曼函数及其性质

下面我们来仔细介绍一下黎曼zeta函数ζ (s)。首先考虑如上式(2)无穷级数所定义的函数：

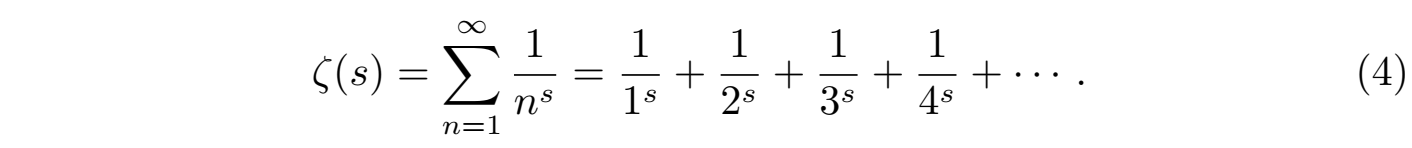
该函数的性质由自变量 s 的定义域决定。欧拉(Euler)最先研究了s 为正整数(s = 2, 3, 4, · · · )的情况，并给出了一个著名的求和公式：

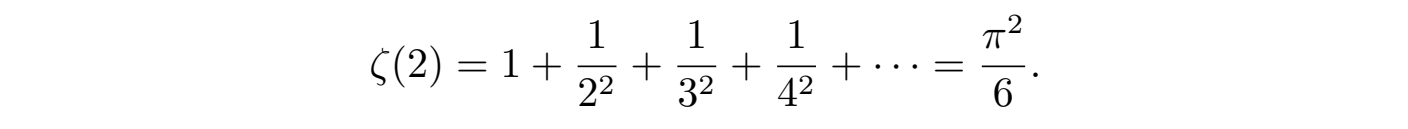
然而当s = 1时，这个无穷级数

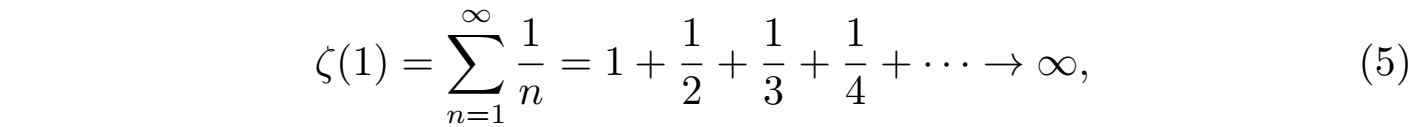
是发散的，称为调和级数，所以函数 ζ (1) 没有定义，需要从定义域中排除。这样我们就可以得到：当 s 是除1的自然数时，函数 ζ (s) 都能够被无穷级数 (4) 明确定义，并能够给出一些已知的求和结果：

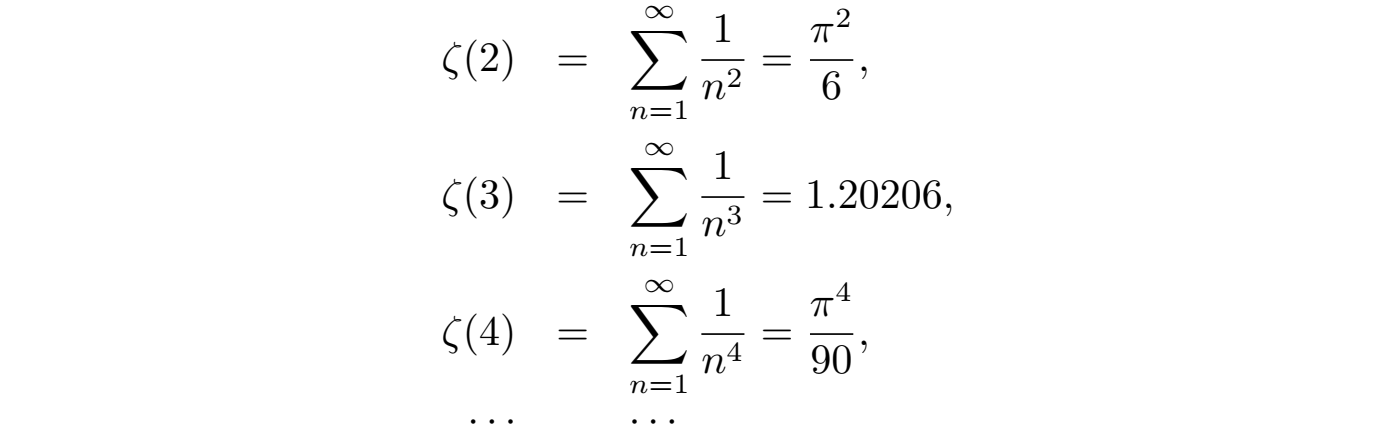
对于任何正偶数 (s = 2n, n ∈ N)，函数的求和结果存在如下的简单公式：

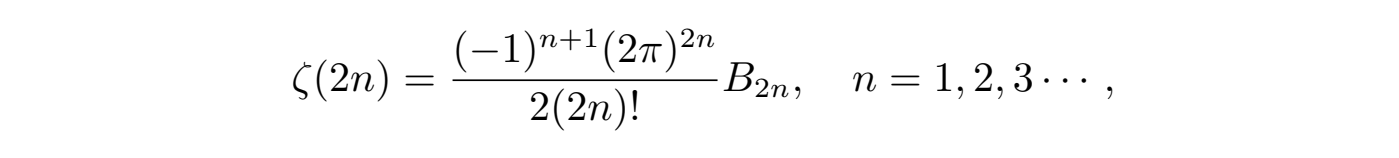
其中 B_2n 是伯努利数(Bernoulli numbers)，它是一个满足特定递归关系的有理数序列；而当 s 为奇数 2n+1 时，函数则没有简单的表达式 (关系很复杂)，此处从略。另一方面，当 s 取负整数时有：

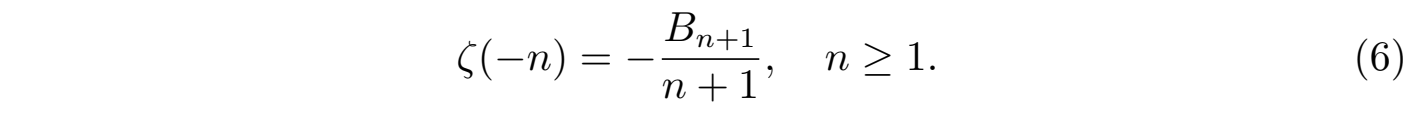
根据伯努力数B_m 的性质，所有奇数的伯努力数都为零，即当m是不为 1 的奇数时B_m = 0，即B₃ = B₅ = B₇ = · · · = 0，那么由式 (6) 可以得到：

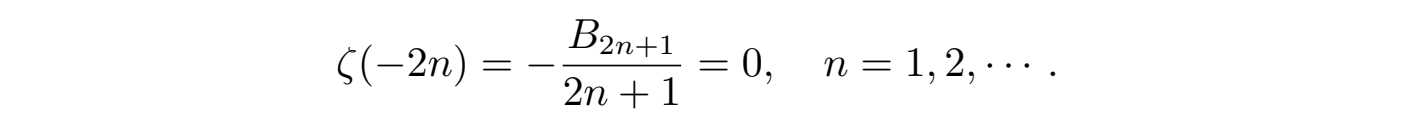
显然当s为负偶数s = -2n, n = 1, 2, 3, ...时函数 ζ (s) = 0，所以 -2, -4, -6, · · · 这些负偶数就称为ζ(s) 函数的平凡零点(trivial zeroes)。

此后，切比雪夫(Chebyshev)将 s 推广到实数域，在 {s | s > 1, s ∈ R} 上定义了 ζ 函数。显然当 s ≤ 1 时该函数无定义，比如：

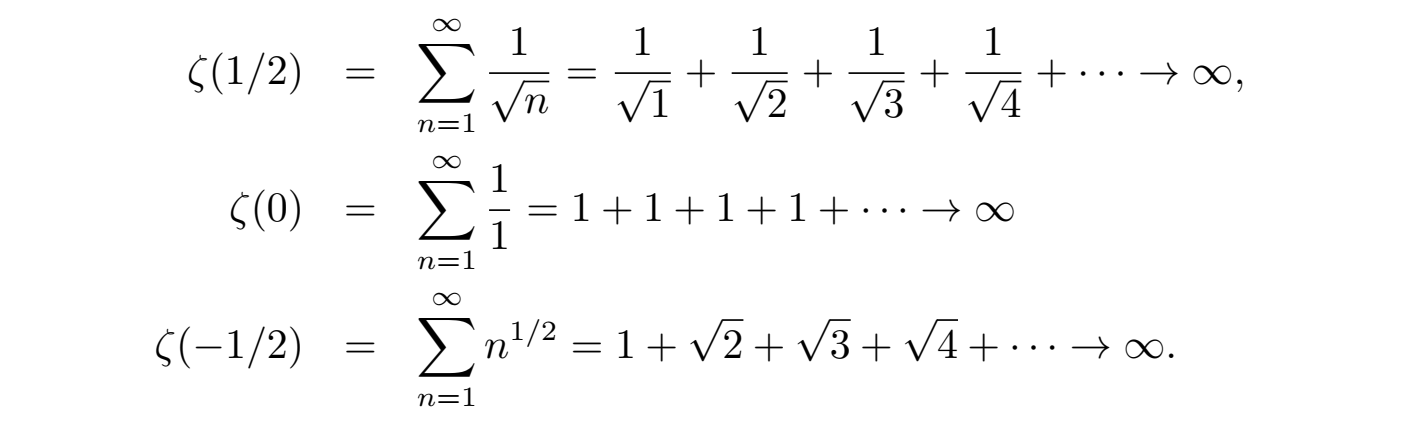
虽然在 s ≤ 1 这个区域函数都是无穷大，但它们之间有这样的关系 ζ(1) < ζ(1/2) < ζ(0) < ζ(−1/2) < ···，也就是函数在 s ≤ 1 这个发散区间随 s 的减小函数值(发散程度)是递增的。显然在这个无法定义函数值的区域 s ≤ 1，ζ函数的性质无法在实数的范围内获得有效地研究。

为了更好地利用 zeta 函数来研究素数的分布问题，黎曼将 zeta 函数推广到了复数域 s = σ + it，此时称为黎曼ζ 函数(Riemann zeta-function)。在这种情况下，复数域上的 zeta 函数 ζ(s) 在复平面上实部 Re(s) > 1 的区域上是解析函数(全纯函数)，这就意味着上述级数 (4) 在满足 σ > 1 时会绝对收敛于一个解析函数：

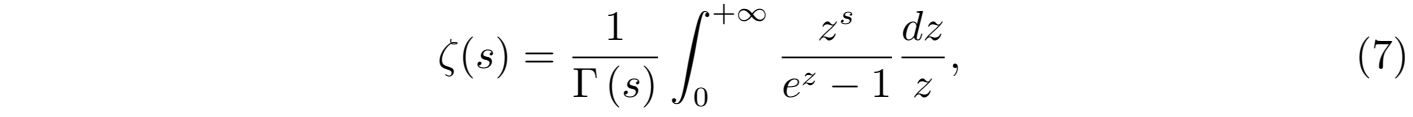
其中 Γ(s) 为著名的伽玛函数(gamma function)，积分 (7) 在 Re(s) > 1 的右半复平面成立。而对于其他区域黎曼利用伽玛函数的补充公式 Γ(1 − s)，依靠围道积分将ζ函数解析延拓到了整个复平面：

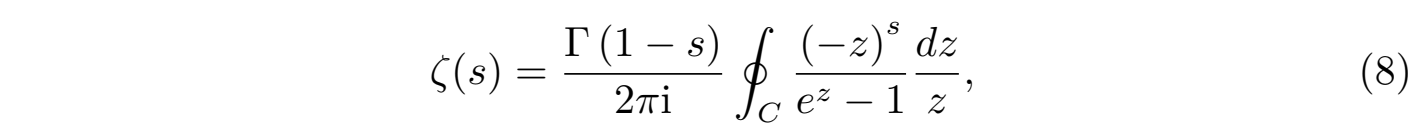
其中围道 C 环绕正实轴。但延拓积分 (8) 在 s = 1 处，级数 ζ(1) 做为调和级数 (5) 依然发散，但可以证明此时黎曼函数 ζ (x) 在整个复平面上是一个亚纯函数，只存在 s = 1 处唯一一个一阶极点，极点的留数为1：Res(s=1) = 1，并且满足如下的渐进关系：

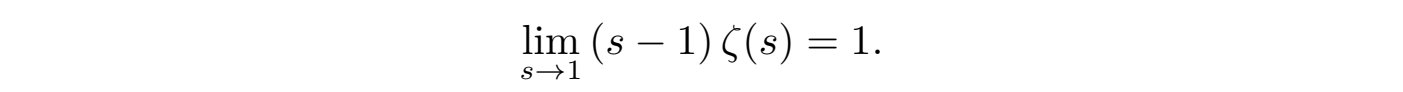
对于 (8) 所定义的黎曼 zeta 函数 ζ (s)，可以证明它满足如下的函数方程：

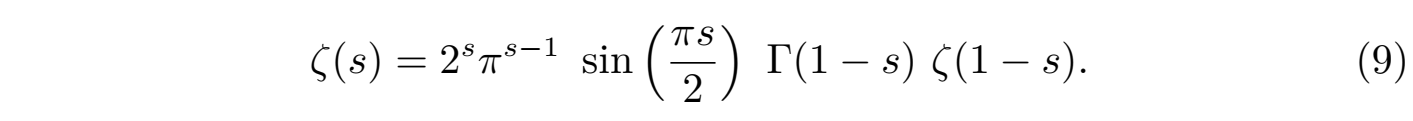
显然利用伽玛函数 Γ(s) 的补充公式及其如下性质：

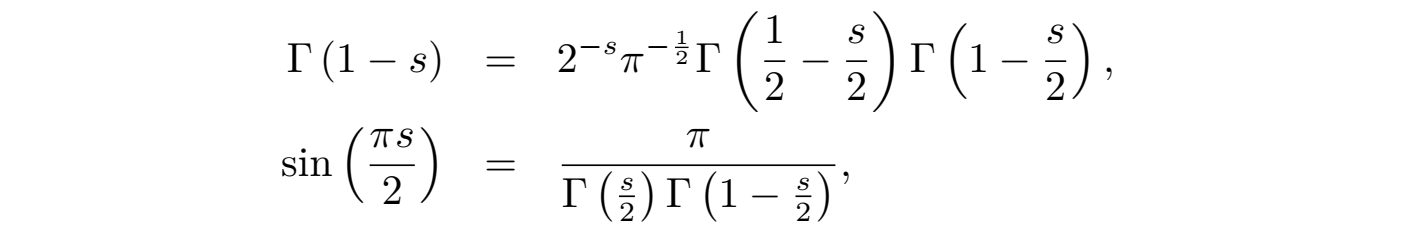
函数方程 (9)可以写为以下更为对称的形式：

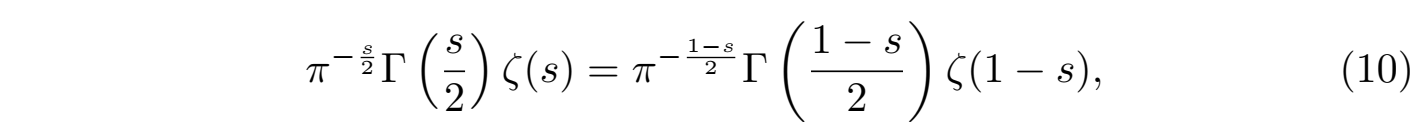
如果我们引入扩展的 zeta 函数(黎曼 ξ 函数)：

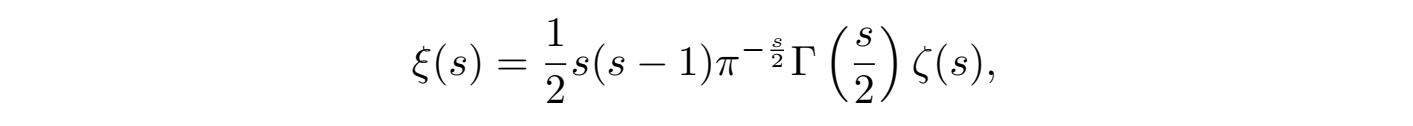
函数方程 (10) 就变成如下更加简洁的对称形式：

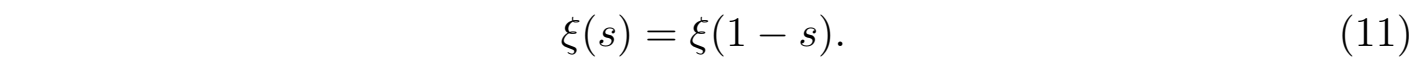
公式(11)中新引入的 ξ (s) 函数是在整个复平面上解析(无奇点)的全局整函数(entire function)，ξ(s)函数通过引入因子s(1−s)抵消了黎曼函数ζ(s) 在 s = 1 处的极点和伽玛函数 Γ(s/2) 在 s = 0 处的极点，从而函数方程 (11) 的对称性决定了函数 ξ(s) 在复平面是全局解析的整函数。显然 ξ(s) 函数的零点与 ζ(s) 函数的非平凡零点s₀一一对应并完全一致：ξ (s₀) ⇋ ζ (s₀)，而且它们的零点均位于临界带 0 < Re(s) < 1 内。而且 ξ(s) 函数的所有零点根据对称性 (11) 式是关于轴Re(s) =1/2镜像对称分布的。所以如果假定ξ (s₀) = 0 的零点s₀均为实数(s₀∈ R，即零点虚部为零)，那也就是说假如零点s₀都在实轴上，那么根据对称性s₀和 1 − s₀都是实轴上的零点。然而已经知道黎曼函数ζ (s)实数轴上除了负偶数(平凡零点)外，不存在其他零点 (即所谓的西格尔零点已被证明不存在)，因此，唯一满足对称性且都是位于实轴上的零点，那只能是 s₀ = 1 − s₀，不然s₀和1 − s₀就是实轴上两个不同的零点，所以只能得到 s₀ =1/2 ，这样就得到ξ (s₀)的零点的实部必须为 1/2。由此可见利用ξ(s)函数黎曼猜想(所有ξ(s)函数非平凡零点实部为1/2)可等价表述为：ξ(s)函数的所有零点均为实数。

3 黎曼函数与素数的关系

我们讨论黎曼函数ζ(s)的零点是因为该函数的零点可以给出关于素数的分布规律，那ζ(s)函数和素数之间到底存在怎样的关系？让我们先回到当初s为实数的情况，我们会发现当级数(4)收敛时有以下等式成立：

如果我们使用几何级数的公式：

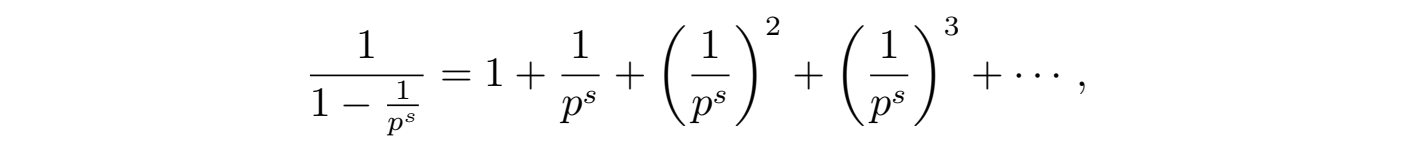
并考虑任何大于 1 整数 n 的算术基本定理，即整数的唯一素数分解定理：

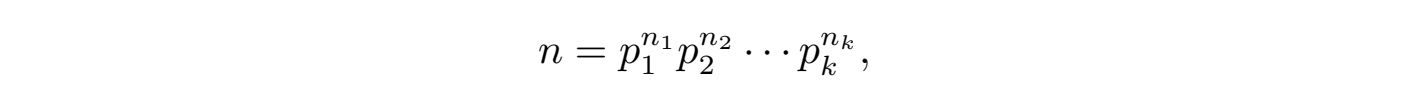
其中 p₁ < p₂ < ··· < p_k 是素数，n₁, n₂, ···, n_k 是正整数，并将它们带入式(12)右边的乘积之中，展开后重新进行排列，我们会发现 zeta 函数ζ(s) 的无穷求和形式和乘积形式 (12) 完全等价。函数 ζ(s) 的级数求和等于无穷乘积的证明首先由莱昂哈德·欧拉(Leonard Euler)给出，被称为欧拉乘积(Euler product)，而更为严格的证明可以参考其他文献，此处从略。

显然当 s 为复数时，公式 (12) 给出的关系在 s 的收敛域 Re(s) > 1 上仍然成立：

其中 p 遍历所有素数。显然上述关系 (13) 将黎曼 ζ 函数与素数联系起来，并能够为研究素数的分布提供一定的线索。根据欧拉乘积公式 (13)，可以发现在级数收敛的区域Re(s) > 1上黎曼函数 ζ(s)不存在零点。为了进一步研究 ζ(s)函数的性质，欧拉对式 (13) 两边取对数：

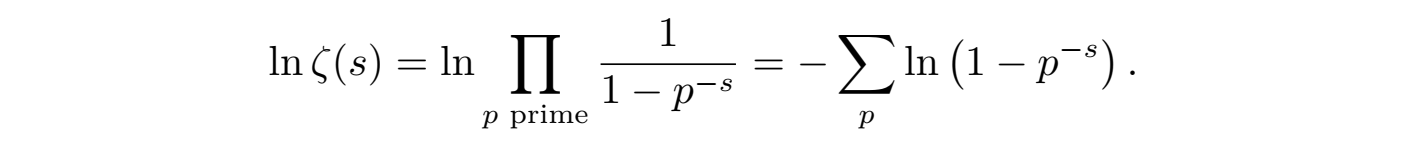
两边再对 s 求导数可得：

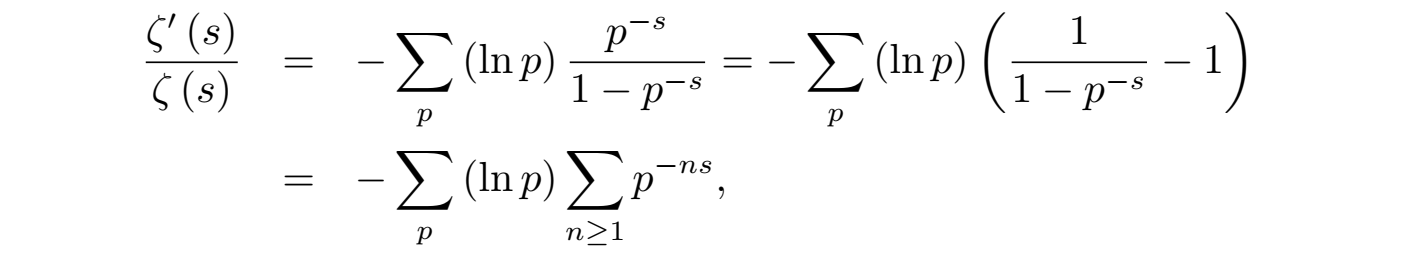
其中上式结果的有些技术细节此处省略，比如对无穷求和求微分的时候要从有限求和向无限求和过渡，以及利用了复数 z 的幂级数的收敛求和公式等等。这样我们可以定义：

这样最终就得到如下的结果：

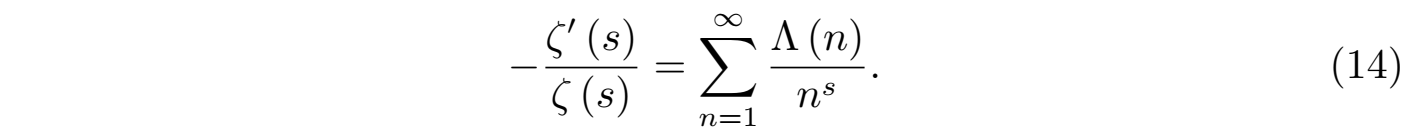
以上方程 (14) 中的函数 Λ (n) 即为冯 · 曼戈尔特函数(von Mangoldt function)，它的数学意义为：

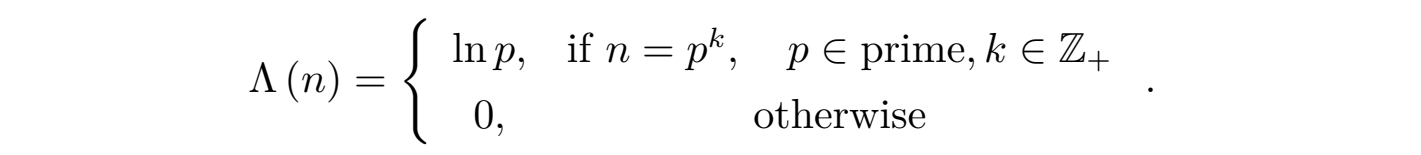
显然如果数 n 可以写为某个素数 p 的正整数次幂(如 p¹, p², ···)时，函数Λ(n) = ln p，其他情况都等于零。利用曼戈尔特函数 Λ(n) 我们定义如下的求和函数：

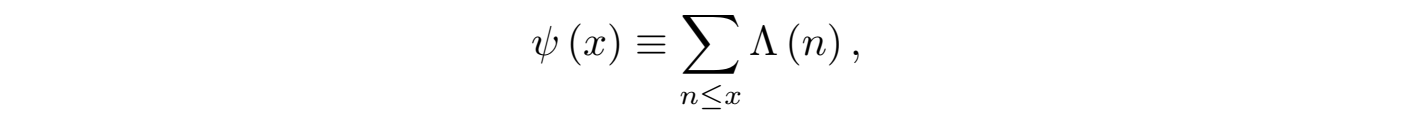
而该函数即为切比雪夫函数(Chebyshev function)。切比雪夫函数ψ(x)在研究素数分布函数π(x) 时具有重要的作用，比如切比雪夫证明 ψ(x) ∼ x 等价于素数定理 π(x) ∼ x/lnx 。曼戈尔特函数的求和函数ψ(x)是证明素数分布的核心桥梁，显然利用公式 (14) 黎曼将离散素数的分布与连续解析的黎曼ζ函数建立起联系，然后黎曼利用ζ函数的复积分性质得到了如下的结果：

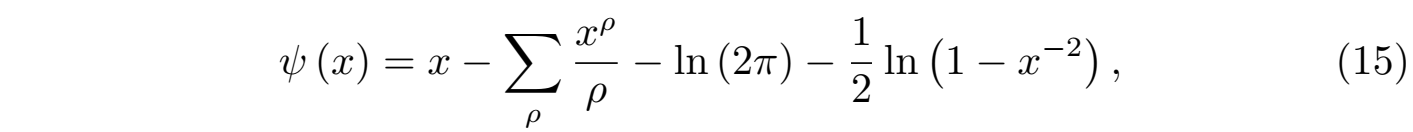
其中第二项求和的 ρ 遍历所有的黎曼函数 ζ (ρ) = 0 在临界带 0 < Re(ρ) < 1上的所有非平凡零点。显然公式 (15) 将素数分布的振荡误差归因于 ζ(s) 函数零点的贡献，这就是黎曼猜想和素数分布之间的内在联系。

4 黎曼函数的零点

所以黎曼函数的零点成了研究素数分布的关键，而黎曼猜想的焦点就成为：“黎曼函数 ζ(s)的非平凡零点全部分布在复平面 s = 1/2 + it 的直线上”。关于黎曼函数的零点，数学家和物理学家都非常关心和好奇，而关于黎曼函数零点的论文也是源源不断层出不穷，虽然直到今天该猜想确切的严格证明依然还没有被数学界彻底确认，但基于数值计算和其他领域的佐证结果，大多数人都认为黎曼猜是正确的。

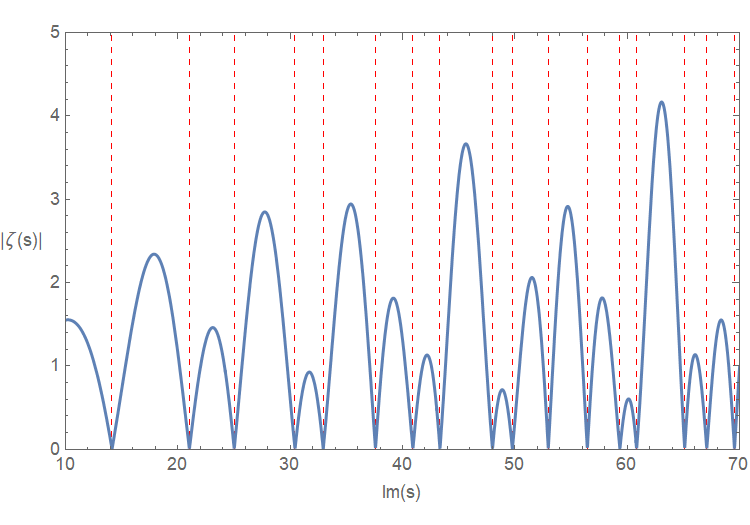
图1 黎曼函数绝对值|ζ(1/2+ it )|随虚部 Im(s) = t 的变化

首先，直接利用数值计算可以验证黎曼函数的零点分布，你可以在你的计算机上直接计算黎曼函数 ζ(s)的绝对值大小，就很容易发现只有在 Re(s) = 1/2时|ζ(s)|的值才能等于零(如图 1 所示)。其实这种利用数值计算进行黎曼函数零点测试的研究一直都在进行中，2025年初，通过分布式计算研究人员已经验证了前 50万亿(5 × 10¹³)个非平凡零点均位于临界线上(即对以往Gourdon-Demichel并行-分布算法的零容斥改进显著提升了计算效率)，而另一些研究人员结合快速Fourier变换降低了计算复杂度并达大大降低了单节点的计算开销，有望将零点验证的目标达到 10¹⁵ 个数量级。

然而通过计算验证零点只能推进黎曼函数零点的上限但并不能从严格意义上给出结论。所以有些数学家或物理学家通过其他方法去研究黎曼零点在临界线上的比例。从图 1 的曲线可见，黎曼函数绝对值|ζ(s)|在Re(s) = 1/2时，其值似乎不会出现过度的增长，应该存在一个上界(根据黎曼函数的性质，可以证明一个非常明显的上界 |ζ(1/2 + it)| < t^1/4，称为平凡上界，一般用指数1/4表示)。通过这个思路，2022年Paul Nelson首次解决了一般 L函数(黎曼函数属于此类函数)的亚凸性问题，即证明了对任意自守 L 函数，其临界线上的值增长均优于平凡界 1/4，所以任何优于 25% 的上界都称为亚凸界(subconvexity)，如2017 年Bourgain将上界降至15%。沿着这条道路，2025年Jonathan Maynard 等人在亚凸界研究中取得重要进展(进一步优化了 L 函数的上界)，他们通过改进筛法技术，证明了非平凡零点位于临界线上的比例达到了99.999%，而这一结果突破了此前由Mordell、Selberg 等逐步推进的99.99%的记录，数值计算让人类距离黎曼猜想的距离只剩下了最后0.001%。

如果我们继续观察图 1 就会发现，黎曼函数的零点在虚数轴上的分布就如同素数分布一样似乎是随机的，好像不存在任何规律。然而许多人对此也进行了研究，这就是零点分布的随机性研究。1973 年数学家Hugh Montgomery研究了零点对的关联函数(pair correlation function)，发现其形式与高斯幺正系综(GUE，一种描述复杂量子系统能级的随机矩阵模型)的特征值间距分布高度相似，如果将黎曼 ζ 函数非平凡零点的虚部归一化后，其间距分布与GUE随机矩阵特征值间距分布一致，这个发现被称为Montgomery-Odlyzko定律(law)，虽然2024年在高阶零点关联上也发现与GUE的统计结果一致，但目前它仍是一个基于数值统计的猜想而不是定律，显然这个猜想是建立在黎曼猜想基础之上的研究，是在对黎曼函数零界线上的零点进行统计其关联分析时发现的一个规律，虽然目前在10³²个数量级的零点分析都与GUE一致，但为什么一个纯数学对象(ζ 函数零点)与物理模型(随机矩阵能级间隔)能有这样一个精确对应？这是一个巧合，还是解析数论和量子物理(如量子混沌系统)之间真的存在某种联系？关于这个方面，一个更有量子物理味道的猜想是Hilbert-Pólya猜想，该猜想认为：黎曼 ζ 函数的非平凡零点ζ(1/2 + it)=0的虚部 t与某个无界自伴算子(厄密算子)的本征值一一对应。于是物理学家们似乎对此也产生了浓厚的兴趣，1999 年贝里(Michael Berry)与基廷 (Jonathan Keating) 提出哈密顿量H = x p + p x 的本征值ε_n可能对应于黎曼函数的零点的虚部 t_n ，被称为Berry-Keating 模型。这个方面的研究不仅在真实物理系统的谱实验上具有明确证据，例如在量子点、纳米颗粒等复杂量子混沌系统上测量到的能级分布符合GUE 模型(与黎曼零点分布一致)，而且后来的塞尔伯格迹公式(几何-谱对偶)与黎曼显式公式(零点-素数对偶)的结构极其相似，以及最近的一些研究工作(如2025年一篇论文提出了一种新的量子系统哈密顿量，其能谱能够较好对应 ζ 函数零点)都似乎在暗示素数分布与量子系统的谱可能真的存在某种统一的基本联系。

总之，无论沿着哪一条路前进，数学界普遍认为黎曼猜想的证明需要多领域深度交叉后带来的创新观念，能从更广义的角度上重构黎曼假设的数学框架，以期找到与其他数学分支的统一或联系，无论采用纯数学方法(如代数几何的方法)还是纯物理方法(找到严格的对应黎曼零点的哈密顿算符或调和厄密算符)，都需要新的思路或思想能将这两条看似巧合的道路联系或统一在一起。无论如何对黎曼猜想的持续研究极大地推进了解析数论、泛函分析与数学物理等领域的发展。