123. 庞加莱判据能识别四维空间中的球体吗?

Does Poincaré’s test identify spheres in four-dimensional space?

题记：你可以在一个甜甜圈上系一根绳子把它吊起来，但你却无法吊起一个球体，因为绳子总会从球体上滑下来。这个现象背后的数学原理可以用来可靠地判断3D空间中的几何体是否是球形物体。亨利·庞加莱(图1)猜想：这种判据应该也可以适用于更高的维度。这个猜想就被称为庞加莱猜想，现在已经被证明是正确的，所以这个科学问题的答案是：可以。

1. 引言

第123个科学问题就是庞加莱猜想，目前已经被数学家们彻底解决，现在叫庞加莱定理，所以本文的重点将不再是梳理问题的解决思路，而是介绍这个猜想是怎么变成定理的。首先美国克雷数学研究所网站对该问题有一个简单的介绍：1904年，法国数学家亨利·庞加莱提出一个问题，三维球面是否可以完全等价于一个单连通的三维流形？或者用更为流行的说法就是：是否每个单连通的三维闭流形必同胚于三维球面? 如果更数学化一些就是：若一个光滑紧致的三维流形M，其内任意简单闭曲线均可连续形变为一个点，那么 M 是否必然同胚于三维球面 S³? 这就是所谓的庞加莱猜想，现在它被看作是威廉·瑟斯顿几何化猜想(Thurston’s geometrization conjecture)的一个特例，已被俄罗斯数学家格里戈里·雅柯夫列维奇·佩雷尔曼(Grigori Yakovlevich Perelman) 在2004年前后最终证明。

图1 庞加莱猜想和证明三维猜想的佩雷尔曼

证明庞加莱猜想的过程犹如登山揽胜，每遇到一处艰难的险境都会出现锲而不舍的登山者为我们发现奇特的风景，最后俄罗斯数学家佩雷尔曼沿着以往登山者的脚步登上了顶峰。佩雷尔曼在完全证明庞加莱定理中做出了他独特的贡献，他的证明如同他个人的故事一样也充满了传奇的色彩。佩雷尔曼的证明是发布于论文预印本网站 ArXiv.org 上的三篇没有正式发表的论文给出的，他也因此被授予了2006年数学界最高奖：菲尔兹奖(Fields Medal)。这个奖在他身上也创造了三个奇迹：(1) 开创了以非正式发表的论文成果为依据颁发菲尔兹奖的先例；(2) 唯一一个拒绝受奖并拒绝领取任何奖金的人(包括克雷研究所为解决七大问题所提供的 100 万美元奖金)；(3) 唯一一个获奖后退出数学界的神秘人物。然而这三个奇迹也恰恰展示了科学界三个重要的东西：(1) 预印本对促进科学的发展尤其是颠覆性的科学发展具有重要意义；(2) 对纯粹科学的追求精神才是更值得尊重的科学品质；(3) 被认可而获得更高的荣誉不是科学家从事科学研究的动力，其实“数学就像旅行，任何人都有一睹胜景的激动和好奇”。咱回到猜想本身，佩雷尔曼的证明揭示出：每一个三维流形都是由一组“标准部件”构成的，而每个部件都由八种已被充分理解的几何结构组成，在这八种几何结构中，只有球体是单连通的。

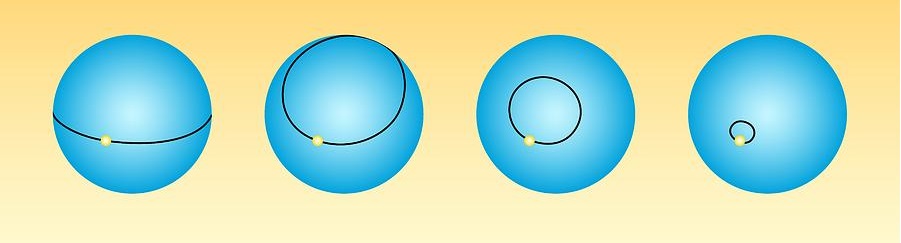
图2 球体表面闭合曲线的连续变化

以上对庞加莱猜想的简单解释并不能让我们真正理解庞加莱猜想的实际意义。所以克雷研究所网站又给出了一段进一步的介绍：如果我们用一根橡皮筋套在苹果表面，那么我们可以既不会扯断橡皮筋也不会脱离苹果表面慢慢移动它并使其收缩成一个点(见图2所示)。反之，若想象同样的橡皮筋以某种方式沿着甜甜圈表面适当方向拉伸，则在不破坏橡皮筋或甜甜圈的前提下，我们无法将其收缩成一点(见图3(b)所示)。我们通过这样的庞加莱判据发现苹果表面是“单连通的”，而甜甜圈表面则不是。大约在一百年前，庞加莱就已知道二维球面的本质特征正是这种单连通性，并由此提出关于三维球面的对应问题。

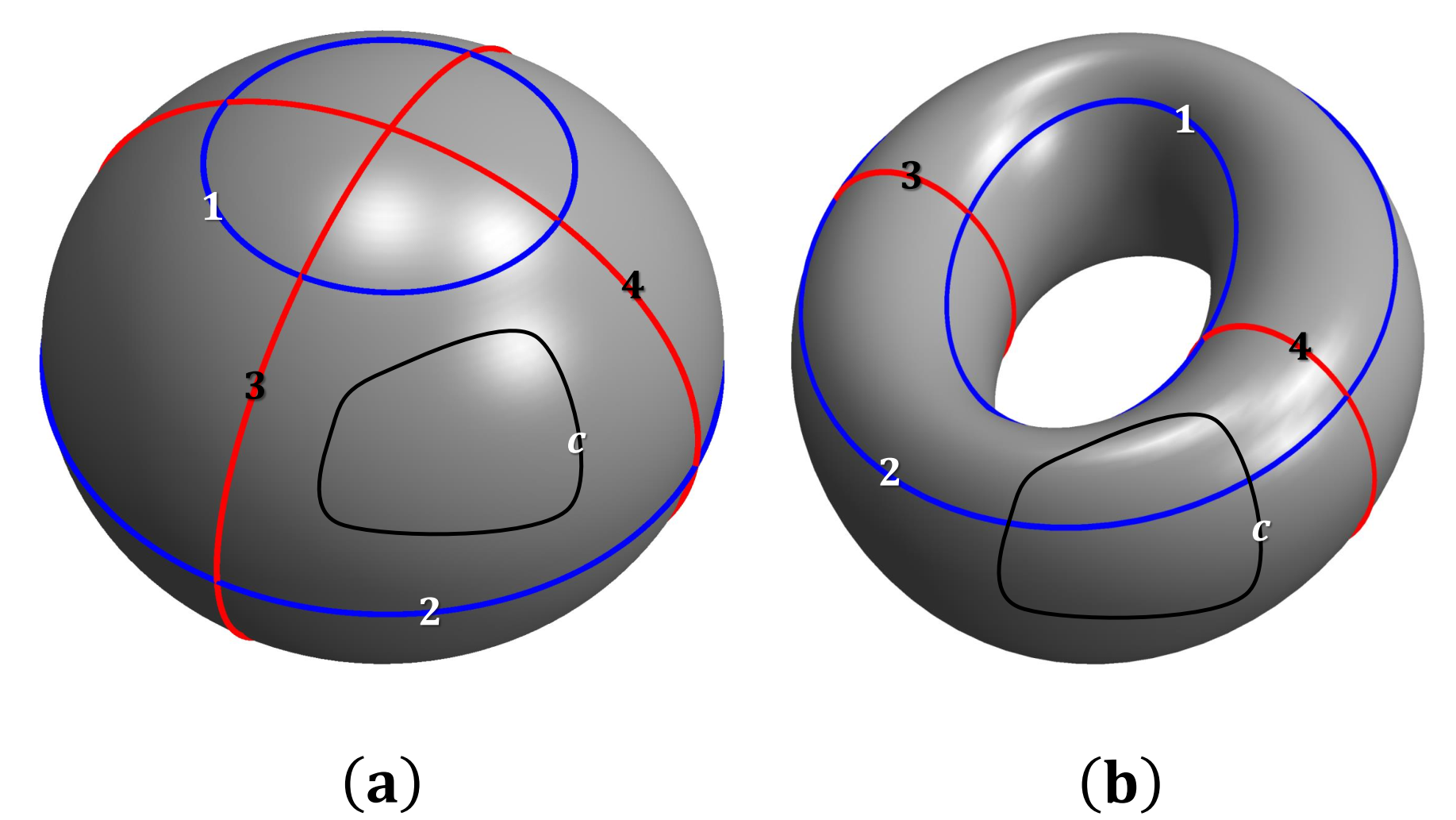
图3 (a)球体表面上的闭合曲线  (b)环面上的闭合曲线

最终证明庞加莱猜想的过程显示出三维问题具有超常的难度。从 1904 年亨利·庞加莱提出猜想，到格里戈里·佩雷尔曼在 2002-2003 年通过预印本网站 ArXiv.org 公布的解决方案，其间历经了近百年的时间，在这近百年中一维、二维(庞加莱)及五维以上(1961年由斯梅尔Stephen Smale证明，获1966年菲尔兹奖)、四维(1982年由弗里德曼Michael Freedman 证明，获1986 年菲尔兹奖)庞加莱猜想都先后被证明，只有三维庞加莱猜想显示出特殊的意义。庞加莱猜想通过斯梅尔的五维、弗里德曼的四维和佩雷尔曼的三维(称为菲尔兹奖三部曲)而最终被完全解决。而最后佩雷尔曼给出的证明是基于理查德·汉密尔顿的里奇流(Ricci flow)理论，并运用了齐格、格罗莫夫及佩雷尔曼本人在度量空间领域的研究成果。在佩雷尔曼发布的这些主要的arxiv论文中，他证明了更为广义的威廉·瑟斯顿的几何化猜想，而庞加莱猜想正是做为该猜想的一个特例而成立。

2. 庞加莱猜想三部曲

庞加莱猜想三部曲的证明过程非常精彩，显示了数学研究的思想魅力，值得我们去仔细追寻。首先，1961年斯梅尔独辟蹊径绕开三维问题，利用升维的方法首先解决了五维及其以上的庞加莱猜想。斯梅尔的主要贡献是他观察到高维流形(五维及以上)的额外自由度可规避三维中因纽结、自交等奇点所导致的拓扑形变障碍，从而为高维“拓扑手术”方法提供了“额外维度”的操作空间，也就是说五维及以上空间中，流形的额外维度允许通过光滑形变消除这些奇点(如自交曲线)，而在三维空间中此类操作因维度限制受阻而无法通过“手术”消除(即在余维n > 3即实维大于5的流形中，相交曲线可嵌入高维空间避免“打结”，从而可以光滑分离)。斯梅尔的核心证明方法是依靠配边理论(cobordism theory)与微分标准化，他利用微分拓扑与配边理论将流形分类问题转化为边界关系的可解性问题。他首先证明了单连通性与配边等价：若五维及以上闭流形M是单连通的(即任意闭曲线可收缩至一点)，则M与球面 Sⁿ配边等价(cobordism equivalence)。所谓的配边等价就是两个n维流形的并集如果可以作为一个n+1维流形的边界(即两个流形可以接起来构成更高维流形的边界，例如两个一维线段按边界接起来可以构成一个二维圆盘流形的边界，两个二维圆盘按边界连接起来可以构成三维球体的边界.....)，那么这两个流形配边等价。配边等价比拓扑等价弱，也就是两个流形拓扑等价一定配边等价，然而配边等价不一定拓扑等价。所以斯梅尔利用拓扑手术理论证明了：在五维及以上，如果两个单连通闭流形都配边等价于五维球面S⁵，那么它们拓扑等价，也就是斯梅尔的主要结论是高维单连通闭流形与球面配边等价，则必微分同胚于球面。

然而当维度低于五维，如四维流形时，四维流形的刚性(高维允许通过连续形变将微分结构规范化为球面，而低维的刚性阻碍此过程)导致斯梅尔的方法失效，四维庞加莱猜想需要新的思想或数学工具。为了解决四维问题，1983年弗里德曼将西蒙·唐纳森(Simon Donaldson)将规范场论的理论工具与四维拓扑的独特结构深度结合，开创了全新的研究方法。首先唐纳森通过研究杨-米尔斯方程(Yang-Mills Equations)的瞬子解(instantons)，他发现瞬子解空间的拓扑性质可用来刻画四维流形的微分结构。著名的杨-米尔斯场方程为(注意爱因斯坦求和规则)：

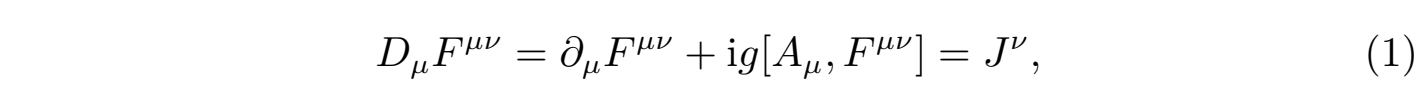
其中D_µ =  ∂_µ + i g A_µ为协变导数(covariant derivative)，F_µν = F^a_µν L_a为四维规范场的规范场强度张量：

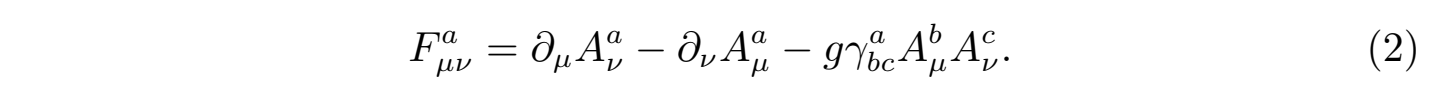
方程中A_µ = A^a_µL_a即为规范场(联络)，g为规范场耦合常数，γ^a_bc为规范场所属规范群G李代数生成元{L_a, a = 1, 2, ··· , dimG} 的结构常数：

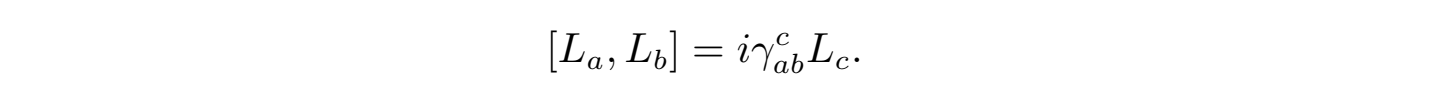
杨-米尔斯方程(1)的右边J ^ν四维时空广义流密度，它所决定的规范场强度F_µν的对偶场强度F^µν定义为：

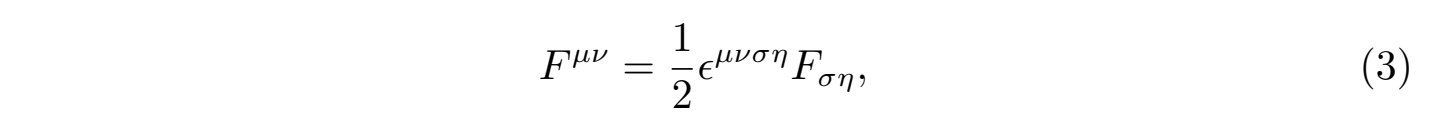
其中ϵ^µνση为为四阶全反对称张量，规定 ϵ⁰¹²³ = 1。瞬子解是四维欧几里德时空(Euclidean spacetime)中杨-米尔斯场方程的自对偶解(或反对偶解)，所谓的自对偶或反对偶解表示：F_µν = ± F^νµ，它是杨-米尔斯方程在欧几里德3+1维时空下有限作用量(finite action)S的局部极小解 δS = 0。杨-米尔斯方程的瞬子解具有非平凡的拓扑特性，可以用规范场的拓扑荷 Q (topological charge)来刻画，瞬子的拓扑荷 Q 是一个整数，它表示规范场在无穷远边界处的缠绕数(winding number)。

根据瞬子的拓扑性质，弗里德曼进一步证明：瞬子解的边界行为与四维流形的拓扑分类直接相关，尤其通过分析模空间的紧化性质，揭示了四维流形的同胚分类不依赖于微分结构(即发现了四维流形拓扑同胚和微分同胚的分离性，也就是存在拓扑同胚但微分不同胚的四维流形。唐纳森理论发现四维是唯一存在不同光滑微分结构而拓扑结构受控的维度)。他将规范场的卡斯米尔不变量(Casimir element)与流形的同调环结构关联，构建了四维流形的拓扑不变量。四维拓扑流形的特殊结构颠覆了“拓扑等价蕴含微分等价”的传统认知，凸显了四维拓扑的独特性(其他维度无此现象)，揭示了四维闭流形的同胚分类独立于其微分结构。弗里德曼与唐纳森合作建立了四维拓扑流形的分类定理：任何单连通闭四维流形由其相交形式(intersection form)的秩(奇偶性)和符号差(signature)完全决定，而四维庞加莱猜想作为特例(四维单连通同伦球面的相交形式必为偶型且符号差为零，则其必同胚于S⁴ )被涵盖其中。规范场论在四维拓扑中的应用，激发了量子场论与几何拓扑的深度交融(如威滕的拓扑量子场论)，弗里德曼通过物理学的规范场工具，破解了纯拓扑学手术在四维的僵局，他证明了单连通闭四维流形若同伦等价于S⁴，则必同胚于S⁴(同伦球面可以通过无限层状分解的拓扑手术技术构造出同胚)。揭示了维度对数学结构的深刻约束，而四维流形结构的独特复杂性——拓扑结构与微分结构的分离——至今仍是几何学的研究前沿。所以四维庞加莱猜想的证明依赖于相交形式的代数分类和改进的无限拓扑手术技术，揭示了四维结构独有的拓扑自由度与代数约束之美。

图3 几何体曲率的拓扑演化

下面我们重点来看庞加莱猜想的第三部曲：佩雷尔曼对三维庞加莱猜想“任何闭的单连通 (紧致无边)的三维流形必同胚于三维球面 S³”的证明。佩雷尔曼融合了几何分析、拓扑学和微分几何的前沿思想，核心工具是里奇流(Ricci flow)理论及其奇点分析理论，他通过微分几何构造“动态几何化”过程，将拓扑流形转化为均匀几何结构，其证明的核心是里奇流方程。里奇流是理查德·哈密顿(Richard Hamilton) 在 1982 年提出的几何结构演化方程：

其中g_ij 是三维流形上的黎曼测度(Riemannian metric)，而 Ric_ij 就是里奇曲率张量或里奇曲率(Ricci curvature)。里奇曲率是黎曼曲率张量的缩并(迹)，在局部坐标系下定义为：

其中R^l_ijk是黎曼曲率张量的分量，g^kl为度规张量的逆张量。我们知道流形上切空间“平行移动”的规则用联络(connection)来描述，而定义于联络上的曲率可由黎曼曲率张量来刻画，它反映了黎曼流形的内在弯曲程度，而这种弯曲程度从数学上则体现了流形上向量场在平行移动后的非交换性，其定义依赖于列维-奇维塔联络(Levi-Civita connection) Γ^k_ij，在局域坐标系下的具体表达式如下：

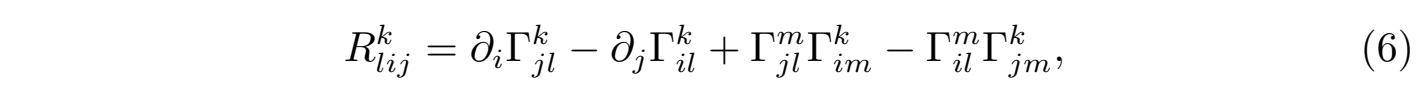
其中 ∂_i = ∂/∂x_i 为正常的局域坐标偏导数，而联络Γ^k_ij是流形空间二阶度规张量 g_ij的一阶导数(即三阶张量：Γ^k_ij=g^kl(∂_ig_jl+∂_jg_il-∂_lg_ij)/2)，那么黎曼曲率张量即为度规张量的二阶导数(四阶张量)，可见黎曼曲率张量由流形空间的度规决定，它描述了黎曼流形在局部偏离欧氏空间的程度，比如在弯曲空间中，向量沿不同路径平行移动后的方向可能不同(称为和乐变换)，如果把力场几何化后黎曼曲率则决定了沿不同曲线运动的场粒子其相对加速度的大小等等。理解了黎曼曲率张量，那么里奇曲率是对黎曼曲率张量的进一步粗粒化(求迹)，它表达了流形体积相对于欧氏空间的扭曲程度，也就是说里奇曲率的核心几何意义是描述流形 M 的局部体积dV_M与欧氏空间体积dV_E的偏差：

方程(4)表明：由于里奇曲率的存在二维流形上的黎曼度量会发生演化，即出现所谓的里奇流(Ricci flow)。这就如同热传导方程一样，温度梯度形成热流，热流的扩散传导最后得到一个均匀的温度分布，所以曲率张量会按照一系列扩散方程的变化而演变，高里奇曲率区域会收缩，低曲率区域会扩张，最终使流形趋向均匀曲率，这种演变趋势是将曲率均匀地分布在曲面上(如图3所示)。也就是初始不规则度规的曲率会通过时间演化变得均匀(正曲率趋于各处曲率一致的球面)，但这里存在一个问题就是：曲率演化中可能出现发散(奇点)，流形因此可能出现断裂，因此该问题的研究出现停滞。而佩雷尔曼通过改进里奇流方程和利用几何手术(geometric surgery)技术：当曲率在局部区域趋于无穷大(出现奇点)时，通过切割掉“坏”区域(如颈部的坍缩点)，并粘贴“帽子”(标准几何模型)，再继续演化，从而避免流形的拓扑结构因奇点而被破坏，从而维持流形的整体可控性。然而为了保证流形的整体可控制，必须能够证明这种对流形的几何手术是合理的而且能够确保手术过程可无限重复而流形不会出现崩溃。此处，佩雷尔曼利用熵泛函W(g, f, τ)(含时空权重的函数)证明其演化具有单调性：

条件方程(8) 为里奇流提供了“能量稳定性”，从而控制了流形曲率增长的速率，进一步证明了在里奇流作用下流形的κ-非局域塌缩定理 (no local collapsing theorem)：流形不会无限塌缩(体积会保持一个下限)，从而确保手术过程可无限重复而不崩溃。那么在流形不会发生崩溃的条件下，当某局域出现奇点时，通过对局域几何结构的分析，证明奇点邻域会渐近趋于某些标准模式，再结合拓扑流形分解与手术操作，最后将原始流形归结为有限个标准几何部件的组合，从而证明了任何闭三维流形可沿环面分解成若干片段，每个片段支撑 8 种标准几何结构之一，即证明了更广泛的瑟斯顿几何化猜想(Thurston’s geometrization)。然后通过里奇流和拓扑几何手术的极限态分析发现里奇流最终的演化结果是均匀的曲率空间(如球面)，而单连通性的要求又排除了其他几何流形，从而最终证明了三维庞加莱猜想。

3. 三维庞加莱猜想的总结

庞加莱猜想的证明显示了很多思想上的创新：(1)首先是它将静态拓扑问题转化为动态几何演化，通过拓扑结构的长期行为 (t → ∞)反推原始流形的拓扑性质，致使里奇流成为几何拓扑的核心工具；(2)流形演化中的奇点不是数学分析的障碍，而是流形拓扑结构的“探测器”，几何手术操作对应于流形的组合分解；(3)在流形的演化中，拓扑约束(如单连通)引导了流形几何结构演化的方向，并最终通过曲率均匀化实现拓扑结构的识别；(4)利用熵泛函约束与κ-非塌缩条件解决了哈密顿遗留的奇点控制难题，从而奠定了现代几何分析的研究基础。佩雷尔曼的证明被誉为 21 世纪数学的里程碑，其思想深远地影响了微分几何、拓扑学与数学物理的交叉发展，展现了“以几何动力学攻克拓扑难题”的非凡洞察力。