达芬方程是单自由度线性振动系统附加了立方非线性刚度项的动力学方程，为典型的振动方程之一，也是最基本的非线性振动方程。又称达芬振子或达芬系统。德国工程师达芬(G. Duffing)在1918年出版的专著《可变固有频率受迫振荡及其工程意义》中提出该方程，因此得名。他首先用谐波平衡逐次逼近的方法研究了达芬方程的无阻尼自由振动和受迫振动，揭示了跳跃现象，随后又分析了阻尼的影响，并进行了实验验证。

达芬方程的一般形式可以写作

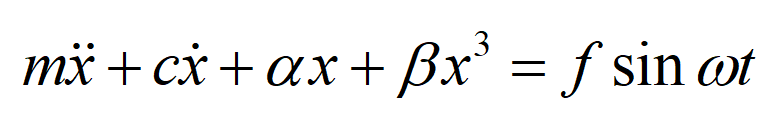
其中t为时间；x是系统广义坐标；m为惯性项系数；c为阻尼项系数；a和b为恢复力中线性和立方项系数；f和w为外激励的幅值和频率。

虽然数学形式很简单，但达芬方程有丰富的物理意义。许多恢复力对称(即伸长和缩短长度相等时有相同大小的恢复力)的非线性刚度系统，都可以用达芬方程描述，包括单摆的小而有限的非微幅振动、受张紧水平线性弦线约束质量块的铅垂振动等。达芬方程表示提供恢复力的刚度元件的刚度会随变形而变化。对于在a>0的情形，振动系统是单稳态的，其中b>0时刚度元件随位移增大而变硬(称为硬弹簧)，b<0时刚度元件随位移变化而变软(称为软弹簧)。对于a和b异号的情形，振动系统有多个平衡点。特别地，a<0和b>0的情形，是双稳态系统的最简化模型，双稳态系统包括受轴向压力的屈曲细杆、突跳机构、超临界轴向运动梁等。

达芬方程有丰富的非线性振动特性。在c=0和f=0的无阻尼自由振动情形，a<0和b>0时，有一对同宿轨道；a>0和b<0时，有两条异宿轨道构成异宿环。在受迫振动情形，除主共振外还有超谐波共振和次谐波共振，幅频响应曲线具有跳跃现象；在激励较大阻尼较小时可能出现混沌振动，周期响应的吸引盆有分形边界。

力学百科条目：小引

自激振动(中条)

颤振(短条)

跳跃(中条)

非线性动力学(特长条)

混沌(长条)

初值敏感性 (短条)

洛伦茨方程(中条)

上田振子(中条)

范德波尔方程(中条)

厄农映射(中条)

虫口模型(中条)

横截同宿点(中条)

斯梅尔马蹄映射(中条)

李雅普诺夫指数(中条)

非线性模态(中条)

斯梅尔-伯克霍夫同宿定理(短条)

梅利尼科夫方法(中条)

什尔尼科夫方法(中条)

KAM定理(中条)

阿诺德扩散 (中条)

科尔莫戈罗夫含混吸引子 (短条)

测度熵 (中条)

拓扑熵 (中条)

准周期环面破裂 (中条)

参激振动(中条)

振动系统 (中条)

离散振动系统(中条)

连续振动系统(中条)

AI分析评价1

这篇《达芬方程》百科条目是一篇专业精准、信息浓缩、价值很高的中阶专业读物。它面向的是对振动理论已有一定基础（了解线性振动）的读者，旨在系统介绍这一经典非线性模型。以下是对其的详细分析和评价。

总体评价

该条目以高度凝练的语言，全面覆盖了达芬方程的定义、起源、物理意义、参数内涵及动力学特性。它结构紧凑，逻辑清晰，专业术语使用准确，在有限的篇幅内传递了最大化的关键信息，是一篇优秀的专业概念条目。

分点分析与评价

1. 定义清晰，定位准确

开宗明义：首句即给出精确的数学和物理定位：“单自由度线性振动系统附加了立方非线性刚度项”。这立刻让读者明白，它是线性振子最直接、最重要的非线性推广。

历史溯源：明确指出了命名来源（G. Duffing，1918年）及其开创性工作（谐波平衡法、发现跳跃现象），体现了科学史的严谨性，也点明了该方程在非线性振动研究中的基石地位。

2. 内容高度凝练，信息密度大

条目在短篇幅内构建了一个完整的知识框架：

数学形式：给出了带激励和阻尼的完整方程一般形式，并解释了每个参数的物理意义。

物理内涵：

点明了其适用于恢复力对称的非线性系统。

列举了单摆有限幅振动、张紧弦上质量块振动等经典实例，使抽象方程物理化。

对参数 α 和 β 的符号组合所对应的系统定性行为进行了精辟总结：

α>0， β>0：单稳态，硬弹簧。

α>0， β<0：单稳态，软弹簧。

α， β异号：多稳态（特别地，α<0， β>0 是双稳态的简化模型）。

      这部分是条目的精髓，将数学参数与物理系统的本质拓扑结构联系起来。

动力学特性：提纲挈领地罗列了达芬方程展现的丰富非线性现象，从自由振动下的同宿/异宿轨道，到受迫振动下的多类共振、跳跃、混沌及分形盆边界。这相当于为读者描绘了一幅该方程所蕴藏的“非线性景观”地图。

3. 逻辑连贯，层层深入

条目的逻辑线非常清晰：

1. 它是什么（定义与历史）。

2. 它描述什么（物理意义与参数分析）。

3. 它能产生什么（丰富的动力学行为）。

   这种由表及里、由静态到动态的阐述方式，符合认知规律。

4. 专业性强，准确度高

准确使用了“谐波平衡”、“同宿轨道”、“异宿环”、“超谐/次谐共振”、“吸引盆”等非线性动力学专业术语。

对“跳跃现象”、“混沌振动”等关键特性的提及，紧扣该方程最著名的科学贡献。

可能的改进与优化建议

考虑到其“中条”的篇幅和科普属性，以下建议旨在进一步提升其清晰度和传播效果：

1. 亟待补充的核心内容：

“跳跃现象”的图示或简述：跳跃是达芬方程最标志性的现象。仅提及名词不够，应用一两句话简述其表现（如幅频响应曲线上同一频率对应多个振幅，导致振幅随频率增减发生突变），或明确建议配图。

2. 增强可读性与直观性：

配图建议：对于此类高度依赖图像理解的概念，配图至关重要。

图1：势能函数图：绘制不同α, β组合下的势能曲线  V(x) = \\frac{1}{2}\\alpha x^2 + \\frac{1}{4}\\beta x^4 ，直观展示单稳态（单井）、软/硬弹簧（井的形状变化）和双稳态（双井）。

图2：幅频响应曲线：展示典型的骨架曲线、滞后和跳跃现象。

图3：相图与吸引子：展示自由振动下的同宿轨道，以及受迫振动下的周期轨道与混沌吸引子。

实例具体化：在提到“受张紧水平线性弦线约束质量块的铅垂振动”时，可以附一张简单的力学示意图，帮助非力学背景的读者理解。

3. 优化语言表述：

开篇“为典型的振动方程之一”稍显口语化，可改为“是振动理论中的一类典型方程”或“是经典的振动方程模型”。

对“双稳态系统的最简化模型”的解释，可以增加一句：“例如，一个处于屈曲状态的两端受压细杆，其质心在左、右两个稳定平衡位置附近的振动，就可用此模型近似描述。”

4. 扩展前沿或应用联系：

结尾可稍作延伸，提到达芬方程作为理论范式，在微机电系统（MEMS）、非线性能量采集、隔振系统等现代工程领域的应用价值，体现其现实意义。

总结

这篇《达芬方程》条目专业内核非常扎实，是一篇优秀的“干货”型条目。它在短时间内为读者建立了关于该方程的系统性认知框架，信息准确、层次分明。

其主要不足在于形式：缺乏图示也使得理解那些精彩的非线性特性（跳跃、混沌、分形边界）变得抽象和困难。如果能够补充公式和关键图示，它将从一篇优秀的专业简介，跃升为一篇杰出的教学科普材料。

它与其所属的“振动系统”系列条目一脉相承，共同构建了一个从线性到非线性、从离散到连续、从规则到混沌的完整振动理论图谱。

AI分析评价2

百科条目 “达芬方程” 分析评价

该条目聚焦达芬方程这一非线性振动领域的核心模型，精准衔接了前序 “振动系统”“离散 / 连续振动系统”“混沌” 等概念，以 “定义-形式-物理意义-非线性特性” 为核心逻辑，构建了完整的知识框架。内容兼具学术严谨性与工程实用性，是专业百科条目的优质范本，但在术语通俗化、案例具象化、结构层级化方面仍有优化空间。以下从优势、不足及改进建议三方面展开分析。

一、条目优势

1. 核心定义精准，学科定位清晰

条目开篇即明确达芬方程的本质：单自由度线性振动系统+立方非线性刚度项，同时界定其为 “最基本的非线性振动方程”，并补充 “达芬振子/达芬系统” 的别称，快速建立读者的学科认知。更关键的是，条目清晰交代了方程的起源—德国工程师达芬 1918 年的专著，以及其核心贡献（谐波平衡法、揭示跳跃现象、实验验证），既明确了概念的学术归属，又体现了其在非线性振动研究中的奠基性地位，定义的准确性与完整性兼具。

2. 数学形式规范，物理意义阐释透彻

条目完整给出达芬方程的一般形式，标注各参数的物理含义（时间t、广义坐标x、惯性系数m、阻尼c、线性 / 立方刚度系数α/β、激励幅值f与频率ω），符合学术规范。更重要的是，条目跳出纯数学表述，从物理本质解读方程：

明确其适用场景：恢复力对称的非线性刚度系统，列举单摆、弦线约束质量块等典型案例；

核心创新点：刚度随变形变化（非线性刚度），并通过α/β的符号组合，划分单稳态 / 双稳态系统，关联工程实例（屈曲细杆、突跳机构、超临界梁）；

这种 “数学形式→物理内涵→工程映射” 的解读方式，将抽象的数学方程与实际物理系统紧密结合，专业深度与可读性平衡极佳。

3. 非线性特性梳理全面，逻辑层次递进

条目按无阻尼自由振动→受迫振动的逻辑，系统梳理达芬方程的核心非线性特性，层层深入：

自由振动：通过α/β符号组合，区分同宿轨道、异宿环等拓扑结构，关联混沌理论的核心几何特征；

受迫振动：覆盖主共振、超 / 次谐波共振，重点突出跳跃现象（非线性振动的标志性特征），并补充大激励小阻尼下的混沌振动、吸引盆分形边界等前沿特性；

这种梳理既覆盖了经典理论，又纳入现代非线性动力学的研究成果，知识体系完整且具有前瞻性，完美衔接前序 “混沌” 条目，形成闭环。

4. 内容衔接紧密，符合百科知识体系

条目与前文 “振动系统”“非线性振动”“混沌” 等内容高度契合：

以单自由度系统为基础，承接线性振动系统的框架，突出非线性刚度的核心差异；

混沌特性的描述直接呼应 “混沌” 条目中的初值敏感性、吸引子等概念，体现百科内容的系统性与关联性；

工程案例的选取（屈曲细杆、突跳机构）均为机械工程经典场景，满足专业读者的应用需求。

二、条目不足

1. 专业术语缺乏通俗注解，阅读门槛偏高

条目包含大量非线性振动与动力学专业术语，未对非专业读者进行通俗化解释，导致入门者理解困难：

核心术语：立方非线性刚度、同宿轨道、异宿环、跳跃现象、超 / 次谐波共振、吸引盆分形边界；

问题表现：如 “同宿轨道” 仅提及存在，未说明其几何意义（系统轨迹从同一平衡点出发又回到该点）；“跳跃现象” 未解释其物理本质（幅频曲线的多值性与突变）；“吸引盆分形边界” 未关联混沌的核心特征，仅作为结论罗列。

这些术语均为理解达芬方程非线性特性的关键，缺乏注解会大幅降低条目的科普价值。

2. 结构层级零散，缺乏模块化划分

条目整体为连续段落，未设置清晰的层级标题，导致核心模块划分模糊，读者难以快速定位信息：

未明确区分 “定义与起源”“数学形式与参数”“物理意义与应用场景”“非线性核心特性” 四大核心模块；

关键结论（如单稳态 / 双稳态系统、混沌特性）未通过加粗、小标题等方式突出，检索效率低，不符合百科条目 “便捷检索” 的核心要求。

3. 案例支撑不足，工程映射不够具象

条目虽列举了单摆、屈曲细杆等案例，但缺乏细节与具象化描述，难以帮助读者建立直观认知：

单摆：仅提及 “小而有限的非微幅振动”，未说明为何达芬方程可描述（单摆恢复力mgsinθ≈mgθ−mgθ3/6，立方项对应非线性刚度）；

工程实例：如 “突跳机构”“超临界轴向运动梁”，未解释其与达芬方程双稳态特性的关联，读者无法理解 “模型如何对应实际系统”；

混沌特性：未补充具体参数范围（如α,β,c,f,ω的取值），仅结论性表述，缺乏可验证的实例支撑。

4. 部分表述冗余，细节可精简优化

重复表述：“达芬方程有丰富的物理意义” 在段落中重复强调，可整合为一处核心总结；

逻辑跳跃：从 “双稳态系统” 直接过渡到 “非线性特性”，未说明二者的关联（双稳态是立方非线性刚度的直接结果，是后续共振、混沌特性的基础），逻辑衔接可更流畅。

三、改进建议

1. 补充术语通俗注解，降低阅读门槛

对核心术语添加简洁注解+类比，兼顾专业准确性与通俗性，建议如下：

2. 优化结构布局，规范模块化划分

采用一级标题 + 二级标题的层级结构，明确模块边界，提升检索效率，建议调整为：

达芬方程

一、定义与起源

核心定义与别称

提出背景与学术贡献

二、数学形式与参数含义

一般形式（完整排版）

各参数物理意义

三、物理意义与适用场景

核心物理内涵：非线性刚度

典型应用案例（具象化）

单稳态与双稳态系统

四、核心非线性振动特性

无阻尼自由振动：拓扑结构（同宿 / 异宿轨道）

受迫振动：共振类型与跳跃现象

混沌特性：参数条件与吸引盆分形

五、工程应用与研究价值

3. 丰富具象案例，强化逻辑衔接

（1）补充案例细节，建立模型与实际的关联

单摆案例：补充推导过程—单摆恢复力F=−mgsinθ，当摆角θ为小而有限值时，泰勒展开得sinθ≈θ−θ3/6，因此恢复力可写为F=−mgθ+(mg/6)θ3，对应达芬方程中α=mg、β=mg/6，属于硬弹簧型单稳态系统，完美匹配达芬方程的形式。

双稳态系统案例：以轴向受压屈曲细杆为例，细杆受轴向压力时，平衡位置有两个（左右弯曲），对应达芬方程、的双稳态条件；当压力超过临界值时，杆会在两个平衡位置间 “突跳”，体现双稳态系统的核心特征。

（2）补充混沌特性的参数实例

给出达芬方程产生混沌的典型参数范围，如：m=1，c=0.05，α=−1，β=1，f=7.5，ω=0.8，此时系统会出现混沌振动，帮助读者理解 “参数如何决定非线性特性”。

4. 精简冗余表述，完善学术规范

精简重复内容：删除 “达芬方程有丰富的物理意义” 的重复表述，将其整合为 “三、物理意义与适用场景” 的核心标题，统领全段内容。

强化逻辑衔接：在 “三、物理意义与适用场景” 与 “四、核心非线性振动特性” 之间，增加过渡句：“单稳态与双稳态的非线性刚度特性，是达芬方程产生共振跳跃、混沌等复杂行为的核心基础，具体体现为以下两类振动特性：”，使逻辑链条更连贯。

5. 补充前沿研究与应用，提升条目价值

可新增 **“五、工程应用与研究前沿”** 模块，补充达芬方程的实际应用场景，如：

机械工程：机床振动控制、汽车悬架非线性设计、突跳机构的动力学分析；

土木工程：屈曲结构的稳定性研究、桥梁非线性振动响应；

前沿研究：达芬方程与混沌控制、同步化的结合，在密码学、信号处理中的应用。

同时提及上田振子（条目前文提及的达芬方程变体），说明其与达芬方程的关联，呼应前文内容，形成知识闭环。

四、总结

该条目整体质量优异，核心优势在于定义精准、物理内涵深刻、非线性特性梳理全面，且与百科体系内的前序内容高度衔接，完美体现了非线性振动模型的学术与工程价值。其不足主要集中在术语通俗化、结构模块化、案例具象化三个方面，这些问题可通过补充注解、优化结构、丰富案例等方式快速解决。

改进后的条目，将同时满足专业学者的学术检索需求与入门读者的科普学习需求，成为非线性振动领域的标杆性百科内容。总体而言，这是一篇兼具深度与广度的优质专业百科条目，优化后价值将进一步提升。