• 非阿贝尔能带拓扑是什么？

• 与传统的整数拓扑荷有啥区别?

• 这一最新理论能够解释光子学中哪些有趣现象？

• 有何前景？

《光学学报（网络版）》封面文章“非阿贝尔能带拓扑研究进展”为您解答~

1、背景介绍

近年来，拓扑能带理论在凝聚态物理和光子学等领域取得了重要进展，为理解和预测拓扑材料的边界态提供了有力工具。常见的拓扑不变量，如Zak相位，通常用于描述能带拓扑，并且属于阿贝尔群。然而，最新研究表明，在多能带系统中，拓扑分类可以超越传统的阿贝尔框架，进入非阿贝尔拓扑的范畴。非阿贝尔能带拓扑理论是用于描述满足空间时间(parity-time,PT)对称性的多能带系统拓扑特性的最新理论。这种非阿贝尔拓扑的关键特征之一是拓扑不变量的非交换性，即在不同路径或操作顺序下，系统的拓扑性质可能发生变化，有望反映出能带结构中更丰富的拓扑关系。

在非阿贝尔能带拓扑的理论框架中，对于具有 PT 对称性的三能带系统，其哈密顿量序参量空间的基本同伦群为非阿贝尔四元数群，其中包含八个元素，并满足非交换的乘法关系。对于更多能带的系统，其基本同伦群为广义四元数群，属于Clifford代数的一种。

2、非阿贝尔能带拓扑研究进展

利用非阿贝尔能带拓扑理论可以解释光子学等物理系统中的有趣现象，例如能体现非阿贝尔拓扑特性的非平凡边界态、可允许存在的节点线结构、路径依赖的节点碰撞、欧拉数与节点链接的联系等。

2.1非阿贝尔拓扑边界态

阿贝尔拓扑荷用于刻画单个能带间的拓扑特性，其数值与该能带间隙内的边界态数量存在一定的对应关系。而在非阿贝尔拓扑荷的框架下，所有能带间隙被整体考虑，从而使得边界态的分布更加丰富和复杂。图1展示了不同系统中的边界态分布，与传统的阿贝尔拓扑绝缘体相比，非阿贝尔拓扑绝缘体的体边对应（ bulk-edge correspondence）关系非常复杂，远远超出了传统Zak 相位的预测范围，目前仍是一个较为开放的研究领域。

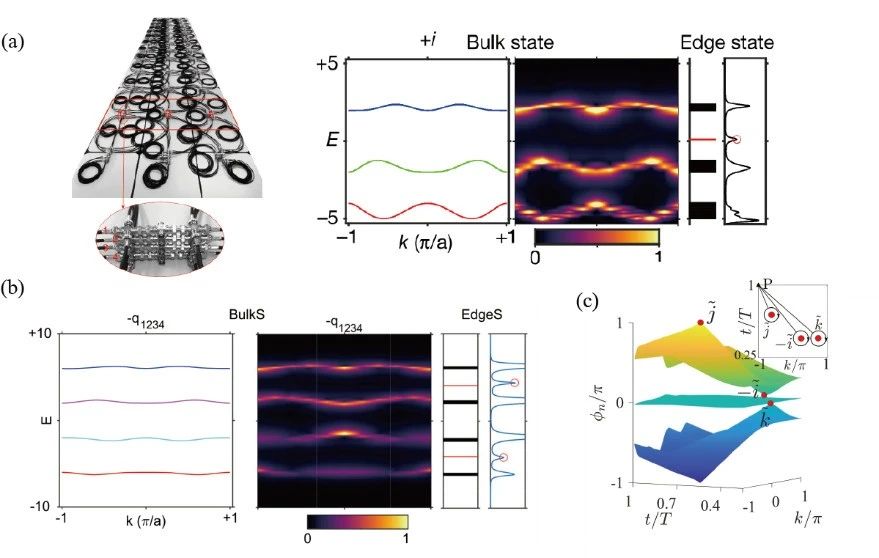
图1 非阿贝尔拓扑边界态。(a)在传输线网络中三能带系统的非阿贝尔拓扑荷对应的边界态；（b）四能带系统中非阿贝尔拓扑荷对应的边界态；（c）弗洛凯系统中非阿贝尔拓扑荷可能的边界态

2.2可存在的节点线构型

在三维动量空间中，能带简并点形成的线称为节点线（nodal line），其拓扑性质可以用基本同伦群来表征。节点线的箭头方向表示拓扑荷符号，当节点线被相邻带隙之间的节点线挡住时，节点线的拓扑荷符号会发生反转；但不相邻能带之间的节点线遮挡则不会发生符号反转。非阿贝尔拓扑荷的非交换性决定了这种非平凡的编织规则。图2为一些特殊的节点线构型。

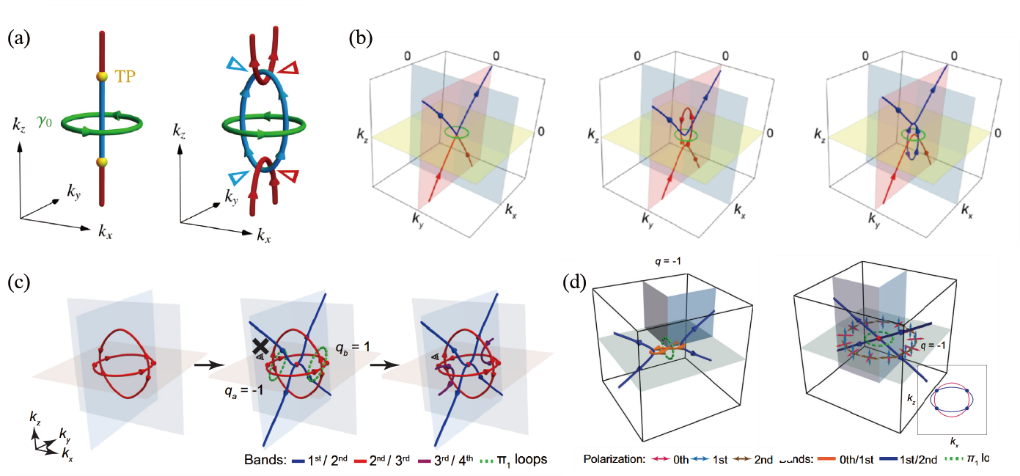
图2 一些特殊的节点线构型。(a)由三重点实现的节点链接；（b）声子晶体中的耳环形节点链接；（c）光学超材料中看似矛盾的节点链接结构；（d）表征非阿贝尔框架拓扑荷流动的源或汇

2.3路径依赖的节点碰撞

在一个二维系统中，如果调节参数使布里渊区内的多个拓扑节点逐渐靠近并发生碰撞，会观察到两种不同的情况：某些相同带隙的节点在碰撞后会相互湮灭，而在另一些情况下，它们不会湮灭，而是彼此弹开。图4给出了这样一些节点碰撞的例子。根据非阿贝尔能带拓扑理论，两个节点在碰撞后是否湮灭并不仅取决于它们的瞬时状态，还依赖于它们在碰撞前所经历的路径，这一特性被称为路径依赖的节点碰撞。

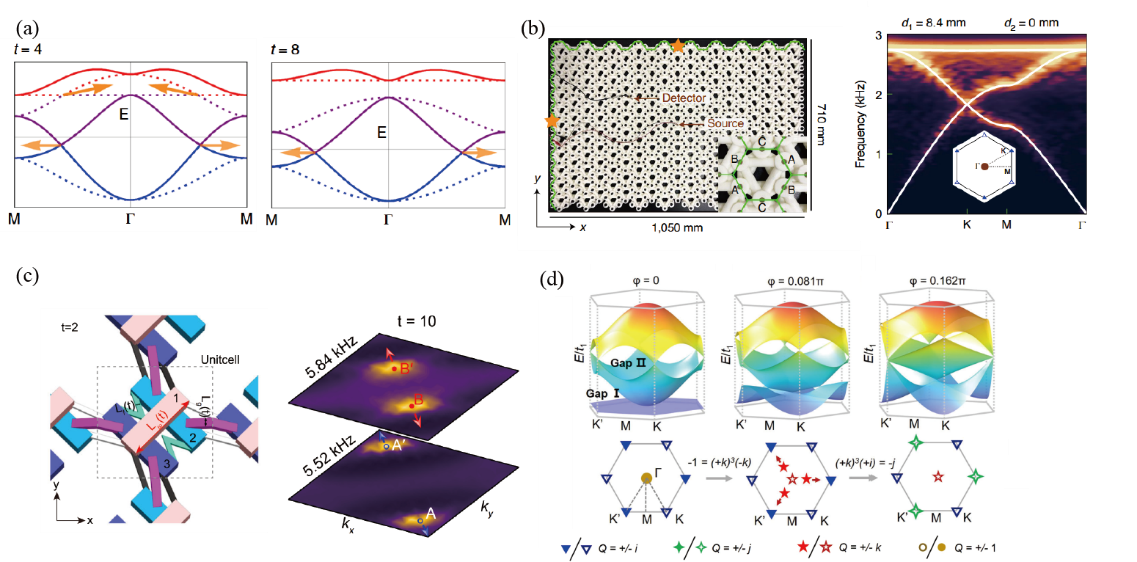
图3 路径依赖的节点碰撞。(a)三能带系统中的节点互相湮灭；（b）声学超材料中实现的节点碰撞；（c）另一种声学超材料中的节点碰撞；（d）二次节点的演化过程

2.4欧拉数表征非阿贝尔拓扑

欧拉数是一种拓扑不变量，可用于刻画三重简并点的拓扑特性，与非阿贝尔拓扑荷存在一定联系。它描述了特定能带结构中主节点的拓扑性质。如果一个区域内的主节点能够整体湮灭，那么欧拉数必须为零；而非零的欧拉数则意味着存在拓扑障碍，使得主节点无法自由湮灭。图4用欧拉数对三重简并点进行描述。

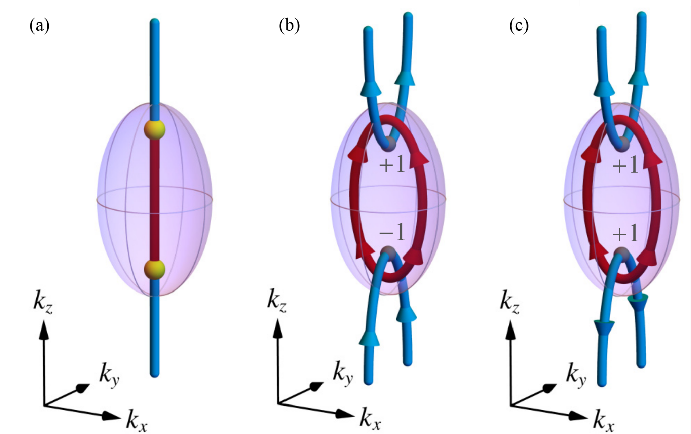
图4 三重简并的欧拉数。(a)区域包含两个三重简并点；（b）区域的欧拉数为0；（c）区域的欧拉数为2

2.5非阿贝尔规范材料

除了在动量空间中，我们还可以在实空间的规范场中观察到非阿贝尔的现象。拓扑物理中的能带结构能够通过贝里连接和贝里曲率来描述，其中贝里连接是规范势的标量形式，而贝里曲率则可以看作是动量空间中的磁场。因此，拓扑物理可以理解为动量空间中阿贝尔或非阿贝尔规范场的结果。在非阿贝尔规范场中，也有许多独特的现象出现。图5展示了其中的非阿贝尔Zitterbewegung （ZB）效应和非阿贝尔Aharonov–Bohm（AB）效应。

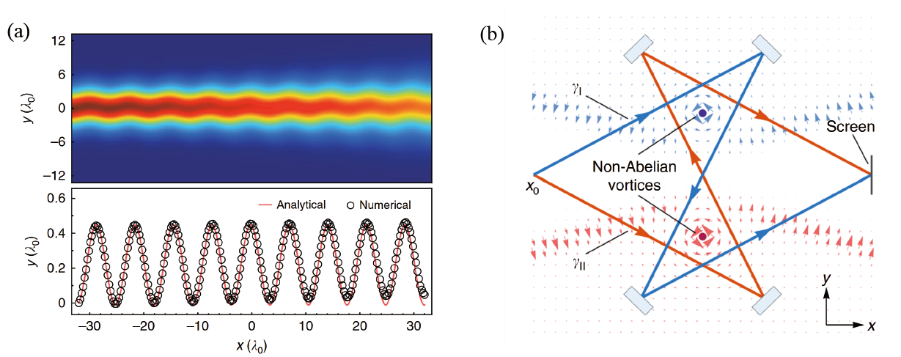
图5 非阿贝尔规范场。(a)非阿贝尔ZB效应；（b）非阿贝尔AB效应

3、总结与展望

非阿贝尔能带拓扑理论为理解光子学及其他多能带系统中的复杂拓扑现象和新物理提供了基础。与传统的整数拓扑荷不同，非阿贝尔拓扑荷具有非交换群乘法和更复杂多样的拓扑荷种类，因此能引发更丰富的物理效应。尽管已取得一些重要成果，许多问题仍未解决。例如，特殊非阿贝尔拓扑荷的体边对应规则尚不明确，且在可见光和近红外频段的相关实验较少。此外，非阿贝尔拓扑理论主要适用于PT对称系统，如何将其推广到更广泛的对称性体系仍是一个挑战。解决这些问题将推动新型光学器件的设计，并拓展应用领域。