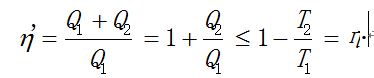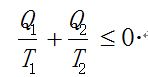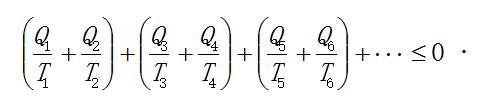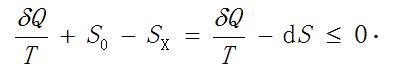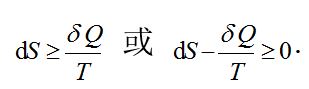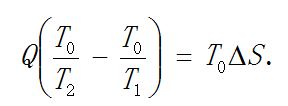博文
热力学的中学化教学纲要
|||
1. 热力学是一门专门研究两类永动机不可能实现的学科.
第一类和第二类永动机都永远不可能实现是人类宏观经验的总结, 具体表达分别为热力学第一定律和热力学第二定律(热力学第三定律是第二定律的补充). 热力学第二定律更具有时间(箭头)方向的特点是热力学的核心内容.
2. 不可能通过牛顿力学来解决热机的基础理论问题.
在近代物理的发展中, 可以说牛顿力学是最基本的学科. 但是1776年实用化的瓦特蒸汽机(又称热机)的出现, 涉及到的不是简单粒子之间的关系, 因此不可能通过牛顿力学来解决. 1824年法国年轻人萨迪∙卡诺对热机提出著名的卡诺定理, 成为建立热力学学科的第一个起步点.
3. 从“永动机”概念的提出到确定永动机不可能实现.
从16, 17世纪欧洲的近代化发展中就有人幻想能够造出一台不需要任何动力或其他外界物质的消耗、又能够自动作功的机器, 称之为永动机. 1775年巴黎科学院不得不宣布不再接受关于永动机的发明申请. 蒸汽机的出现就有更多人分别提出各种各样的所谓永动机的设计方案, 但是所有这些方案都经不住事实的检验. 实际上, 这已经是人类宏观经验的总结的雏形—永动机是不可能实现的. 卡诺在说明他的热机效率定理时, 也采用了这一认识.
4. 卡诺定理:
1824年萨迪∙卡诺研究蒸汽机时通过和水轮机的类比提出: 所有工作在同温热源与同温冷源之间的热机, 可逆热机的效率为最大. 卡诺定理的推论: 所有工作在同温热源与同温冷源之间的可逆热机, 其效率一定相等.这就是著名的卡诺定理, 也表明可逆热机的效率和工作介质无关.
5. 卡诺循环:
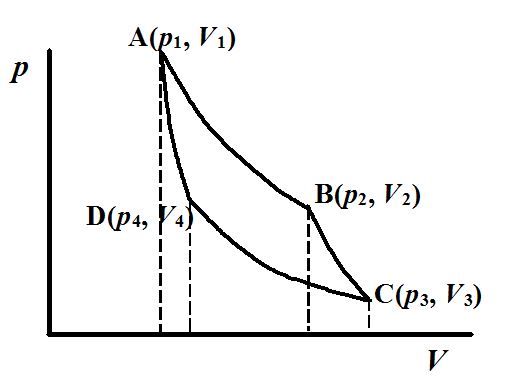
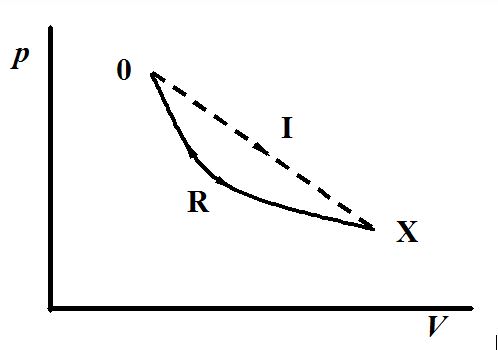
卡诺的可逆热机循环的四步过程(即等温膨胀、绝热膨胀、等温压缩和绝热压缩)可以用p (纵坐标压强) - V (横坐标体积) 图示方式来描绘, 参见图 1. 注意这种图示法中的实线一定是可逆过程.
图 1 卡诺循环的p-V图
(1). 等温(T1)膨胀. 由A(p1, V1, T1)到B(p2, V2, T1).
体系从高温热源T1吸热Q1并且全部转化作功W1.
(2). 绝热膨胀. 由B(p2, V2, T1)到C(p3, V3, T2).
过程中没有吸放热. 体系消耗内能对外作功, 温度从T1降低到T2.
(3). 等温(T2)压缩. 由C(p3, V3, T2)到D(p4, V4, T2).
对体系所作的压缩功W3全部转化成热Q2传给低温热源T1.
(4). 绝热压缩. 由D(p4, V4, T2)到A(p1, V1, T1).
过程中没有吸放热. 对体系的压缩功转变成体系的内能, 温度从T2升高到T1.
整个卡诺循环的四步完成后, 体系又恢复原来的状态, 体系对环境作功W就等于四边形ABCD的面积. 同时W= Q1+Q2, 其中Q2放热是负的. 由此可以看到热机从高温热源吸热Q1(吸热为正值), 将其中一部分热量对外作功W, 再将其余的部分热量Q2传给低温热源(放热为负值). 经过具体计算,最后热机的效率η就是W和Q1之比.
卡诺定理中的可逆热机的效率最高, 而与工作介质无关等, 也由此得到证明. 同时必须注意: 所有的计算和图1中T等都是以下要讨论的绝对温度.
6. 绝对温度:
1848年开尔文从理想气体体积收缩到零的外延方法得到了绝对温标.人们为了纪念他, 把绝对温标的单位就命名为开尔文, 并以K为单位符号来表示(绝对温度0 K = − 273.15 oC).绝对温度通常用大写的T来表示, 而通常的摄氏温度就用小写的t来表示.
7. 焦耳的热功当量:
1843年焦耳(James Prescott Joule, 1818-1889)通过大量实验证实: 热和机械功都是不同的能量形式, 它们之间存在着明确的定量对应关系, 一定量的机械功总是对应于一定量的热, 而和转变的方法或途径无关(4.184 焦耳产生1 卡的热). 后来就进一步发展成为能量守恒定律: 能量是不可以创造出来, 也不可以消灭的.
1847年焦耳在英国协会牛津会议上报告热功当量时引起很大的震惊. 因为当时开尔文已经把卡诺的理论引入了英国. 卡诺处理热机时就通过水轮机来类比的, 因此认为误热量通过高温到低温对外作功时, 热量和水轮机的水一样总量上是不变的.
8. 1850年克氏和1851年开氏等提出热力学第二定律:
1850年克劳修斯(Rudolf Clausius,1822-1888)在他的第一论文中, 首先就睿智地指出: 卡诺定理是正确的,同时指出: 卡诺把热量在高温到低温对外作功时, 说成是热量固定不变的是不正确的. 这就是以后所说卡诺的“热素论”错误. 克劳修斯还非常敏锐地指出: 需要一个全新的定律来解决. 这就是克劳修斯1850年提出的热力学第二定律表述: 从高温到低温的热传导是不可能自动反向进行.克劳修斯还特别把当时已经存在的“能量守恒定律”排列在前面称之为“热力学第一定律”. 1851年开尔文也提出了热力学第二定律的表述: 不可能从单一热源取热使之完全变为有用的功而不产生其他影响.此后, 开尔文还提出另一种表述: 第二类永动机是不可能得到的.当时也是仅仅针对不能从海洋取热作功的简单体系. 对只有自发不可逆过程的简单体系来说, 这些经典热力学的热力学第二定律表述是等价的. 但是仅仅适用于只有自发过程的简单体系.
9. 1865年克氏引入熵函数, 定量化地成功创建了热力学学科:
从卡诺定理知道, 任何热机的效率η’一定小于等于可逆热机的效率η, 因此
移项后得到
其中等式对应于可逆热机. 任何可逆循环过程都可以拆分成无数微小卡诺循环. 如果其中有可能包含不可逆过程, 就得到
于是克劳修斯就引入了一个新的状态函数S, 称之为熵(entropy). 并且把熵函数微小变化的定义为可逆过程中吸收的微小热量dQR和温度之比
其中三线等号表示定义, 下同.
引入了熵作为状态函数S以后, 对应于任何一个状态都可以有一个确定的熵值.
图2展示的微小循环过程中(可逆过程用实线和不可逆过程用虚线表示)
图2 循环过程的可逆过程和不可逆过程
由此就得到克劳修斯不等式, 也就是热力学第二定律的数学表达式.
对可逆过程可以采用等号. 对孤立体系(或绝热过程), 体系不吸收热, 所以热力学第二定律可以表述为熵增原理: 任何孤立体系(或绝热过程)的熵是永远不会减少的. (dS)iso≥ 0 或(DS)iso≥ 0.
式中dS表示体系的熵变. 下标“iso” 表示适用于孤立体系 (或绝热过程). 在经典热力学中, 等式对应于平衡体系或可逆过程, 而不等式对应于非平衡体系或不可逆过程.
10. 热力学的整体观和“时间箭头”:
熵增原理仅仅适用于孤立体系(或绝热过程). 在实际应用中, 遇到封闭体系和开放体系时就很容易犯错误. 因此在热力学中的整体观非常重要. 热力学的适用范围是大量(1023)粒子组成的宏观世界(或称自然界, 但是不包括我们日常经验中不清楚的宇宙中黑洞, 暗物质, 暗能量等部分). 因此, 把“体系的熵增”加上“环境的熵增”称为“整体熵增diS”:
diS ≡ dSsyst + dSsurr. |
|
仍然符合熵增原理的孤立体系要求, 于是就得到普适的整体熵增原理: 任何体系变化的整体熵增不可能为负.它的数学表达式:
diS ≥ 0. |
|
对热力学第一定律(能量守恒定律)也作同样的整体观处理, 就得到普适的整体内能守恒定律: 任何体系变化的整体内能的变化为零.它的数学表达式:
diU = 0. |
|
最后就可以发现, 整个宏观世界(自然界): 整体内能永远不变,整体熵值趋向于极大.必须注意, 这一特性可能是近代物理理论中唯一的, 因此热力学第二定律很早就被称为“时间的箭头”.
11. 热力学的整体观和“反应耦合”:
热力学的整体观非常重要. 就在1865年克劳修斯提出熵增原理的同时就明确指出: “第二定律, 在我所给出的形式中, 断定在自然界中的所有转变可以按一定的方向, 就是我已经假定是正的方向, 而不需要补偿地由它们自己进行; 但是对相反的方向, 就是负的方向, 它们就只可能在同时发生的正转变的补偿下进行.” 也就是说: 整个宏观世界体系的变化可以分为自发过程和非自发过程两大类. 因此, 热力学第二定律规定: 自发过程可以单独自己进行, [diS = diS1≥ 0]; 但是非自发过程就必需和自发过程的补偿(现在把它称为“反应耦合”)的情况下, 一同进行, [diS1> 0, diS2< 0 & diS ≥ 0]. 其中diS1和diS2分别表示自发和非自发过程的整体熵增, 而总的整体熵增是diS =(diS1+ diS2).
12. 热力学学科的完整基本分类系统:
显然, 这一热力学学科的完整基本分类系统(见图3)完全基于人类经验的总结, 当然仅仅适用于简单体系的卡诺定理也需要普适化成为扩展卡诺定理: 非耗散的能量转换是效率最高的充分必要条件. 注意: 非耗散的有效能量转换效率最高为100%. 不要和卡诺热机的转换效率式子相混淆.
图 3 热力学学科的完整基本分类系统
在这一热力学学科的完整基本分类系统中各个领域的应用实例也列在各自下方的园括号中. 同学们可以通过深入思考来慢慢领会.
13. 熵增的物理意义:
熵函数的量纲为J/K, 不是能量的量纲, 熵函数和温度的乘积具有能量的量纲, 孤立体系熵函数变化和温度(通常是环境温度)的乘积对应于能量的耗散. 实际应用中应该采用整体熵增和温度乘积TDiS的普适形式, 并且把TDiS称为耗散函数.
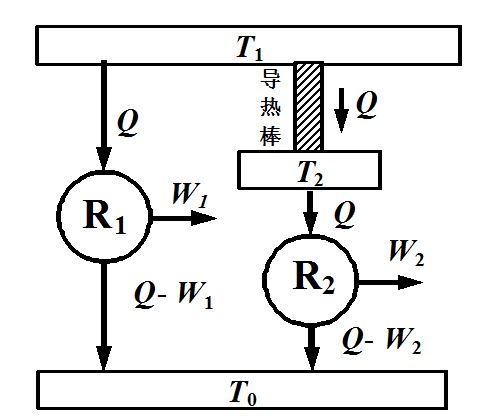
图4展示了热传导引起的能量耗散. R1和R2是两个可逆热机.
图 4 热传导引起的能量耗散
开尔文很早就据此证明: 相同的热量Q经过T1到T2的热传导, 对同样的环境温度T0作功能力减少了.
这就说明在孤立体系中热量Q从高温热源T1传到低温热源T2以后, 热量本身没有减少, 但是其中相对于环境对外作功的有效能(available energy)减少了T0DS. 或者说, T0DiS已经转化为无效能(unavailable energy), 这就是能量耗散.
14. 现代热力学的应用实例--低压人造金刚石:
通过以下三个反应式来表达:
1. 自发反应:
H* = 0.5 H2, (T激活 > > T, p ≤ 105 Pa) (DG1)T,p< 0, DiS1 > 0 . |
|
2. 非自发反应:
C (gra) = C (dia), (T, p ≤ 105 Pa) (DG2)T,p> 0, DiS2 < 0 , |
|
3. 反应耦合的总反应,反应式1和反应式2的反应速率比χ= r1/r2, 只要χ不是太小, 就得到:
C (gra) + χ H* = 0.5χH2 + C (dia), (T激活 > > T, p ≤ 105 Pa) (DG)T,p≤ 0, DiS≥ 0 . |
|
(DG1)T,p、(DG2)T,p和 (DG)T,p =[χ(DG1)T,p + (DG2)T,p]分别表示反应1、反应2 和总反应3的吉布斯自由能变化; DiS1、DiS2和DiS=(χDiS1 + DiS2) 分别表示反应1、反应2 和总反应3的整体熵增.因此完全符合热力学热力学第二定律.
15. 热力学中的一些派生的状态函数:
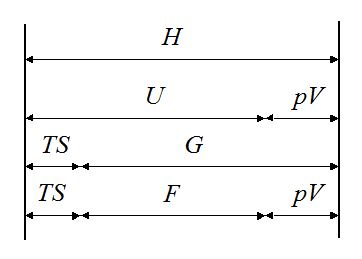
在今后的热力学学习中通常会遇到另外三个派生的状态函数. 它们的定义分别是热焓H ≡ U + pV, 等温等容自由能F ≡ U-TS和等温等压自由能(吉布斯自由能)G ≡ H-TS.
为了帮助记忆, 它们之间的关系可用图5的能量坐标来表示.
5 热力学函数间的相互关系
因为体系的变化经常在等温等压条件下进行的. 因此热力学第二定律也常常被写成吉布斯函数的变化的形式: (dG)T,p≤ 0; 简单体系[(dG)T,p= (dG1)T,p≤ 0]和耦合体系[(dG1)T,p< 0, (dG2)T,p> 0 & (dG)T,p ≤ 0]等. 等温等压条件下, diS=− (dG)T,p/T.
16. 总结:
对大量(1023)粒子组成的体系, 能量的两大基本特性--能量守恒特性, 和能量耗散及耗散最小化特性就归纳为热力学第一定律和第二定律.
热力学中最重要的理论基础就是第一类和第二类永动机都永远不可能实现是人类宏观经验的总结, 具体表达分别为热力学第一定律和热力学第二定律. 热力学第二定律更具有时间(箭头)方向的特点是热力学的核心内容.至今在任何宏观条件下, 包括生命体和生物进化, 都没有发现有第一类和第二类永动机的事实, 就证明了热力学理论具有普遍性和可靠性, 或者说这是热力学理论的真正严密性.
=====
对大学阶段的热力学教学可以直接参考我的2015年中文版和2016年英文版 "现代热力学(Modern Thermodynamics)."
https://wap.sciencenet.cn/blog-307912-1016177.html
上一篇:热力学课程教学创新第一人: 延边大学理学院郭振平教授
下一篇:改进的热力学中学化教学纲要