地球系统力学动力学（1）

李务伦

吉林省煤田地质局二零三勘探队

取名《地球系统力学动力学》成因

现行力学理论体系下地球动力学研究成果多若星斗，每一成果均是学者们以所能涉控理论，而形成的地球动力学理论，是新的知识结晶，都是值得学习和称道的。然而在这众多成果中，有一个奇怪的现象，太空中一切大的星体，为什么为球态？驱动为球态的动力是什么？可能笔者知识不够宽泛和认知的狭隘，发现对这一动力问题，并没有引起地质和地球物理学者们的重视、讨论与关注，这是一。二、地球是一个具有圈层球体，由内而外密度逐渐减小；“…硅铝层漂浮硅镁层之上”（注：巫建华等《大地构造学概论与中国大地构造学刚要  90页第二行》）。这些客观现象是通过地震资料的系统论证得到的成就，但为什么存在上述特征？仍可能是认知的狭隘，至今没有发现相应的理论给予论证解释。即便有解释，最多的提到的是早期物质分异，轻的上浮重的下降。但分异的数理根据是什么？如果说分异根据是浮力，但时下浮力的应用范围是流体，显然“…硅铝大陆漂浮在硅镁层上”叙述不当，然而硅铝大陆确实漂浮在硅镁层上，这又做何解释呢？可见时下浮力的内涵或理论有问题，有怎样的问题呢？没有回答。三、假如地球上所有物质均是如水一样是可塑的，地球的表层将是一个怎样的状态？这样陈述的目的是想说，物质的刚性或黏度是否是影响着地球构造运动的一种动力？

以上问题构成了地球动力学或一切星球的最主要内容，并依据众多的地球动力学成果，在此窃以为：应用于地球构造动力的基础理论存在着某种欠缺，正是这某种欠缺使得很多正确又有些缺陷的地球动力学成果，不能获得应有的对待和重视，例如重力动力学、对流动力学、自转动力学等。因此，将依据最基础的力学理论—万有引力定律：首先结合分子间作用，应用其解决地球为球形的动力及物质稳定平衡问题；二、接着解决浮力形成的数理根源问题；三、进而解决球层形成及物质稳定平衡的问题。这些最基本问题的解决，一、为许许多多地球动力学的成立提供理论基础，二、为建立地球系统力学动力学提供理论支持。

第一部分  星球为球体的动力与球内稳定平衡基本性质^[17]

这一章回答以下问题：1、根据分子间作用力和万有引力解决可塑物质为球的理论问题；2、给出球内外引力场强度计算公式；3、推出压力、引力位球内外计算公式；4、解答球内可塑物质稳定平衡问题，提出稳定平衡力和稳定平衡支持力的概念及计算公式。5、总结出均匀物质球内性质Ⅰ。

1、引言

    地球脱胎于星云物质，星云物质汇聚形成地球。这些星云物如何堆积？以什么形态堆积？是首先要回答的问题。当然现在人们都知道地球是一球体，但认识到地球为一漂浮太空的球体则源于天文观测。河南商丘古天文台已有四千五百多年，以此天文台观测算起，经过一千多年的长期不间断的观测，三千五百年前就意识到地球是圆（球）形的，并悬浮在空中旋转，地球在宇宙中小如微尘；到汉代中国人通过就提出“地圆学说”^[6-607]，是中华先贤持续的天文观测的成就与成果。但为什么是球体？而不是其它，如正方体、长方体等。在所能触及到的资料中，并没有看到让人信服的理论解释。可能有人会说，所有大的星体都是球体，地球当然也是球体，还解释什么，回答什么。在这里明确的说：这是一种非常错误的认知。也许有人可能说，为球的原因是重力，因为重力垂直地面指向地心，所以是球态的。对此对这种回答，只能说仅说对了一部分，而不是全部。根据已有学者们的众多地球动力学成果，马暑（2016年）对地球动力研究情况有如下见解^[8]：每个研究者“从某一个或几个方面的地质现象来分析，都由其合理性，但结合不同的地质现象进行分析时，就会矛盾重重”。陈志耕^[11]（1992）对影响比较大的地幔对流、地球自转、地球体积变化三类动力说，有“都还存在一些难以克服的困难问题”。这是为什么？巫建华教授^[7]（2008）认为现在还不是解决地球动力动力学问题的时期，仍需积累资料。马宗晋院士（2003年）对地球动力的发展认为^[7]：①能对全球构造特征及其空间分布规律、构造演化过程做出解释；②所依赖的动力因子既有足够的能量，其作用方式又能合理地说明构造变形场的特征；③符合物理学的基本原理和地球内部物质的物理-化学性质。通过分析众多学者们的成果异同和学者认为应有的发展思路，笔者确认为不准确清晰回答星球是球的这一问题，研究地球构造动力，恐怕永远是千人千面，永远争论不休。在已取得众多动力学成果的当下，今后如果想在地球动力学中想取得成绩，从理论上清晰回答星球是球，是当前首先必须认真直面的。仅是一种愚见，不当之处还望批评之！

在探讨星体为球形的理论前，先看一些图片。图1-1^[1]中左图为液体太空舱中的形态，从图中可以看出液体为球形，而该质量的液体在平的地面上，在不加边界条件限制的情况下，在液体黏度的规范作用下，形成基本为等厚的薄薄圆形一层。右图为太阳系各行星和太阳，它们均为球态。就连中国空间站点燃的蜡烛，火苗一改在地球表面的形态变为球形。

    Hayabu-sa2和OSIRIS-REx是日本和美国对小行星采样返回的两计划。在两计划执行过程中对小行星Ryugu和Bennu进行了拍摄，图1-2^[2]即是拍摄的两小行星图片。从图片中可以看到，两小行星都存在自转，上部小行星Ryugu椭球态稍差，下部小行星Bennu基本为椭球态，它们的组成均可清晰看到固体碎屑。在太空环境下，固体碎屑组成的小行星也为球体。固体碎屑的小行星为什么为球体？太空舱中液体和蜡烛火苗为什么为球体？几乎所有大的天体（星球）为什么都为球体？下面就从力学的最基本定律--万有引力定律和分子作用力，试探讨所有星球为球态的的动力数理根源。 

图1-1  太空舱液体球形(左）和太阳系太阳与各大行星（右）

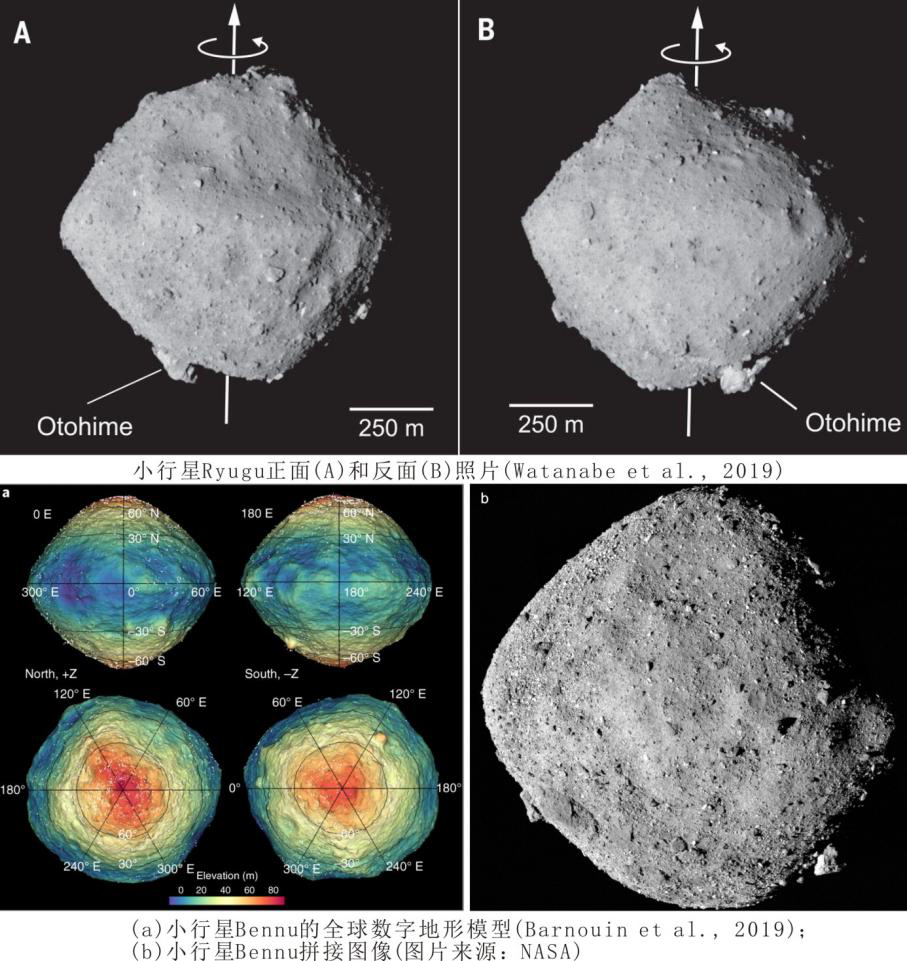
图1-2

在探讨星球为球态的数理根源前，择其我国古代文献的一鳞半爪，叙说一点古代中国先贤对天文学的贡献。1、位于河南商丘市雎阳区“阏伯台”是中国最早观星台，距今4500多年。2、《尚书》是中国第一部上古历史文件和部分追述古代事迹著作，保存了商周特别是西周初期的一些重要史料，其中明确记载“远古就有观象台、測星台”，并将天文观测到的“天象”记录其中。3、于两千多年的春秋产生“浑天说”。4、《张衡（78年-139年）浑仪注》“浑天如鸡子。天体圆如弹丸，地如鸡子中黄，孤居于天内，天大而地小。天表里有水，天之包地，犹壳之裹黄”。5、明·邢云路（约1549--1625）《古今律历考》有“五星去而复留，留而又退而伏、而期无失，何也？太阳为万象之宗，居君父之位掌发敛之权，星月借其光，陈宿宣其炁，故诸数壹秉于太阳，而星月之往来，皆太阳一气之牵系也”，是妥妥的太阳中心说，相互间的引力以炁代指。6、明·王徵（1571--1644）《奇器图说》^[10]卷一第一款和第四款中提出：“地球为球态，地球居于天体中心，引力线指向地心”。从上面的一鳞半爪，可以看出中华先贤，因农耕生产进步和需求，关注研究记录天体的演化，以服务农耕、发展农耕，提出宇宙模型--浑天说、地球中心说和太阳中心说；并以“炁”、“气”展示现代的“引力”，且“引力”的方向指向球心。在发展天文观测制定历法的同时，中国古代数学、物理、化学、医学等也循序渐进的进步并独步天下，而这一切的发展都有清晰的历史演进脉络记载。1671年法国建成欧洲第一个天文台，1675年英国成立第二个天文台，牛顿于1687发现了万有引力定律。

2、引力场理论和分子间分子作用力

2.1、引力场理论

万有引力定律表达如下：任何物体之间都有相互吸引力，这个力的大小与各个物体的质量成正比例，而与它们之间的距离的平方成反比。数学表达式为：

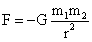…（1-1）

式中：G万有引力常数，G=6.67×10^-11 N·m2/kg2；m₁、m₂物体质量；r质量为m₁、m₂之间质心间距离；F引力，引力方向在m₁、m₂质心连线上

根据式（1-1），设其中一质点的质量为M，另一质点质量为1，两质点间的引力可表示为：F=-GM/r²。从式F=-GM/r²可以看成质量为M的质点，在距离为r的对单位质量的作用力。根据F=-GM/r²在质量为M的任一方向上距离为r的引力都相同。因而形成质点为质量M的引力场，这时的引力为便于与万有引力相区分，称为引力强度，用E表示。具体定义如下：对于任意质量为M质点，质点在距离为r的一单位质点p所产生的引力场强度^[3]6（或简称引力场，即一单位质点在p点所受引力）E为：

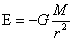…（1-2）

式中：G万有引力常数，负号表示引力场强度方向，引力强度的单位为N/kg

现代物理学研究认为^[4]：“引力场是暗能量和星体相互作用的产物。引力场中某一点的引力与暗能量的虚拟质量和星体的质量的乘积成正比，与该点到旋转中心的距离的平方成反比。”对于引力具体怎样产生，笔者难望项背，这里引述上述成果意在拓宽地球动力学的基础理论的范围，而下面的所有论述，仅能仅限于万有定律的范围。

有了式（1-2）就可以导出质点引力场的性质。根据式（1-2）可得出如下性质：质点引力场为球形场，同半径的球面上，引力强度处处相等。既然是引力场，根据式（1-2）可以求出引力线方程。根据矢量线所满足的微分方程^[5]15：

dx/A_x=dy/A_y=dz/A_z…（1-3）

A_x=E_x=-GMx/r³，A_y=E_y=-GMy/r³，A_z=E_z=-GMz/r³，将三式带入式（1-3）得：

dx/（-GMx/r³）=dy/（-GMy/r³）=dz/（-GMz/r³）…（1-4）

由（1-4）得引力线方程如下：

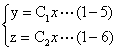
从式（1-5）、（1-6）可知是直线方程，且通过坐标原点，因而可知直线的斜率与任意半径为r球面经相同点的法矢相同，所以引力线垂直等引力强度球面，这是质点引力场的又一性质。

引力位是指在引力场中，单位质量质点所具有的能量称为此点的引力位，它的数值等于单位质量的质点从无穷远处移到此点时引力所做的功。而对于质点引力场，质点外任一点P距球心距离为r的引力位V，可由式（1-2）积分得：

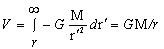…（1-7）

根据（1-7）式可以知道，质点的引力位为球面，引力位在同球面上的值处处相等。

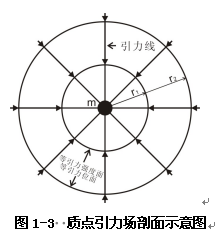
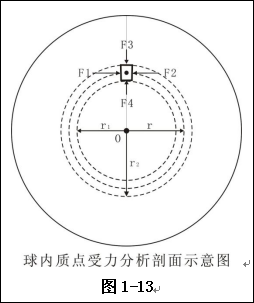
质点引力场定义式（1-2），引力场不但是球形场，也是以球心对称场，从而使得引力线球心对称，引力位也球心对称。于是可归纳出如下的质点引力场性质：1、质点引力场为球形，质点为位于球心上；2、所有引力线是通过球心的直线；3、球形引力场中，任意半径球面上引力强度值处处相等，方向指向球心；任意半径球面上引力位处处相等。这三条性质可用图1-3表示。根据前面的讨论，在质点质量为M的引力场中，引力强度为E（r），对于质点质量为m的物质，其在点质点引力场中所受到的引力为：

F=ma…（1-8）

式（1-8）中带入式（1-2），仍是万有引力定义表达式。

2.2、宏观量与微观量统计物理学理论简述

     分子的大小量级为10^-10m（10nm），一般都视为球形，这种球形有刚性和非刚性之分^[16][15]。科学的研究表明无论哪种球形，分子间的作用力距离量级约10^-8m，作用力范围较小。

统计物理学指出：宏观量是相应的微观量的统计平均值^[12]9。如密度、压力、速度、能量等宏观量。

①经典物理范围内，温度的微观意义：温度是物质热运动强度的量度，是分子不规则运动平均平动动能的量度。每一平动自由度的平动动能：

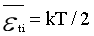…（1-9）

式中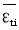：一个平动自由度的动能，k玻尔兹曼常数，T绝对温度，i自由度(下面相同符号不再标注)

②一个平动自由度动能与相应平动速度的关系：

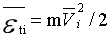…（1-10）

式中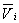：为平动一自由度速度，m粒子质量

③平衡态粒子数分布^[13]85

平衡态粒子分布的量子统计有三种：费米-狄拉克(FD)、玻色-爱因斯坦(BE)和介于经典统计和量子统计之间的麦克斯韦-玻尔兹曼(MB)统计。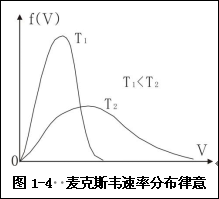

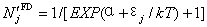
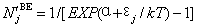
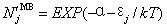
式中：α为常数，j能级，N能级分布

④麦克斯韦速率分布律^[13]60

理论研究知EXP(α+ε_j/kT)远远大于1，因本文非定量分析，所以认为平衡态时所有粒子分布，均遵守麦克斯韦--玻尔兹曼(MB)统计。粒子的速率分布律为：

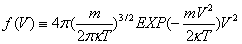…（1-11）

图1-4是式(1-11)式图示表达。

2.3、分子间作用力理论简述

分子间作用力分为斥力和引力两种，两分子距离相对较远时仅存在分子间引力，当两分子距离较近时又相互相排斥，如图1-7a、b^[14]所示。这两种分子作用力具有以下经验公式，分别为斥力公式f_斥(r)=λ/r^s(λ为常数)，引力公式f_引(r)=-μ/r^t(μ为常数)^[13]。引力将两个粒子拉近，斥力又避免靠的太近如图1-5所示^[13]。图1-5中虚曲线是分子间引力和斥力的合力曲线，实曲线是两分子相互靠近势能的变化。这一势能有伦纳德-琼斯势之称，一般表达式为U(r)=4ε[(σ/r)¹²-(σ/r)⁶]，式中ε、σ为常数，其过程相当于电子云相互交叠，粒子状态可更稳定^[13]20-22。

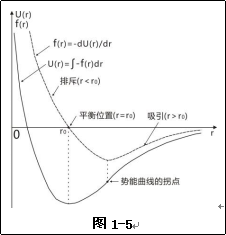
图1-5是一种非刚性球分子表述的分子作用力的一种情况，科学家还给出另一种非刚性球分子作用力成果^[16]，对于刚性球分子科学家也给出一种分子间力及作用势能研究成果^[15]。

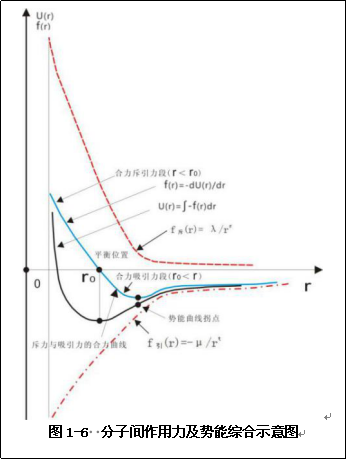
根据上面陈述的关于分子间作用力及势能的各种名称罗列，笔者认为它各表达了一类分子的分子间作用力和势能的具体情况。于是结合他们的成果，也为后面叙述统一，下面用图1-6表述分子间作用力斥力和引力及势能的一般情形。

上面归纳综合了已有能见到的文献各种分子间作用力的研究，分子间引力、斥力这二作用力作用范围较小，至于如何产生这种作用力不做涉及，而是在这理论框架下，以分子为球，各向作用力相同，分子的质心位于球心，作为下面研究的依据。分子作用力也满足微分方程式（1-3），分子作用力线方程与引力强度线方程相同，可见其性质与质点引力场性质相同。

根据上面对分子间作用力的讨论，当分子间引力和斥力合力为零时，两分子的相互接近取得的势能为最小，两分子间达到稳定互存，此时两分子质心最短距离为2r₀（见图1-7c），为后面便于分析问题，分子的半径约定为r₀。

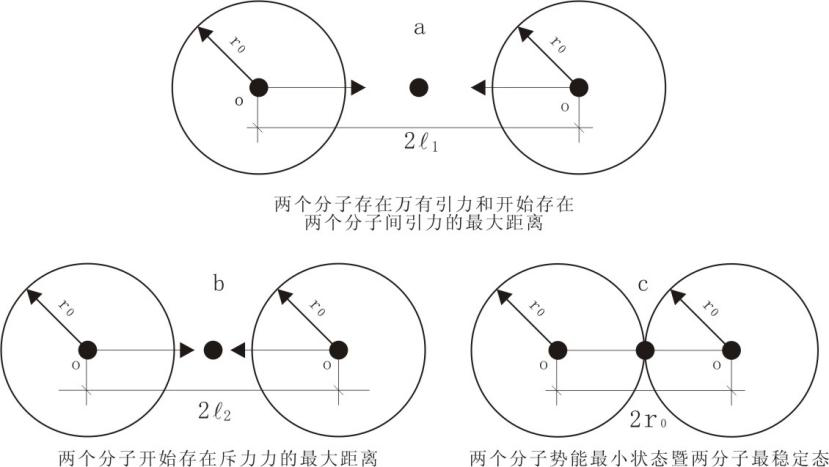
图1-7 两分子相互作用剖面示意图

3、多分子堆砌为球稳定系统的形成推演^[14]

荷叶上经常可以见到滚圆的小水珠，类似这种小水珠，常见的还有水银珠等，它们是怎样形成的呢？下面应用上面理论予以解答。

图1-7a表示了分子引力的最大作用范围；图1-7b表示了分子间斥力的最大作用范围；图1-7c中两个分子相互间处于最稳定状态-即势能处于最小状态。其体积是一分子的体积加一个直径和高度为分子直径的圆柱的棒状，质心位于棒状的中心（两分子的作用点上），该中心是新质点引力场的中心，2r₀是两分子质心的最短距离。由于分子存在质量m_e，根据万有引力定律，图1-7c中两个分子也存在质点相互作用力引力，作用力的方向在两分子质点质心的连线上；为与分子力形成的势能表述同步，对两分子万有引力引起的在相互靠近过程中，形成的势能也表述为不断减小，到图1-7c状态也达到最小，其数值表达式可根据式（1-7）计算得出为：-Gm_e²/(2r₀)。由于由于分子具有平动速度，处于不停的运动中，尽管两分子处于最稳定状态，但二分子并未形成刚体，并有新的质点引力场形成。

于是得出以下结论：两相同分子于空间中相互稳定的非刚体条件：一是两分子相切，二是分子间两种势能均达到最低。为方便后面应用命名为：二分子稳定定理。

图1-7c外部第三个同样分子出现于作用范围时，先做如下的受力分析：显然两分子对出现的第三个分子都分别有分子间的作用力和万有引力，当这个分子与其中一个较近，根据二分子稳定定理必定是优先与这个分子形成稳定状态，很快则与另一个分子也满足二分子稳定定理，形成图1-8（a）新的非刚性稳定系统。而新加入的分子的质心与图1-7c质心距离最小，并形成新的质点引力场。

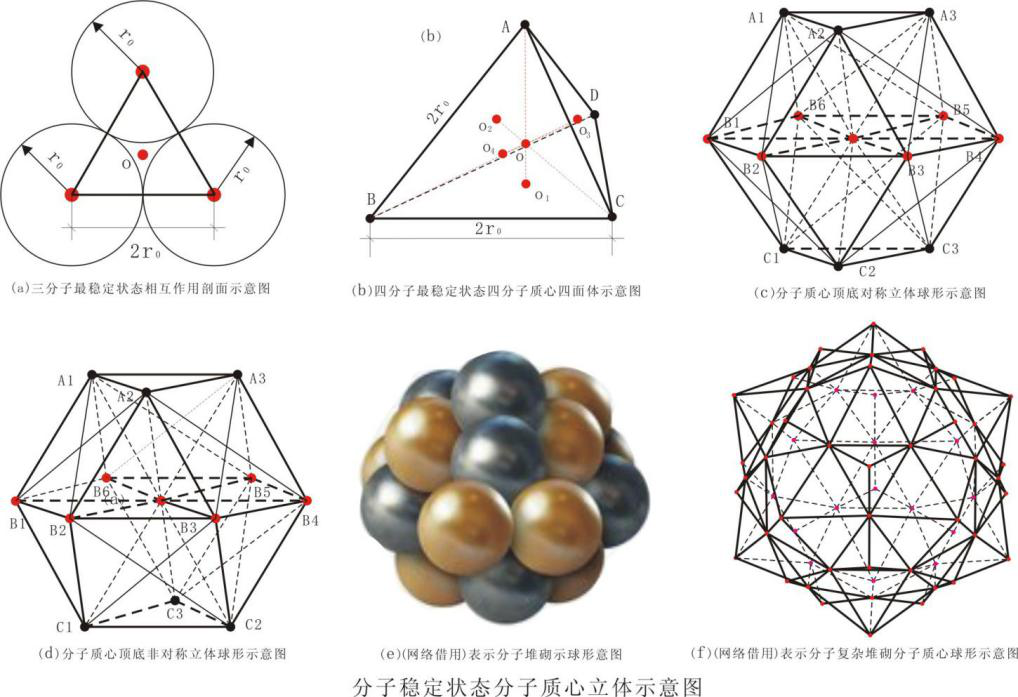
图1-8  分子相互作用堆砌示意图

图1-8（a）中三个分均处于最稳定状态，形成新的非刚性稳定新系统，质心位于图示的O点，同时形成新的质点引力场。当再有一个分子进入图1-8（a）稳定系统，根据二分子稳定定理，和上面对图1-8（a）形成的讨论，可知图1-8（b）是唯一选择。图1-8（b）中A、B、C、D表示了四分子的质心，任意两个分都遵守二分子稳定定理。此时图1-8（b）O₁、O₂、O₃与图1-8（a）中O的意义相同，根据几何与物理知识知，此时所形成的系统质心位于图示的O点。O点到A、B、C、D距离相等，因此A、B、C、D四点在半径为AO的球面上，四个分子在半径AO+r₀球面内，且新进入分子的质心与图1-8（a）的质心O距离最小。是一新的非刚性稳定系统，质心位于图示的O点，并有新的质点引力场建立。

通过上面的讨论，在二分子稳定定理基础上可得出以下推出：对于一个有多分子形成的非钢性稳定系统，任意新进入的分子，与之最近的三个分子质心，1、满足二分子稳定定理；2、非钢性稳定系统和新进入分子两者的质心距离最短。为方便后面的应用，命名为稳定系统稳定定理。

根据上面二分子稳定定理和稳定系统稳定定理，对图1-8（b）这一稳定系统想象一下，当有更多的同样分子进入这一系统，在前面推论的规范下，会是怎样一番情况？首先是图1-8（b）四个面的三个分子，分别会接收一个同样的分子，形成稳定新稳定系统。这一稳定系统新进入的分子质心与前述的A、B、C、D一样共球面且同心。这个球的半径增加一个r₀后的球面后，新入的四个分子都内切于该球内。这时的稳定系统，图1-8（a）示的三分子质心平面共有十二个。这样以来会有更多的的同样分子，与上同样进入形成更新的稳定系统。反复重复这一过程将会得到图1-8（e或f）的具有球形的稳定堆砌。而包含所有这些分子的球面，以图1-8（b）O为球心。

以上系统叙述了一种分子在分子间作用力和质点间作用力（万有引力），形成稳定堆砌球的可能过程，下面再叙述另一个可能的过程。以图1-8（b）的稳定系统为基础，十三个同样的分子首先形成图1-8（c或d）两个稳定堆砌十四面体结构。这两个稳定系统都以一个分子为中心，顶底各三个分子，中间七个分子在一个平面内。中心分子质心与其余十二个分子质心距离都为2r₀，均在分子间作用力和质点间作用力合力下等长度。这两个稳定系统遵守了前面的两个定理。这时的两个结构在半径为3r₀球面内，分子数达到最多，可划分得到图1-8（b）的稳定系统有八个，和有十四个外平面。当图1-8（c或d）外部有更多的分子，将在前面定理规范下，重复前面分子堆砌，随分子的增多，堆砌成的稳定系统的球形半径逐渐增大，也会出现图1-8（e或f）的稳定系统。

当图1-8（e或f）稳定系统随分子的再增多，稳定系统半径将有纳米级到百万级，再增多到毫米级，由于单个分子太小，人眼的分辨率所限，毫米级的分子稳定系统，以水为例，就可以看到滚圆的水珠。但水珠大到一定程度，在地球引力场下，水珠会变椭球，这一点也可在水银珠出现。这时上部物质根据（1-8）受力，使得底部物质稳定系统的力，因上部的重力对底部物质的做功，使得底部分级间势能升高，而使大的水珠、水银珠不再为正球。

通过上面的梳理推演，将类似荷叶水珠形成归为表面张力的叙述，应该没有触及问题的实质。因此觉得表面张力定义为：“分子间分子作用力和分子间质点引力的宏观表现”更为妥贴与妥切。

通过以上讨论，不难得出下面的结论：一切单一可塑物质，不论多寡在不受外力场影响情况下均为球，且只能为球。

4、均匀可塑物质球体内、外引力强度

    由于分子间作用力范围影响级别为10^-8m，与万有引力作用范围相比，前面由分子堆砌的球形集合体中，稍远就没有相互作用，但万有引力则不同，球内任意一分子无论与另一分子距离多远都存在相互作用。所以有分子组成的分子集合体，宏观上则只有万有引力的作用。分子堆砌的球形分子集合体，宏观表述上可用密度予以表述。下面讨论就根据引力场强度计算球内外引力场强度。

4.1  均匀球体外部引力强度

根据上面的讨论，可塑物质的展布为正球形，下面就计算正球形球内外引力强度。如图1-9所示，实心均质球外一点p的引力强度E可以通过以下步骤导出。设球半径为R且均质，密度为ρ，质量为M，OO₁=y，图示球外P点距球心距离为r。圆平面O₁垂直y轴，与平行于圆平面O₁的另一圆平面相距dy，平行于Z轴的AO₁B，O₁A=O₁B=k，相同质量质点A和B在P点的引力强度分别为dE＇和dE，方向如图示。对称的A、B两点在平行Z轴方向上合引力强度为零，所以半径为k的圆在P点平行平面OXZ的引力强度为零，圆平面O₁内，A点或B点对P点平行Y轴引力强度为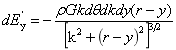，圆平面O₁内半径为k的圆环在P点平行y轴的引力强度：

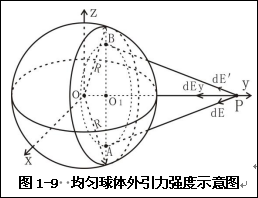
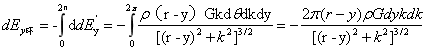
圆平面O₁在P点平行y轴的引力强度

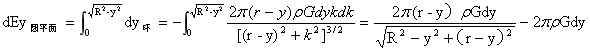
球O在P点平行y轴的引力强度

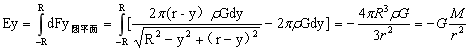
由于球的对称性，所以球外任意方向一点P，根据Ey又可写为：

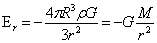  （r＞R）…（1-12）

由（1-12）式可得：一均匀球体在其外一点所产生的引力强度等于将其全部质量集中于球心所产生的引力强度。

4.2  均匀球体内部引力强度

高斯定理^[5]15是静电场的一基本定理，由于库仑定律和万有引力定律数学表达式相同，如果引力场中也引入通量，此时可称通量为引力通量，以Φ表示，引力场中的高斯定理可表述为：通过一闭合曲面的引力通量等于该曲面所包围的所有物质质量代数和的-4πG倍，即

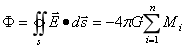…（1-13）

式（1-12）也可根据（1-13）得出。

如图1-9，球内部任意一点的引力强度，即可积分方法求出，也可根据高斯定理得出。根据高斯定理式（1-13），有下面的计算式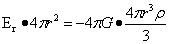：，解该式得：

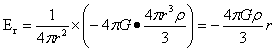 （r≤R）…（1-14）

上面式（1-14）表明：球内引力场，也为球形场，且内部任一点的引力场强度，等于将其以该点距球心为半径的球全部质量集中于球心所产生的引力强度。

   上面式（1-14）在球内引力强度均为连续函数，且根据公式所得出的球内引力线方程，与质点引力线方程与式（1-5）、（1-6）相同，同时与球外引力线相连续。也就不难得出球内同球面上任意点引力强度值相等，横向引力强度梯度为零，纵向引力强度梯度值相等。

    5、均匀可塑物质球内、外引力位

有了均匀球内、外引力强度，下面计算球内、外引力位。

5.1  均匀球体外部引力位

如图1-9，球外任一点P距球心距离为r的引力位V，可根据引力位的定义：“引力位是指在引力场中，单位质量质点所具有的能量称为此点的引力位，它的数值等于单位质量的质点从无穷远处移到此点时引力所做的功”计算得出。对于实心均匀球体，可由式（1-12）积分得出：

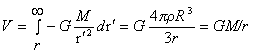…（1-15）

上述表明：等引力位值也为球形，一均匀球体或均匀球层在其外部一点所产生的引力位等于将其全部质量集中于球心所产生的引力位。

5.2  均匀球体内部引力位

半径为R，密度为ρ球均匀球内部引力位，根据引力位的定义：单位质量在引力场中做的功为引力位，于是可由式（1-12）和（1-14）积分得出：

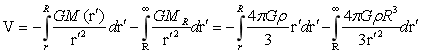
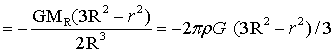   （r≤R）…（1-16）

上面（1-16）为连续函数，同一半且径上的引力位相等，也为球形。因此球内同球面上任意点引力位相等，横向引力位梯度为零，纵向引力位梯度相等。     

6、均匀可塑物质球内压力

关于压力，是指发生在两个物体的接触表面的作用力，或者是气体对于固体和液体表面的垂直作用力，或者是液体对于固体表面的垂直作用力。其定义为：垂直作用于流体或固体界面单位面积上的力。依据上述定义，可用以下两种方法求得。

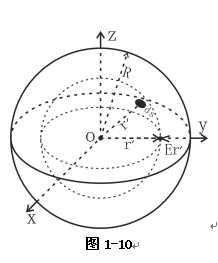
第一种算法：图1-10均匀球体，密度为ρ，半径为R，球内压力可根据式（1-8）做如下计算，下面就叙述这一过程：

如图1-10所示，在半径为r≤r′≤R的球面上上任取一面积微元ds，微元的高度为dr′，因此体积微元为dv=dsdr′，因此微体积微元的质量为：

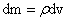…（1-17）

将（1-17）其带入（1-8）式，于是有：

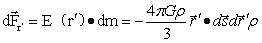…（1-18）

式(1-18)右侧是半径为r′的球对球外质点作用力，如果进一步变形则可看到是万有引力的表达式。（1-18）式两边同除以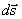就得微元对球面的压力dP，所以：

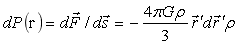…（1-19）

根据力的可加性，对（1-19）式从r到R积分，于是得到：

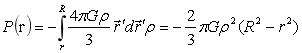…（1-20）

第二种算法：对于式（1-20）也可以通过以下方法求出。如图1-10所示，球内部压力P随从球表面到球内部的深度x加大而加大，满足如下方程：

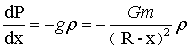…（1-21）

式中0≤x≤R-r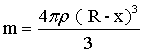，，，于是（1-21）变化为：

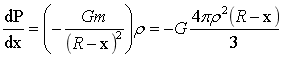…（1-22）

对式（1-22）积分可求得从最外球面到球内部半径为r的球面的压力为：式（1-20）。

以上两种球内压力计算方法，前者从理论的源头，在压力定义的基础上求取球内压力；后者则是根据重力场中的流体平衡方程求得，殊途同归。从（1-20）式知，均匀球内部压力随半径变化关系为抛物线关系，但在相同半径的球上，压力值确处处相等，横向压力梯度为零，纵向压力梯度在同球面上相等。

在我们的教科书中，流体静压力公式表达为p=-ρgh，其中g为重力加速度，h为高度。重力加速度g地球总力位法方向的导数，当地球不存在自转时等于引力强度。而在式（1-20）中：

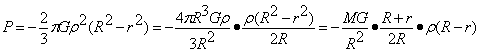
-MG/R²是球表面引力强度值，设R-r=h，-MG/R²=g。当R足够大，r又与R足够接近但又不相等，则(R+r)/2/R的值趋近于1，因此上式可写为：

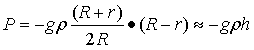…（1-23）

由此可见当h与R相比，几乎忽略不计的情况下，压力可以应用p=-ρgh计算。因此流体静压力表达式，仅是一种近似表达，但在进行地学问题分析时不应忽略。

7、均匀塑性体为球的基于引力位和压力的证明

上面虽从分子作用力和万有引力论述了可塑物质可堆砌为球，接着计算了引力场强度、引力位和压力。为了进一步说明可塑物质可堆砌为球的唯一性，下面做进一步证明。

证明一

如图1-11所示，半径为R的球，密度为ρ，球外有一图示的凸起，密度也为ρ，凸起对球形成的引力场认假设无影响。假设图1-11的情况可以存在，也就意味着图1-11处于各种平衡中。下面通过以下方面论证这一假设的不成立。

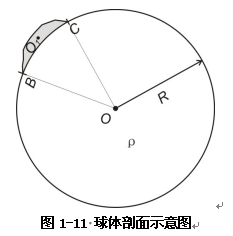
①假设存在力平衡。在图1-11中，弧BC之外的突起，存在一定的质量，在半径为R的引力场中，根据F=mE(r)，显然弧BC受力，此时的弧BC上任意点力不为零，而弧BC以外的部分所受的力，任一一点都为零，在半径为R的球面上存在不平衡，根据力的可加性，小于R的任意半径上，即图示的弧BC与O所围的范围内也存在与周边的力的不平衡，且大于周边。显然假设并不成立。

②假设引力位平衡。在图1-11中，根据引力位公式，球面上除弧BC外的引力位值都为M/R，弧BC上的引力位因上部的凸起，显然大于弧BC以外的引力位，存在着引力位的不平衡。同样在有弧BC和O所围的范围内也存在与周边的引力位的不平衡，且大于周边。显然假设并不成立。

③假设压力平衡。在图1-11中，根据压力公式，弧BC上的压力显然不为零，弧BC以外的地方均为零，在半径为R的球面上存在着不平衡；同样在有弧BC和O所围的范围内也存在与周边的压力的不平衡，且大于周边。显然假设并不成立。

综上，太空中的可塑性物质堆砌只能为球。

证明二

图1-12是太空中的一正方体，边长2R，密度为ρ。假如该正方体为可塑性液体，在太空中可以存在。下面通过以下方面论证这一假设的不成立。

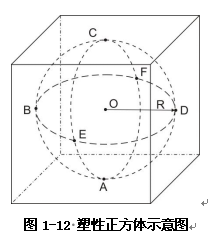
在图1-12的正方体内，根据几何学知道存在半径为R的正球体，该球体与与正方体各面的切点为A、B、C、D、E、F，球心O与正方体的质心重叠。假如在太空中可以存在正方体的液体，那么就意味着正方体处于平衡状态。

在图1-12中，根据高斯定理式（1-13）知，图示的正方体内球体的表面引力强度为式（1-12）。假设球外液体对该引力场无影响可以存在，也就意味着图1-12处于各种平衡中。下面通过以下方面论证这一假设的不成立。

①假设存在力平衡。在图1-12中，球外部分存在八个角，存在一定的一定的质量，在半径为R的引力场中，根据F=mE(r)，显然球面除A、B、C、D、E、F六点受到的外部力为零外，其余均不为零，即在球面上存在力得不平衡，相应的球内部也不平衡。显然假设并不成立。

②假设引力位平衡。在图1-12中，根据引力位公式球面上除A、B、C、D、E、F六点引力位值为GM/R外，其余部分引力位值均不为GM/R，显然球面引力位存在着不平衡；相应的球内部也存在着同半径上的引力位得不平衡，且大于周边。显然假设并不成立。

③假设压力平衡。在图1-12中，根据公式（1-20）或在（1-23），球面上除A、B、C、D、E、F六点压力为零，其余均不为零，在半径为R的球面上存在着压力不平衡；同样在内部同半径上也存在压力不平衡。显然假设并不成立。根据压力的面积特性，八个角的物质将向压力小的地方运移，直至成为球形。

综上三点，太空中的液体不能成为正方体，只能为球。

综上两个证明，结合前面分子堆砌为球的分析，可得出以下结论：太空中单一可塑物质为球体且只能为球。这一结论也适合多密度可塑物质为球，只不过是含球层的球，后面章节将一一讨论。

8、均匀可塑物质球体内部性质

经过前面的论述，已得出太空中可塑物质要保持内部所有质点的稳定、平衡，只能且只能为球的结论，也可归纳总结出以下球内性质。

性质1：球内任意点引力强度方向均指向球心，该点引力线为过球心的直线；

性质2：球内等引力强度面、等压力面、等引力位面均为球形。

性质3：球内同球面上：引力强度值、引力位值、压力值处处相等。

性质4：球内同球面上，任意点横向引力强度梯度、引力位梯度、压力梯度均为零；任意点纵向引力强度梯度、引力位梯度、压力梯度值相等。

性质5：球内引力线与各参数等值球面垂直。

性质6：球内任一点的各向应力值与该点的压力值相等。

以上六点球内性质是可塑物质为球的理论根本，也是球内所有质点处于稳定平衡的根源。这些性质应是星体为球的最基本、最根本动力理论，也应是星体内部稳定的根本的性质和标准。上述性质称为均匀物质的球内稳定平衡性质，简称球内性质Ⅰ。

9、基于均匀球内性质Ⅰ的系统性重力动力学略论

根据均匀可塑物质的球内性质Ⅰ，物质在太空中汇聚且稳定在一起，唯一途径是为球态。因此这些性质也就成了所有星球为球态的最基本、根本系统动力，所以形成重力动力学也是非常自然的，然而重力动力学与其它动力学，如地球收缩动力假说、地球膨胀动力假说、地球脉动动力假说、地球自转动力假说等确产生较晚（1987年，马杏垣）。从上面的讨论看，此处提出的重力动力学具有系统性。这一点以往的学者们也早已认识到。1^[6]、我国的学者章鸿钊、翁文灏，1916年主编的《地质研究所师弟修业记》，有地球系统运行动力根本上应为构造动力的观点，具体观点如下：“地质构造固与地质系统相关者也，也言其研究之序，则系统为先，而构造之后；考其进化之原则，系统为果，而构造为因……我国各时代之变迁与由是而及于地质构造之影响……”。2、1987年马杏垣等基于野外观测到的低角度滑脱构造-提出了重力滑脱构造^[9]，认为“重力作用可以影响一切构造变形，在岩石圈-软流圈中由各种因素引起重力失稳的动力系统中，会有足够的势能驱动全球板块的水平运动^注。根据大量重力测量成果证实，重力是地壳隆起、沉陷最主要的原因，就连滑坡、崩塌陷落等地质现象也主要是重力作用引起的^[7]。”从球内性质Ⅰ看，这是地球动力学真正的真知灼见。因此在众多动力学中重力动力学应称为地球第一动力学，地球动力学的核心动力学。这是因为，从均匀球内性质Ⅰ和众多学者的研究看，重力的作用是使得物质始终是：不断克服物质的黏度（刚性）或应力积累，使得物质形成最稳定的球形堆积！在这里提前提这样一个假设，假如所有组成地球物质均具有可塑性，根据球内性质Ⅰ，一切构造均不存在。地球假如不算气体的话，地球最外层是等厚的水圈，接着是等厚的硅铝圈，等厚的硅镁圈等等。从这一假设看，物质的黏度或刚性在地球动力学中起着不可忽视作用，也应是地球构造运动的一种派生性动力，本质仍是重力动力学。它起着延迟或迟滞重力等作用，而形成纵、横方向上应力积累。一旦黏度或刚性降低，应力得到释放，而从不同的角度，如重力、压力、势能、应力积累等，必造成未释放应力部分的各种构造运动动力学。

注：此处虽引用“会有足够的势能驱动全球板块的水平运动”，但不支持陆地大规模相互间移动由重力作用形成。

10、球内稳定平衡的受力分析^[18]

太空中一切可塑物质为球态，且所有质点都处于稳定平衡状态。然而具有怎样的受力，下面分两种情况分析之。

10.1 质点稳定平衡的受力分析

太空中单一密度可塑为稳定的球态，具有球内性质Ⅰ。球内任意质点（图1-13）处于处于稳定平衡状态，但又都处于球内引力场中，所以所有质点都会受力，根据式（1-8）和（1-14）受力为：

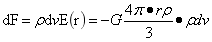
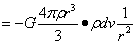…（1-24）

式（1-24）前半部分具有表达质点在引力场中的受力，后半部分表达质点和半径为r的球之间的相互作用力，后部是一种万有引力定律的表达。尽管存在这一力，但这一力根据球内性质Ⅰ并不使球内任意质点，无论多低的物质黏度都不会运动。下面进一步讨论不会运动的力学原因。

图1-13中在半径r的圆上存在图示的质点，该质点根据球内性质Ⅰ是稳定不动的。1、横向上在半径为r的圆上紧密的连续的存在图示相同质点，质点与相邻质点间存在图示的作用力F1和F2。根据作用力和反作用力原理，图示的质点又对左右相邻的质点施以相同力，从而使得半径为r的圆上横向上所有质点保持稳定，即F1=-F2。2、在图1-13的纵向上质点紧密相连，半径r圆上的质点上部与半径r₂的质点紧密相邻，相邻的质点对r上的质点作用力为F3，质点在引力场的受力dF为式（1-24），该二力作用到图示半径为r₁的圆上相邻质点上，根据作用力和反作用力原理，F4=-F3-dF，即图示的质点纵向上受到的合力为零：

F4+F3+dF=0…（1-25）

根据上面的分析，F4的大小取决于F3、dF的和，F4中去掉支撑F3的力后，便是支撑dF的支撑力F_支，由式（1-25）知F_支=F4+F3。F_支和dF是一对相互作用力：F_支=-dF。正是这一对力的存在，才使得位于球内任何位置的质点始终处于稳定平衡状态。物体浸于流体时，一旦物体与流体的密度相同，物体在流体中，物体可处于流体中任何位置。对这一现象可通过力的分析，也可分析出与上基本相同的表述。因此上面的分析，揭示了物体与流体密度相同时，物体可处于流体中任何位置原因的本质所在。

为了便于后面的叙述，根据上述分析，将图1-13中质点受力dF命名为质点稳定平衡力，其定义为：处于均匀球内引力场中的质点，质点所受到的不做功的力称为质点稳定平衡力；F_支命名为质点稳定平衡支撑力，其定义为：阻碍迫使质点稳定平衡不做功的力称为质点稳定平衡支撑力。这对力的形成，在微观层面看到的应是：分子间吸引力f_引(r)=-μ/r^t(μ为常数)使得分子间“亲密无间”；分子间斥力f_斥(r)=-λ/r^s(λ为常数)使得“亲密无间”分子间相互支撑，进而在宏观上使得质点间得以任意方向得以稳定平衡（注：该两式中r是分子间的距离）。

10.2 稳定球内划定区域的受力计算

通过以上的分析，形成了质点稳定平衡力和质点稳定平衡支撑力两个概念，下面运用这两概念计算划定区域的质点合力的稳定平衡力及区域的质点合力的稳定平衡支撑力。图1-14半径为r₀的圆就是均匀单一密度为ρ下半径为R大球内划定的区域，所示的剖面与x轴的夹角为θ，OO₁=l。

划定区域与外部大球内区域物质之间的相互作用力计算，可有两种方法：一种方法是根据万有引力定律进行计算；另一中是根据质点在引力场受力进行计算，这一方法又分大球球内引力场下和小球引力场下。

1、根据万有引力定律的计算

图1-14中小球内任意质点与小球外部大球内任意质点间，以如图1-14（2）中F点与O点为例，先计算小球与小球外的大球任意一质点的作用力，然后再计算小球外的大球所有质点的作用力的合力。F与O两点各自的质量分别为dm_小和dm_大，F与O两点距离为r，根据万有引力定律该两点间相互作用力：

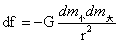…（1-26）

对式（1-26）固定O点，小球内所有质点对O点作用力，可通过对式（1-26）积分得到。根据图示的对称性，x、y轴上df的分量代数和都为零，所以仅计算z轴的分量代数和即可，由式（1-26）知z轴分量可表达为：

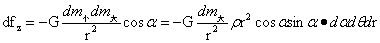
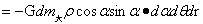…（1-27）

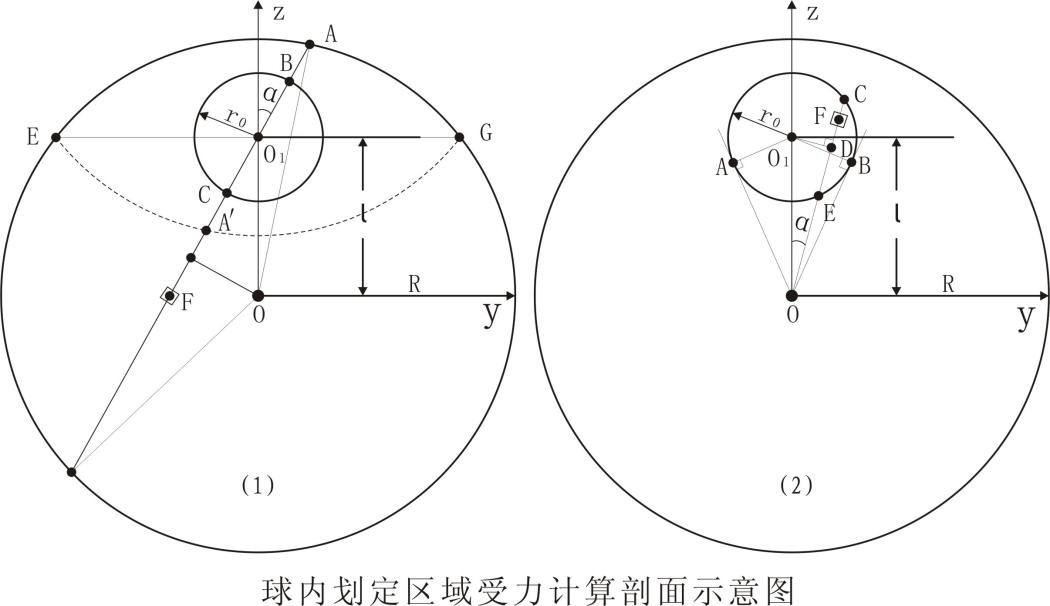
图1-14

式（1-27）积分各参数的取值：α∈[0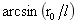，]；θ∈[0，2π]，r的取值通过计算OE和OC为：r∈[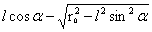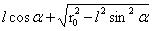，]，于是：

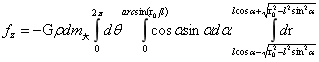
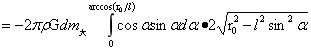
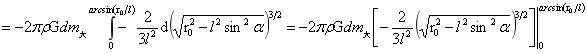
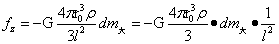∴ …（1-28）

这一式也可直接根据式（1-12）乘以dm_大得到。式（1-28）中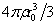为小球质量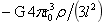，则为小球在小球外的引力强度。所以该式即是质点dm_大在小球引力场的受力，又是小球与球外质点的相互作用力。表达了小球与小球外大球内任意质点的相互作用力。于是根据该式对图1-14（1）小球与F点质点的相互作用力或小球引力场下F点质点受力为：

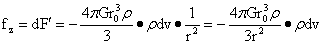…（1-29）

式（1-29）根据10.1的论述，可以看出该式即是万用引力定律，又是小球引力场下的表达。图1-14（1）中，AD上，O₁A=O₁A′，小球对BA、CA′这两侧上的对称质点的相互作用力相等，但方向相反。所以在计算小球与AD上除去BC后所有质点的合力时，仅需计算A′D段上的合力即可。根据图示的对称性，在x、y轴式（1-29）的分量代数和为零，于是仅需计算z轴上的力就可，在z轴上的分量为：

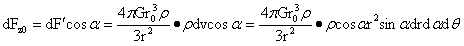
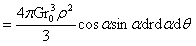…（1-30）

式（1-30）各参数的取值范围，α∈[0，π/2]；θ∈[0，2π]。AO₁和DO₁通过计算分别为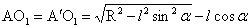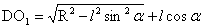：，。所以r的取值范围r∈[，]。

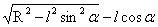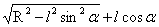对（1-30）式作如下积分：

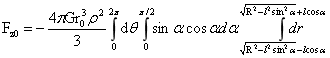
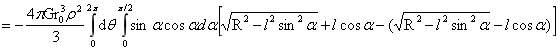
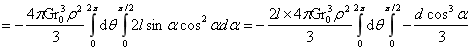
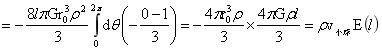
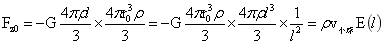∴ …（1-31）

式（1-31）表达了小球与外部大球内物质间的相互作用力，解出了划定区域内的稳定平衡力。而表达式前半部，表达了小球在大球球内引力场下，小球内所有质点受力，合力作用点在小球球心O₁；后半部分则表达了半径为r₀的小球与半径为l球间，存在两球交汇的万有引力定律形式的相互作用力，力的相互作用点在O和O₁上。

式（1-31）所表达的力，是划定区域内所有质点与大球除去小球后的大球所有的质点间相互作用力。这一力并不能影响大球内任何质点的稳定与平衡，符合球内性质Ⅰ，与质点稳定平衡力具有相同的特征，所以命名为稳定平衡力。既然有了有了稳定平衡力，根据前面质点稳定平衡力与质点稳定平衡支撑力是一对相互作用力，所以小球底部存在对小球的稳定平衡支撑力，其表达式为：

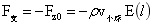…（1-32）

2、引力场下的计算

前面用万有引力推导出稳定平衡力和稳定平衡支撑力，下面给出引力场下计算方法。图1-14（2）大球内引力场下，质点F的受力表达式为式（1-27）。根据前面的分析，仅需计算式（1-27）在z轴的分量的和就可计算出稳定平衡力，所以z轴的分量为：

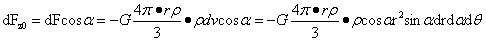…（1-33）

式（1-33）各参数的取值范围与式（1-28）相同，于是对（1-33）积分：

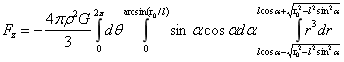
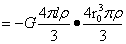…（1-34）

式（1-34）的积分过程见附录2。式（1-34）与式(1-31)相同，这就用引力场又求出稳定平衡力。

对于图1-14小球位置换为旋转球台，旋转球台球心也在O，旋转球台球外半径为r₂，旋转球台球内半径为r₁，旋转球台球旋转角为α。此时旋转球台的稳定平衡力计算如下。

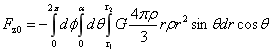
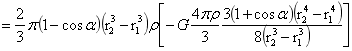…（1-35）

式（1-35）中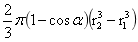为旋转球台的体积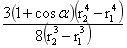，为均匀旋转球台的质心距O的距离r，r₁、r₂为旋转球体内外半径，于是有：

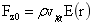…（1-36）

旋转球台的稳定平衡支撑力为：

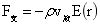…（1-37）

根据（1-36）、（1-37）以上两计算，发现稳定平衡力是球和旋转球台质量与各自质心点的引力强度的乘积，稳定平衡支撑力亦如此。

10.3 公式的极限表达

1、小球稳定平衡力和稳定平衡支撑力表达式为（1-31）和（1-32）。当图1-14如地球一样大，小球与大球比足够小，在不大的范围内，两式的引力强度在不大的范围内几乎不变，可看成定值E(或g)，于是式（1-31）和（1-32）分别有：

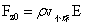…（1-38）

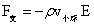…（1-39）

2、旋转球台稳定平衡力和稳定平衡支撑力表达式为（1-35）和（1-37）。当图1-14如地球一样大，小球区域换成旋转球台。旋转球台靠近外球面，旋转角α几近于零，r₁、r₂大小与地球的半径几乎相等，二者的差与球的半径比几乎忽略。在此条件下，可以证明此时的旋转球台体积与圆台的体积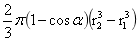几近相等或相等，其体积为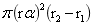，由此知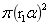为圆柱体的顶底面积S，r₂-r₁为圆柱体的高h；同样可以证明旋转球台质心到大球球心的距离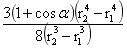几近为r=（r₁+r₂）/2，同时引力强度可看成定是值E，于是（1-35）和（1-37）分别有：

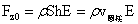…（1-40）

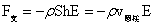…（1-41）

以上四个极限表达式，与时下浮力的表达式相同，为解开浮力的引力体系下的力学成因有重要意义。

11、总结

上面先是完成了可塑物质为球且只能为球的数理根据，进而对球的引力场强度、引力位、压力进行了计算，总结出了球内性质Ⅰ。在球内球内性质Ⅰ下提出稳定平衡力与稳定平衡支持力概念及计算公式，为下一步导出浮力等提供了理论基础。在完成可塑物质为球的过程中，张学文老师提供了极大的指导，张老师谢谢您！李相通、梁殊林、邵艳宁参与部分数理计算和支持。

参考文献

[1]宇宙观察  从地球到太阳，天体为什么都是球体，宇宙中有不规则的星球吗？  https://www.sohu.com/a/490736235_121203971  2021年09月

[2]王帅 胡森  小行星Bennu和Ryugu的新发现对小行星起源和演化的新认识（http://www.igg.cas.cn/xwzx/cutting_edge/201905/t20190505_5287635.html）  前沿报道  2019年5月

[3]傅承义 陈运泰 祁贵仲  地球物理学基础  科学出版社  1985年

[4]科学概念词条  引力场(https://baike.so.com/doc/6114669-6327810.html)

[5]谢树艺  矢量分析与场论  人民教育出版社  1978年12月

[6]李三忠等  板块驱动力：问题的本源与本质  大地构造与本质  2019年第4期（43卷）  606页

[7]巫建华 刘帅  大地构造学概论与中国大地构造学纲要[M]  地质出版社  2008年10月第一版  44页

[8]方曙 板块运动地球动力学机制研究[J]  大地测量与地球动力学  2016年9月 36（9）775-783

[9]梁光河 向中国大地构造学派致敬 科学网博客 https://blog.sciencenet.cn/blog-1074480-1442625.html  2024年7月17日

[10]王徵  奇器图说  四库全书  

[11]陈志耕 地球膨胀说提出，发展主要事实依据（J） 河北地质学院学报  1992  15（6） 586-594

[12]王竹溪  统计物理学导论[M]    人民教育出版社[M]  1978年5月

[13]范宏昌  热学[M]    科学出版社[M]  2003年2月

[14]李务伦  分子间分子作用力与质点间质点作用力是可塑物质堆砌为球的源动力  https://blog.sciencenet.cn/blog-3433895-1513214.html  2025年12月6日

[15]騰维中  再论液体表面张力的微观机理  广西物理  2000年第2期

[16]姜兆华等  应用表面化学  哈尔滨工业大学出版社  2009年  P3-6

[17]李务伦  网状周期性地球构造动力的合力场强度解释  https://blog.sciencenet.cn/blog-3433895-1282337.html  2021-4-16

[18]李务伦 李相通 梁殊林 邵艳宁  浮力形成的万有引力定律又再计算再解释  https://blog.sciencenet.cn/blog-3433895-1467553.html  2025-1-6

附录1：简单叙述中国古代关于地球研究成果

这一部分可有可无，仅是因为感叹我们先贤的伟大成就，附着于此。

明朝不晚于中晚期，前面引言部分提到已存在地球中心说，太阳中心说。地球中心说在《奇器图说》就有清晰的记载，在该书中还有引力、引力方向及引力线和压力的记载。

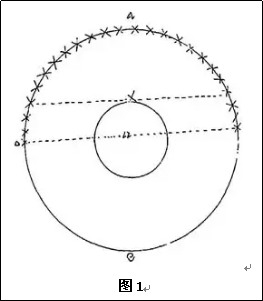
一、《奇器图说》卷一第一款原文：最重无过于地，地在天之下，必在中心。解曰：试观上图（见图1），￡￡￡￡为星天，￡为大地，￡￡为地平。人常见者，自￡至￡至￡为半天故，故知地在天之下中心也，儻使地或在￡，则其径特为少半，而星在￡￡上者不得见矣。

这一款是华夏先贤，通过天文学的长期观察，推演知道脚底下的大地，是漂浮在太空的球体。天文学助力了中华先民对所居环境的认识，是一种地球中心说。这一款解释中与现代天文学认识的太空差别较大，可以看到那个时代的科学技术的局限。但没有从理论上解释地球为什么为漂浮于太空，和地球为什么为球态两个主要问题。万有引力定律的发现，这些问题都迎刃而解。

二、《奇器图说》卷一第四款原文：重何物每体直下，必欲到地心者是。解曰：试观上图（见图2左），圆为地球，￡为地球中心，￡￡￡皆重物各体各欲直下至地心方止。葢重性就下，而地心乃其本所故耳，譬如磁石（见图2右）吸铁，铁性就石，不论石之在上在下在左在右，而铁必就之者，性然也。重物有二，一本就下，一体有斤两。

《奇器图说》卷一第十款原文：有重线过于地心，交于地平，作两直角者，为重之垂径。解曰：假如上图（见图3）图为地球中地心，横有地平线上方重，其线过地心交于地平线作两直角，故其立线为重之垂径也。

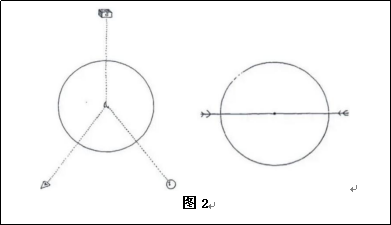
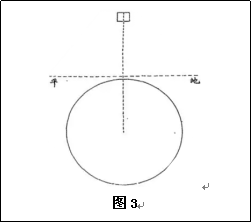
    第四款主要提立地面物体具有两的特征，一是物体受地球的吸引而有重量，一是方向。客观记录各种物体提线垂直地面，以磁铁比喻的方式推测其延长线直到地心，并受地球的吸引。而在其图示的图2左中，一、重物提线延长线经过物体的形心；二、表明物体处于稳定的静止状态。以引力场理论看，地球上任意位置提立地面的物体，1、重量是物体内部质点在引力场中受力后作用点在重心的合力，方向指向地心；2、提立地面的重物在引力场中稳定平衡；3、重物提线的延长线就是引力线；4、重物提线的延长线经物体重心，与合力的方向重合。第十款原文说了一个几何问题，但也通过图3也表现以上四点。

    图4中水柱的底面积为s，底面所受到的力为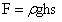。这就为该款的成立，提供了理论基础。也从种成立中，我们能体会到先贤们的洞察力和缜密科学思路。虽未提出类似式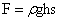的压力计算，应为后来提出这一公式打开了思路。

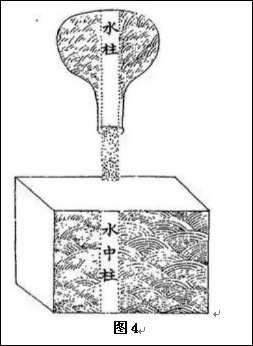
     三、《奇器图说》卷一第五十七款原文：水力压物，其重止是水柱，余在旁多水皆非压重。解曰：求水压物重处，止于所压物底之平面。求周围垂线于水上面，如水中之柱（图4）。柱乃压物之重，如上水柱图下面口底甚小，从底口垂线直至上面，中间水柱为压重，余水皆无干也。   

四、《奇器图说》卷一，有一些款项与引力场有关，下面简单叙述一下。

第五款以“本重”揭示不同物质的密度。第六款是说重体组成：点（几何形的中心）、线（应特指过形中心的线）、面（薄而重板）、形（一种面形，一种立体形）。第七款客观记述提立地面的物体稳定的状态是提线经过“心（重心概念）”，用引力场理论解释就是提立地面在引力场中所受合力作用点在重心，且合力方向在引力线上。第八款主要明确重物重心的唯一性，这唯一性用引力场理论解释就是重物在引力场中，重物内所有质点受力的合力作用在一点上，这一点就是重物的重心。其后的一些款项告诉人们如何求得不同形态的重物重心。但在第二十六款提到重物重量提立地面高度位置不同，重量不变，以引力场理论看，由于地球太大，在小的范围内引力强度变化可以忽略不计。

附录2：引力场下的积分过程

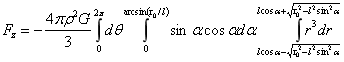
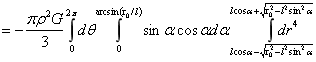
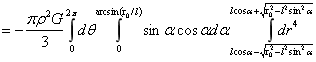
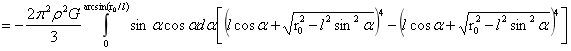
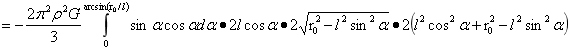
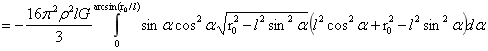
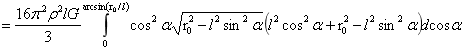…（1）

式（1）中设x=cosα，于是有：

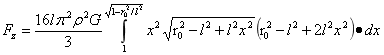
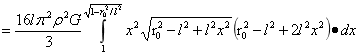
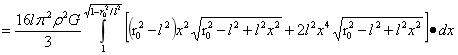…（2）

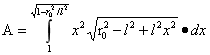式（2）中设和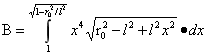

于是（2）式又可为：

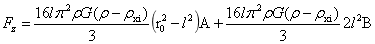…（3）

对A进行积分：

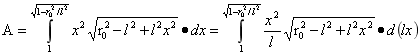
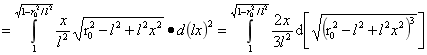
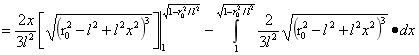
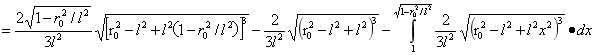
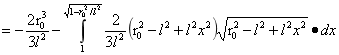
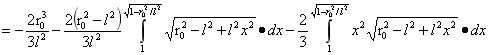
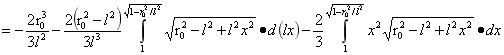
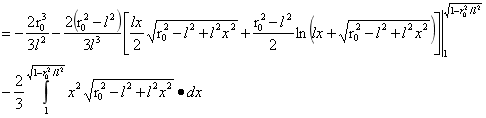
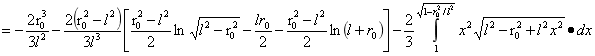
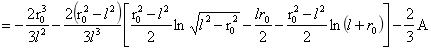…（4）

由（4）式可得A为：

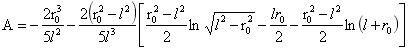…（5）

对B进行积分：

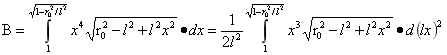
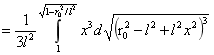
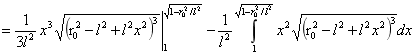
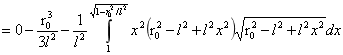
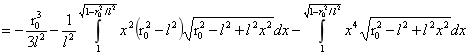
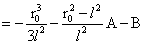…（6）

由（5）式计算可得B为：

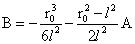…（7）

将（7）带入（3）中：

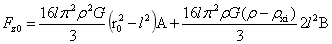
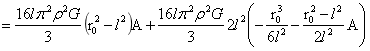
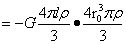…（8）