[打听，科普，资料] 莫拉维克 Moravec 的“人类能力景观图”及其更多的同类资料 （关联：“自然运算”）

莫拉维克： Hans Peter Moravec, 1948-11-30 ~

人类能力景观图： landscape of human competence

一、复习：莫拉维克曾的“人类能力景观图”

https://www.kepuchina.cn/article/articleinfo?business_type=100&classify=0&ar_id=633381

   莫拉维克悖论

   要理解机器人奔跑的意义，我们必须首先面对人工智能领域一个基本难题，即 “莫拉维克悖论”（Moravec's Paradox）。

   这是由人工智能和机器人学者所发现的一个和常识相左的现象，在 1980 年代提出，其核心是：人类所独有的高阶智慧能力只需要非常少的计算能力，例如推理，但是无意识的技能和直觉却需要极大的运算能力。

   如莫拉维克所说，要让电脑如成人般地下棋是相对容易的，但是要让电脑有如一岁小孩般的感知和行动能力却是相当困难甚至是不可能的。

   莫拉维克曾经根据自己的研究，绘制了一张“人类能力景观图”。

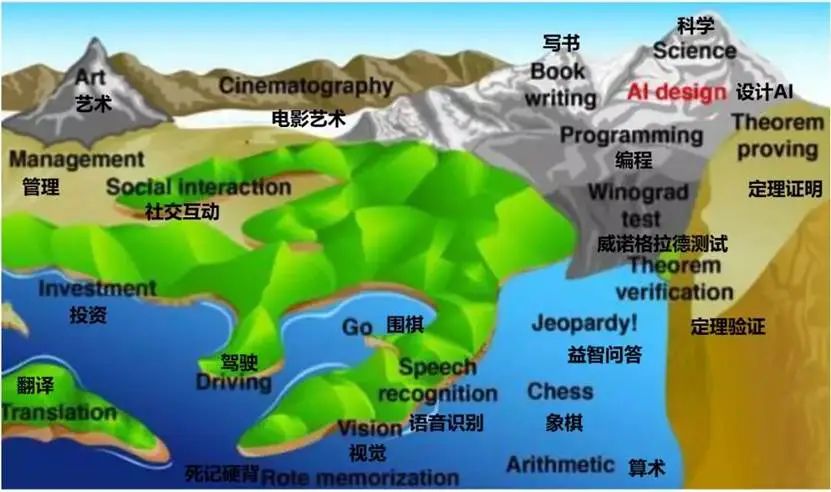
   在这张图中，被海洋所淹没的部分就是当时已经可以被人工智能和机器人所取代的工作，而随着海平面的上升，岸边、平原和高原的技能对AI来说难度逐渐上升。

   莫拉维克悖论的根源来自于生物演化的漫长历史。人类引以为傲的抽象推理能力，如逻辑和数学，从演化的时间尺度上看，是最近几千年才发展出的新能力。莫拉维克将其形容为“人类思想最薄的一层表皮” 。

   与之相反，感知和运动控制这些我们几乎不假思索就能完成的“简单”技能，是历经数亿年自然选择精心雕琢和优化的结果。大脑皮层中，有大量区域用于视觉、听觉、运动控制等感知与行动。我们低估了这些任务的复杂性，正是因为它们演化得非常高效，以至于大部分过程在我们无意识时就已完成了。

   但随着深度学习、神经网络和传感器技术的发展，某些“莫拉维克难题”已经被部分攻克，“具身智能”也逐渐在现实世界崭露头角。

https://www.kepuchina.cn/article/articleinfo?business_type=100&classify=0&ar_id=633381

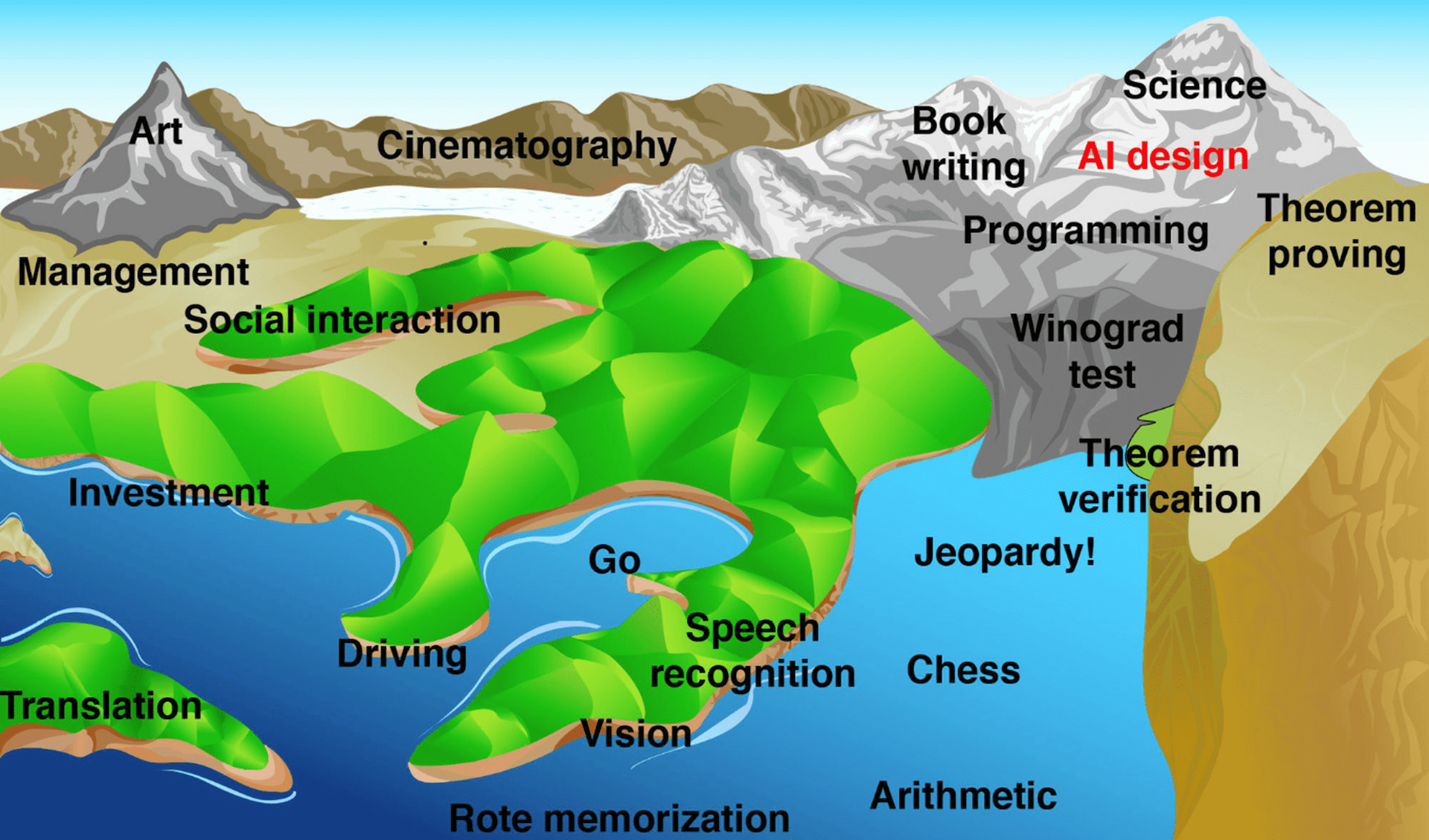
图1  AI: The Great Flood (1997-present), landscape of human competence

https://lifearchitect.ai/flood/

二、打听：关于人类能力（智能）的具体研究结果

   例如：1981年诺贝尔生理奖得主 Roger Wolcott Sperry 的“Some effects of disconnecting the cerebral hemispheres”之类的主流权威结果。

   当然，Sperry 的该结果已经初步学习了。

   现在打听的是类似的、更新的、更多的、他人的各类具体结果。

参考资料：

[1] 科普中国，2025-09-10，人工智能最想删掉的视频，再不点进来看就没机会了 

https://www.kepuchina.cn/article/articleinfo?business_type=100&classify=0&ar_id=633381

[2] Life Architect, AI: The Great Flood (1997-present)

https://lifearchitect.ai/flood/

[3] Hans Moravec. When will computer hardware match the human brain?[J]. Journal of Evolution and Technology, 1998, 1(1): 10

https://www.jetpress.org/volume1/moravec.pdf

[4] 具体思维/concrete thinking/王甦撰、姚翔，中国大百科全书，第三版网络版[ED/OL]

https://www.zgbk.com/ecph/words?SiteID=1&ID=26666&Type=bkzyb&SubID=42597

[5] 多元智力理论/theory of multiple intelligences/姚翔，中国大百科全书，第三版网络版[ED/OL]

https://www.zgbk.com/ecph/words?SiteID=1&ID=26718&Type=bkzyb&SubID=42619

[6] multiple intelligences, psychological theory, Britannica [ED/OL]

https://www.britannica.com/science/multiple-intelligences

[7] 钱学森. 关于思维科学[M]. 上海: 上海人民出版社, 1986.

https://baike.baidu.com/item/%E5%85%B3%E4%BA%8E%E6%80%9D%E7%BB%B4%E7%A7%91%E5%AD%A6/574768

[8] Roger Sperry. Some effects of disconnecting the cerebral hemispheres [J]. Science, 1982, 217(4566): 1223-1226.

doi:  10.1126/science.7112125

https://www.science.org/doi/10.1126/science.7112125

[8-2] Roger Sperry, 张尧官, 方能御. 分离大脑半球的一些结果[J]. 世界科学, 1982, (9): 1-4,64 

https://worldscience.cn/c/1982-09-28/645730.shtml

https://www.cnki.com.cn/Article/CJFDTotal-SJKE198209000.htm

[9] 杨正瓴. 逻辑能力与数理科学创新小议[J]. 科技导报, 2014, 32(1): 88-88.

http://www.kjdb.org/CN/abstract/abstract11234.shtml

[10] 杨正瓴. 人脑有多复杂？《百科知识》，1997, 7(总第216期): 39-40.

http://www.cnki.com.cn/Article/CJFDTotal-BKZS199707022.htm

[11] 杨正瓴，林孔元. 人类智能模拟的“第2类数学（智能数学）”方法的哲学研究，《哲学研究》，1999, (4): 44-50.

http://www.cnki.com.cn/Article/CJFDTOTAL-ZXYJ199904005.htm

[12] 杨正瓴. 第二类计算机构想 [J]. 中国电子科学研究院学报, 2011, 6(4): 368-374.

doi:  10.3969/j.issn.1673-5692.2011.04.009

https://mall.cnki.net/magazine/Article/KJPL201104010.htm

https://d.wanfangdata.com.cn/periodical/dzkxjspl201104009

[13] Zhengling Yang (杨正瓴). A non-canonical example to support that P is not equal to NP [J]. Transactions of Tianjin University, 2011, 17(6): 446-449.

doi:  10.1007/s12209-011-1593-5

https://link.springer.com/article/10.1007/s12209-011-1593-5

以前的《科学网》相关博文链接：

[1] 2022-08-04 14:42，[科普小资料，复习] 人脑的左右脑功能；思维的分类；多元智力理论

https://blog.sciencenet.cn/blog-107667-1349942.html

[2] 2021-11-09 14:30，[杂录] 对1999年《人类智能模拟的“第2类数学……》一文的一些扼要说明

https://blog.sciencenet.cn/blog-107667-1311664.html

[3] 2021-03-07 17:10，[备课征集] 自动化、自动控制、智能控制的未来发展方向有哪些？

https://blog.sciencenet.cn/blog-107667-1275460.html

[4] 2020-08-17 14:36，小忆“第2类数学（智能数学）”的提出

https://blog.sciencenet.cn/blog-107667-1246726.html

[5] 2018-08-31 16:47，感谢中国科学院科学智慧火花贴出《慎用“机器学习中的数据预处理：缩放和中心化”》

https://blog.sciencenet.cn/blog-107667-1132083.html

[6] 2017-10-29 19:06，随想：“人类智能”与“人工智能”

https://blog.sciencenet.cn/blog-107667-1082912.html

[7] 2024-03-23 19:58，[P vs NP，讨论，交作业] 郑波尽老师：P vs NP 的本质，及其研究方法

https://blog.sciencenet.cn/blog-107667-1426579.html

[8] 2025-4-27 22:32，[请教，往日] P对NP（二）：思考 P vs NP 的几个关键事件点

https://blog.sciencenet.cn/blog-107667-1483683.html

[9] 2024-07-04 22:46，[P vs NP，Millennium Prize，科普] William Gasarch 老师的 3 次“ P=?NP Poll ”

https://blog.sciencenet.cn/blog-107667-1440967.html

[10] 2025-05-25 06:38，[优先权？] “P对NP”已经解决。 The P vs NP (P versus NP) has been solved

https://blog.sciencenet.cn/blog-107667-1487066.html

[11] 2025-08-29 18:46，[资料，科普] 计算工具 （关联：“自然运算”）

https://blog.sciencenet.cn/blog-107667-1499619.html

[12] 2025-07-28 20:37，[资料，科普，感慨] 会使用工具的动物们 （关联：“自然运算”）

https://blog.sciencenet.cn/blog-107667-1495593.html

[13] 2025-07-27 21:40，[科普，笔记] 计算机 computer （二）早期历史 Early history （关联：“自然运算”）

https://blog.sciencenet.cn/blog-107667-1495446.html

[14] 2025-07-13 22:12，[科普，笔记] 第一台计算机 The first computer （一） （关联：“自然运算”）

https://blog.sciencenet.cn/blog-107667-1493539.html

[15] 2025-06-24 21:08，[回忆，资料，打听] “自然运算”的基础来源（铺路石）之一：帕格斯，1988，Heinz Rudolf Pagels

https://blog.sciencenet.cn/blog-107667-1491092.html

[16] 2025-06-29 22:31，[科普，笔记] 自然计算 natural computing （关联：“自然运算”）

https://blog.sciencenet.cn/blog-107667-1491690.html

[17] 2024-1-7 22:42，[搜集，小资料] 理论计算机模型的名字

https://blog.sciencenet.cn/blog-107667-1417022.html

[18] 2023-12-26 22:56，[优先权？] “自然运算”原理示意图（草图，2023-12-20 绘制）

https://blog.sciencenet.cn/blog-107667-1415467.html

感谢您的指教！

感谢您指正以上任何错误！

感谢您提供更多的相关资料！