引用本文

王鼎, 赵明明, 刘德荣, 乔俊飞, 宋世杰. 数据驱动自适应评判控制研究进展. 自动化学报, 2025, 51(6): 1170−1190 doi: 10.16383/j.aas.c240706

Wang Ding, Zhao Ming-Ming, Liu De-Rong, Qiao Jun-Fei, Song Shi-Jie. Research advances on data-driven adaptive critic control. Acta Automatica Sinica, 2025, 51(6): 1170−1190 doi: 10.16383/j.aas.c240706

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240706

关键词

自适应评判控制，自适应动态规划，数据驱动设计，在线Q学习，迭代Q学习 

摘要

最优控制与人工智能的融合发展产生了一类以执行−评判设计为主要思想的自适应动态规划(ADP)方法. 通过集成动态规划理论、强化学习机制、神经网络技术、函数优化算法, ADP在求解大规模复杂非线性系统的决策和调控问题上取得重要进展. 然而, 实际系统的未知参数和不确定扰动经常导致难以建立精确的数学模型, 对最优控制器的设计提出挑战. 近年来, 具有强大自学习和自适应能力的数据驱动ADP方法受到广泛关注, 它能够在不依赖动态模型的情况下, 仅利用系统的输入输出数据为复杂非线性系统设计出稳定、安全、可靠的最优控制器, 符合智能自动化的发展潮流. 通过对数据驱动ADP方法的算法实现、理论特性、相关应用等方面进行梳理, 着重介绍了最新的研究进展, 包括在线Q学习、值迭代Q学习、策略迭代Q学习、加速Q学习、迁移Q学习、跟踪Q学习、安全Q学习和博弈Q学习, 并涵盖数据学习范式、稳定性、收敛性以及最优性的分析. 此外, 为提高学习效率和控制性能, 设计了一些改进的评判机制和效用函数. 最后, 以污水处理过程为背景, 总结数据驱动ADP方法在实际工业系统中的应用效果和存在问题, 并展望一些未来的研究方向.

文章导读

人工智能的蓬勃发展对科技革新和产业升级带来深远影响, 推动人类社会向着数字化、现代化、智能化的方向发展. 最优控制是指找到一个最优策略, 既能够镇定被控系统或受控对象, 同时使得设定的性能指标函数最小. 最优控制问题在现实生产生活中普遍存在, 涉及系统工程、能源管理等许多领域[1]. 随着算法理论的发展和计算能力的提升, 人工智能技术在最优控制领域也得到广泛应用, 例如利用强化学习算法来优化控制策略, 赋予系统强大的自主学习和决策能力[2]. 强化学习是一种基于试错机制的智能化方法, 它强调智能体在与环境的交互过程中在线学习, 并研究其如何在环境中采取行动, 从而最大限度地增加累计奖励, 其中涉及最优化思想, 这与最优控制的核心理论不谋而合[3]. 因此, 强化学习被认为是解决复杂系统最优控制问题的重要技术之一. 

在自适应控制领域, 利用强化学习思想与最优控制理论求解复杂系统优化控制问题的方法, 通常称为自适应动态规划(Adaptive dynamic programming, ADP), 或者自适应评判设计[4]. 该方法首先基于动态规划中的最优性原理给出最优代价函数和最优控制策略形式, 然后利用强化学习中的执行−评判机制对控制策略进行反复的评价与更新, 使其逐渐逼近最优控制策略, 而神经网络通常作为算法实现过程中的函数近似工具[5]. 作为ADP方法中的三个重要组成部分, 代价函数形式一般与研究对象和实际问题相关, 评判学习机制通常对应求解方法和实现结构, 函数近似工具则关乎着目标策略的学习精度和算法复杂度. ADP最大的优势在于集成多个领域的技术, 包括人工智能领域的强化学习算法和神经网络技术、控制领域的最优反馈与自适应调控技术、数学领域的迭代算法、计算智能领域的优化算法等. 一方面, 不同领域新技术的涌现可以促进ADP的进一步发展, 提升复杂系统的控制性能. 另一方面, ADP也有助于改进已有的技术, 例如使用ADP代替传统的梯度下降算法来训练神经网络[6]. 总之, 在智能技术的日新月异发展下, 具有强大自学习和自适应能力的ADP更符合自动化系统设计的潮流, 在多智能体系统[8]、能源系统[9]、化工系统[10]、生物系统[11]上具有广泛的应用前景. 

纵观ADP方法的发展历程, 可以按照不同的标准进行分类. 考虑有无系统模型可分为基于模型的ADP方法和数据驱动的ADP方法, 考虑策略评估方式可分为值迭代ADP方法和策略迭代ADP方法, 考虑算法执行方式可分为在线学习ADP方法和离线学习ADP方法. 近年来的综述文献和学术专著, 对于基于模型的ADP方法, 在迭代算法的收敛性、控制策略的稳定性、方法实现的高效性等层面已进行详细总结[12−17]. 针对离散非线性系统的最优控制问题, Al-Tamimi等[18]在2008年提出一种初始条件为零的值迭代算法, 并证明了代价函数序列以单调非减的形式收敛到最优值. 这是第一次从数学上证明了零初始化值迭代算法的收敛性, 极大地推动迭代ADP算法的发展. 随后的十几年中, 学者们在初始化函数设计和值迭代更新过程方面做出大量的工作, 提出广义值迭代[19−22]、稳定值迭代[23]、局部值迭代[24]、演化值迭代[25]、集成值迭代[26]、多步值迭代[27−28]、$ \lambda $步值迭代[29−31]、并行值迭代[32]、平行值迭代[33]、可调节值迭代[34−35]、进化值迭代[36]等一系列算法, 有效地减少了传统值迭代算法的计算量和保证了迭代过程中控制策略的稳定性. 与值迭代算法不同, 策略迭代算法要求一个容许策略进行初始化. 2014年, Liu等[37]首次分析离散时间策略迭代算法的学习过程和相关特性, 证明了代价函数序列以单调非增的形式收敛到最优值, 这意味着迭代过程中的控制策略都是容许的. 在此基础上, 又衍生出性能更优的广义策略迭代[38]、局部策略迭代[39]、平衡策略迭代[40]、多步策略迭代[41]、$ \lambda $-策略迭代[42]、加速策略迭代[43]等算法. 值得一提的是, 这些基于模型的迭代ADP算法一般是离线实现的, 即通过离线迭代获得最优控制律后, 再将其作用于被控系统. 与之相对应的是基于模型的在线ADP算法, 它不再需要离线迭代, 而是直接采取在线自适应的方式获得最优控制律[44]. 目前, 基于模型的在线ADP算法在最优调节[45−46]、零和博弈[47]、跟踪控制[48−50]、事件触发控制[51−52]、鲁棒控制[53−54]、容错控制[55]、分散控制[56]等方面已有比较丰富的研究成果. 

上述ADP算法大多是基于模型的方法, 在过去的二十年中一直是该领域的研究热点. 然而, 在工程实际中, 未知的系统结构或参数经常给最优控制器的设计带来挑战. 为解决模型未知情况下的优化控制问题, 无模型或数据驱动的ADP方法受到广泛关注[57−61]. 实际系统在运行过程中会产生大量的过程数据, 这些离线和在线数据在一定程度上能够反映出系统的内在特性和运行规律. 在这些数据的赋能下, 数据驱动的ADP方法同样能够为复杂系统设计出稳定、安全、可靠的控制器. 数据驱动的ADP算法可分为两类, 即间接数据驱动的ADP算法和直接数据驱动的ADP算法. 间接数据驱动的ADP算法是指先利用数据建立近似的系统模型, 然后再进行控制器的设计和性能分析[62−64]. 相比之下, 直接数据驱动的ADP算法是指直接利用数据进行控制器的设计, 省去系统模型建立的过程[65−68]. 从本质上来说, 间接数据驱动的ADP算法的控制器设计利用近似系统模型, 所以相应的实现技术和理论特性与基于模型的ADP方法大致一样. 然而, 直接数据驱动的ADP算法则具有完全不同的实现结构, 理论特性也不能简单地移植. 因此, 本文将重点关注直接数据驱动的ADP算法. 事实上, 我们无意比较“基于模型的ADP算法”和“数据驱动的ADP算法”的性能优劣, 因为这两类算法在不同场景下具有各自的优势. 但对于系统模型难以建立且环境实时变化的情况, 数据驱动的ADP方法则展现出更广泛的应用前景和更大的发展潜力. 

1989年, Werbos提出执行依赖启发式动态规划(Action dependent heuristic dynamic programming, ADHDP)结构[69]. 在ADHDP结构中, 评判网络的输入不仅有系统状态, 还有控制输入, 这意味着评判网络已经包含系统模型和效用函数的信息, 可直接通过最小化评判网络的输出得到控制律[70]. 因此, ADHDP是一种数据驱动的ADP方法. 实际上, ADHDP与Watkins博士论文中提出的Q学习算法在本质上为同一种结构, 因此ADHDP也称为Q学习[71]. Q学习算法最初的研究主要集中在线性系统的最优控制理论和应用. 2007年, Al-Tamimi等[72]提出一种基于值迭代的在线Q学习算法, 用于解决离散时间线性系统的零和博弈问题. 2014年, Kiumarsi等[73]提出一种策略迭代Q学习方法, 在线实现了离散时间线性系统的数据驱动跟踪控制. 这两种Q学习算法为应用ADP方法解决线性零和博弈问题和跟踪控制问题设计了基本框架. 值得一提的是, 为确保对状态空间的充分探索, 通常需要加入探测噪声用于满足持续激励条件. 然而, 针对Bellman方程, 探测噪声可能会导致求解不准确. 为避免引入探测噪声带来的偏差, Jiang等[74]在2012年提出一种在线求解连续时间线性系统最优控制律的策略迭代算法, 核心是引入辅助变量对原系统进行重新描述, 这使得具有探测噪声的控制输入不会影响学习过程的收敛性和最优性. 在此基础上, 2017年Kiumarsi等[75]明确提出基于off-policy形式的强化学习算法, 有效实现了离散时间线性系统的在线$ H_{\infty} $控制. 2022年, Farjadnasab等[76]提出一种融合off-policy学习的无模型方法用于设计线性二次型调节器, 其过程主要是基于具有线性矩阵不等式约束的非迭代半定规划, 该方法的优势包括三个方面, 即提升采样效率, 对模型不确定性具有鲁棒性, 并且不需要初始稳定控制器. 2023年, Lopez等[77]构建一种基于高效off-policy形式的Q学习算法, 与基于线性矩阵不等式解的控制设计方法相比, 其主要优点是降低了计算复杂度, 不需要初始稳定控制器, 并且对测量数据中的小干扰具有鲁棒性. 简单来说, 若产生数据的控制策略与目标策略不是同一个, 这样的学习形式称为off-policy学习. 反之, 若产生数据的控制策略与目标策略是同一个, 则称为on-policy学习. 目前, 普遍认为off-policy学习具有更好的探索能力. 近十年来, 许多面向线性系统的Q学习算法都以off-policy学习形式实现[78−83]. 随着线性系统数据学习范式的完善, 学者们将研究重点转向迭代算法的性能改进. 2023年, Qasem等[84]提出混合迭代Q学习算法, 核心是利用值迭代提供初始容许策略, 然后使用策略迭代获得连续时间线性系统的最优控制策略. 2024年, Jiang等[85]提出改进的$ \lambda $-策略迭代算法, 能够减少算法的迭代次数, 并给出严谨的收敛性分析. 2024年, Zhao等[86]提出一种面向连续时间线性系统的单环策略迭代算法, 能够以更少的时间获得博弈代数Riccati方程的解. 如今, 面向线性系统的Q学习方法已经与控制理论和应用深度融合, 研究对象涉及博弈系统[87]、时滞系统[88−89]、随机系统[90]、执行器故障系统[91]、大规模系统[92]、网络化系统[93]、多智能体系统[94−96]等, 应用层面包括机器人移动[97]、互联车辆控制[98]、微电网控制[99]、同步发电机控制[100]等. 总的来说, 线性系统Q学习算法在收敛性、稳定性、鲁棒性、数据驱动范式、评判学习机制、实际应用等方面已具有相对成熟的工作. 

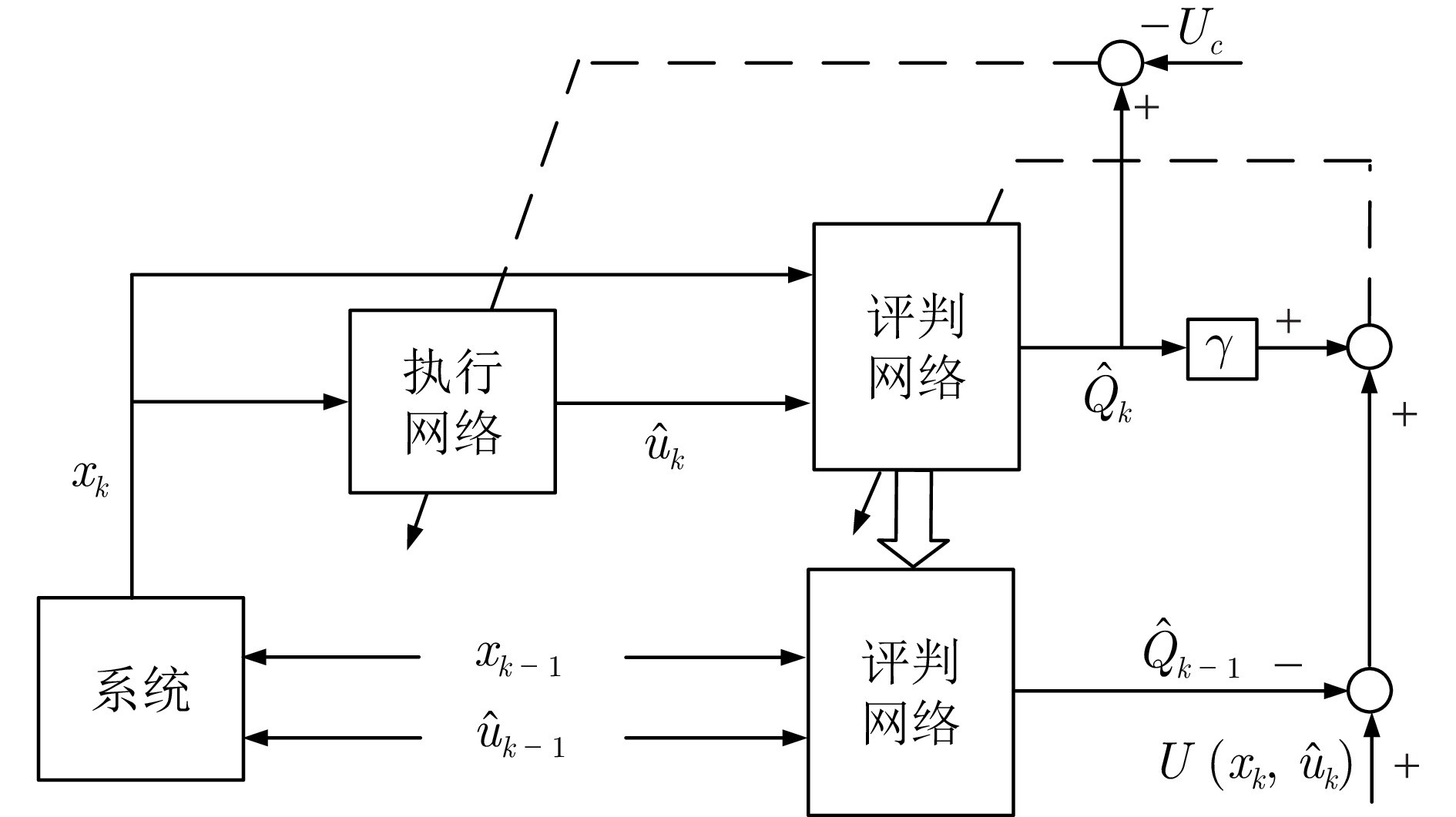
在各行各业的控制应用中, 非线性系统普遍存在. 为实现最优控制, 一个传统的做法是将非线性系统简化或者近似为线性系统, 之后再利用已有的线性系统理论完成控制器的设计. 然而, 随着工业系统规模的扩大, 控制对象的复杂性不断增加, 并展现出强烈的非线性和未知性. 在这种情况下, 为模型未知的复杂非线性系统设计最优控制器, 对于确保系统正常运行并达到预定的性能指标具有重要意义. 早在2001年, Si等[101]就提出在线Q学习算法, 将当前时刻的代价函数和效用函数相加, 与上一时刻的代价函数作差, 通过最小化误差来实时更新评判网络权值. 然后, 根据最小化代价的原则调整执行网络的权值, 并将执行网络作为神经网络控制器, 实现对非线性系统的在线控制. 这种做法也常称为在线强化学习、在线ADHDP或者direct HDP方法. 2012年, Liu等[102]以三层反向传播神经网络作为评判网络和执行网络的实现工具, 在假设输入层到隐藏层权值不变的前提下证明了在线Q学习算法的一致最终有界性. 2015年, Sokolov等[103]进一步给出输入层到隐藏层和隐藏层到输出层权值同时更新情况下的一致最终有界性. 这些工作都是基于目标策略产生的数据进行在线学习, 属于on-policy学习方法, 无法充分利用数据且需要较长的学习周期. 为提升学习效率, Malla等[104]将经验回放技术集成到传统的ADHDP方法中, 提高了算法学习的成功率和减少了训练时间. 从原理上讲, 能够利用过去的数据也属于off-policy学习方法. 总之, 上述在线Q学习算法重点研究控制器与系统实时交互场景下的系统稳定性和代价最优性. 

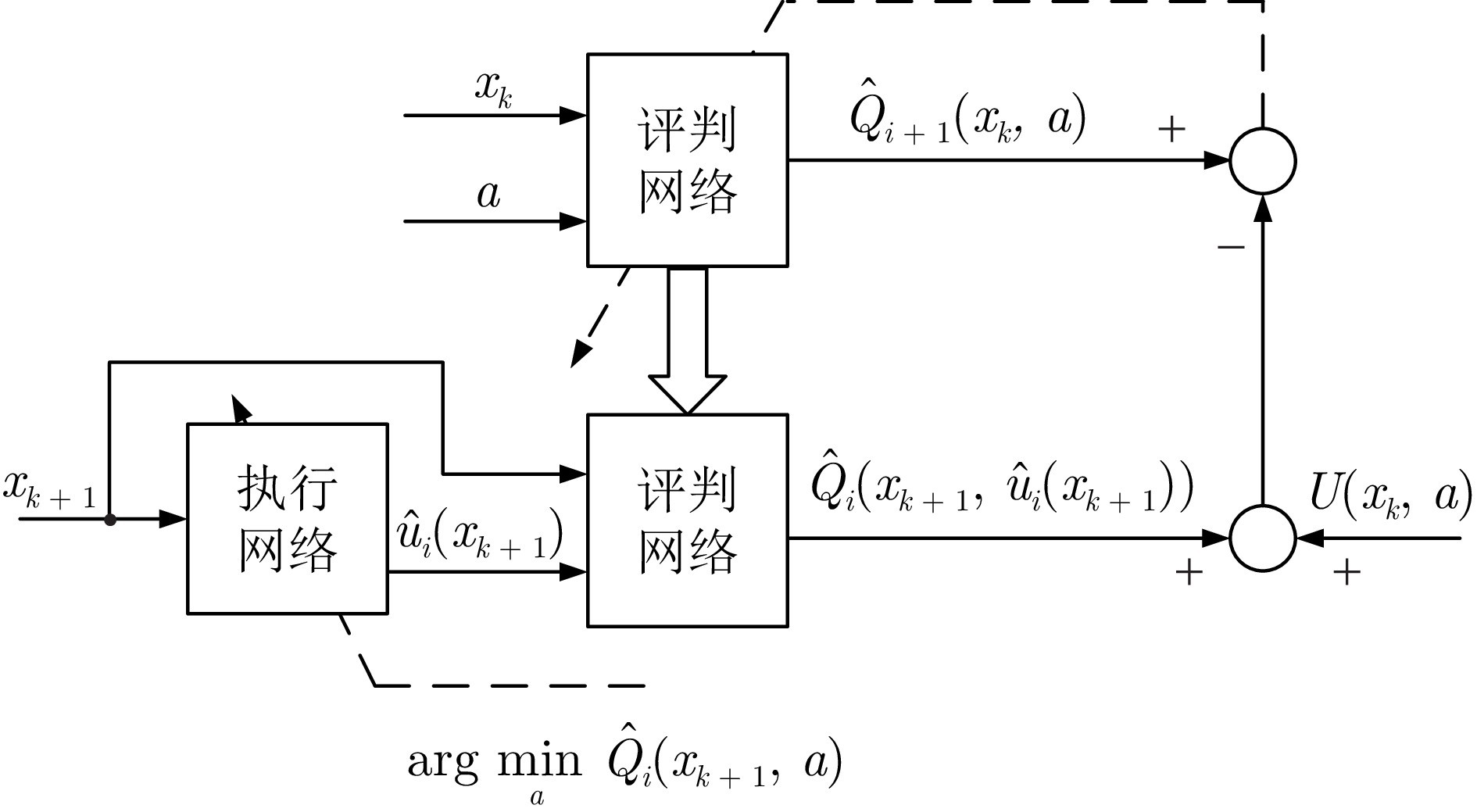
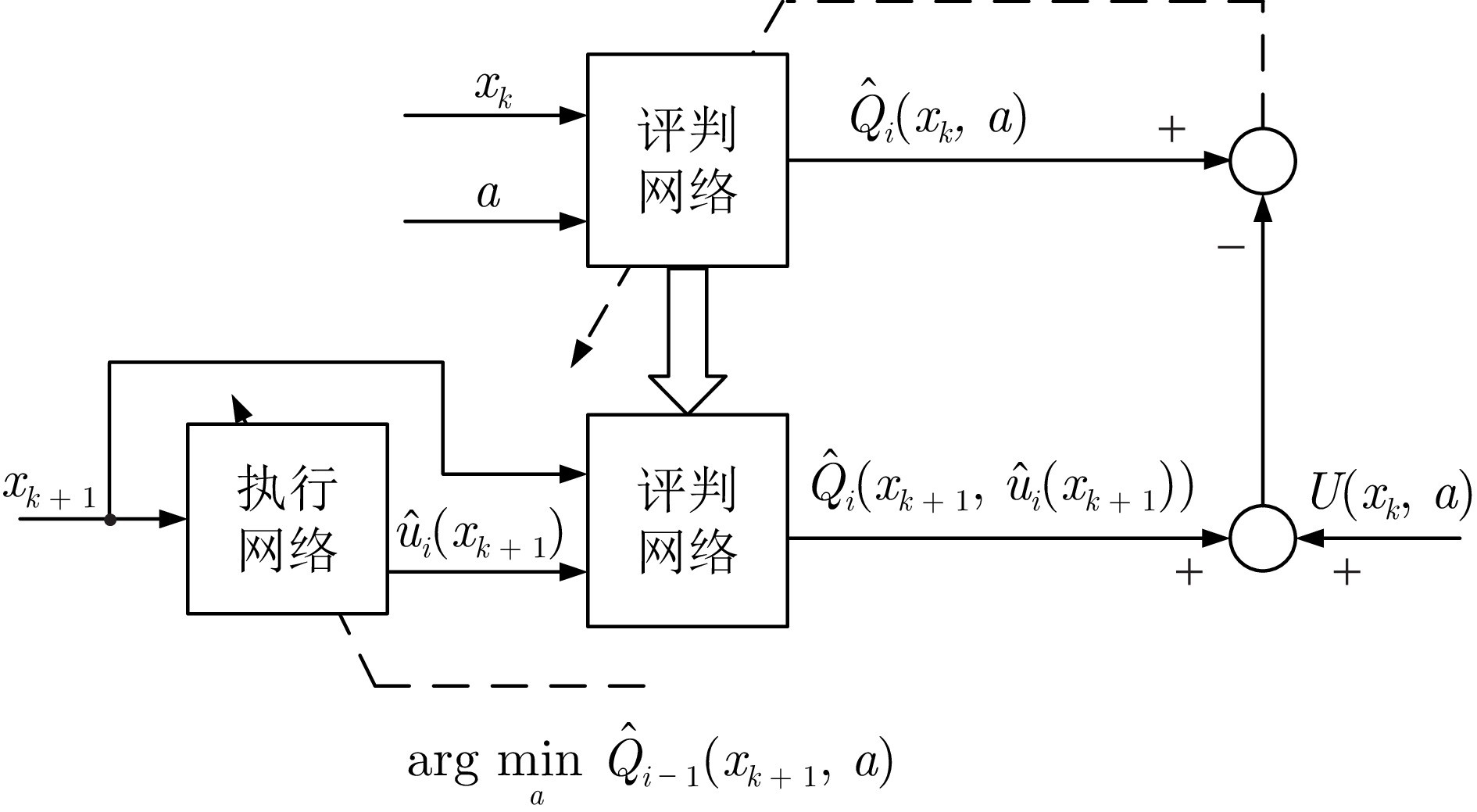
近十年来, 关于非线性系统的迭代Q学习算法也涌现出大量的研究成果. 2014年, Luo等[105]提出无模型的近似策略迭代算法, 通过提前收集连续时间系统的真实数据, 以迭代学习的方式获得近似最优控制律. 针对模型未知离散时间非线性系统的最优控制问题, Zhao等[106]在2015年提出一种需要初始容许控制的策略迭代Q学习算法, 并详细给出收敛性和稳定性分析, 重点指出每一个迭代策略都是容许的. 2024年, Xu等[107]提出一种基于并行交叉熵优化方法的策略迭代Q学习算法, 通过求解二次规划问题获得初始容许的跟踪控制策略, 并证明了Q函数序列以单调非增的形式收敛到最优值. 2017年, Wei等[108]提出确定的值迭代Q学习算法并严格证明了其收敛性. 2024年, 王鼎等[109]运用值迭代Q学习算法解决了离散时间随机系统的最优控制问题. 此后, Qiao等[110]建立基于加速值迭代的Q学习框架, 面对大量数据时能够以较小的计算代价获得最优Q函数. 这些方法都是利用提前采集的状态和控制数据对迭代Q函数进行更新, 从而获得目标迭代策略, 属于off-policy学习方法. 至今, 学者们对迭代Q学习算法的收敛性、稳定性、数据学习范式做了大量研究, 并给出不同应用场景下的算法实现结构. 然而, 目前尚没有文献对此进行归纳和凝练. 此外, 在开展实际的数据驱动控制过程中, 安全性、高效性、实用性也是需要考虑的重要特性. 安全性是指在不损伤系统的情况下, 仅利用历史数据获得最优控制策略. 高效性是指在面对大量数据时, 利用已有的知识或信息减少计算成本. 实用性是针对复杂工业系统, 降低控制器设计的复杂度. 针对未知环境下的一类最优控制问题, 本文将从经典的在线和迭代Q学习算法引入主题, 着重分析算法的理论特性和实际应用. 然后, 以实现高效学习和提升性能为目标, 提出一些新颖的Q学习算法. 最后, 展示一些典型应用场景并给出总结. 

图 1  在线Q学习算法结构图

图 2  确定的值迭代Q学习算法结构图

图 3  确定的策略迭代Q学习算法结构图

本文总结了数据驱动自适应评判方法的基本原理和研究现状, 并提出一系列先进的评判学习机制和函数设计形式. 首先, 从非线性系统的最优调节问题入手, 阐述在线Q学习算法和迭代Q学习算法的实现结构、理论特性以及数据学习形式; 其次, 为实现高效学习, 回顾了已有的加速Q学习和迁移Q学习算法, 并设计了改进的加速和迁移学习机制; 再次, 阐述Q学习算法在解决跟踪、安全、博弈等问题上的研究成果, 并构建了改进的效用函数形式; 最后, 分析了数据驱动自适应评判方法在污水处理过程中的应用和挑战, 重点指出进一步开展增量、安全、鲁棒Q学习算法研究具有实际意义. 随着数据驱动自适应评判控制的理论研究日渐深入, 利用强化学习、迁移学习、深度学习等人工智能技术创新作为突破口, 积极推动自动化与智能系统产业技术发展, 具有重要的应用前景. 

作者简介

王鼎

北京工业大学信息科学技术学院教授. 主要研究方向为强化学习与智能控制. 本文通信作者. E-mail: dingwang@bjut.edu.cn

赵明明

北京工业大学信息科学技术学院博士研究生. 主要研究方向为强化学习和智能控制. E-mail: zhaomm@emails.bjut.edu.cn

刘德荣

南方科技大学自动化与智能制造学院教授. 主要研究方向为强化学习和智能控制. E-mail: liudr@sustech.edu.cn

乔俊飞

北京工业大学信息科学技术学院教授. 主要研究方向为污水处理过程智能控制和神经网络结构设计与优化. E-mail: adqiao@bjut.edu.cn

宋世杰

西南交通大学智慧城市与交通学院讲师. 主要研究方向为强化学习和智能控制. E-mail: shijie.song@swjtu.edu.cn