一、文章亮点介绍

1. 本文提出在传统的持续再评估方法 (Continuous Reassessment Method, CRM) 的基础上，利用mTPI （modified Toxicity Probability Interval） 设计、BOIN (Bayesian Optimal Interval) 设计、Keyboard设计以及i3+3设计的剂量分配规则进行决策。这种方式有效结合两类设计方法的优势，提高了模型在准确性和安全性上的试验表现。

2. 将传统持续再评估方法寻找最大耐受剂量 (Maximum Tolerated Dose, MTD) 改为寻找可接受的最大毒性耐受区间，使得在选择目标毒性时具有更大的灵活性。

3. 本文利用模拟分析，通过对MTD选取比例、病人剂量分配百分比、平均中毒人数以及药物过量率四个维度对提出模型和传统模型进行了比较，证明了提出的设计具有更好的表现，且提出了各自更为适合的实验情景。

二、文章介绍

1. 研究背景及目的

在临床一期剂量探寻的试验设计中，持续再评估方法可以通过数据的不断累积和收集，达到更准确地找到人体可接受的最大耐受剂量。然而该方法仍因过于激进的剂量爬坡决策而受到批评。此外，传统的持续再评估方法仅针对目标中毒概率进行点估计，使得其在目标设置上缺乏灵活性。模型辅助类实验设计 (Model-assisted Design) 在实践中通常具有更高的安全性，确保更少的人出现剂量限制性毒性 (Dose Limiting Toxicities, DLT)。但是由于该类模型设计中仅依据某一当前剂量下的历史数据进行决策，而没有考虑其他剂量下受试病人的信息，导致对MTD选取的准确性较持续再评估方法普遍较差。因此，如何能够在保持准确性的情况下，尽可能地提高试验的安全性，是临床一期统计试验设计的研究的核心之一。

本文结合两种设计的优势，通过将mTPI (modified Toxicity Probability Interval) 设计、BOIN (Bayesian Optimal Interval) 设计、Keyboard设计以及i3+3设计的剂量分配规则应用在持续再评估方法中进行决策，并引入了可接受的最大毒性耐受区间为目标，提出了四种新的实验设计。

2. 模型及结果分析

本文以持续再评估方法的概率模型为基础，采用mTPI (modified Toxicity Probability Interval) 设计、BOIN (Bayesian Optimal Interval) 设计、Keyboard设计以及i3+3设计的剂量分配规则进行剂量爬坡决策，提出了四种全新的实验模型。

iCRM

定义每个剂量水平的后验概率落在最大毒性耐受区间 (0.25, 0.35) 内的概率为T_i为如下：

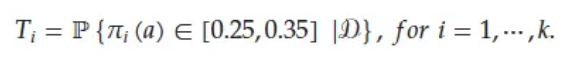
下一组推荐的剂量水平J将根据以下方案进行决策：

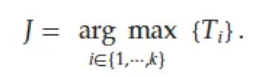
• mCRM

设定ε₁=ε₂=0.05。根据患者的反应，如果某一剂量的中毒概率落在(0, φ_T - ε₁), [φ_T - ε₁, φ_T + ε₂], (φT + ε2, 1] 概率区间的后验概率质量最大，则分别应增加、保持或减少下一组受试病人的剂量。即

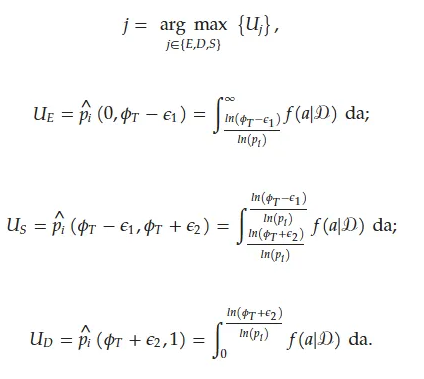
• bCRM

在这个模型中，计算剂量水平i的平均后验毒性概率，并根据以下规则为下一个患者选择剂量：

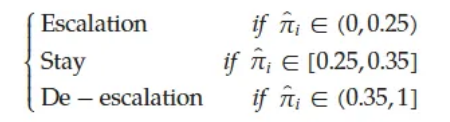
• kCRM

首先选择目标毒性概率区间为(0.25, 0.35)，当区间宽度为0.1时，划分出其他间隔为 (0.05，0.15)、(0.15，0.25)、(0.35，0.45)、(0.45，0.55)、(0.55，0.65)、(0.65，0.75)、(0.75，0.85) 和 (0.85，0.95)。定义键Mj表达如下：

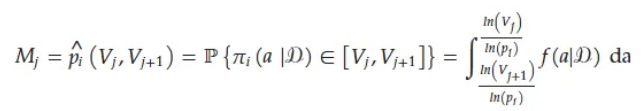
最强键K为具有最高后验概率质量的键，即：

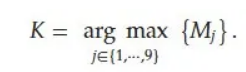
根据K的位置，剂量升降可总结为：

模拟结果表明，本文提出的设计在绝大多数情景下达成了最优表现，即拥有较高的正确找到MTD的概率的同时，实现了相对有效的过毒控制。部分结果见图1和图2。

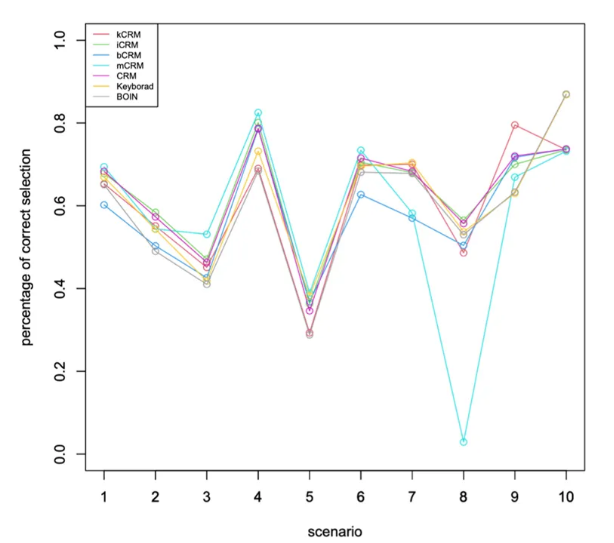
图1. 各情景下模型正确选择MTD的比例

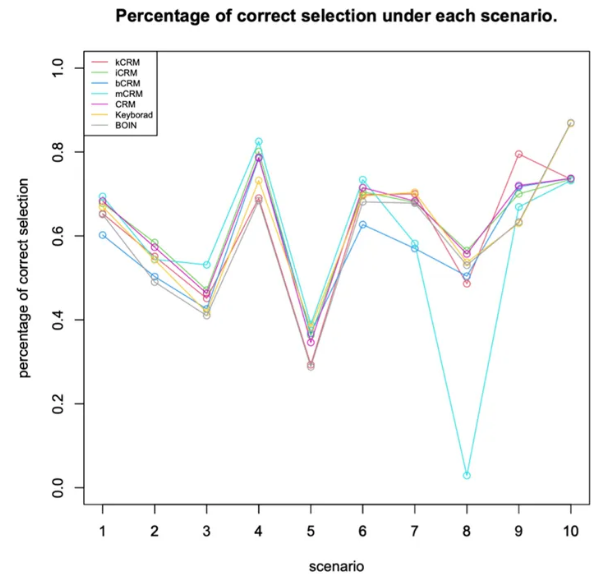
图2. 各情景下平均中毒人数

3. 讨论与总结

在本文中，我们提出了四个新的基于持续再评估方法的实验设计。将模型辅助类实验设计中的剂量分配规则和持续再评估方法的模型框架相结合，使得新的模型能够较为准确地估测MTD的同时，保证了安全性，有效控制了受试者被分配到过毒剂量的概率。通过数值模拟的方式，证明了四个设计均能达到改善应用表现的目的。敏感性分析有效地检验了新设计在不同真实情景下仍能保持稳定的表现。作为实验设计改进，作者们提供了一种结合模型优势的新思路。同时为今后的工作提供了借鉴，作者将探索此种改进思路在其他与临床一期相关的实验设计方向上的可行性。

三、作者介绍

姓名：肖嘉诚

机构：西交利物浦大学金融与精算数学系

研究方向：生物统计

姓名：张维佳

机构：西交利物浦大学金融与精算数学系

研究方向：生物统计；亚组分析；健康经济

姓名：李融

机构：西交利物浦大学金融与精算数学系

研究方向：金融风险管理；精算控制论；生物医学统计方法

姓名：温从华

机构：西交利物浦大学金融与精算数学系

研究方向：应用概率及量化金融

学术成果：作为主持人和重要参与者完成10多项国家及省部级科研项目，累计基金达500多万，在国际一流杂志发表35余篇文章。学术成果发表于Finance Research Letters, British Accounting Review, European Journal of Finance, International Review of Financial Analysis, Pacific-basin finance journal, Journal of computational and applied mathematics 等一流量化金融和计算数学杂志中。

学术兼职：目前担任中国统计教学学会理事会理事，中国现场统计研究会大数据统计分会理事，并在多个省市科研学会中兼任理事或高级顾问。

原文出自Mathematics 期刊：https://www.mdpi.com/3211792

期刊主页：https://www.mdpi.com/journal/mathematics

Mathematics 期刊介绍

主编：Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK

期刊主题涵盖纯数学和应用数学所有领域，重点发表代数与逻辑、几何与拓扑、数学分析、统计与运筹学、应用数学，包括数学与计算机科学、控制理论与力学、数学生物学、数学物理、金融数学等数学在其他各学科应用的文章。现已被SCIE (Web of Science)、Scopus等重要数据库收录，JCR category rank: 21/489 (Q1)。

2023 Impact Factor：2.3

2023 CiteScore：4.0 

Time to First Decision：18.3 Days

Acceptance to Publication：1.9 Days