管克英

北京交通大学理学院，数学系

Email：keying.guan@gmail.com

摘要：指出光滑的空间闭曲线除了扭结结构外，还存在另一个重要的微分拓扑不变量，即围绕某个轴的旋转（圈）数, 而且只有将数学与物理两方面相结合才能准确描述旋转圈数这一概念。

一. 物理背景和数学问题

笔者2016年曾在科学网发布了博文 

• 莫比乌斯带、扭结与空间极限环的倍周期分叉--研究进展 （已有12527 次阅读）热度 2 2015-4-24 17

之后，2018年笔者进一步在科学网提出了空间闭曲线旋转（圈）数的概念，

空间Frenet闭曲线的微分拓扑不变量--旋转数

由于当时笔者的电脑硬盘损毁，相关的详细论文无法找回，又因同时关注其它问题，而且经历了长时间的疫情期变得懈怠，这方面的研究被搁置。直到最近，注意到该项研究与我近些年关于“静力也做功”和“功率与力的等价性”的物理研究直接相关，所以更细致地总结了一下自己的研究结果撰写了现在的这篇博文。

为使读者直观地理解此问题的物理与数学背景，笔者附上几张生活中常见的照片:

图一. 冲牙器

图一是一个使用多年的电动冲牙器。关注牙刷把柄下方链接着一个盘了6圈的PVC水管，水管的另一端固定连接到储水箱。相信，水管被盘了6圈的结构在出厂前已经过预处理呈稳定状态。在使用时，人们一般是手握住牙刷把柄拉长通水管，使牙刷对准使用者的牙齿。在拉长的过程中，水管像个被拉长的弹簧（螺线），握住手柄的手部会感到水管要恢复到原盘转位置的越来越大的弹性恢复力。

图二.  被拉开的水管

由于冲牙器的位置离使用者的牙齿距离不大，使用时，六个圈形结构虽然变形但仍会保留（如图二），人们不需要，也不会迅猛地将水管拉成无圈形结构的笔直管道。常识表明，如果这样地瞬间拉直水管，水管材料就会受损或断裂。

再研究另一类似的实例：

图三.  盘起的充电线揽

图三显示的是笔者的电动汽车在家充电时使用的充电线缆。缆线的一端是个 (连接到车上充电插口的) 插头，它是个带有车辆插头锁和释放按钮的近圆柱体。另一端是个长方形的电线状态指示器, 指示器再连着一个120 伏插头。为方便，平时该电缆盘成8圈而且被绑带束缚，放置在车的后备箱下层。由于长时间这样放置，电缆线已适应了这种8圈的盘型结构，即使松开绑带也不会自动恢复成直线的形状。在家充电时，笔者需要解开固定的束缚绑带，先将圆筒形的插头插入车上的充电口，然后握住另一端的长方形指示器拉长充电线缆，将电源插头插入电源。此时，类似于上例中拉长PVC水管一样，在拉开电缆线的过程中，电缆仍保留原有的8圈结构（见图四），而且电缆线对两端的插头部分形成越来越强的弹性恢复力。

图四.  被拉开的电缆线。

好在院子中的电源离电动车不远，不需要将电缆强行拉直。常识告诉我，若急速强行拉直电缆线必然使此电缆系统遭受结构性的损害。

生活中，这样的例子举不胜举。

这类例子均涉及到给定长度并具有一定弹性与塑性材料（如塑料、碳纤维、橡胶、钢铁或植物纤维等）制成的长“线” ，或 长“细管”。假定使用前，该“线”（或长“细管”）围绕某个较粗的（可以是虚拟的）轴，盘成 n (整数）个圈的螺线形,  在使用时将螺线的一端固定，把持住螺线的另一端（即禁止螺线在该端点处发生扭转）将螺线拉开、拉长，在此过程中，螺线的形状会变化，但其 n 个圈的结构将会被保持，不会被瞬间拉成直线。除非曲线材料的内在结构发生质变，材料的弹性完全消失成为纯塑性材料、或发生断裂，n 个圈的拓扑结构才会变化。这无疑关系到深刻的物理、化学机制。

因此，从物理意义上，将上述线材的旋转圈数 n 作为拓扑不变量是有意义的。

在数学上，这类例子则涉及到微分几何中的空间曲线不变量问题。

首先要说明的是，为什么用物质材料制作的细长线或长管可以用空间曲线表示？

虽然空间曲线是空间中没有粗细的一维光滑曲线，但在微分几何可描述的范围内，一般要求描述曲线各点位置矢量依赖的一维参数 t 的表达式必须存在对该参数的连续三阶导数。在此基础上，就可沿曲线各点建立三维的，以单位切（线）向量 T、单位主法（线）向量 N 和单位副法（线）向量 B 张成的坐标架(亦称 Frenet 坐标架）（图五）。

图五. 空间曲线的切向量 T，法向量 N 和副法向量 B。

照片载自英语维基百科的Salix alba

Illustration of the frenet frame. Created using Singsurf.org and Javaview.de postprocessed with gimp.

关于向量 T、N 和 B 的严格定义与数学表达式将在本文的第二节介绍，读者也可在任何微分几何的教科书中找到。

随着参数的连续变化，附着在曲线点的坐标架也在一起移动并围绕着切矢量转动。由于是空间曲线，这个转动一定几乎处处存在。因此可以想象，整个空间曲线外包着一个半径为单位长度的（无厚度）薄管，使得当坐标架随曲线上的点连续变动时，单位主法向量与副法向量的末端箭头分别在那个薄管壁上留下各自的轨迹。由于一般假设所研究的空间曲线不存在交叉点，可以认为，上述想象的那个包在曲线外的薄管也不相互接触，这是因为，长度单位可以任意地选择适当的小，以便避开薄管交叉的可能。因此，用数学上的空间曲线连同那个想象中的薄管合在一起即可代表用实际物质材料制成的有固定粗细的细长线或长管。

数学上，上述例子的 n 圈曲线，在微分拓扑同伦意义上等价于一段 n 圈圆柱螺线。图六显示了一个盘旋10圈的圆柱螺线：

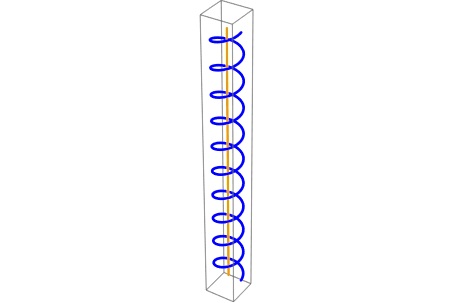
图六.  有10个圈的圆柱螺线段

曲线段的旋转圈数 n 属于该曲线的内在大范围（亦称整体）性质。为更圆满地研究拓扑流形的整体的性质，拓扑学一般使用闭流形。闭流形是没有边界的紧流形 （参考维基百科 https://en.wikipedia.org/wiki/Closed_manifold）。这是因为在边界处微分计算时存在一些需要特殊处理的问题，例如必须使用单侧导数的概念。上述的圆柱螺线段不是一维的闭流形（因为它有两个不是一维开集的边界端点），所以不太理想。

恰好由于该螺线段的两个端点处的单位切向量，单位主法向量和单位副法向量的方向分别对应相同，所以可以想象，通过拓扑变换将螺线的两端看作同一个点（如图七），使之成为有  n 个圈的没有边界的空间闭曲线（一维闭流形）。

图七.  有10个圈的空间闭曲线

为说明以上（微分）拓扑做法的合理性，研究以下二维闭流形研究中的一个著名例子，克莱因瓶（图八）的构造方法。

图八.  克莱因瓶 （载自维基百科，图作者 Tttrung ）

按照维基百科关于词条 “克莱因瓶”的解释：先试想一个底部镂空的红酒瓶, 它在数学上被想象想为有两个圈形一维边界的二维定向曲面，其中一个边界是瓶口，另一个是刨去瓶底的剩余瓶面的底线，然后延长其颈部，向外扭曲后伸进瓶子的内部，再使瓶口与底部边界相连接，这样便将克莱因瓶虚拟地构造出来。

比较，上述的由 n 圈圆柱螺线段构造 n 圈闭曲线的方法，与克莱因瓶的构造方法，不难看出前者在三维空间内是可实现的，后者则在三维空间内不能实现。因此前者的构造方法显得更真实、更合理。

直观上，上述空间闭曲线的旋转（圈）数 n 应该是一种微分拓扑不变量。如果取消“微分”一词，仅从拓扑学角度，图七显示的空间闭曲线是可连续变换（或同伦变换）成平面圆周，此情况下旋转圈数是不能当作拓扑不变量的，所以从数学上定义这个不变量则不那么简单。

可以发现只有将曲线的数学性质与物理内涵适当结合，或者从微分拓扑角度，将空间曲线相关的结构“物质化”才能给出合理的定义方式。这部分内容将在博文的第二节介绍。

（待续）