By Keying Guan with ChatGPT

Correspondence: keying.guan@gmail.com

Abstract

We study the asymptotic behavior of a newly proposed ratio involving the cumulative sum of the first n prime numbers and the square of the nth prime. Let p(n) denote the nth prime. We define:    

We prove that R(n) converges to zero as n tends to infinity, and we derive the asymptotic form:

This convergence is slow and observable, making the ratio particularly suitable for investigating the balance between prime density and prime growth. Experimental data up to n = 10^8 yield R(10^8) ≈ 0.02389717, which is in close agreement with the theoretical estimate 1 / (2 log(10^8)) ≈ 0.02714341.

1. Introduction

The distribution of prime numbers remains one of the most intriguing topics in mathematics. In this work, we introduce and investigate a novel ratio involving the cumulative sum of the first n primes and the square of the nth prime. Let p(n) denote the nth prime number. Define:

This ratio compares the total 'weight' of the first n primes against the square of the largest among them. Unlike other asymptotic prime functions, this formulation yields a quantity that decays at a moderate rate, offering insight into the interplay between summation and extremal growth.

2. Theoretical Estimate

From prime number theory, it is known that:     

and 

Substituting these into R(n), we obtain:

Therefore, R(n) tends to 0 as n tends to infinity, with a slow decay governed by the inverse of the logarithm.

3. Numerical Verification

For n = 10^k where k = 1, 2, ..., 8, we computed the following values of R(n):

{0.15338882, 0.08245496, 0.05872875, 0.04523687, 0.03685715, 0.03116178, 0.02704081, 0.02389717}

Similarly, using the theoretical estimate R_est(n) = 1 / (2 log n), we obtained: 

 {0.21714724, 0.10857362, 0.07238241, 0.05428681, 0.04342945, 0.03619121, 0.03102103, 0.02714341}

The plot below compares these two sequence

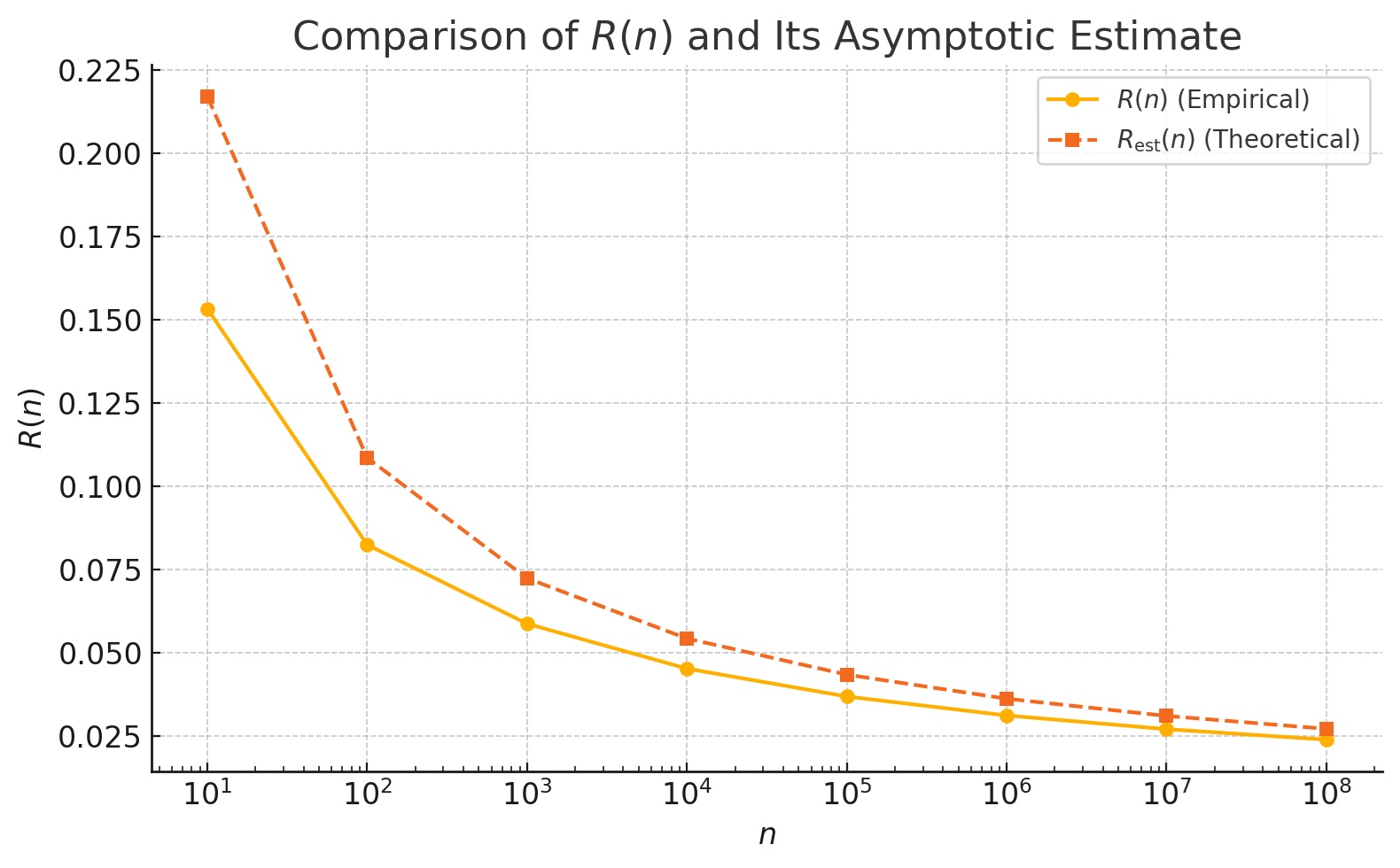
Figure 1. Comparison of empirical R(n) and its theoretical estimate R_est(n) over n = 10^k (k = 1,...,8).

Remark (Cosmological Analogy)

Interestingly, the ratio defined by

can be interpreted as the average density of a hypothetical universe. Here, the nth prime p(n) defines a characteristic spatial radius r(n) = p(n)^2/3, and the cumulative sum of the first n primes is treated as the total mass M(n) within that radius. Thus, R(n)  becomes proportional to the mass-to-volume ratio M(n)/V(n), where V(n)∼ r(n)³∼p(n)² .

As n → ∞, this yields a model with infinite spatial extent and unbounded total mass, yet with a vanishing average density — echoing Einstein’s early cosmological considerations.

In his 1917 paper 'Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie', Einstein introduced the idea that a universe with infinite spatial extension must have zero average mass density to remain consistent with the field equations. Later, in his 1921 lecture 'Geometry and Experience', he emphasized the challenge of inferring cosmic structure from local observations. These foundational insights resonate naturally with the asymptotic behavior of R(n) in prime number theory.

4. Conclusion

We have identified a new ratio R(n) based on prime numbers that asymptotically tends to zero at a logarithmic rate. This quantity reveals a contrast between additive accumulation and multiplicative extremality in the prime sequence. Its moderate decay makes it a promising candidate for further numerical and theoretical studies into the distribution of primes.

References

[1] G.H. Hardy and E.M. Wright, *An Introduction to the Theory of Numbers*, Oxford University Press.

[2] J. Barkley Rosser and L. Schoenfeld, *Approximate formulas for some functions of prime numbers*, Illinois J. Math. 6 (1962), 64–94.

[3] Pierre Dusart, *Estimates of Some Functions Over Primes without R.H.*, arXiv:1002.0442, 2010.

[4] A. Einstein, Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (1917).

[5] A. Einstein, Geometry and Experience, Lecture before the Prussian Academy of Sciences (1921).

[6] C. O'Raifeartaigh and B. McCann, Einstein's cosmic model of 1931 revisited, arXiv:1312.2192 (2013).