氧气在人体内运输的理论

THEORY OF OXYGEN TRANSPORT TO TISSUE - PMC

一、前言

氧气在细胞能量代谢中已知发挥着关键作用。氧化作用及其他形式的能量产生均依赖于向细胞持续供应氧气。在哺乳动物体内，氧气从肺部的大气中摄取，通过血液循环由血液输送到组织中，最终主要在线粒体内被利用。这一看似简单的过程背后，隐藏着诸多关于该路径不同环节中物质转运物理机制的问题：血液中的氧气主要通过单纯的对流作用转运吗？扩散和化学动力学又扮演着怎样的角色？氧气转运路径中各类膜结构（红细胞膜、内皮细胞膜、实质细胞膜）所产生的转运阻力有多重要？氧气是通过单纯扩散穿过这些膜，还是借助载体的易化作用实现扩散？细胞内的转运机制是什么？主动转运在氧气输送中是否发挥作用？血液与组织之间氧气交换的主要部位是小动脉、毛细血管还是小静脉？不同生理状态下、不同组织中，这些交换部位是否存在差异？目前，对于这些重要问题，我们尚未得出确切且全面的答案。清晰理解氧气在整个转运路径中的物理机制，是理解血流调节的前提。

克罗格（Krogh）¹⁰²为氧气向组织转运的理论奠定了基础。他提出，氧气在组织中通过氧张力（PO₂）梯度驱动的被动扩散进行转运，并构建了一个由单根毛细血管供血的“基本组织单元”的简单几何模型。该几何模型通常被称为“克罗格组织圆柱模型”，简称“克罗格模型”。克罗格与他的同事——数学家厄兰（Erlang）共同推导了描述组织圆柱内氧气扩散与摄取的微分方程。该方程的解将组织中的氧张力表示为组织圆柱内空间位置的函数。这个简单的方程被称为“克罗格方程”或“克罗格-厄兰方程”，在过去70年间一直是大多数生理学估算的基础。

后续在氧气向组织转运的定性与定量理解方面取得的重大进展，主要源于对以下领域的研究：氧-血红蛋白动力学、血红蛋白与肌红蛋白在促进氧气扩散中的作用，以及形态学和血流动力学异质性的作用。

本综述聚焦于氧气向组织转运的相关理论，力求全面系统地涵盖氧气分子往返于红细胞的整个路径——包括穿过血浆、内皮细胞、血管壁其他成分，以及通过细胞外和细胞内空间到达线粒体的过程。线粒体中的氧气转运未被纳入本综述范围，因为作为生物化学的重要领域（氧化磷酸化），其相关内容已在众多教科书和综述中有所阐述。本综述仅少量引用关于氧气转运的实验研究和生理学方面的文献，读者可参考韦贝尔（Weibel）¹⁸⁶近期的专著，以及多篇探讨氧气在骨骼肌、心肌³⁶和脑¹⁷⁸血流调节中作用的综述。

本综述阐述了活组织中氧气转运理论研究的最新进展。此前已有多篇综述探讨了该问题的不同方面及其他相关议题，包括活组织氧气转运的综合性综述，血红蛋白¹和肌红蛋白在促进氧气扩散中作用的综述，体外装置中血液氧合的综述²²、¹⁷²，以及角膜-隐形眼镜系统中物质转运的综述⁴³。为保证完整性，本综述涵盖了活组织氧气转运理论的所有重要方面；但对于已有近期综述涉及的领域（如血红蛋白和肌红蛋白促进氧气扩散），仅引用该领域的少量核心文献。本综述的重点在于建模的方法学问题，而非将模型应用于特定组织所得出的生理学结论——这类应用可作为单独综述的主题。

在整篇综述中，我们尽可能采用标准符号。但在部分情况下，图表中的符号与正文中的符号存在差异，因为并非总能便捷地对图表进行修改。对于这类情况，图表说明中会对符号含义进行解释。

本综述分为以下几个主要部分：血液中的氧气转运、组织中的氧气转运、从血管到组织的氧气转运模型、特定器官和组织中的氧气转运，以及疾病状态下的氧气转运。综述旨在为读者提供必要信息，帮助其评估氧气转运模型在生理学研究中的作用。

二、氧气与血红蛋白/肌红蛋白的反应-扩散现象

 A. 氧-血红蛋白平衡

在人体循环系统的正常生理状态下，每毫升血液约携带0.2毫升氧气。在动脉血中，约98%的氧气与红细胞内的一种蛋白质——血红蛋白可逆结合，其余氧气则以游离形式溶解在血浆和红细胞内的血红蛋白溶液中。因此，准确计算与血红蛋白结合的氧气量具有至关重要的意义。

某一介质溶解游离氧气的能力，可通过（本生）溶解度系数α来表征，其遵循亨利定律：

式中，O2代表溶解氧浓度，P代表氧分压（氧张力），即PO2。氧浓度的常用计量单位为摩尔/毫升；或在特定温度、大气压和空气湿度条件下，采用毫升/毫升。描述空气的一组标准条件为STPD（标准温度、压力、干燥条件）：标准温度（0℃）、标准压力（760托）、干燥（水蒸气压为0托）。另一组空气标准条件为BTPS（体温、环境压力、饱和水蒸气条件）：体温（人体为37℃）、环境压力、完全饱和水蒸气（在体温下，水蒸气压力为47托）。标注物理参数数值时，明确对应的条件至关重要。本综述采用STPD条件：1摩尔氧气（STPD）对应22400毫升氧气。血浆中氧气的溶解度系数典型值为α = 3x10^-5毫升氧气（STPD）/（毫升·托）。因此，在动脉血典型氧张力（P=100托）下，血液中的氧浓度为0.003毫升氧气/毫升血液。

几乎所有脊椎动物的血红蛋白分子均为四聚体，由4条肽链组成，每条肽链均结合一个血红素基团。血红蛋白的氧合过程是通过氧气与每个血红素基团中的铁（Fe）原子结合实现的。一个氧分子的结合会触发血红蛋白分子发生构象变化，进而影响其后续结合氧气或其他分子的能力。血红蛋白氧饱和度（S或SO2）指被氧气占据的可用氧气结合位点比例，通常以分数或百分比表示。本节探讨氧气与血红蛋白化学反应达到平衡时，血红蛋白-氧气饱和度与氧张力的关系；下一节将讨论动力学效应。

目前可估算血液以结合形式携带的最大氧气量：1毫升血液中约含0.15克四聚体血红蛋白（Hb4），其分子量约为65000。1摩尔四聚体血红蛋白可结合4摩尔氧气，据此可估算血红蛋白结合的氧气体积：（22400×4×0.15）/65000 = 0.201毫升氧气（STPD）/毫升血液。结合前文对血浆中溶解氧含量的计算，可得出血液携带的总氧气量为0.204毫升氧气/毫升血液——即若血红蛋白完全饱和，仅1.5%的氧气以溶解形式存在。

氧气与血红蛋白的化学反应受多种因素影响：温度、pH值、二氧化碳分压（PCO₂）以及2,3-二磷酸甘油酸（DPG）浓度²、¹¹⁸。在标准条件下（温度T=37℃$、血浆pH值pHplasma=7.4、二氧化碳分压PCO2=40托、2,3-二磷酸甘油酸浓度[DPG]=5毫摩尔/升），血红蛋白氧饱和度随氧分压变化的曲线呈S形，该曲线被称为氧合血红蛋白解离曲线（ODC）或氧-血红蛋白平衡曲线（OHEC）。上述变量均会影响氧合血红蛋白解离曲线的形状与位置¹¹⁸。血红蛋白达到50%氧饱和度时的氧分压被称为氧半饱和分压（P50）；人体血液的P50约为26托。该参数是衡量血红蛋白与氧气结合能力（亲和力）的指标：P50降低时，亲和力增强；P50升高时，亲和力减弱。

氧合血红蛋白解离曲线随二氧化碳浓度和pH值的变化被称为波尔效应（Bohr effect）。反过来，氧气与血红蛋白的结合也会影响其他物质的转运，其中，二氧化碳转运随氧浓度的变化被称为霍尔丹效应（Haldane effect）。

在氧气转运的数学建模中，获得“氧饱和度作为氧分压及其他参数的函数”的准确解析表达式至关重要。氧合血红蛋白解离曲线的数学表达式主要分为两类：一类源于氧-血红蛋白反应的动力学模型，另一类则是不依赖动力学模型、通过经验拟合得到的表达式。希尔（Hill）⁶³在“血红蛋白可结合4个氧分子”这一事实被证实之前，提出了首个氧-血红蛋白反应动力学模型:

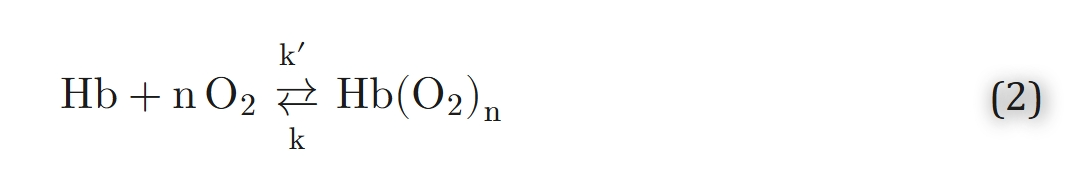
其中k′和k分别是结合速率系数和解离速率系数。在平衡状态下：

其中K=k′/k为平衡常数，[O₂]表示血红蛋白溶液中游离氧的浓度。根据亨利定律（方程1），我们可以将方程3改写为如下形式：

其中P50 = 1/（Knα）表示血红蛋白饱和度为50%时的氧分压值。当n≃2.7（对应人类血液）时，方程4在20%-80%的血红蛋白饱和范围内具有较高的准确性（见图1）。该方程被称为希尔方程，其中n为希尔参数。由于其简洁性，方程4在生理学和临床应用中最为常用。方程4还有一个便利特性：它能够轻松进行逆向推导:

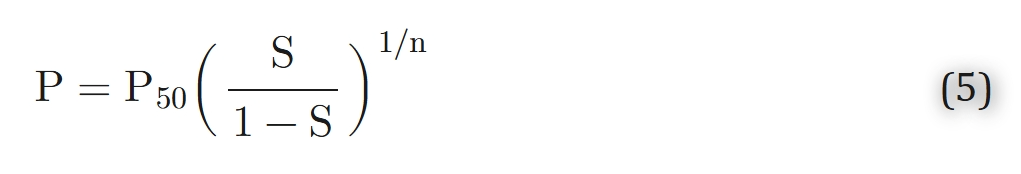
图 1.

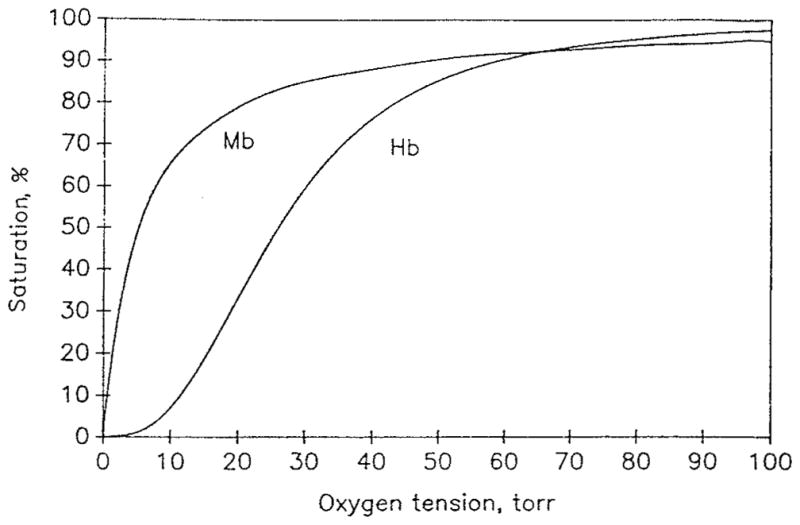
血红蛋白的氧解离曲线（公式4，P50=26托，n = 2.7)和肌红蛋白的氧解离曲线（公式24，P50=5.3托）。数学模型中出现的一个重要参数是氧合血红蛋白解离曲线的斜率；对于希尔方程

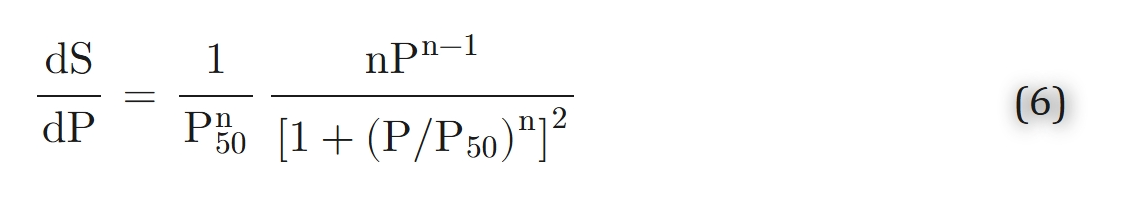
该函数的最大值Pmax小于P50:

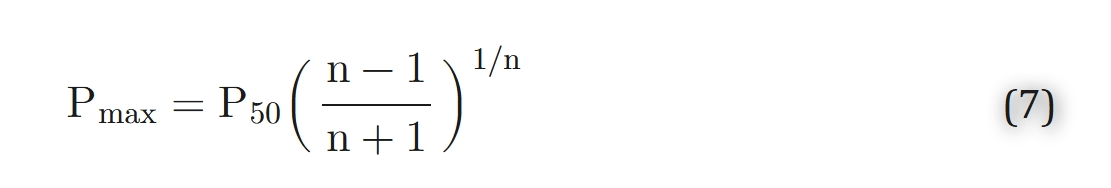
Adair1认识到每个血红蛋白分子包含四个血红素基团，因此可以形成含有一个、两个或三个氧分子的中间化合物（中间化合物假说）。他提出了一个四步化学反应：

在平衡状态下，方程8得到Adair方程：

其中S表示氧分子数与血红素基团总数的比值：

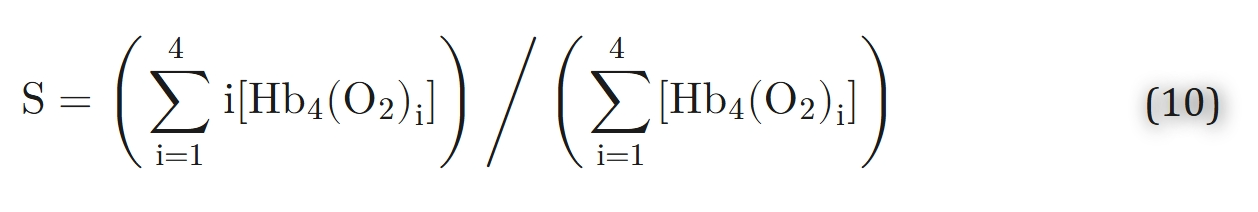
常数ai被称为阿代尔常数。它们可以用平衡常数Ki=ki′/ki表示，

Winslow等人针对PO₂在0至150托、血浆pH值在7.2至7.8、PCO₂在7至70托以及[DPG]在1至14毫摩尔之间的数据，编制了人体血液的系数ai表格。Hlastala等人报告了温度变化的影响。

方程9能准确描述氧分压（PO₂）广泛范围内的实验数据，但在组织供氧的数学建模中却鲜少被采用。其中一个可能的原因是该方程无法通过解析反演将P与S相关联。希尔方程和阿代尔方程都属于动力学模型范畴，具体可参考方程2和方程8。虽然已有更复杂的血红蛋白氧合动力学理论被提出30，但这些内容不在本综述讨论范围内。此外，还有多种氧解离曲线（ODC）的描述方法是通过实证拟合实验数据建立的，并非源自动力学模型。以下为氧解离曲线的表达式：15,16 

在0到95%的饱和度范围内，已被证明与Adair方程具有相同的精确性。方程12可逆地针对P进行求解：

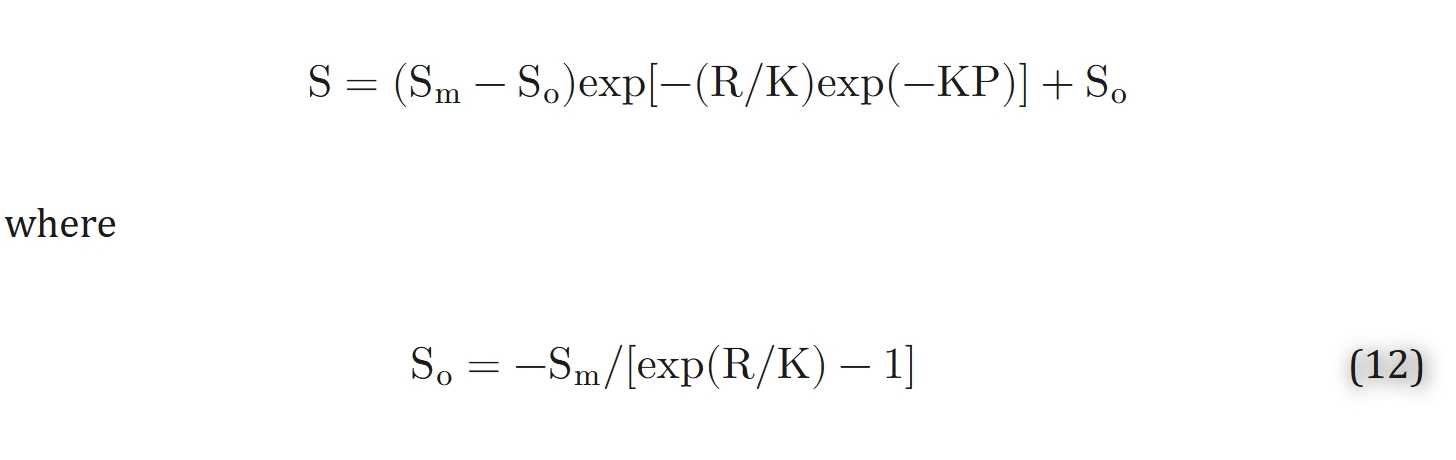
参数R和K的表达式（基于人体血液的PCO₂、pH值、[DPG]浓度及温度T）

对于人体血液，参数R和K可通过二氧化碳分压（PCO₂）、pH值、2,3-二磷酸甘油酸浓度（[DPG]）及温度（T）表示。

目前已有其他数学算法被提出，这些算法要么是对阿代尔方程（Adair equation）的修正[117]，要么与该方程无关联[88,161,170,173]。

 B. 氧-血红蛋白动力学

相较于前文讨论的氧-血红蛋白平衡关系，人们对氧-血红蛋白反应动力学细节的了解程度尚显不足。造成这一情况的原因主要有两点：一是该反应的特征时间极短（仅几分之一秒），导致动态测量难度较大；二是反应的动力学系数数量多于平衡系数。

希尔（Hill）提出的非整数n型化学反应（方程式2），尽管能为氧合血红蛋白解离曲线（oxyhemoglobin dissociation curve）提供实用表达式，但显然不符合实际情况。因此，研究人员尝试为氧-血红蛋白反应构建其他简单的动力学关系模型。在部分场景中，将动力学关系通过“含一个血红素基团的分子片段”（即血红蛋白分子的1/4）来表示会更为便捷，这类分子片段的摩尔浓度用[Hb]表示。最简单的氧-血红素基团一步化学反应（方程内容未完整给出）：

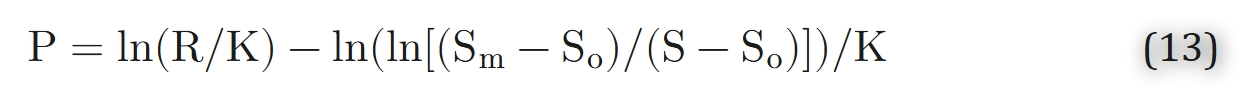
其中，常数反应速率系数k′和k分别对应于化学反应的速率

和以下动力学方程：

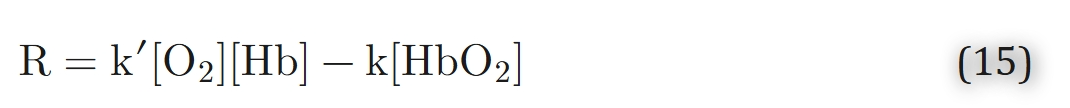
在平衡状态下，化学反应速率等于零，即R = 0。Gibson等人通过实验估算了人类血红蛋白在37℃和pH = 7.1条件下的系数k′和k，分别为k′= 3.5×10⁶M⁻¹s⁻¹和k = 44 s⁻¹。这些数值对应氧合半衰期t1/2 = 5至10毫秒。Middleman提出了对数据的另一种分析方法。然而，反应速率（方程15)导致双曲线而非S型的平衡关系（与方程3对比）。

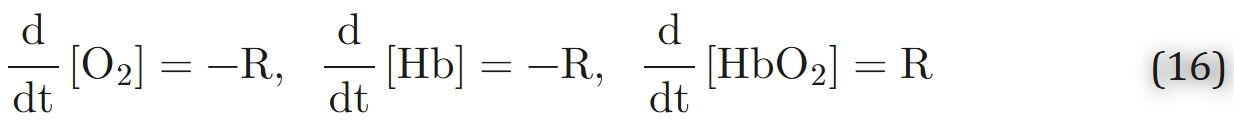
尽管与实验数据存在差异，但动力学模型（方程14)仍能有效描述反应初始阶段的系统特性。为克服这一缺陷，Moll123提出了可变速率系数模型：在该模型中，解离速率系数k保持恒定，而结合速率系数k′则被设定为氧分压的函数，使得S和P之间的关系简化为选定的平衡关系。例如，对于希尔方程4：

在多项氧运输分析中，采用变结合速率系数（方程18)的一步动力学模型（方程14)已被广泛应用。8,19,35,169同样地，通过合理选择k′(P)，该一步动力学方程可与任意形式的氧解离曲线（例如阿代尔方程）相匹配。195简而言之，可采用以下方法：要求方程15中的平衡条件R = 0与任意氧合血红蛋白解离曲线S = F(P)相一致，则可推导出：

如果假设k是常数，那么将S = F(P)代入方程19中，得到结合速率系数作为氧张力的函数，反应速率可表示为

古铁雷斯58提出了一个略有不同的动力学模型。他在希尔方程3中将希尔参数n定义为饱和度的函数，以拟合塞弗林豪斯的人体血液平衡数据。161方程17仍描述了k与k′之间的关系，但指数n是饱和度的函数。描述阿代尔中间化合物假说的化学反应（方程8）依赖于八个速率常数（结合反应和解离反应各四个，分别记为k′i和ki）。反应速率

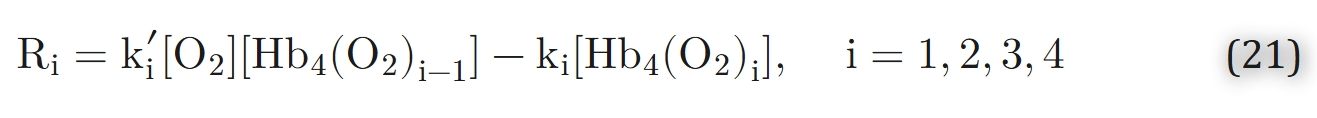
对应于动力学方程：

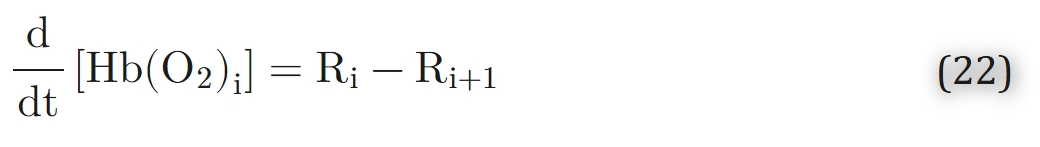
在化学平衡中，R1 = R2 = R3 = R4 = 0。

系数k′和k的测定及相关动力学分析

吉布森（Gibson⁴⁶）测定了21.5°C、pH=7.0条件下人体血红蛋白的系数k′和k，具体数值如下：k′₁=17.7×10⁴ M⁻¹s⁻¹；k₁=1900 s⁻¹；k′₂=33.2×10⁴ M⁻¹s⁻¹；k₂=158 s⁻¹；k′₃=4.89×10⁴ M⁻¹s⁻¹；k₃=539 s⁻¹；k′₄=33.0×10⁴ M⁻¹s⁻¹；k₄=50 s⁻¹。下文将探讨四步动力学在毛细血管内物质转运分析中的应用。

如前所述，由于血红蛋白分子发生构象变化，其一个位点与氧气的结合会与其他位点与其他物质的结合相互关联，这种现象被称为别构效应（allosterism）。具体而言，血红蛋白与氧气的结合会受到二氧化碳分压（PCO₂）、pH值、二磷酸甘油酸浓度（[DPG]）及其他因素的影响；反过来，氧气结合也会影响二氧化碳、氢离子等其他物质的转运。因此，通过考虑氧气、血红蛋白、一氧化碳、二氧化碳、氢离子以及相应反应中的中间化合物之间的同步化学反应，可更全面地描述氧气转运过程。需注意的是，在上述物质中，仅氧气和一氧化碳会竞争血红素基团中相同的结合位点，而其他分子和离子则结合于其他位点。望月（Mochizuki）及其同事在一系列论文中对相应的多物质转运方程进行了详细的数学分析。对这些过程的详细探讨超出了本综述的范围。

C、氧-肌红蛋白动力学

不同物种和组织中存在多种理化性质各异的血红蛋白分子。在脊椎动物红色骨骼肌和心脏中发现的组织血红蛋白被称为肌红蛋白（Mb）。肌红蛋白分子为单体结构，分子量约为16000至17000。不同组织中肌红蛋白的浓度差异显著，通常在0至1 mM的范围内。

与前文对血红蛋白溶液中溶解氧的讨论类似，我们可对单位体积组织中溶解氧和结合氧的量进行比较。假设组织氧分压（Pt）=20托（torr），氧溶解度系数（αt）=3×10⁻⁵ ml O₂/ml/托，则可计算出游离氧浓度[O₂]free=αt×Pt=6×10⁻⁴ ml O₂/ml。若组织中肌红蛋白浓度[MbT]=0.5 mM，那么在100%饱和状态下，与肌红蛋白结合的氧气量[O₂]bound=(0.5×10⁻⁶)×(22.4×10³)=11.2×10⁻³ ml O₂/ml，即约为游离氧浓度的20倍。

若假设运动中肌肉的耗氧率（M）=1.3×10⁻³ ml O₂/ml/s，那么可轻松估算出：若氧气供应中断，与肌红蛋白结合的氧气可维持的时间为[O₂]bound/M≈8秒。对于静息状态下的肌肉，其耗氧率可能会低一个数量级，因此肌红蛋白储存的氧气可维持一分钟以上。由此可见，肌红蛋白在氧气储存中发挥着重要作用，且能在血流短暂中断时起到“缓冲”氧气供应的作用。

由于肌红蛋白分子为单体，且仅有一个氧气结合位点，因此其与氧气的反应为一步化学反应。

具有恒定的结合和解离速率系数k′和k，对应于双曲线平衡解离关系：

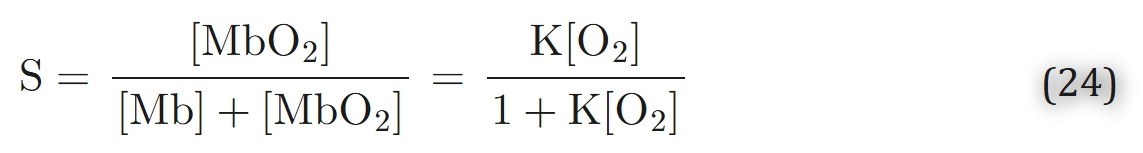
其中，K = k′/k 为平衡常数，S 为肌红蛋白与氧气结合的饱和度。令 K = (αtP50)⁻¹，可看出式（24）为 Hill 方程，且 Hill 系数 n = 1。该特性是肌红蛋白非协同性（noncooperativity）的体现，即每个结合位点均独立结合氧气。这与血红蛋白不同，血红蛋白具有协同性（cooperativity）——某个位点对氧气的结合会受其他结合位点结合状态的影响。

通常情况下，肌红蛋白的 P50（半饱和氧分压）显著低于血红蛋白：肌红蛋白的 P50 ≈ 5 托（torr），而血红蛋白的 P50 ≈ 26 托。因此，只有当组织氧分压（PO₂）降至 10 托以下时，肌红蛋白才会脱离完全饱和状态。图 1 展示了血红蛋白与肌红蛋白典型的平衡解离曲线。

D. 血红蛋白与肌红蛋白对氧气扩散的促进作用

物质以游离形式扩散时遵循菲克定律（Fick’s law）。该定律指出：单位时间内通过单位面积的物质总量（称为扩散通量），与垂直于该面积方向上的物质浓度梯度成正比，表达式如下：

比例系数D称为扩散系数。如果浓度c在三维空间中发生变化，那么菲克定律应该用矢量形式表示

扩散方程可以通过体积内的质量平衡推导，即体积内物质数量的时间变化率等于通过边界的净扩散通量加上体积内的化学反应速率。

若某物质能与另一种物质（即载体）发生可逆反应，那么该载体可通过结合形式转运该物质，从而增强或促进该物质的分子转运。这种转运形式被称为载体介导转运（carrier-mediated transport）或载体易化转运（carrier-facilitated transport）（Schultz 等人，159）。血红蛋白与肌红蛋白可作为氧气的载体，因此存在血红蛋白易化扩散和肌红蛋白易化扩散两种氧气转运方式。目前已有大量文献（包括实验研究与理论分析）探讨血红蛋白和肌红蛋白对氧气转运的促进作用，且关于该主题的深度综述亦已发表。

为阐明血红蛋白对氧气转运的易化作用，可考虑如下场景：氧气在一层“血红蛋白溶液平板层”中扩散，该溶液层由两层膜界定——这两层膜仅允许氧气透过，而不允许血红蛋白透过。在红细胞内典型的血红蛋白浓度下，氧气的扩散系数DO=0.95×10^-5平方厘米/秒，而血红蛋白的扩散系数DHb=1.44×10^-7平方厘米/秒。（由于扩散系数主要由分子量决定，且氧气分子远小于血红蛋白分子，因此可认为还原态血红蛋白与结合态血红蛋白的扩散系数相同。）由此可知，血红蛋白分子的扩散速度约为游离氧气分子的1/65。

那么，扩散速度如此缓慢的血红蛋白，为何能显著影响氧气转运？原因在于：与血红蛋白结合的氧气量远高于游离氧气量（根据前文估算，在氧分压P=100托时，结合氧约为游离氧的70倍）。从数学角度，可将氧气的总扩散通量表示为游离态与结合态通量之和：

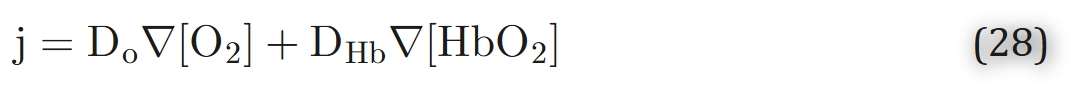
如果我们假设溶液中血红蛋白的总浓度[HbT] = [Hb] + [HbO2]是均匀的，我们可以将方程28改写为：

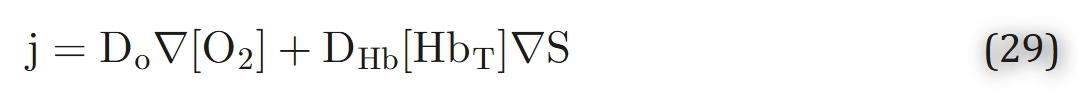
假设氧与血红蛋白之间的化学反应处于平衡，因此二者浓度之间的关系由氧合血红蛋白解离曲线所控制，我们得到：

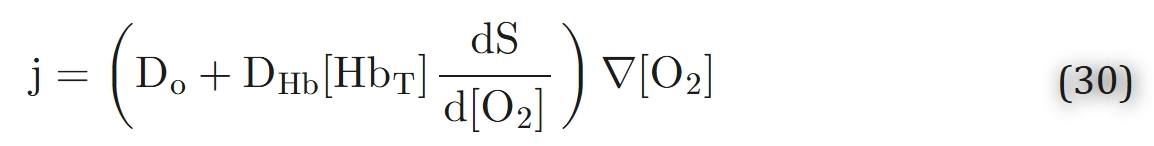
括号中的表达式可视为有效扩散系数Deff。通过方程1，我们得出结论：氧的扩散被增强了一个因子。

假设血红蛋白总浓度为[HbT] = 20.3毫摩尔/升（mM）= 2.03×10⁻⁵摩尔（血红素单体）/毫升（此浓度对应34克/分升（g%）的血红蛋白溶液），且血红蛋白溶液中氧气的溶解度系数为α = 1.56×10⁻⁹摩尔/（毫升·托）。若希尔方程的参数为氧半饱和分压（P₅₀）= 26托（torr）、希尔系数（n）= 2.7，并取氧合血红蛋白解离曲线在氧分压（P）= 19.5托处的最大斜率（见公式6和公式7），则由公式31计算得出的最大扩散增强倍数为有效扩散系数与氧气扩散系数之比（Dₑff/Dₒ）= 6.9。

对于肌红蛋白，由希尔系数n=1时的公式6可知，其氧饱和度对氧分压的斜率（dS/dP）在氧分压P=0时达到最大值。因此，氧分压P的值越小，扩散增强倍数越大。例如，假设肌肉组织中肌红蛋白的扩散系数（Dₘᵦ）= 1.5×10⁻⁶平方厘米/秒（cm²/s）、氧气的扩散系数（Dₒ）= 2×10⁻⁵平方厘米/秒、氧气溶解度系数α = 1.35×10⁻⁹摩尔/（毫升·托）、肌红蛋白总浓度（[MbT]）= 0.5毫摩尔/升（mM）、肌红蛋白氧半饱和分压（P₅₀）= 5.3托，则当氧分压P=2托时，扩散增强倍数（Dₑff/Dₒ）= 3.7；当氧分压P=0.5托时，该倍数为5.4。

然而，并非溶液层内所有区域都满足化学平衡假设。若反应达到平衡，则氧合血红蛋白浓度梯度可通过氧张力梯度表示为：

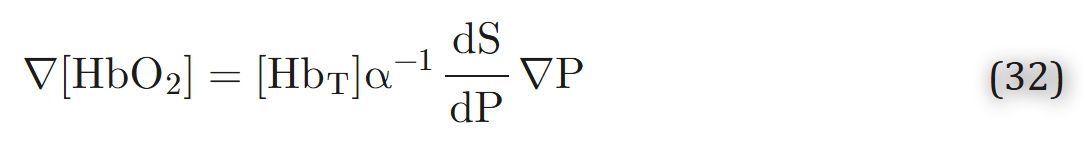
但该边界对血红蛋白分子是不可渗透的，因此在边界处，氧合血红蛋白浓度的法向导数（∂[HbO₂]/∂n）等于0；而氧分压的法向导数（∂P/∂n）与穿过该层的氧气通量成正比，因此不为0。这表明，在该层的边界附近，“反应处于平衡状态”这一假设并不成立。这种化学反应未达平衡的区域被称为边界层（boundary layers）。此时，浓度分布取决于边界层的特征厚度与血红蛋白层厚度的比值。

边界层的概念常见于多种物理现象的分析中，且通常与一个无量纲小参数相关（例如，在流体力学中，当雷诺数较大时会形成边界层，因此雷诺数的倒数就是一个小参数）。特征长度Lβ = (DOk′[HbT])^(1/2)（即DO、k′与[HbT]乘积的平方根）是衡量“远离化学平衡状态的边界层”厚度的指标。该问题的特征几何尺寸（对于扁平层而言，即层的厚度）L与Lβ的平方比被称为**达姆科勒数**（Damköhler number），表达式如下：

该参数也可定义为氧扩散特征时间（τ_DO = L²/D_O）与反应特征时间（τ_KO = (k′[Hb_T])⁻¹）的比值。当γ ≫ 1时，溶液主体处于平衡状态，非平衡区域仅局限于边界附近的薄层内；相反，当γ<<1时，整个血红蛋白溶液层均远离平衡状态。载体促进扩散问题将在后续章节中，结合红细胞释氧及肌纤维内扩散的背景进行更详细的探讨。关于载体促进转运问题的最新通用数学分析，可参考Hoofd与Kreuzer[73]、Kollka与Salathe[95]以及Hoofd[75]的研究成果。