学数学的时候, 我们经常会听说xx基本定理. 比如算术基本定理, 它是初等数论中的基本定理, 其最早的证明是由欧几里得在几何原本里给出的. 算术基本定理又称为正整数唯一分解定理, 它说明了素数是自然数的基本砖块, 任何正整数都可以唯一地分解为有限个素数的乘积.

代数基本定理是代数学中的一个基本定理, 它是关于多项式的基本定理, 它说明任何复多项式都可以唯一地分解为有限多个一次多项式的乘积. 代数基本定理的第一个证明是由法国数学家达朗贝尔给出的, 但证明不完整. 接着, 欧拉也给出了一个证明, 但也有缺陷. 拉格朗日于1772年又重新证明了该定理, 后经高斯分析, 证明仍然很不严格的. 代数基本定理的第一个严格证明通常认为是高斯给出的(1799年在哥廷根大学的博士论文).

在分析学领域, 有微积分基本定理, 它指出了微分和积分之间自然的互逆关系.

这些定理就像化学中的元素周期表, 粒子物理中的标准模型一样, 是一个领域最基本的规律.


本文要谈的是我在图论领域发现的一个定理, 它是建立因果凝聚框架的基石. 我认为它的意义和前面提到的几个基本定理非常相似, 所以我把它叫做图论基本定理, 它的意义将会随着因果凝聚理论的应用发展而逐渐显现. 未来将会说明它完全应得这个名字.图是一种常见的数学对象, 也是一种最基本的组合结构. 大多数人都把图理解为一种邻接关系或者一种一维的几何对象. 但是, 在我眼里, 它本质上却是像多项式一样的代数结构, 我把图看作是张量多项式. 我要科普的是图论基本定理, 它揭示了图论中的基本构造和张量演算的基本语法之间的严格对应关系, 是图论和张量范畴理论, 非微扰量子场论, 凝聚态物理, 以及人工智能理论的内在的深刻联系.要科普这种本质上的理解, 我们需要从阿尔伯特.爱因斯坦的数学发现谈起.
1. 爱因斯坦求和约定
1916年, 在建立广义相对论的论文中, 爱因斯坦在里奇和列维-茨维塔约定的基础上, 引入了后来以他名字命名的求和约定, 即爱因斯坦求和约定. 这个约定是他在大量的张量演算中发现的规律, 可以说是爱因斯坦对数学最大的贡献. 爱因斯坦曾跟朋友半开玩笑地说:"这(求和约定)是数学史上的一大发现, 若不信, 可以试着返回那不使用这方法的古板日子." 爱因斯坦的求和约定使得人们可以在复杂的矩阵和张量计算过程中避免使用连加号, 从而大大降低了张量运算表达式的复杂性并提高了张量运算的直观性. 事实也正如爱因斯坦所言, 这个约定现已成为数学家和物理学家处理哑指标求和, 或者哑变量积分的标准方法.


2. 多线性映射的复合
数学家把张量理解为多线性映射, 他们喜欢简洁的概念推理, 因此倾向于用坐标无关的方式表示张量. 物理学家喜欢用指标分量的形式表示张量, 因为这样更有利于具体计算. 在指标分量的表示中, 指标表示线性空间的基向量. 当用指标形式计算张量复合的时候, 需要用到多重求和号. 使用爱因斯坦约定则可以省略掉多重求和号. 爱因斯坦求和约定背后一个更重要的规律是这个约定和各个线性空间的基底或者坐标系的选择无关, 因此它是一种背景无关的规律.

3. 狄拉克括号
保罗.狄拉克是一位天才物理学家, 量子力学和量子场论先驱. 他发明了著名的狄拉克括号, 这是一种基底无关的向量表示方法, 分别用右矢和左矢来表示列向量(态矢量)和行向量(共轭态), 给量子力学提供了一种抽象简洁的算符表示形式. 但是在表示高阶张量和量子纠缠的时候, 狄拉克括号仍然不够直接, 直到图形演算形式的出现, 才得到最优表示(参考,ZXW calculus).

4. 费曼图
在爱因斯坦和狄拉克之后, 接下来出场的是大名鼎鼎的物理天才理查德.费曼, 他发明了量子力学的路径积分原理和对微扰量子场论非常重要的费曼图. 在此强调一下, 费曼有一位天才学生, 史蒂芬.沃尔夫拉姆, 他是一位集计算机科学家, 数学家, 物理学家和企业家于一体的犹太人, 是广泛流行的数学软件Mathematica和计算知识引擎Wolfram Alpha的主要设计师, 可谓是科学和商业领域的"双料巨人", 被称为当今世界上最聪明的人. 他对我的因果凝聚理论很感兴趣, 特别是他的计算科学纲领中的因果不变原理和因果凝聚思想可以说是不谋而合.

除了沃尔夫拉姆, 斯莫林, 洛韦利, 贝兹, 和卡里普这些真正对量子引力感兴趣的理论物理学家都对因果凝聚框架感兴趣.


说回费曼, 为了简化路径积分的微扰计算, 在1948年, 他发明了著名的费曼图方法, 并给出其粒子-时空解释. 费曼图和其粒子-时空解释使得微扰量子场论的物理图像非常直观, 并使得微扰计算的规则更加容易理解, 大大简化了物理学家在做微扰计算时的工作量, 让微扰量子场论变得简单易学.

5. 彭罗斯图示法
费曼图是物理直觉和数学逻辑严密结合的产物. 可以说, 费曼图和狄拉克符号在量子物理中的重要性完全类似于爱因斯坦求和约定在微分几何和广义相对论中的重要性. 但是事情的美妙不止于此, 可能爱因斯坦也无法想象, 他的求和约定竟然和费曼的图形语法在本质上是一回事. 揭开这个奥秘的是另外一位数学物理天才, 罗杰.彭罗斯. 他是目前唯一一位获得诺贝尔物理学奖的数学家(相反的, 威腾是目前唯一一位获得菲尔兹奖的物理学家). 彭罗斯的导师是几何学家霍奇, 他提出了代数几何中著名的霍奇猜想, 这个猜想联系了微分几何和代数几何, 它是克莱数学研究所设立的七个千禧问题之一. 彭罗斯是一位非常善于形象思考的数学物理学家. 1952年, 在学习广义相对论的过程中, 他发现了爱因斯坦求和约定背后更加抽象的规律, 发明了张量的抽象图示法. 彭罗斯图示法可以看作是爱因斯坦求和约定, 费曼图方法和狄拉克括号的统一.

彭罗斯引入了弦图这一个重要的图形化工具, 它用蜘蛛图(单顶点弦图, 也叫素图)的顶点表示张量, 蜘蛛图的腿表示张量的指标, 张量的缩并用蜘蛛图腿的连接表示. 彭罗斯的方法特别适合描述张量的缩并. 由于印刷技术的困难, 彭罗斯的图形表示法直到1971年才发表. 彭罗斯把他的图示法抽象为关于"抽象张量系统"的理论, 使得张量运算和求和约定成为一个纯形式的符号理论.

6. 自旋网络
继费曼之后, 彭罗斯是第二位让图形获得物理意义的数学家. 在1955年, 惠勒提出量子泡沫的思想, 意图刻画量子引力的微观起伏. 1971年, 彭罗斯提出了自旋网络的概念, 意图刻画空间量子的微观组合结构. 惠勒的量子泡沫和彭罗斯的自旋网络可以说是异曲同工, 为量子引力的后续发展提供了思想框架. 自旋网络是一种特殊的张量网络, 其特点是在每一条边上标记的都是某个对称群的不可约表示. 在一定意义上, 我们可以认为自旋网络就是张量的不可约表达式(类似于自然数的素因子分解和多项式的不可约分解). 自旋网络有深刻的数学和物理含义, 它广泛地出现在群表示论, 格点规范理论, 拓扑场论, 圈量子引力, 弦网凝聚理论等的研究中. 要彻底看透它的意义应该在重整化群的角度才是可能的. 彭罗斯对自旋网络的早期设想, 也已经在20多年后, 1994年, 被洛韦利和斯莫林给实现. 他们证实了彭罗斯发明的自旋网络恰好是量子引力中几何算子的本征态. 这一成果标志着圈量子引力的正式诞生. 在我的因果凝聚框架下, (广义的)自旋网络也是自然而然地出现的, 它们是范畴学构造的自然结果. 这一事实, 对我来说, 也是一个令人感到不可思议的奇迹. 在此提一点, 彭罗斯的扭量哲学可以看作是因果凝聚的本体论基础.

7. 张量范畴和平面弦图
1965年, 德国数学家和计算机科学君特.霍茨用张量范畴描述开关电路的语法和语义, 首次给出了平面弦图的定义, 将它们作为自由张量范畴中态射的拓扑表示.

8. 图形演算的数学基础
1988-1991, 范畴学家乔亚尔和斯特里特奠定了图形演算的数学基础.
1990, 范畴学家鲍尔首次建立了图论和图形演算的本质联系.

9. 什么是图形演算
正如前面所言, 彭罗斯的图示法统一了爱因斯坦求和约定, 费曼图规则和狄拉克括号, 它是张量演算的一般语法. 但是, 彭罗斯的图示法并不是这个理论的顶峰, 它仍然可以在更广泛的情景下有效. 比如前面提到的霍茨就在开关电路的语境下重新发明了平面弦图, 并把理论抽象到张量范畴的层次.事实确实如此, 张量运算的规律在整个科学领域都是有效的, 并不仅仅拘限于线性代数, 微分几何和量子力学, 在计算机科学, 逻辑学, 语言学, 化学, 生物学等等领域都有它们的影子. 这也是一个新兴学科"应用范畴学"正在迅速发展的原因, 国外的范畴学家们正在积极抢占其它科学领域中一切可以范畴化的结构.现在我们已经很清楚, 彭罗斯的"抽象张量系统"应该进一步抽象为张量范畴(或者称为幺半范畴)和对称张量范畴(或者称为置换范畴), 其中张量范畴上的演算是在平面和球面上的, 而对称张量范畴的演算是在高亏格曲面上的. 此处应该强调, 张量范畴和对称张量范畴并非什么可怕的抽象怪物, 而它们恰恰是我们日用而不知的东西. 我们的逻辑, 语言, 计算, 证明, 等统统都是它们的特例, 甚至类比, 想象也可以在它们的框架下来表示. 我们研究的数学结构统统都是按照它们的语法而组织的, 甚至可以说它们的存在比集合概念还要广泛. 当然, 这也是我强调应该以张量范畴作为人工智能数学基础的一个主要原因, 这是后话, 以后再详细解释.

我们应该像彭罗斯那样思考张量演算背后的"元理论"或者"语法". 为此,我们应该把张量仅仅理解为张量范畴中的态射, 而不用在意其具体意义, 我们需要研究张量演算的纯形式规律.张量演算本质上是一种平面演算, 其形式非常类似于初中学过的多项式理论.

张量的演算和数字的演算有完全平行的关系, 正如下表所列举的, 张量的复合运算(串联)相当于数字的加法运算, 只不过一般没有交换律, 但是结合律仍然保持. 恒等态射的地位则和数字0是相当的. 张量的张量积运算(并联)相当于数字的乘法运算, 只不过一般没有交换律, 但仍然满足结合律, 其中单位对象的作用和数字1是相似的. 在数字系统中, 加法和乘法满足分配律, 它反映了两种运算的相容性, 而在张量范畴中, 复合运算和张量积运算之间的相容性则是通过所谓的中间-4-交换律来体现的, 更本质的说法是, 它反映了张量积运算的函子性. 通过数字的加法和乘法这两种运算, 我们可以形成多项式, 类似地, 通过张量的复合与张量积, 或者说, 串联与并联, 这两种运算, 我们可以形成张量多项式, 只不过, 我们可以用一个平面定向图来直观的表示它, 更专业的术语叫做"渐进平面图". 所有的关于数字的多项式可以构成一个代数系统, 其中最重要的一个运算就是合成或者复合, 这是我们高中数学中最简单的复合函数的例子. 同样地, 张量多项式的系统上自然地也应该存在合成运算, 那么它是否有一个好的图形表示呢? 答案是肯定的. 在我的博士论文中, 我发现张量多项式的合成恰好可以用图的粗粒化来描述.

这个发现不是凭空而来的, 是我思考几个月之后无果, 而突然受到物理学家工作的启发而得到的. 这个发现过程完全可以用"踏破铁鞋无觅处,得来全不费功夫"来描述. 在圈量子引力理论中, 洛韦利等人考虑了几何量子的测量问题(https://arxiv.org/abs/1404.1750), 他们发现几何量子态的测量不是绝对的, 而是与坐标系的选择有关. 而在圈量子引力理论中, 坐标系的选择自然地和粗粒化构造相关. 一个形象的比喻就是我们用收音机接收电磁波信号, 频道的选择决定了接收信号的强弱. 几何量子态的测量也遵从类似的规律. 这可能也是所有背景无关的量子理论的特点.
无独有偶, 完全相同的粗粒化构造在弦网凝聚理论和张量网络重整化理论中也自然出现了. 这是一个很好的兆头, 说明我无意间触摸到了一个本质的东西, 后来的发展也确实如此, 因果凝聚框架的建立证明了这一点.



张量多项式和数字多项式的类比是系统的, 全方位的, 我们可以看到范畴学家计算张量多项式的方式和我们计算多项式的方式也是完全一致的, 其中范畴学家的切片方法和多项式的齐次化分解是完全对应的.
10. 为什么要用图形演算?
为什么要用图形演算? 如果你是像彭罗斯和费曼那样, 喜欢形象化思考的人, 那答案不言自明. 但如果不是也不要紧, 数学家给出了充足的理由. 如下图所示, 当我们要考虑两个张量多项式是否相等的问题时, 图形演算的优势就体现出来了. 因为我们的大脑并不擅长张量演算的形式法则, 但如果把这些法则形象化, 我们就很容易理解了. 图形演算的好处就是把张量演算的形式规则恰到好处地翻译成了平面图的同痕形变, 这是对人类是很友好的方法.

但是, 凡事有利必有弊. 反过来思考, 如果我们想用计算机帮助我们判断两个张量多项式是否相等应该怎么办呢? 显然, 计算机不会直观的感受平面图的拓扑形变, 因此这种对人直观的优势就成了对计算机不友好的劣势了. 不过, 没有关系, 我们可以彻底地解决这个问题, 因为张量多项式还有一套完全组合的描述, 这也是我们发现的. 但是我要在后面的文章中, 系统地介绍它.
11. 图形演算的拓扑性
现在我们可以回答为什么图形演算具有拓扑性质. 前面说过, 图形演算的好处是把演算规则自然地融解到语言的内在结构之中. 首先, 中间-4-交换律和张量积的结合律, 复合的结合律都翻译成为对图像的不同切割方式.

其次, 对于恒等公理和单位公理, 我们需要引入新的图形演算约定. 恒等公理的约定称为恒等约定, 它允许我们随意地添加或者删除一个度数为2的顶点(一条边内部的顶点), 前提是只要这个顶点上标记的是一个恒等态射. 正如前面所讨论过的, 恒等态射相当于数字0, 在一个数字表达式中我们可以随意地加一个数字0, 也可以减掉一个数字0, 这就是恒等约定地代数意义.对于单位公理, 它对应的约定称为单位约定, 它允许我们随意地添加或者删除一条边, 前提是只要这条边上标记的是一个单位对象. 因为单位对象相当于乘法的单位元, 即数字1, 所以在一个表达式中我们可以随意地乘以一个数字1也可以随意地除以一个数字1. 恒等约定的意义也是如此. 恒等公理和单位公理允许我们修改图的组合结构, 从而修改其拓扑结构.

最后, 当我们把恒等约定和单位约定与中间-4-交换律结合起来使用的时候, 有意思的事情就出现了. 它们分别意味着我们既可以上下移动平面图的顶点, 也可以左右移动源点和汇点的位置, 这就是图形演算的拓扑性的来源.

12. 更本质的理解
我们有两个层次上来理解多项式全体. 一个层次就是加法和乘法的层次, 多项式全体关于加法和乘法是封闭的, 这是一个线性的层次. 事实上, 多项式全体构成一个结合代数, 它具有泛性质, 是一个自由结合代数. 另一个更高的层次是复合的层次, 多项式关于复合是封闭的. 但是, 复合运算不是线性运算, 因此这是一个非线性的层次. 事实上, 多项式全体关于复合运算形成一个operad, 叫做结合operad. 这两个层次的观点自然是有关系的. 事实上, 在operad范畴和结合代数的范畴之间存在一个伴随, 这个伴随把一个operad对应到它的泛包络结合代数, 反过来, 每一个结合代数都可以看作是一个operad. 这一图景, 对于张量范畴也是类似的. 在张量范畴的情形, 所有的渐进平面图也构成一个自由张量范畴. 这是第一种层次的理解. 第二种层次的观点, 就是要把所有的渐进平面图的复合运算考虑进来,也就是细粒化操作, 这样就会得到一个monad(单子), 我把这个monad称为粗粒化单子, 它控制着所有的张量范畴. 张量范畴就是粗粒化单子的表示, 因此也可以把张量范畴叫做粗粒化代数. 这样一种描述更加接近于彭罗斯的"抽象张量系统"的公理化定义.

在2014年, 我发现了这个粗粒化单子, 并把它和格点规范理论和凝聚态物理中的重整化群联系了起来. 在这种物理的观点下, 张量范畴就变成了粗粒化不动点, 这可以看作是对文小刚的"拓扑序=张量范畴"这一拓扑序基本定理的一个数学证明. 当然, 这里面仍然有一些数学细节需要完善.

13. 对称张量范畴及其约定
张量范畴的公理对于描述现实世界太少了一点, 我们的现实需要更多的数学结构来描述. 事实上, 对称张量范畴是一个更好的描述现实的工具. 在2009年, 贝兹和他的学生斯泰一起写了一篇综述文章, 题目叫做 "物理,拓扑,逻辑和计算:一个罗塞塔石碑" (https://arxiv.org/abs/0903.0340). 这个文章的主角就是对称张量范畴, 说明了它在物理, 拓扑, 逻辑和计算领域中作为基础模型的角色. 文章强调的是对称张量范畴对这些领域进行统一的能力, 这也是罗塞塔石碑这一隐喻的意义. 在数学内部, 对称张量范畴的统治力是不言而喻的. 贝兹他们强调的是对称张量范畴在数学外部的统治力, 我认为这篇文章可以看作是应用范畴学开始的标志.
什么是对称张量范畴? 如下图所示, 它是具有对称结构的张量范畴. 在对称张量范畴中, 在某种意义上, 我们可以交换张量积的次序, 或者, 更严谨地说, 我们可以系统的比较不同次序的张量积所得的结果, 但是有一个限制, 那就是不同次序的张量积结果可以不同, 但是一定要是同构的, 也就是说, 比较是双向的, 平权的. 在我们的现实世界中, 很多系统都是这样运作的, 比如财富, 信息, 语言, 逻辑, 计算, 时空中发生的各种物理过程, 等等, 甚至我们勾心斗角的过程(博弈论)也可以用它来描述.

对于对称张量范畴, 由于多了一个对称结构, 我们自然需要比张量范畴更多的约定, 它们是对称约定和交换一致性约定. 由于这两个约定, 对称张量范畴的图形演算就不仅仅局限于渐进平面图了, 而是需要画在高亏格曲面上的因果网络了. 这一事实, 也启示了因果凝聚和弦理论的某种联系, 这是以后要讨论的内容.

14. 图论基本定理
现在终于可以说到本文的主角, 图论基本定理. 简单地讲, 它就是要把前面提到的图形演算约定换另一种说法来表述. 对称张量范畴的图形演算约定一共有八种. 除了最后的两种, 对称约定和交换一致性约定, 其余六种都可以用态射的语言来描述. 这最后的两种, 在因果凝聚框架里, 变成了规范等价的概念.我的贡献就在于引入了因果网络范畴, 实现了这种翻译. 比如, 恒等约定, 我们可以用图论的语言, 说成边的重分操作, 它恰恰是一种最基本的态射(见下图). 单位约定, 用图论的语言, 就是加边操作, 它也是一种基本态射. 把恒等约定和单位约定联合起来, 就是加孤立点的操作, 它也是一种基本态射. 这三种操作都是贝兹首先考虑的, 它们描述了图嵌入的三种基本模式. 不难发现, 态射的方向和约定的方向是相反的.

为了构造因果凝聚框架, 我认为仅仅考虑图的嵌入是不够的, 必须考虑图的粗粒化操作. 事实上, 一种有三种的基本的粗粒化操作, 它们分别是两点的合并 (表示的是两个态射的张量积运算), 两边的合并(表示的是两个对象的张量积运算)和边的收缩(表示的是两个态射的复合运算). 这三个操作, 都恰好可以用三类基本的态射表示. 表示它们的态射方向和图形演算约定的方向是相同的.

图论基本定理说的是任何两个图之间的任何态射都可以分解为三种基本态射的复合, 这就说明了图的态射对于图形演算的封闭性, 因此我们就可以用因果网络范畴来完全地描述张量演算, 因果凝聚框架的建立恰恰证明了这一点.


因果网络范畴的成功代表了范畴学思想的成功, 这个新思想既为图论带来了新的秩序, 也为范畴学带来了新的理论构造(广义minor理论). 这种范畴化的观点, 为图论研究带来了新的视角. 图论基本定理证明了图论操作, 图的态射, 张量演算之间的内在一致性. 在因果网络范畴中, 我们可以刻画图论中的各种操作, 比如粗粒化, 着色, 合并, 收缩, 浸入, 强浸入, 拓扑次图, 拓扑嵌入, 重分等. 如下图所示, 我们可以对图的操作进行有序的分类. 特别地, 粗粒化态射恰恰就是因果网络范畴中的余等化子, 这说明对称张量范畴可以被几何地理解为因果网络范畴上的一种广义测度, 这和贝兹构造的精神是完全一致的.


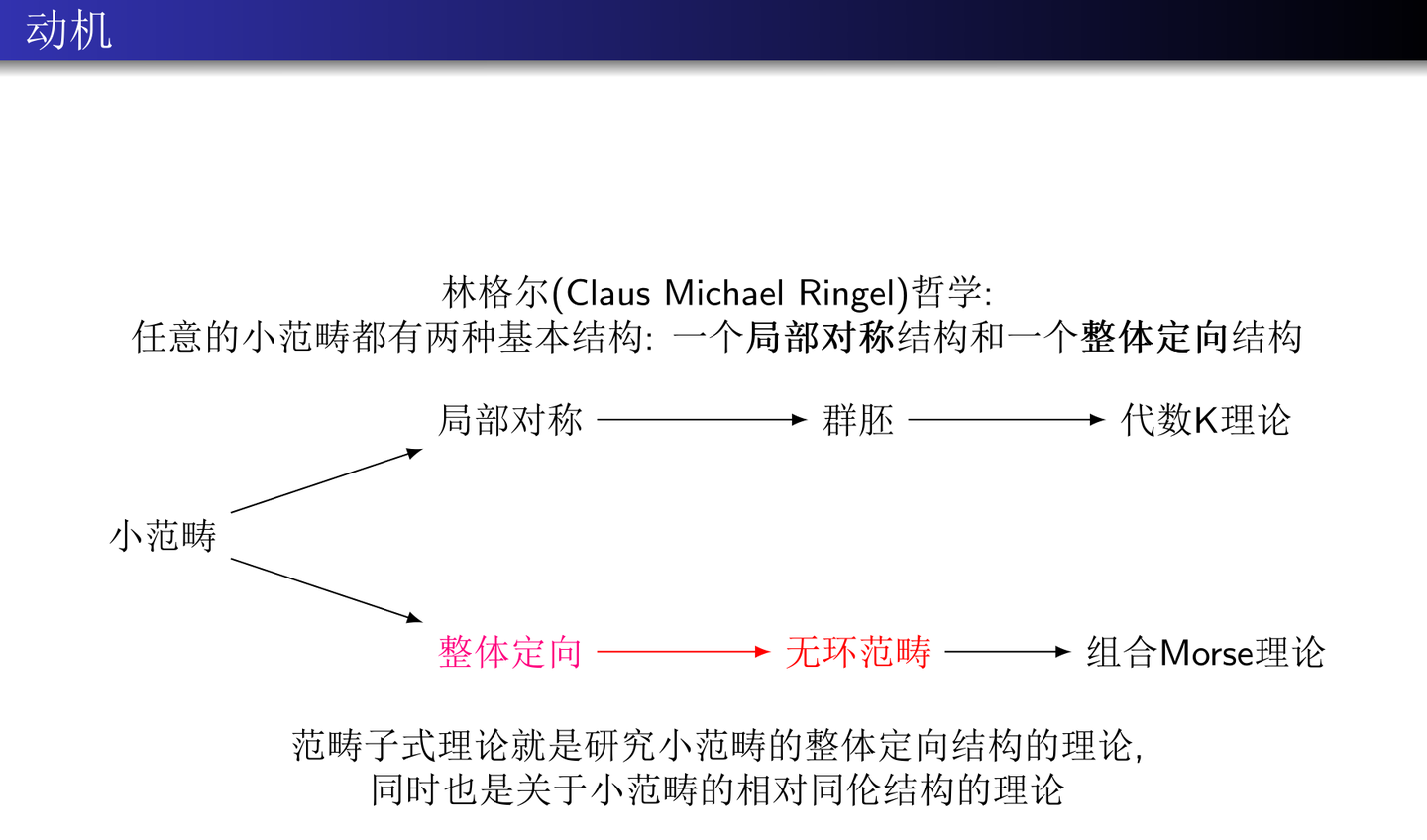
最后, 我们简单地提一点范畴化minor理论. 通过对因果网络范畴的研究, 我意识到一个更加一般的范畴学构造, 它可以把图论中的minor概念推广到一般的范畴中去, 从而实现了一个我很早就了解到的哲学. 这个哲学是代数学家林格尔(Ringel)提出的. 这个哲学是理解奥斯兰德双射(Auslander bijection)正确视角. 我认为我发展的广义minor理论可以认为是林格尔哲学的自然推广. minor本来是图论中的一个技术性概念, 我们缺乏对它的结构性理解. 现在我们可以把minor解释为因果网络范畴中的子商的概念. 子商是代数学家关心的概念(它涉及到的是一个代数结构如何由更小的代数结构组合而成), minor是图论学家关心的概念(它涉及到的是一个大图所包含的具有特殊性质的小图), 现在我把这两个概念统一起来了. 这个统一能够为数学带来什么变化, 现在还难以评估. 但是, 它确确实实实现了林格尔的哲学.

林格尔的这个哲学非常简单. 对于任何一个小范畴, 都有两种基本的派生结构:一个是相伴群胚, 它刻画了小范畴的局部对称性; 另一个是所谓的整体定向性, 在代数表示论中,奥斯兰德双射(Auslander bijection)和由模确定的态射(morphisms being determined by modules)可以认为是对这一观念的早期探索. 数学中有两种基本观念, 对称和非对称. 这两种观念用两种数学结构来描述, 对称用群(group)或者群胚(groupoid)来描述, 非对称则用格(lattice)或者偏序集(poset)来描述. 在广义minor理论中, 我则用更加一般的无环范畴(acyclic category)来刻画小范畴的整体定向性. 更加有趣的是, 无环范畴自然地有一个莫尔斯理论, 或者说范畴化莫尔斯理论的自然框架就是无环范畴, 这也就意味着 广义minor理论背后还有一个范畴的莫尔斯理论, 它可以更好地提取小范畴地非对称信息, 正如莫尔斯理论可以提取流形地同伦信息一样.
读者如果对数学物理比较熟悉, 很容易感受到局部对称性和整体定向性在物理中的意义.众所周知, quiver gauge理论背后就是quiver的几何表示论. 再结合威腾用超对称量子力学解释莫尔斯理论的工作, 很容易想通我的广义minor理论其实描述的是规范理论中的真空的相变规律和相图结构, 是对超对称规范理论的真空结构(BPS代数)的范畴化描述. 不难想象, 它和组合霍奇(hodge)理论有自然的联系.
好了, 就此打住, 更多有趣的想法留在后文中讨论.
想看更多文章, 欢迎关注我的公众号: 数理同源

转载本文请联系原作者获取授权,同时请注明本文来自鲁学星科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3582667-1499037.html?mobile=1
收藏

