研究背景
经典矩阵方程组

在控制理论、优化算法、图像处理、系统辨识和机器人学等领域有着广泛应用。上海大学理学院王卿文教授及其团队在Symmetry 期刊发表的这篇综述文章,对该方程组的各种求解方法进行了全面总结,内容涵盖广义逆方法、矩阵分解技术以及厄米特解、极秩解、自反解和共轭解等多种形式的解,同时介绍了针对希尔伯特空间、希尔伯特C∗-模和四元数等特定代数结构的求解方法。进一步探讨了这些解的存在条件和解析表达式和最佳逼近表达及其在彩色图像等实际问题中的应用。
研究过程与结果
文章旨在总结与该方程组相关的理论成果,并强调了其在广泛应用中的核心作用。主要讨论通解、最小二乘解和最小范数解的存在条件及相应表达式,以及用于获得特殊解 (如厄米特解、非负定解、最大和最小秩解) 的广义逆方法。此外,还将相关理论延伸至希尔伯特空间、希尔伯特C∗-模和一般环等的代数结构并探讨了相应的求解方法。之后分析了特征值分解、奇异值分解和广义奇异值分解等矩阵分解方法在求解该矩阵方程组中的有效性,以及考虑了对偶数、四元数、分裂四元数和对偶四元数等特殊代数结构中的解 (如图1所示)。最后给出了该方程组在彩色图像和视频处理中的应用实例。
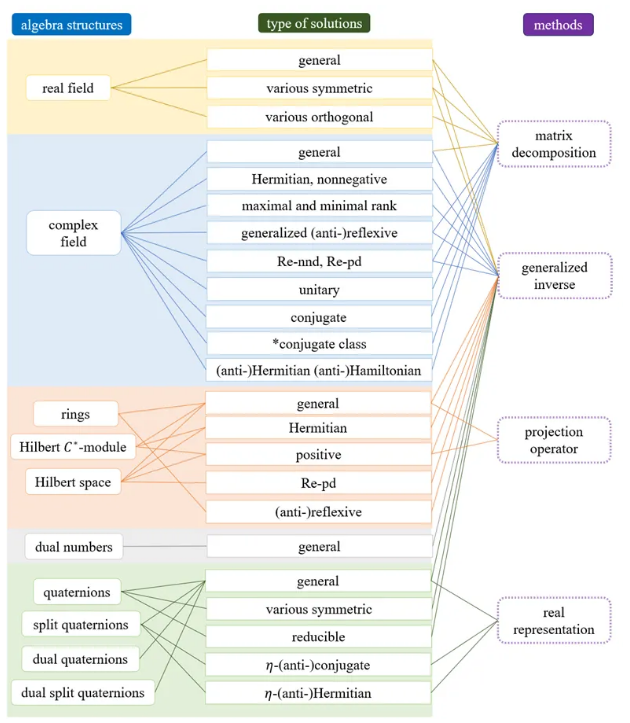
图1. 方程组AX=C和XB=D的研究框架。
研究总结与展望
鉴于广义逆和矩阵分解技术在处理大规模矩阵方程组时可能具有较高的计算复杂度,解决相关计算挑战、寻找该方程组的数值解是重要研究方向。近年来,神经网络凭借强大的学习与优化能力备受关注,利用其自适应与并行计算特性求解方程组数值解,为研究提供了新的方向与可能。张量在众多前沿领域应用广泛,然而在张量框架下对该方程组的研究尚处于起步阶段。张量的高维特性与复杂结构,为方程组研究带来全新视角,深入挖掘张量背景下方程组的性质与解法,有望开辟新的研究领域,推动多学科交叉融合。由于对偶四元数应用广泛,在对偶四元数、对偶广义交换四元数和对偶分裂四元数背景下研究该方程组的各种特殊解 (如最小范数解、厄米特解和自反解) 是值得关注的重要发展方向。这些进展有望进一步推动该方程组在控制理论、优化、图像处理、系统辨识和机器人学等领域的深入应用。
原文出自 Symmetry期刊:https://www.mdpi.com/3277854
期刊主页:https://www.mdpi.com/journal/symmetry
Symmetry 期刊介绍
主编:Sergei D. Odintsov, Institute of Space Sciences (IEEC-CSIC), Spain
期刊主题涵盖了所有科学研究中有关对称/非对称现象的理论和应用研究,主要包括数学、计算机、工程与材料、物理学、生命科学、化学等领域的最新进展。期刊已被 Scopus、SCIE (Web of Science)、CAPlus/SciFinder 等多家知名数据库收录。
2024 Impact Factor:2.2
2024 CiteScore:5.3
Time to First Decision:17.1 Days
Acceptance to Publication:2.8 Days


转载本文请联系原作者获取授权,同时请注明本文来自MDPI开放科学科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3516770-1493659.html?mobile=1
收藏

