作者介绍
纪雨露
苏州大学数学科学学院
研究方向:抽样调查。
刘洋 副教授
苏州大学数学科学学院
研究方向:抽样调查、半参数统计理论。
文章亮点介绍
由于物种个体间的异质性,负二项回归模型是拟合捕获-再捕获数据的常用模型,用于种群规模的统计推断。然而,在应用负二项模型估计散度参数时,现有的基于似然和比率回归方法通常会面临边界问题和不可辨识性问题。这会导致种群规模的点估计不稳定,并且置信区间的上限可能无界。对此,作者提出了一种惩罚经验似然法来解决这两个问题。在理论层面,作者基于该方法推导出了具有渐近正态性的最大惩罚经验似然估计以及具有渐近卡方分布的惩罚经验似然比统计量。为提高数值算法的稳定性,本文提出一种有效的期望最大化 (EM) 算法。在M步中,可以通过R基本函数glm.nb()拟合标准负二项回归模型来优化模型参数。通过模拟有限样本情况下的若干合成数据集,展现了惩罚经验似然估计存在的三个优势:边界问题完全消除,最大惩罚经验似然估计更加有效,惩罚经验似然比区间估计更加精确。这些优势在一个案例研究中得到了进一步验证,用于估计纽约州德拉姆堡军事基地内黑熊的数量。
文章介绍
1.研究背景及目的
在生态学和流行病学等诸多领域,捕获-再捕获数据广泛用于推断种群规模。捕获-再捕获方法最早应用于渔业领域,后来逐渐被广泛用于估算生态系统中物种的丰富度。在社会调查中,将每次个人前往机构的记录视为一次“捕获”,通过分析这些捕获记录,可以推断出药物或酒精成瘾者的人数。同样地,流行病学家也常利用不完整的多份患者名单来估计疾病的患病率。
传统上,泊松回归模型常被用于捕获-再捕获数据的建模。然而,相关研究表明,当捕获次数存在过度离散现象时,泊松回归模型的表现不佳。在捕获-再捕获实验中,过度离散往往源于个体间的异质性。如果模型忽略了这种异质性和过度离散,可能会导致对种群规模的低估,进而影响统计推断的准确性,甚至导致错误的解释。在这种背景下,已有文献指出,负二项回归模型可能更为适合。然而,在负二项回归模型框架下的现有方法面临诸多挑战,主要包括两个具体问题。首先,散度参数可能存在不可识别和边界问题,导致种群规模的估计量不稳健,并伴随较大的估计误差。其次,数值算法可能不够可靠,会出现无法收敛的情形。
经验似然为解决上述两个问题提供了一种可行的替代方案。Liu et al. (2017) 首次研究了捕获-再捕获研究中种群规模的半参数经验似然推断方法,Liu et al. (2018,2021,2022,2024) 将其扩展到连续时间情形、一膨胀以及协变量缺失的情况。数值实验表明,基于半参数经验似然的方法通常优于基于条件似然的方法。然而,本文的模拟研究显示,在负二项回归模型下,最大经验似然估计和区间估计仍存在边界问题。为此,本文提出使用惩罚经验似然方法来优化种群规模的估计。
2.模型及结果分析
假设物种规模为N,捕获-再捕获数据包含n个不同的个体,第i个个体被捕yi次,其协变量为xi。本文首先建立了负二项回归模型下的半参数经验似然:
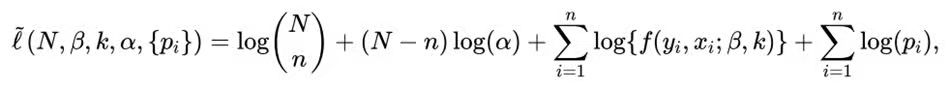
其中pi表示协变量分布在xi处的权重,α表示某个体没有被捕获的概率。f(y,x;β,k)表示负二项回归模型对应的概率质量函数:
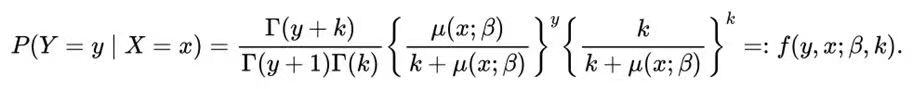
当捕获次数过度离散时,作者的模拟发现最大经验似然估计也可能遭遇边界问题。这一问题可能是由于关于种群规模的信息有限,导致经验剖面对数似然函数难以区分不同的种群规模值。为了解决这一问题,作者通过加入适当的惩罚项来修正似然函数。从贝叶斯的角度来看,在对数似然函数中加入惩罚项等同于为总体大小施加一个半正态的混合先验fp(N)=-C(N-v)2 I(N>v),其中v是N的下界,C是一个调优参数,I(∙)是示性函数。相应地,惩罚经验对数似然函数为:
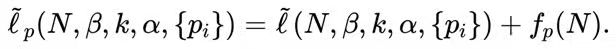
更进一步地,作者从理论层面证明了最大惩罚经验似然估计量的渐近正态性和似然比统计量渐近地服从卡方分布,这有助于构建总体规模的区间估计。
为了验证惩罚经验似然估计在真实数据集中的有效性,本文分析了一个真实的捕获-再捕获数据集。在负二项回归模型的框架下,分别应用带惩罚项和无惩罚项的最大经验似然方法,发现两种方法的点估计相同 (72,标准误差:8.9),均显著高于泊松回归模型下的估计值 (52);前者更接近比率回归估计值 (74),且标准误小于比率回归估计的标准误差 (10.2)。带惩罚项和无惩罚项的经验似然比区间估计分别为[52,201]和[52,1343]。这一差异可以通过比较带惩罚项和无惩罚项的剖面对数似然比函数 (见图1) 得到解释。图1结果显示,当实际种群规模N小于100时,这两个似然比函数几乎重合;但当N大于100时,无惩罚项的对数似然比函数随着N的增加逐渐趋于平坦,而带惩罚项的对数似然比函数则随着N的增大迅速上升,从而提高了置信区间的精度。这表明,惩罚经验似然方法能够有效缓解由过度离散化引起的边界问题。
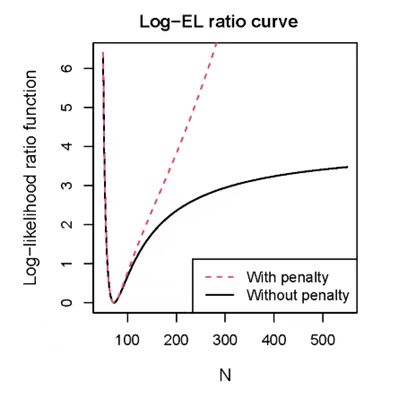
图1. 剖面对数似然比函数。
3.讨论与总结
负二项回归模型广泛用于处理捕获-再捕获数据中的异质性和离散性问题。然而,拟合该模型时,常会出现离散参数的识别和边界问题,进而导致种群规模估计值无界。为了解决这一问题,本文提出添加适当的惩罚项来减少较大种群规模时的经验对数似然函数,这等价于对种群规模施加半正态先验。这一惩罚技术能够提高最大经验似然估计的稳健性,确保生成有界区间估计。因此惩罚经验似然方法是本文的一个重要贡献。此外,本文还引入了一种高效的EM算法来最大化惩罚经验似然函数。与传统的牛顿型优化方法不同,EM算法保证了数值过程的局部收敛性,并提供了稳定的种群规模估计。相比无惩罚项的估计,所提出的最大惩罚经验似然估计更加稳健,且惩罚经验似然比区间估计更加精确。
原文出自 Mathematics 期刊:https://www.mdpi.com/2227-7390/12/17/2674
期刊主页:https://www.mdpi.com/journal/mathematics
Mathematics 期刊介绍
主编:Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK
期刊主题涵盖纯数学和应用数学所有领域,重点发表代数、几何和拓扑、函数插值、差分和微分方程、计算和应用数学、概率与统计、数学物理、动力系统、工程数学、数学和计算机科学、数学生物学、网络科学、金融数学、以及模糊集、系统和决策等相关领域的文章。现已被SCIE (Web of Science)、Scopus等重要数据库收录,JCR Category Rank: 21/489 (Q1)。
2023 Impact Factor:2.3
2023 CiteScore:4.0
Time to First Decision:17.1 Days
Acceptance to Publication:2.6 Days


转载本文请联系原作者获取授权,同时请注明本文来自MDPI开放科学科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3516770-1466402.html?mobile=1
收藏

