文章导读
元启发式算法 (Metaheuristic algorithms) 是一类能够有效解决复杂的优化问题的算法,通过搜索和优化的方法来找到问题的最佳或近最佳解。其核心思想是通过在问题空间中搜索,来逐步逼近问题的最优解,主要优点是可以处理复杂的、非线性的问题,不仅概念简单、易于实现,并且不依赖于问题类型。这些优点使得元启发式算法在工程和科学领域渐渐被引入来解决现实生活中的复杂优化问题。
2023年,来自赫拉德茨-克拉洛韦大学的Pavel Trojovský 和Mohammad Dehghani博士提出了一种新颖的元启发算法——减法平均优化器 (Subtraction-Average-Based Optimizer,SABO),该算法显著优点是具有寻优能力强,收敛速度快等,有效地解决了优化问题。
研究内容
1.灵感来源
SABO的设计基本灵感来自数学概念,如平均值、搜索代理的位置差异以及目标函数两个值之差的符号。使用所有搜索代理 (即第t次迭代的种群成员) 的算术平均位置,而不是仅仅使用最佳或最差搜索代理的位置来更新所有搜索代理的位置,这个想法并不新鲜,但SABO的算术平均值计算概念却是独一无二。
首先粒子初始化公式与大多数算法一致,在上下限值的范围内使用rand函数生成随机粒子:
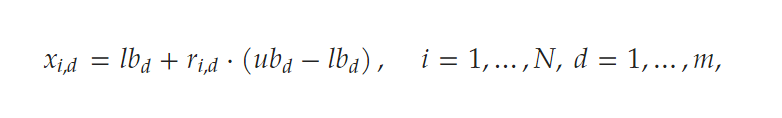
而SABO数学模型引入了一个新的计算概念,“-v”,称为搜索代理B与搜索代理a的v-减法,定义如下:
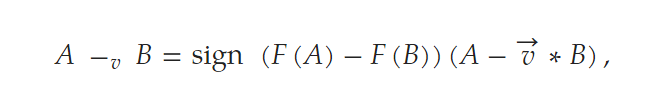
其中v是一个[1, 2]生成的随机数, F(A)和F(B)分别是搜索代理A和B的目标函数的值,sign是signum函数。在 SABO 算法中,任何搜索代理 Xi 在搜索空间中的位移都是通过每个搜索代理 Xj (j = 1, 2, . . . , N) 从搜索代理 Xi 中减去 v− 的算术平均值来计算的。因此,每个搜索代理的新位置都是使用以下公式来计算:
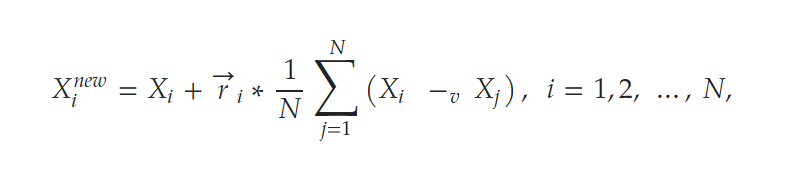
N是粒子的总数,ri 是一个服从正态分布的随机值。Xnew 其中是第i个搜索代理X的新位置,N为个体的总数,F为维数为m的向量,其中各分量的值在区间[0,1]内呈正态分布。如果新位置适应度值提高,则接受新位置,否则保持不变。最后粒子替换使用以下公式进行:
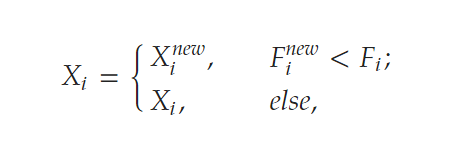
其中 Fi和 Finew 分别是搜索代理 Xi 和 Xinew 的目标函数值。SABO的数学模型图如下:
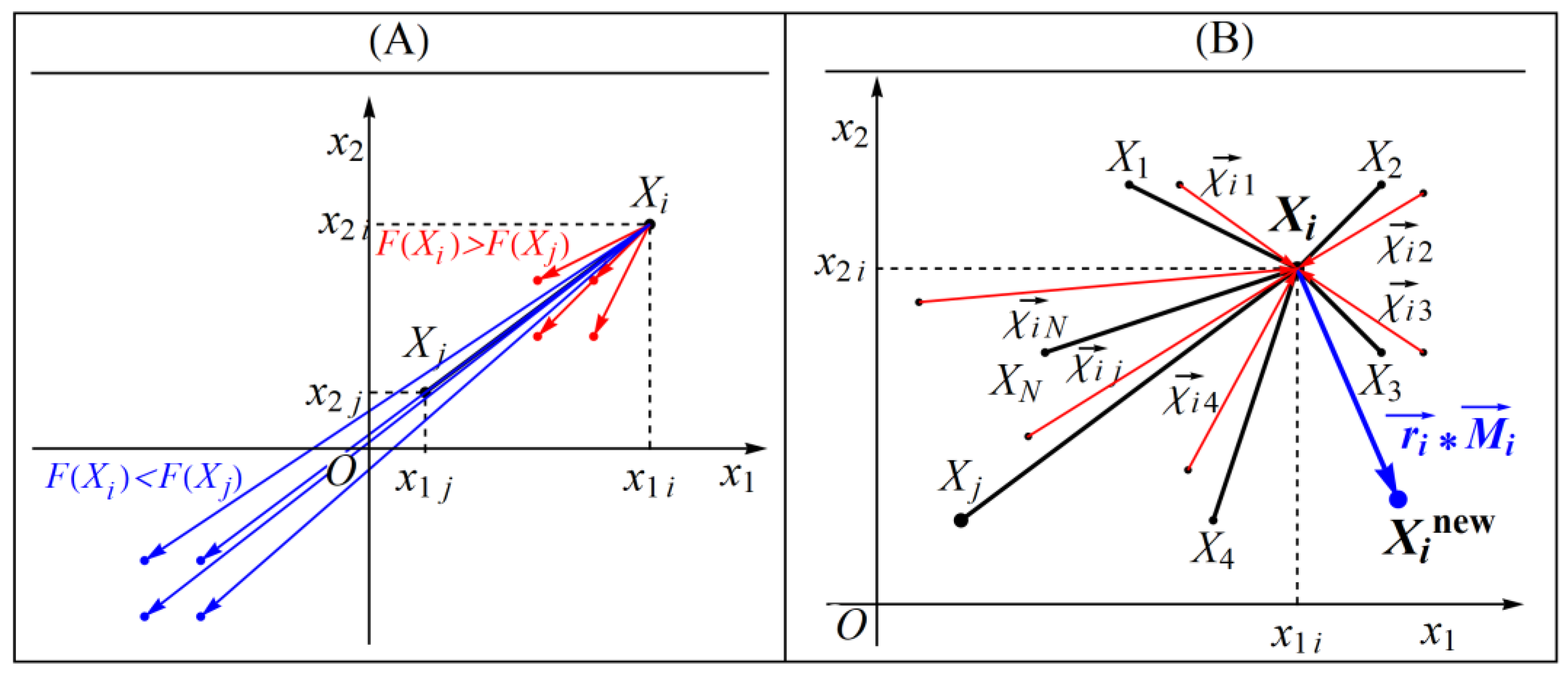
数学模型图
2.SABO的算法流程
在更新所有搜索代理后,算法的第一次迭代完成。然后,基于对搜索代理和目标函数的位置进行评估的新值,算法进入下一次迭代。在每次迭代中,最佳搜索代理都会被存储为迄今为止的最佳候选解决方案,更新搜索代理的过程一直持续到算法的最后一次迭代。最后,在算法迭代过程中存储的最佳候选解决方案将作为问题的解决方案呈现,算法流程如图所示。
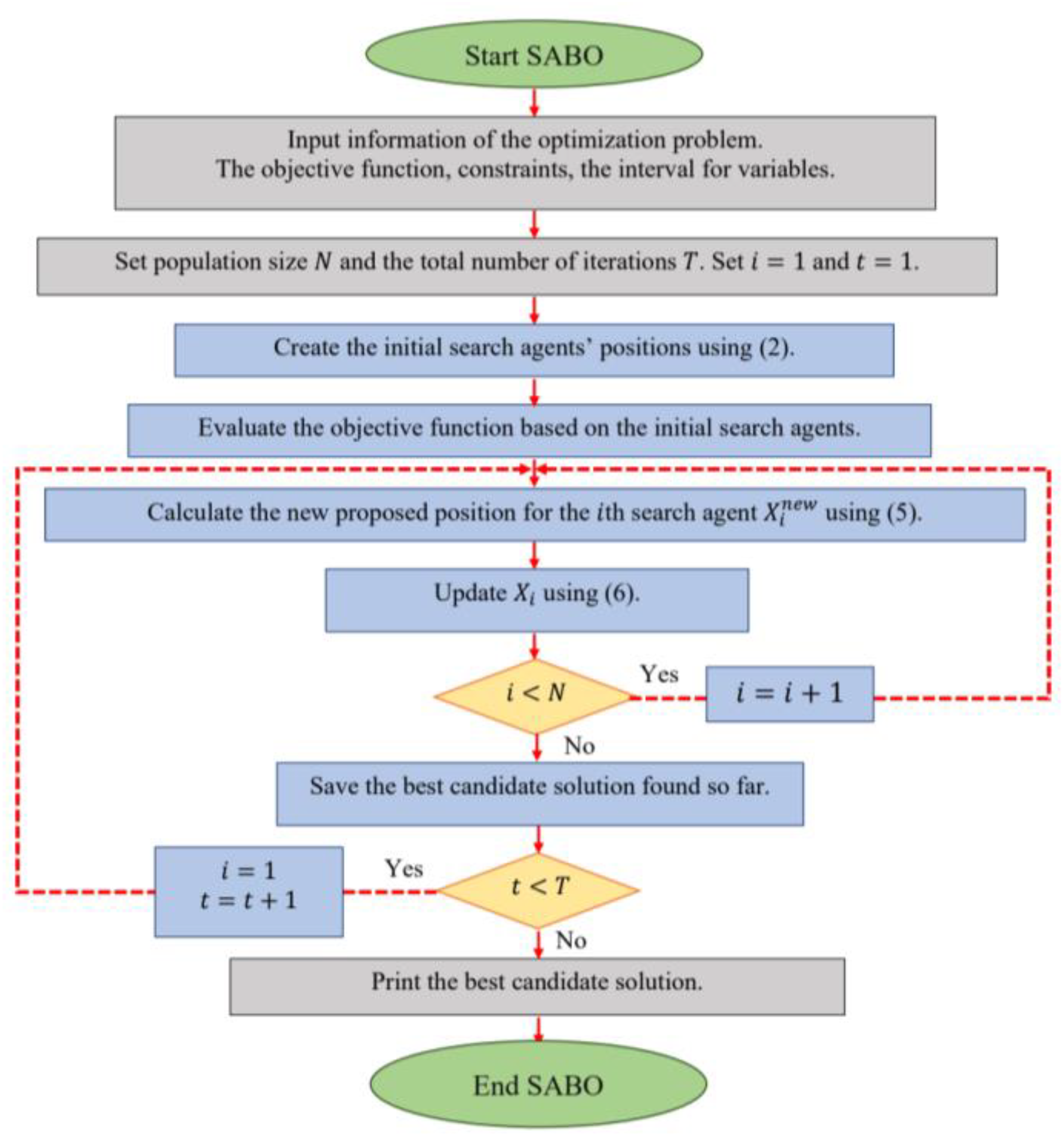
图为算法流程
3.性能测试
所提出的SABO方法的性能针对52个标准基准函数的优化进行了测试,包括单峰、高维多峰和固定维多峰类型,以及CEC 2017测试套件,此外,针对四个工程设计问题实施了所提出的方法,以评估SABO在处理实际应用程序优化任务时的效果。
实验结论
SABO的结果与12种著名的元启发式算法的性能进行了比较,仿真结果分析表明,所提出的SABO方法为大多数基准函数提供了优异的结果,并且它提供了比其竞争对手算法更具竞争力和出色的性能。
在算法中,收敛性是评价算法性能的重要指标之一。算法的收敛速度越快,其执行效率越高。以下展示SABO在处理四个实际工程设计问题的程序优化任务时的收敛曲线,来表现SABO在实际应用中处理这些优化任务的能力。
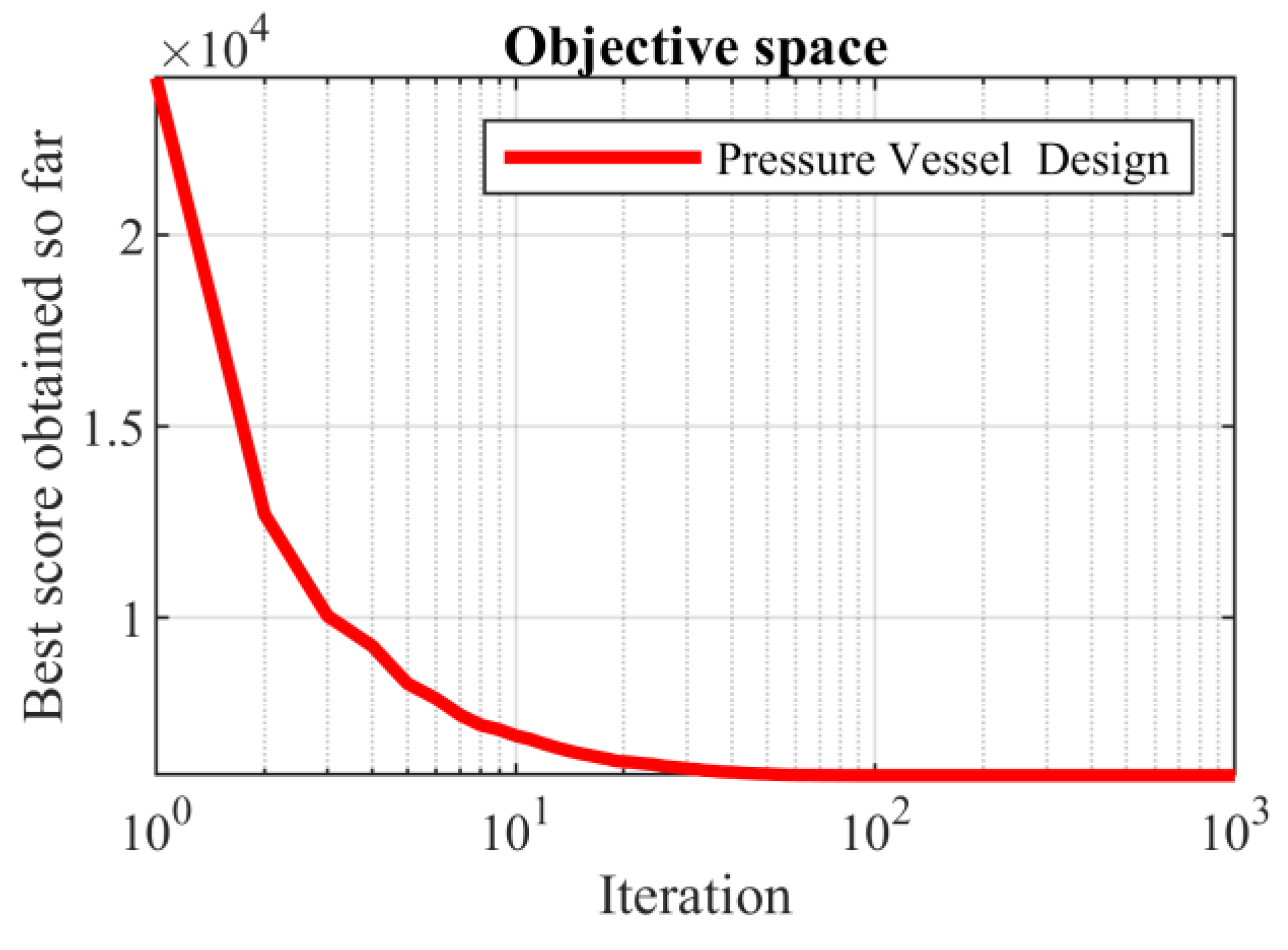
图为压力容器设计优化过程
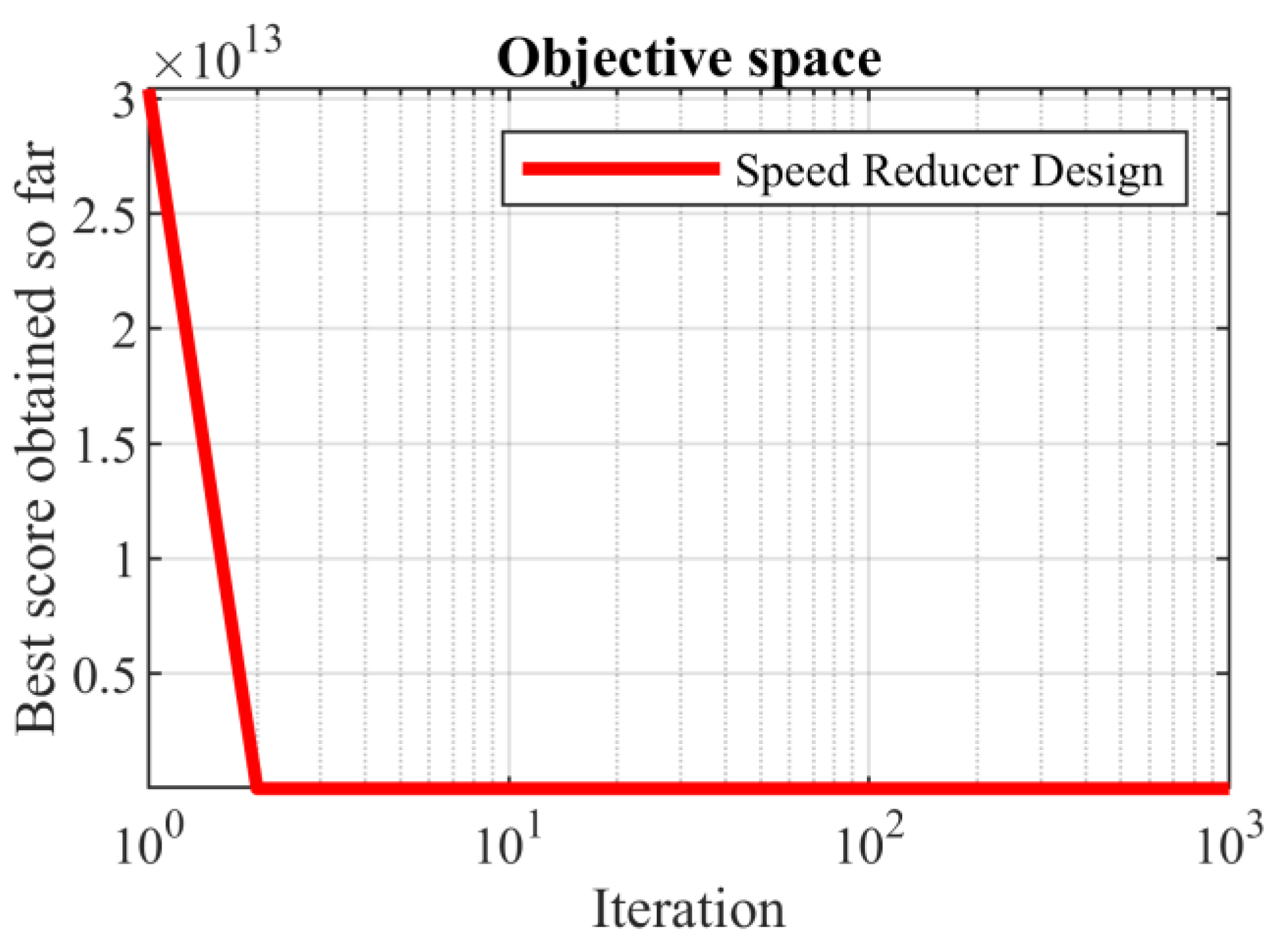
图为减速器设计问题实现最优解时
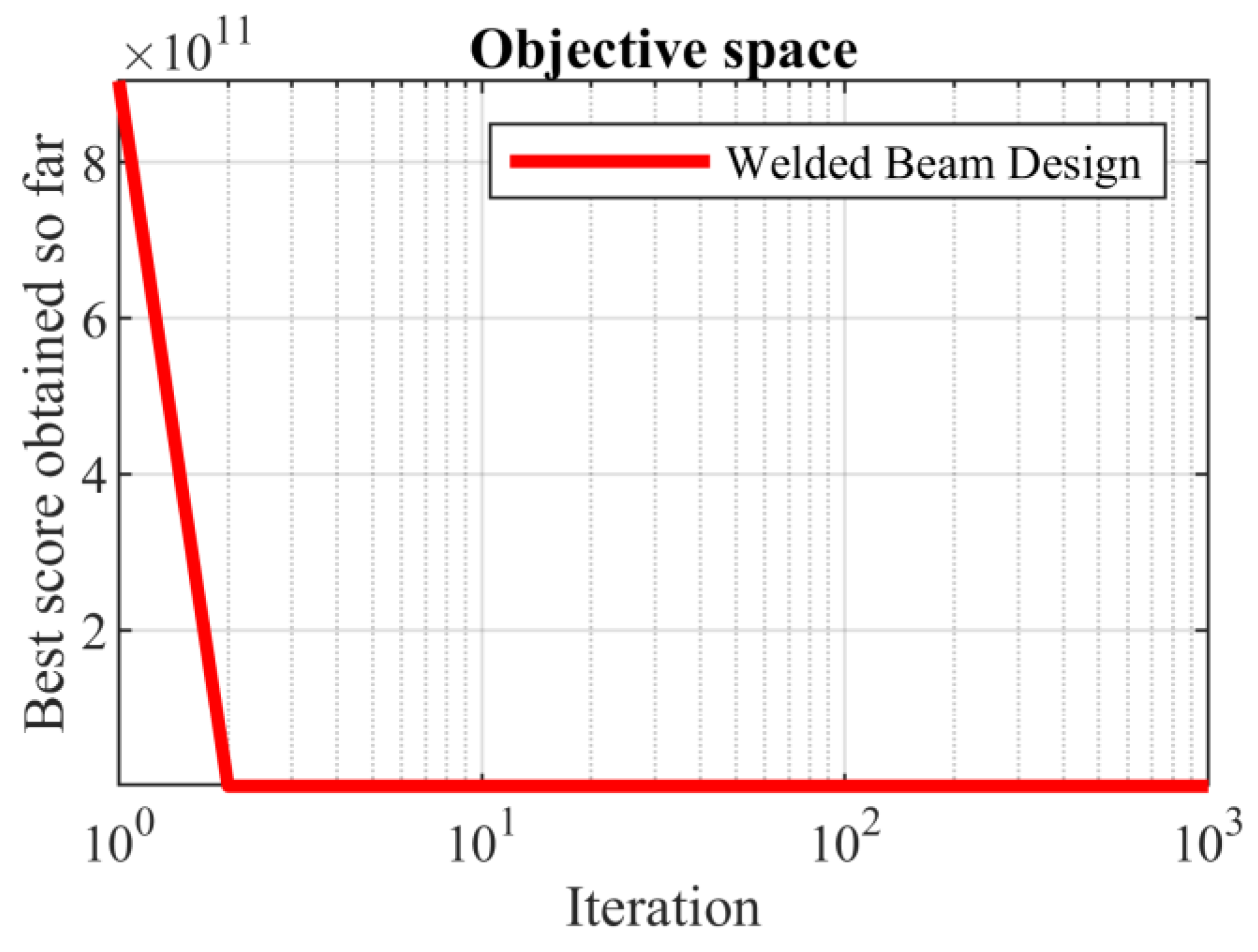
图为焊接梁设计问题提供解决方案时
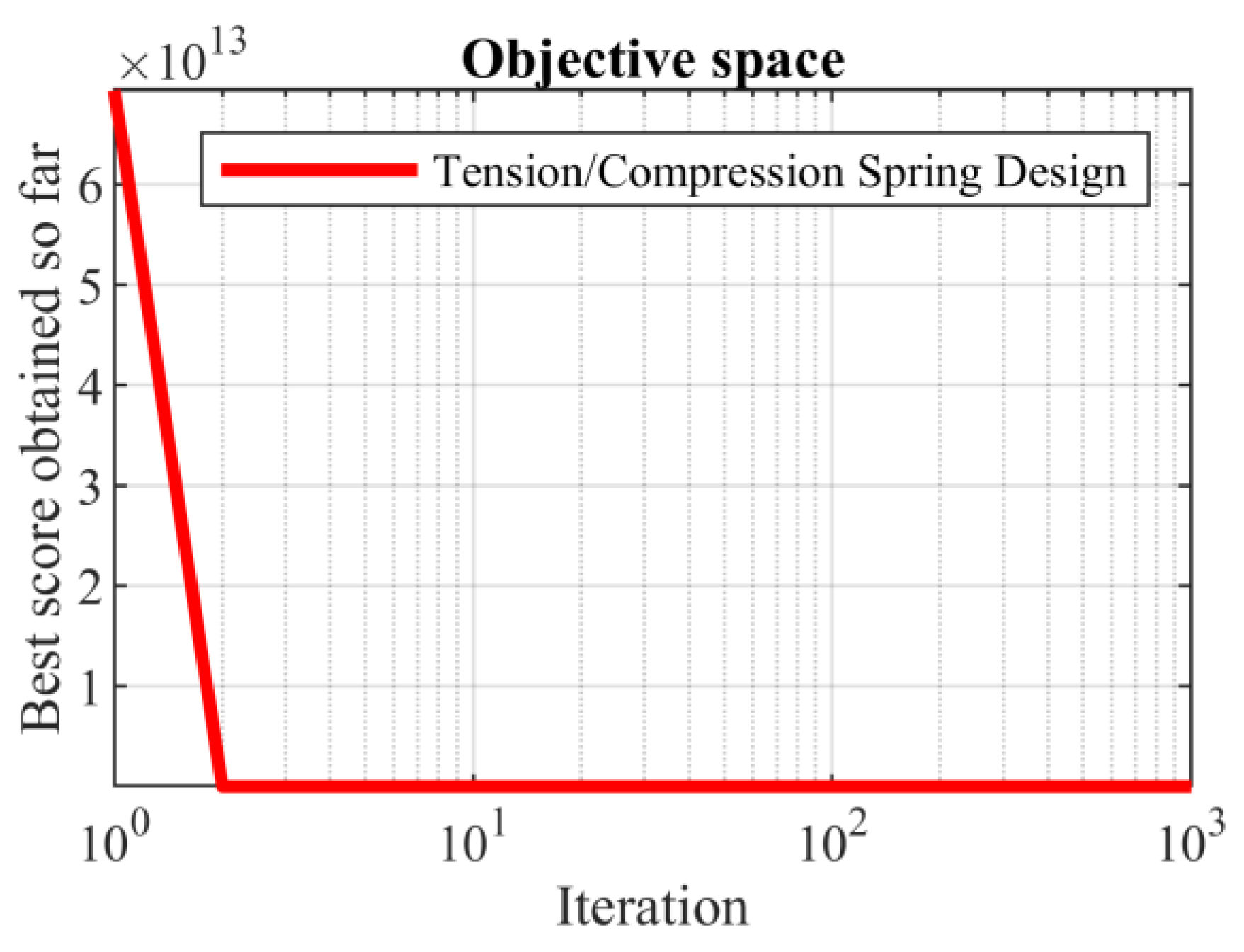
图为达到拉伸/压缩弹簧问题最优设计
原文出自 Biomimetics 期刊:https://www.mdpi.com/journal/biomimetics
阅读原文:https://www.mdpi.com/2235102
Biomimetics 期刊介绍
主编:Stanislav N. Gorb, Kiel University, Germany
期刊致力于研究生物体的最基本方面及其特性向人类应用的转移。期刊旨在为材料科学、机械工程、纳米技术和生物医学领域的研究人员和专业人士提供一个平台,通过在工程系统、技术和生物医学中利用生物启发的设计,开发实现可持续创新的解决方案。
2023 Impact Factor:3.4
2023 CiteScore:3.5
Time to First Decision:20.3 Days
Acceptance to Publication:2.9 Days


转载本文请联系原作者获取授权,同时请注明本文来自MDPI开放科学科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3516770-1445795.html?mobile=1
收藏

