自洽性是数学理论的核心特征。自洽性要求数学理论能够自圆其说，在其理论内部始终要保持概念的一致性和无矛盾性。
如果一个数学理论中出现一个整数N既是“偶数”也是“奇数”的矛盾描述，则该理论不能自洽，会不攻自破，立即从教科书中淘汰消失。
在《随机过程》教科书中，对于“一个粒子”的空间位置随时间t的变化过程，随机过程定义将其称为随机过程的“一个物理实现”或 “样本函数”，定义为固定ω时的随机过程X(ω,t)，用小写x(t)表示。对于“所有粒子”在t时刻的空间位置，随机过程定义将其称为“随机变量”，定义为固定t时的随机过程X(ω,t)，用大写X(t)表示。
注意：样本函数x(t)是时间t的函数，随机变量X(t)虽然使用了时间函数符号，但它不是时间t的函数，而是样本点ω的函数。
令人不可思议的是，《随机过程》布朗运动定义竟然没有保持与随机过程定义概念的一致性，却用“随机变量”及其数字特征来描述随机过程的“一个物理实现”和“一个粒子”的空间位置随时间t的变化过程，与随机过程定义产生矛盾，不能自洽（表1）。
表1 随机过程定义与布朗运动定义对比
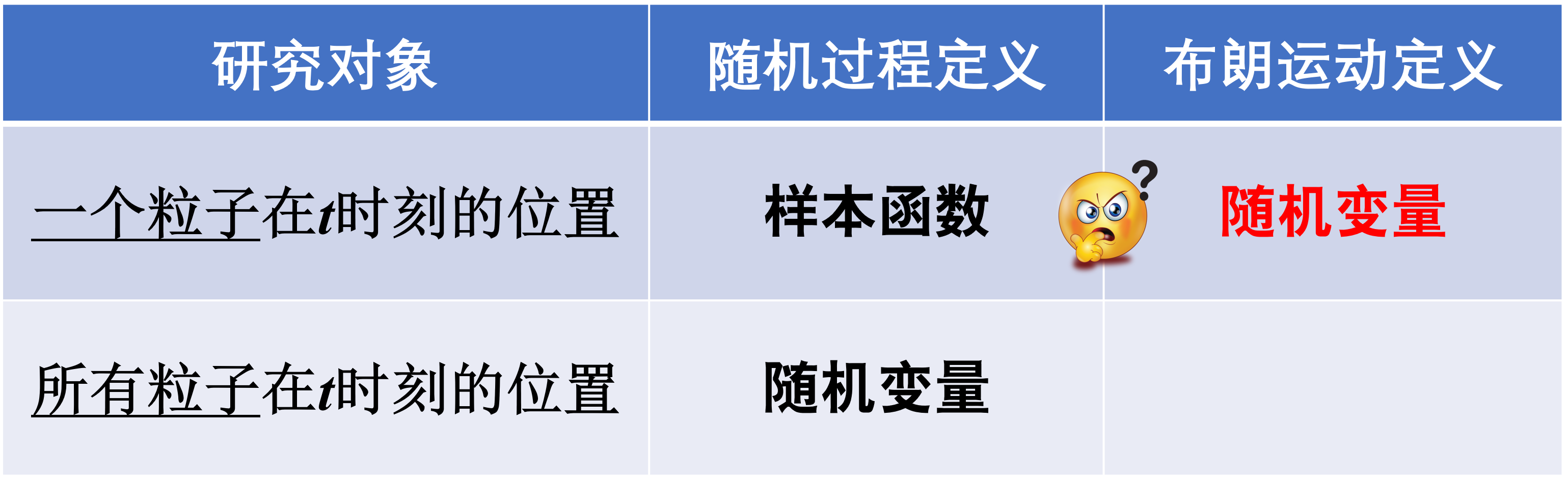
《随机过程》布朗运动定义与随机过程定义不能自洽的原因在于：布朗运动定义违反了逻辑推理基本规则——同一律，没有保持与随机过程定义的概念同一， 用“随机变量”来描述“一个粒子”在t时刻的空间位置，因而产生了“偷换概念”逻辑错误，导致布朗运动定义与随机过程定义不能自洽。
《随机过程》布朗运动定义“偷换概念”的逻辑错误，导致《随机过程》对布朗运动位移和瞬时速度的描述与自然科学、工程技术和社会科学大量的观察实验结果不符，无法正确描述实际的布朗运动现象及规律。
《随机信号分析》保持了与随机过程定义的概念同一， 用“样本函数”来描述“一个粒子”在t时刻的空间位置，因此对布朗运动位移和瞬时速度的描述与客观事实相符，可正确描述实际布朗运动现象及规律。
转载本文请联系原作者获取授权，同时请注明本文来自高宏科学网博客。
链接地址：https://wap.sciencenet.cn/blog-3418723-1489978.html?mobile=1
收藏
