在“工程师与数学家的布朗运动理论对比”一文中，介绍了工程师建立的布朗运动理论可正确描述实际的布朗运动现象及规律，并在航空、航天、航海和军事等领域获得了广泛应用；反而是数学家建立的布朗运动理论无法正确描述实际的布朗运动现象及规律，在金融市场的应用导致B-S期权定价公式成为造成1987、1997和2007年三次重大金融危机的罪魁祸首。

主要原因在于：工程师有时域分析、频域分析、系统分析和实验分析这四种现代分析工具，而数学家仅仅掌握概率分析这一种古老的静态分析工具，又没有实验分析工具对研究对象进行实验观察，或对研究成果进行实验检验，因此，工程师的4种随机过程分析工具降维碾压数学家的概率分析，形成了4维比0.5维的巨大研究优势，特别是具有“上帝视角”的频域分析方法很容易发现数学家在时域无法看到的随机过程动态特征及规律。

图1 数学家和工程师的随机过程分析工具

1、时域分析

对随机过程进行观察，往往会得到一些随时间变化的曲线，工程师称之为随机信号，并用函数符号x(t)来代表（尽管不能给出具体的方程式）。

数学家会用“概率分析”方法计算出x(t)取正值的概率p和取负值的概率q。

工程师则会用“时域分析”方法计算出x(t)的均值、方差和自相关函数。

均值μ描述了x(t)中直流分量的大小，方差σ²则描述了x(t)中交流分量的强度（平均功率），直流分量和交流分量均可用仪器直接测量，自相关函数描述了x(t)在不同时刻的相关程度。

均值μ与概率p和q具有如下的数量关系：

μ=p-q

从上式可以看出，概率p和q反映的是随机信号x(t)中的确定性成分——直流分量，或p-q的物理意义就是随机信号x(t)中的直流分量。

由于直流分量是基本物理量，并具有明确直观的物理意义和测量手段，因此工程师通常用均值μ或直流分量来描述x(t)中的确定性，而不使用概念抽象的概率p和q来描述x(t)中的确定性。

2、频域分析

随机过程x(t)在时域无法用确定性的数学解析式来描述，但是在频域却可用确定性的数学解析式表示。例如，布朗运动x(t)在频域的功率谱密度P_x(ω)可表示为

式中N₀为布朗运动瞬时速度的平均功率。

从布朗运动的功率谱可以看出，布朗运动x(t)是能量集中在低频段的红噪声（Red Noise），x(t)是分形指数γ= 2或Husrt指数H=0.5的1/f分形信号，在时间尺度上具有局部自相似性和长程相关性，在宏观尺度上存在可以识别和利用的规律，具有可预测性。

频域可以提供比时域更直观、更丰富的信息，从而能深刻地揭示出随机过程的特征及规律，看到时域角度看不到的问题，发现隐藏在随机现象下的确定性特征及规律，因此，频域也被专业学者们称为上帝的视角（图2）。

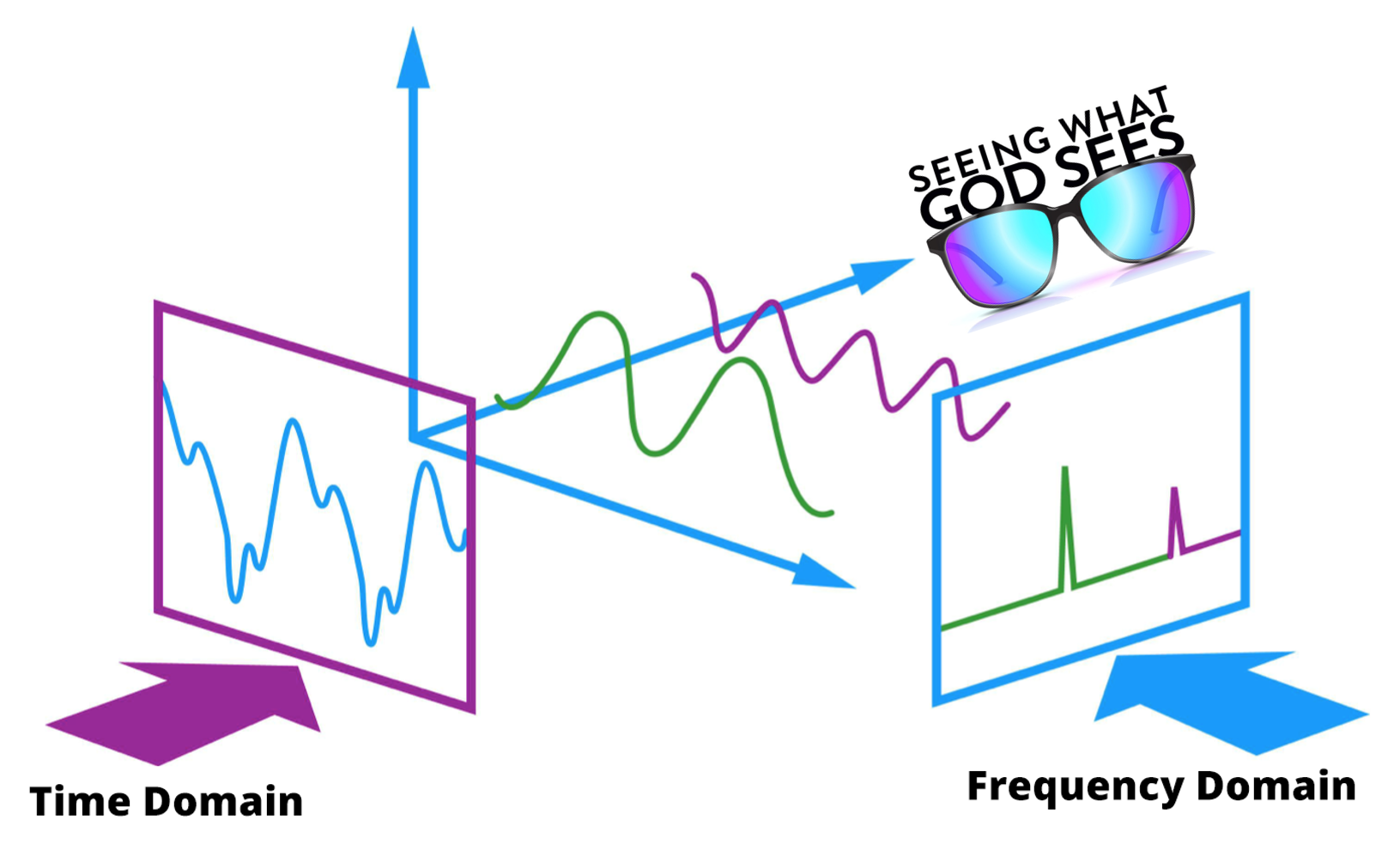
图2 频域分析（上帝视角）

3、系统分析

“系统”是指能对各种“输入信号”按一定规则进行加工、运算和变换，并产生相应“输出信号”的装置或算法。

从工程师的角度看，任何随机过程x(t)都可看作是白噪声n(t)激励系统时所产生的输出（图3）。

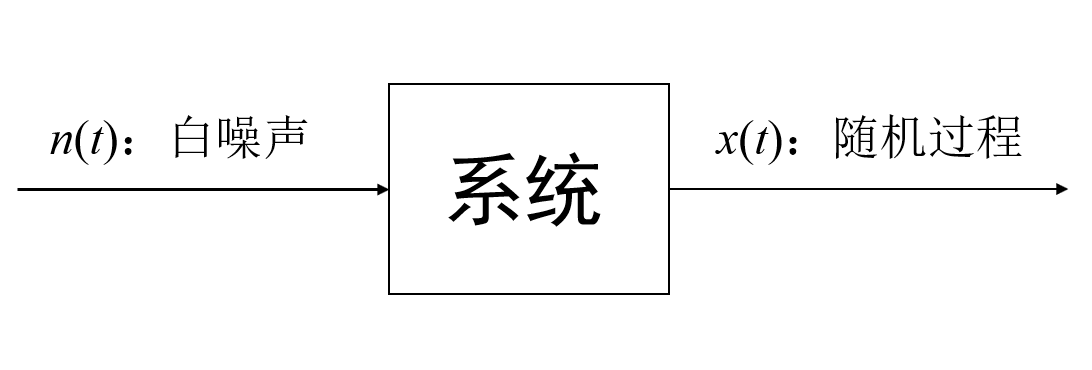
图3 随机过程系统模型

白噪声n(t)的功率谱密度为常数，因此，随机过程x(t)的功率谱密度完全由系统传递函数（Transfer Function）决定，工程师把对随机过程的研究转变为对确定性系统传递函数的研究，利用已经非常成熟的各种确定性系统传递函数研究成果，可方便地分析随机过程x(t)。

例如，布朗运动x(t)是白噪声n(t)激励积分系统时所产生的输出，根据积分系统的传递函数，立即可得布朗运动x(t)的功率谱密度为

式中N₀为白噪声n(t)的平均功率。

4、实验分析

实验分析方法是近代自然科学的精髓，它是获取科学事实和感性认识的基本途径，也是形成、发展和检验科学理论的实践基础，许多科学重大发现也是通过实验方法直接获得的。

实验分析方法对工程师尤其重要，可以验证理论、模型及方法是否与客观事实相符，以及实际问题是否最终得到有效解决。

数学家从不使用实验分析方法来观察实际随机现象，也从不使用实验分析方法来检验《随机过程》理论否与客观事实相符，因而100多年来，始终无法发现《随机过程》理论不能正确描述随机过程现象及规律的问题。

诺贝尔物理学奖得主、美籍物理学家理查德·费曼（Richard Feynman）1965年在康奈尔大学举行的“数学与物理学的关系”信使系列讲座中，谈论了对数学家的看法：“数学家们只注重处理推理的结构，而非推理的内容，就像他们自己所说的，他们不需要知道自己在说什么，也不必知道自己说的是否正确。”

5、结论

从工程师的角度看，数学家的“概率分析”只能看到随机过程在时域的局部静态特征，而看不到随机过程的其它方面及动态发展变化的全过程。因此，数学家对随机过程的研究仍处于盲人摸象的阶段，而工程师则拥有数学家无法企及的研究优势，可从多个维度和“上帝视角”全面研究整个随机过程的动态发展变化全过程。

数学家们深陷“概率分析”认知壁垒而不自知。当工程师指出《随机过程》理论与客观事实不符的问题时，数学家会居高临下地说：你不懂概率，建议去看《概率论》，工程师只能苦笑，脑子里会蹦出庄子的一句话：井蛙不可语海。

参考：

[1] 工程师与数学家的布朗运动理论对比

https://blog.sciencenet.cn/blog-3418723-1458528.html   

[2]教科书中两种对立冲突的布朗运动理论及实际应用效果

https://blog.sciencenet.cn/blog-3418723-1458326.html   

转载本文请联系原作者获取授权，同时请注明本文来自高宏科学网博客。

链接地址：https://wap.sciencenet.cn/blog-3418723-1459016.html?mobile=1

收藏

分享