引用本文

齐佳鑫, 孟桂芝. 基于强化学习的控制方向未知非线性系统的最优输出调节. 自动化学报, 2025, 51(7): 1688−1702 doi: 10.16383/j.aas.c240323

Qi Jia-Xin, Meng Gui-Zhi. Optimal output regulation for nonlinear systems with unknown control direction based on reinforcement learning. Acta Automatica Sinica, 2025, 51(7): 1688−1702 doi: 10.16383/j.aas.c240323

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240323

关键词

控制方向未知，最优输出调节，强化学习，有限时间 

摘要

针对一类由线性中性稳定的外系统驱动的带有未知非线性函数和外界扰动的控制方向未知非线性系统, 研究基于强化学习的有限时间最优输出调节问题. 首先, 根据调节器方程可解条件和坐标变换, 将控制方向未知非线性系统的输出调节问题转化为控制增益已知的增广系统的镇定问题. 接着利用径向基神经网络去逼近未知非线性函数, 设计具有内模的高增益神经网络自适应观测器去估计不可测的状态, 引入Nussbaum函数来解决控制方向未知问题. 然后, 设计基于神经网络观测器和Nussbaum函数的新的自适应内模, 提出与内模相关的代价函数, 并且在反步法中运用基于强化学习中的执行−评价网络的近似最优算法, 保证了虚拟控制器为最优, 同时结合动态面技术避免反步法中的“复杂度爆炸”问题. 最后, 通过所设计的最优自适应有限时间输出反馈控制器, 不仅使得提出的价值函数达到最优, 而且还确保了闭环系统的信号半全局实际有限时间稳定, 且跟踪误差在期望的任意精度内. 数值仿真验证了所提方法的有效性.

文章导读

输出调节是控制理论领域中的热点问题, 在生活中有广泛的应用, 例如机器人控制[1]、电压调节[2]等. 输出调节的目标是对给定的被控对象设计反馈控制律, 在确保闭环系统稳定的前提下, 使被控系统的输出渐近跟踪一类参考信号或抑制一类干扰信号. 这里参考信号与干扰信号称为外信号, 它是由一个被称为外系统的自治微分方程生成的. 对于线性输出调节, 内模原理[4]的出现使该问题得到解决. 对于非线性输出调节, 文献[5]提出一种解决问题的通用框架, 即将输出调节问题转化为镇定问题, 该框架极大地促进了非线性输出调节的研究.

在工程实践中, 系统不可避免地面临诸如测量误差、外部扰动和控制方向未知等不确定性因素. 对于不确定的下三角严格反馈非线性系统, 反步法[6]是一个行之有效的方法. 但是应用反步法会产生反复求导、导致“复杂度爆炸”现象, 因此引入动态面技术[7]去解决该问题. 文献[8]针对一类非线性多智能体系统, 应用动态面技术、障碍Lyapunov函数和神经网络, 引入量化器, 构建一种基于自调节有限时间预设性能函数的动态面状态约束量化控制策略. 但文献[6−8]都没有考虑控制方向未知的问题. 而对控制方向未知的问题, 文献[9]首次运用Nussbaum函数解决控制方向未知的非线性系统的镇定问题, 该技巧至今仍是解决此类问题的主流途径. 文献[10]利用Nussbaum函数、神经网络和动态面技术设计自适应神经网络动态面控制器, 解决一类控制增益未知的不确定非线性系统的输出跟踪控制问题. 但文献[9−10]针对的都是系统的镇定问题. 文献[11]采用自适应反步控制方法和Nussbaum增益技术, 解决具有高频增益信号和控制系数未知的非线性系统的输出调节问题. 文献[12]使用障碍Lyapunov函数和Nussbaum增益技术, 解决一类带有未知控制输入方向的非线性系统的约束鲁棒输出调节问题. 文献[9-12]都没有考虑有限时间控制的问题. 但在工程应用中, 往往需要在有限时间内确保系统的稳定性能, 以满足实际需求和工程标准, 有限时间稳定更具有实际意义[13−16]. 文献[17]对控制方向未知且有执行器故障的不确定非线性系统采用加功率积分器技术, 设计一种开关型自适应有限时间控制器, 确保系统可以全局有限时间镇定. 文献[18]针对控制方向未知和死区且带有未知项的严格反馈非线性系统, 结合模糊状态观测器、反步法和Nussbaum函数设计控制器, 使得系统半全局实际有限时间稳定. 需要注意的是, 文献[17−18]解决的是有限时间镇定问题. 而文献[19]针对由未知线性外系统驱动的控制方向未知的不确定严格反馈非线性系统, 将Nussbaum函数与模糊控制、反步法相结合, 解决系统的有限时间输出调节问题. 但是上述文献[9−19]均没有考虑最优控制.

在实际应用中, 如何在资源和环境条件的制约下, 实现快速跟踪和扰动抑制变得至关重要, 因此对最优控制问题的研究变得不可或缺. 最优控制的目的就是在满足一定约束条件的前提下, 寻找一个能够最大化或最小化系统性能指标的控制律, 进而达成预设的目标. 非线性系统最优控制问题的解决需要求解哈密顿−雅可比−贝尔曼(Hamilton-Jacobi-Bellman, HJB)方程. 但随着系统维数的增加, 方程不容易求解析解. 为解决上述问题, 学者们想到基于强化学习思想得到HJB方程的近似解[20−24]. 强化学习在生活中也有广泛的应用, 如自动驾驶[25]、长列车下坡[26]、障碍规避[27]等. 文献[28]介绍最优反步法的概念, 即, 在反步法的每一步骤中, 都融合强化学习中的执行−评价算法, 以实现每一步虚拟控制的最优化, 进而优化整个系统的控制性能至最佳状态. 文献[29]针对系统状态未知的带有输入约束的不确定非线性系统, 利用最优反步法解决最优跟踪控制问题. 目前, 关于非线性系统最优输出调节问题的研究比较少, 文献[30]将执行−评价算法和鲁棒重设计技术相结合, 设计约束鲁棒最优反馈状态控制器, 解决了具有不确定性约束的非线性系统的鲁棒最优输出调节问题. 但是文献[30]未考虑状态部分未知、控制方向未知和有限时间的情况.

本文的主要贡献如下: 1)针对一类由线性外系统驱动的具有控制方向未知和未知非线性函数, 且状态部分未知的非线性系统的有限时间最优输出调节问题, 利用Nussbuam函数解决控制方向未知的问题, 同时提出基于强化学习的有限时间最优自适应控制策略. 2) 由于外系统的存在和有限时间的引入, 文献[28−29]中给出的代价函数和最优价值函数表达式都将不再适用, 这也是本文的研究难点. 为解决该问题, 提出新的代价函数和新的最优价值函数表达式. 3)设计基于强化学习的高增益状态观测器和基于Nussbuam函数的新的自适应内模.

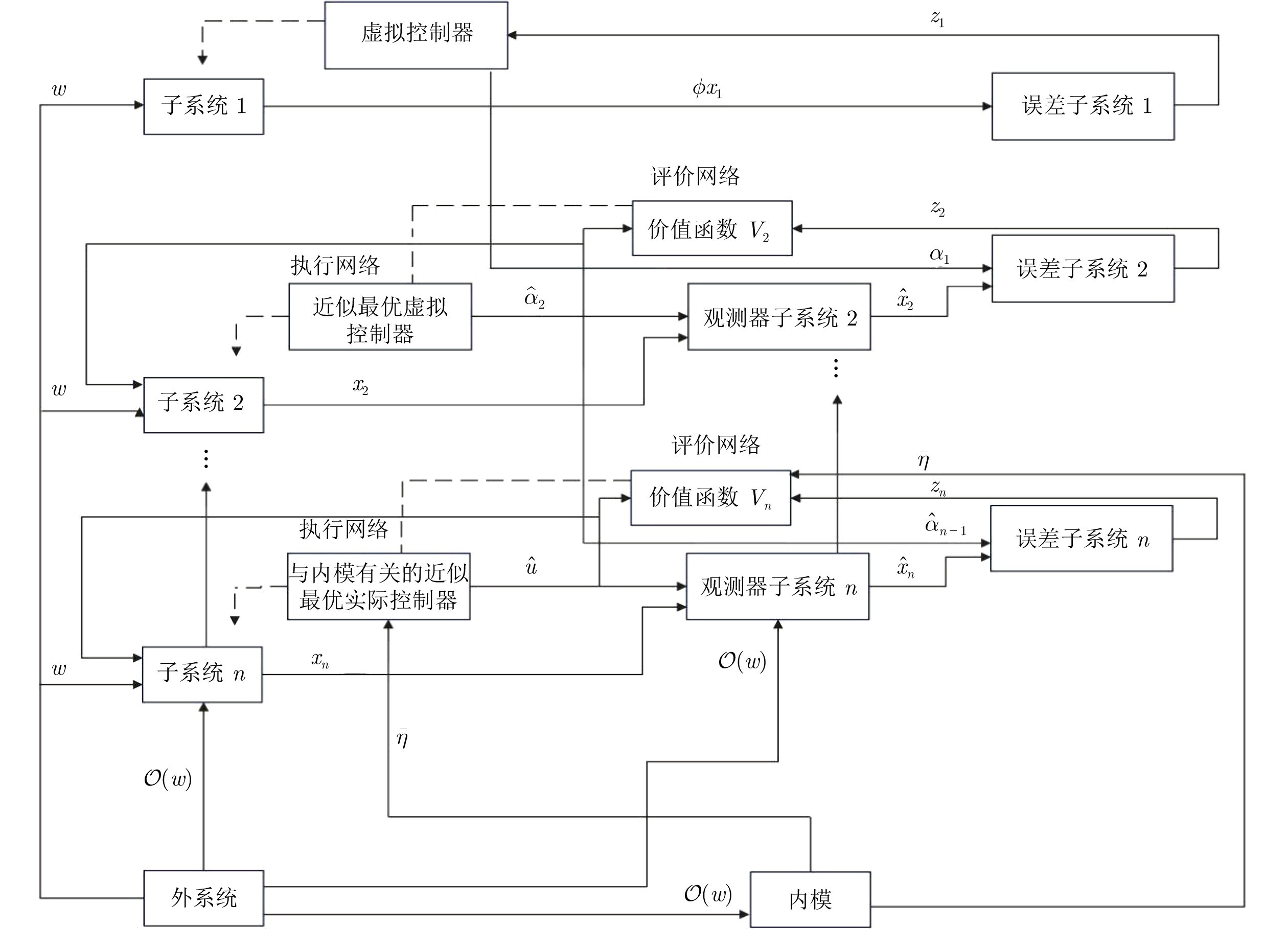
图 1  基于强化学习的最优输出调节系统结构图

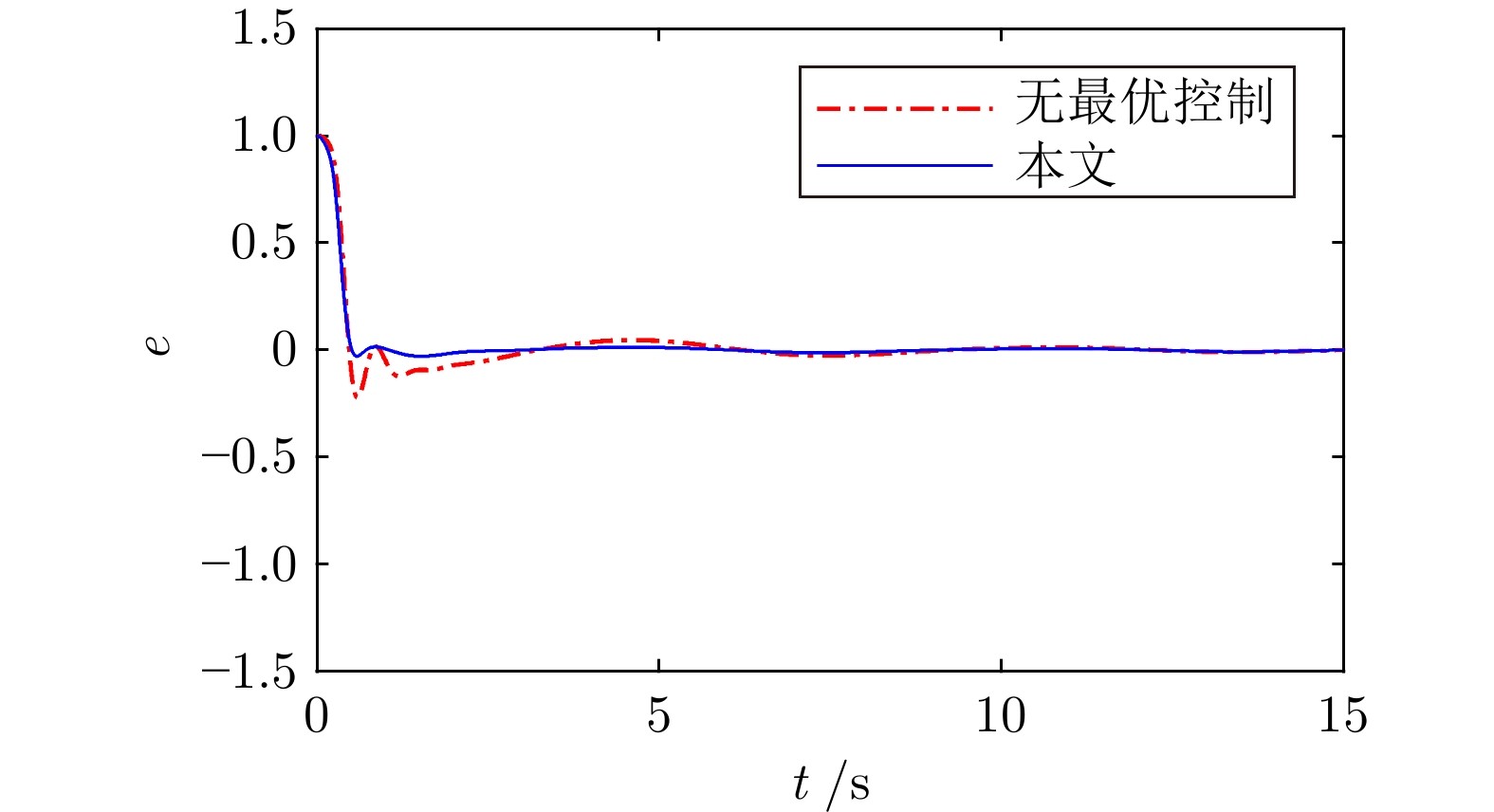
图 2  跟踪误差对比1

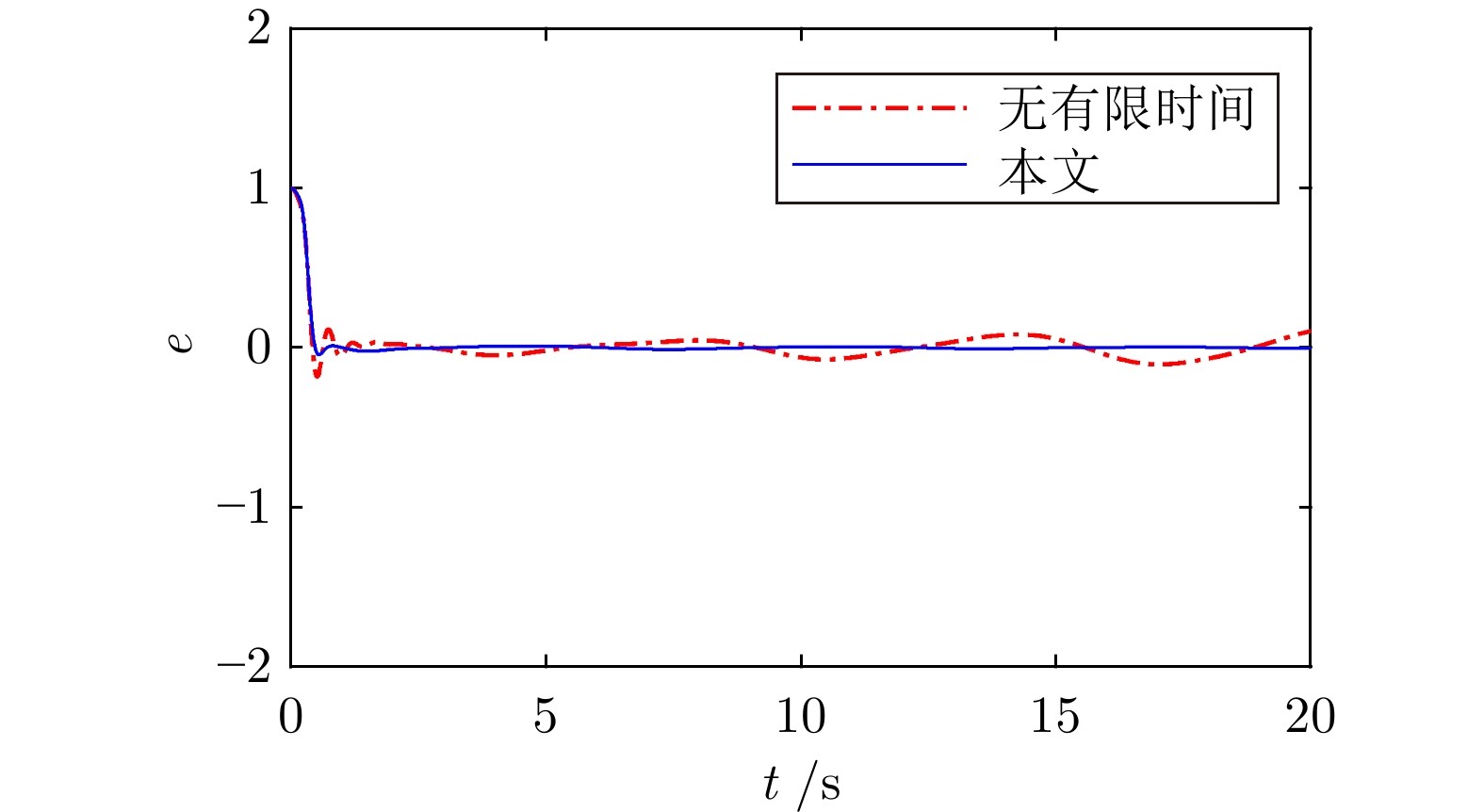
图 3  跟踪误差对比2

本文研究一类存在外系统且控制方向未知的严格反馈非线性系统的有限时间最优输出调节问题. 基于最优反步法的思想, 提出一种有限时间最优输出调节的控制策略. 首先, 利用神经网络构建高增益神经网络观测器去估计不可测的状态; 接着, 利用 Nussbaum函数去解决控制方向未知的问题; 然后, 利用最优反步法的思想, 提出与内模相关的代价函数和有限时间相关的新的最优价值函数表达式, 得到相应的有限时间最优控制器和带有误差的内模方程, 同时应用动态面技术来避免“复杂度爆炸”现象; 最后, 基于有限时间李雅普诺夫稳定性理论证明闭环系统的稳定性. 仿真结果表明了所提出的方法对于有限时间最优输出调节的有效性.

作者简介

齐佳鑫

哈尔滨理工大学理学院硕士研究生. 主要研究方向为非线性控制. E-mail: qjxin999@163.com

孟桂芝

哈尔滨理工大学理学院教授. 2013年获得哈尔滨工业大学控制科学与工程专业博士学位. 主要研究方向为非线性控制和优化, 强化学习. 本文通信作者. E-mail: menggz13@163.com