引用本文
胡光政, 朱圆恒, 赵冬斌. 两团队零和博弈下熵引导的极小极大值分解强化学习方法. 自动化学报, 2025, 51(4): 875−889 doi: 10.16383/j.aas.c240258
Hu Guang-Zheng, Zhu Yuan-Heng, Zhao Dong-Bin. Entropy-guided minimax factorization for reinforcement learning in two-team zero-sum games. Acta Automatica Sinica, 2025, 51(4): 875−889 doi: 10.16383/j.aas.c240258
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240258
关键词
多智能体深度强化学习,两团队零和马尔科夫博弈,最大熵,值分解
摘要
在两团队零和马尔科夫博弈中, 一组玩家通过合作与另一组玩家进行对抗. 由于对手行为的不确定性和复杂的团队内部合作关系, 在高采样成本的任务中快速识别优势的分布式策略仍然具有挑战性. 鉴于此, 提出一种熵引导的极小极大值分解(Entropy-guided minimax factorization, EGMF)强化学习方法, 在线学习队内合作和队间对抗的策略. 首先, 提出基于极小极大值分解的多智能体执行器−评估器框架, 在高采样成本的、不限动作空间的任务中, 提升优化效率和博弈性能; 其次, 引入最大熵使智能体可以更充分地探索状态空间, 避免在线学习过程收敛到局部最优; 此外, 策略在时间域累加的熵值用于评估策略的熵, 并将其与分解的个体独立Q函数结合用于策略改进; 最后, 在多种博弈仿真场景和一个实体机器人任务平台上进行方法验证, 并与其他基线方法进行比较. 结果显示EGMF可以在更少样本下学到更具有对抗性能的两团队博弈策略.
文章导读
两人零和博弈一直是人工智能领域关注的核心问题. 近年来, 随着深度强化学习等新技术的崛起和计算能力的飞速提升, 围棋[1-2]、德州扑克[3]和实时游戏[4]等两人零和博弈中的一些难题的解决方案已经取得巨大进展. 然而许多现实场景通常涉及两个团队之间的对抗, 并同时涉及团队内部智能体的合作, 此类场景通常建模为两团队零和马尔科夫博弈[5]. 近年来, 多智能体强化学习(Multi-agent reinforcement learning, MARL)在多智能体系统领域大放异彩, 特别是在两团队零和马尔科夫博弈应用方面已取得令人瞩目的成功, 例如在复杂游戏 《星际争霸》[6]、《王者荣耀》[7]等中的竞技模式.
许多现有方法将两团队零和马尔科夫博弈简化为两人零和博弈问题进行求解, 如基于类似Bellman算子估计纳什均衡(Nash equilibrium, NE)的方法, 其在每个特定状态下解决阶段性博弈的纳什均衡问题[8-9]. 虽然在理论上可以通过多项式时间的线性规划来解决双人零和博弈的纳什均衡问题, 但随着玩家数量的增加, 其优化过程不可避免地会遇到组合爆炸问题[10]. 基于策略种群的多智能体强化学习方法(Population-based multi-agent reinforcement learning, PB-MARL)将多智能体强化学习与动态种群选择方法相结合[11], 通过自动课程学习进行求解两人零和博弈问题. 此类方法在很多场景中得到广泛应用, 除游戏环境, 还包括《机器人足球》[14]等实际应用. 基于此, 一些工作将PB-MARL与合作的多智能体强化学习算法相结合, 以解决两团队零和马尔科夫博弈问题[15-16]. 然而, 该类方法数据利用率低, 使得在很多样本采集成本高的任务中无法应用. 基于值分解的多智能体极小极大Q学习(Factorized multi-agent minimax Q-learning, FM3Q)[17]方法大大缓解了上述问题, 在解决队间对抗的同时, 还考虑队内信誉分配的问题, 增加数据利用率, 降低计算复杂度. 但FM3Q只能解决离散动作问题, 无法应用到连续动作场景.
为高效地解决不限动作空间的两团队零和马尔科夫博弈任务, 本文将多智能体执行器−评估器框架与极小极大值分解框架相结合, 降低两团队联合极小极大Q函数的训练难度, 并潜在地缓解信誉分配问题. 此外, 为避免在训练过程中陷入局部最优, 引入最大熵评估并将其与分解的个体独立Q函数相结合用于策略改进. 本文的贡献如下:
1)为解决不限动作空间的两团队零和马尔科夫博弈任务, 本文提出一种基于极小极大值分解多智能体执行器−评估器框架, 显式构造基于神经网络的策略评估器和执行器, 同时将联合极小极大Q函数分解为个体独立Q函数用于策略评估, 引导执行器生成不限动作空间的策略, 可以在不限动作空间的任务中提升优化效率和算法性能.
2)在上述框架中引入最大熵以防止在线学习过程收敛到局部最优. 统计策略在时间域累加的熵值用于评估策略的熵, 并将其与分解的个体独立Q函数结合用于策略改进. 本文提出的熵引导的极小极大值分解(Entropy-guided minimax factorization, EGMF)强化学习方法通过值分解降低计算复杂性, 并通过熵最大化增强算法的探索性能.
3)在通用的仿真环境、多机器人博弈仿真场景和实体任务上进行测试, 并与其他基线方法进行比较, EGMF算法以更少的样本实现更加卓越的性能.
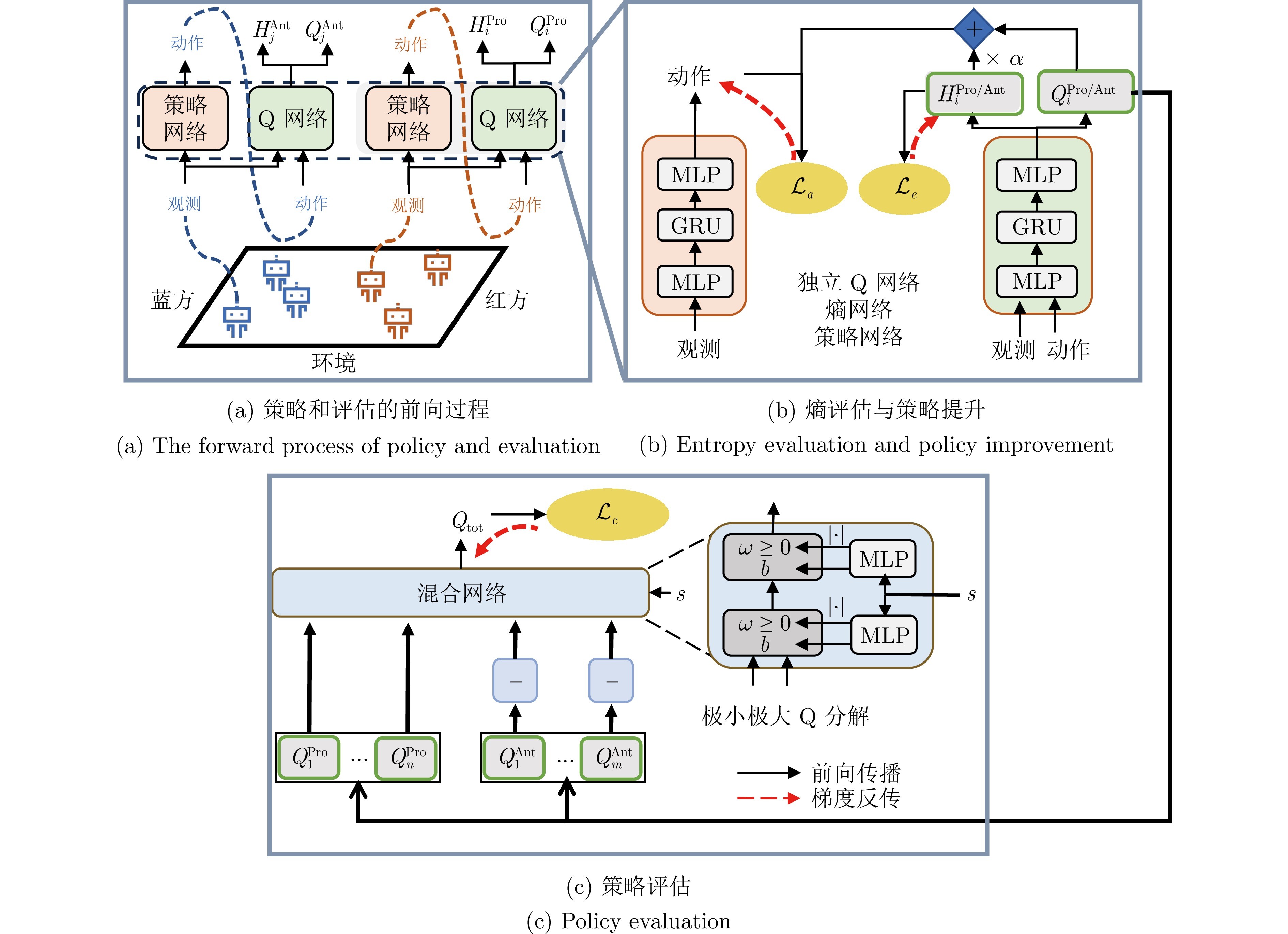
图 1 EGMF的方法架构(EGMF通过联合极小极大Q函数分解框架进行策略评估, 分解的个体独立Q函数与熵评估函数结合用于策略改进)
图 2 实验验证平台(包括Wimblepong 2v2、MPE 3v3、RoboMaster 2v2和现实世界的RoboMaster 2v2)
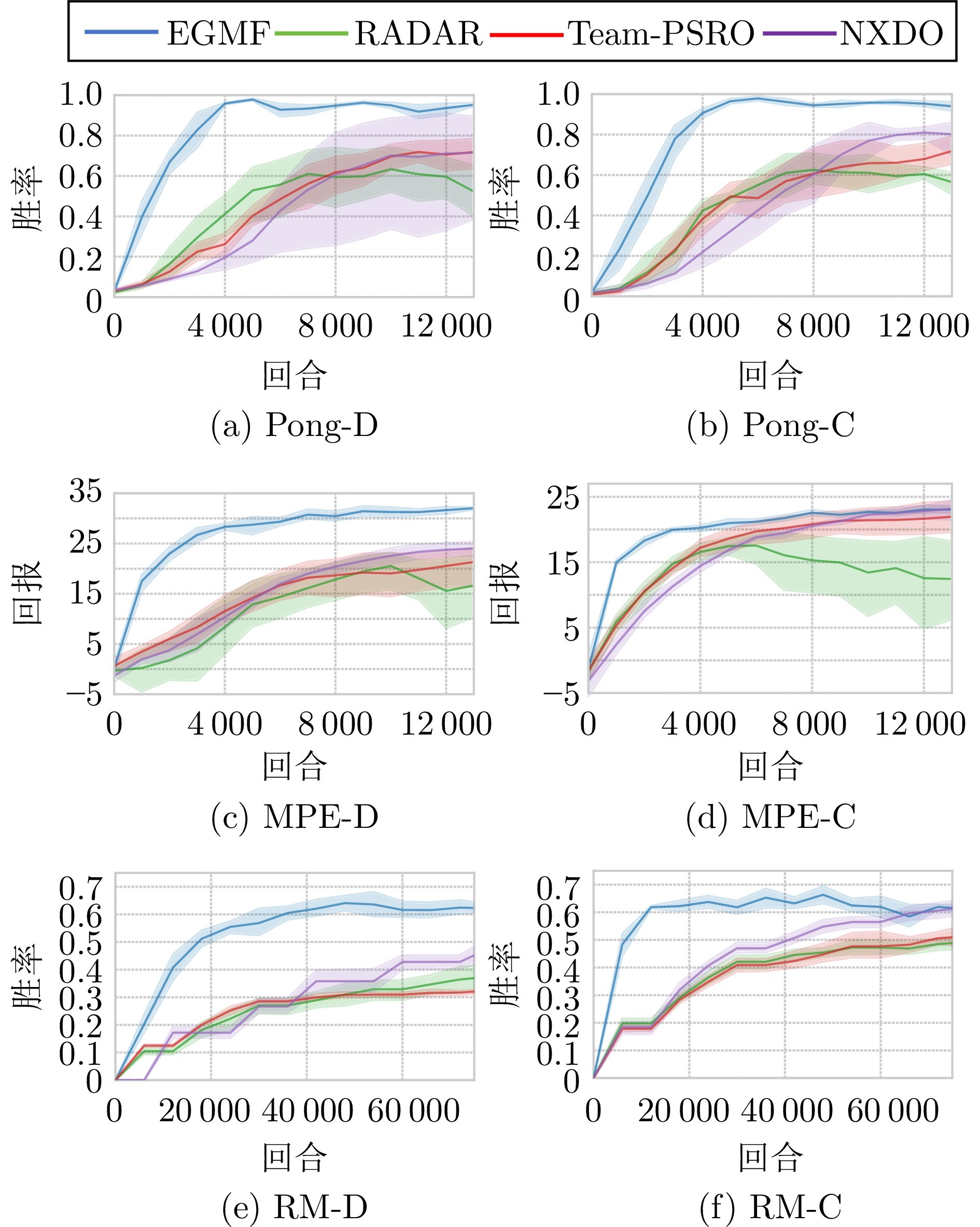
图 3 训练过程中与基于脚本的智能体进行对抗的结果
基于极小极大值分解的两团队零和博弈算法具有数据利用率高、性能优越的特点, 但往往受限于离散动作空间, 且容易收敛到局部最优. 本文为高效处理不限动作空间的两团队零和马尔科夫博弈任务, 提出一种熵引导的极小极大值分解强化学习算法EGMF. 首先, 提出一种基于极小极大值分解的执行器−评估器框架, 在不限动作空间的任务中提升优化效率和算法性能. 同时为避免在线学习过程收敛到局部最优, 引入最大熵使智能体可以更充分地探索状态空间. EGMF利用历史交互数据, 在策略评估、熵评估和策略改进之间进行迭代更新. 相关算法在仿真与实体实验场景验证了其优势, 尤其在与基于规则的智能体进行对抗的评估中, EGMF的优化速度是最优基线算法的2∼5倍. 但是EGMF为保证训练稳定性, 在训练过程中使用的是全部的历史数据, 更加复杂的博弈任务中导致计算量非常大. 因此, 未来我们将在现有算法中使用更加高效的经验回放机制.
作者简介
胡光政
中国科学院大学博士研究生. 2016年、2019年分别获得北京理工大学学士和硕士学位. 主要研究方向为深度强化学习和多机器人博弈. E-mail: hugaungzheng2019@ia.ac.cn
朱圆恒
中国科学院自动化研究所副研究员. 2010年获得南京大学自动化专业学士学位. 2015年获得中国科学院自动化研究所控制理论和控制工程专业博士学位. 主要研究方向为深度强化学习, 博弈理论, 博弈智能和多智能体学习. E-mail: yuanheng.zhu@ia.ac.cn
赵冬斌
中国科学院自动化研究所研究员, 中国科学院大学教授. 分别于1994年、1996年和2000年获得哈尔滨工业大学学士学位、硕士学位和博士学位. 主要研究方向为深度强化学习, 计算智能, 自动驾驶, 游戏人工智能, 机器人. 本文通信作者. E-mail: dongbin.zhao@ia.ac.cn
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1487597.html?mobile=1
收藏