引用本文

张文韬, 张保勇, 袁德明, 徐胜元. 分布式在线鞍点问题的Bandit反馈优化算法. 自动化学报, 2025, 51(4): 857−874 doi: 10.16383/j.aas.c240289

Zhang Wen-Tao, Zhang Bao-Yong, Yuan De-Ming, Xu Sheng-Yuan. Bandit feedback optimization algorithm for distributed online saddle point problem. Acta Automatica Sinica, 2025, 51(4): 857−874 doi: 10.16383/j.aas.c240289

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240289

关键词

Bandit反馈，分布式优化，在线鞍点问题，镜面下降，动态鞍点遗憾 

摘要

本文研究了多智能体时变网络上基于Bandit反馈的分布式在线鞍点问题, 其中每个智能体通过本地计算和局部信息交流去协作最小化全局损失函数. 在Bandit反馈下, 包括梯度在内的损失函数信息是不可用的, 每个智能体仅能获得和使用在某决策或其附近产生的函数值. 为此, 结合单点梯度估计方法和预测映射技术, 提出一种非欧几里得意义上的分布式在线Bandit鞍点优化算法. 以动态鞍点遗憾作为性能指标, 对于一般的凸−凹损失函数, 建立了遗憾上界并在某些预设条件下确保所提算法的次线性收敛. 此外, 考虑到在迭代优化中计算优化子程序的精确解通常较为困难, 进一步扩展一种基于近似计算方法的算法变种, 并严格分析精确度设置对扩展算法遗憾上界的影响. 最后, 通过一个目标跟踪案例对算法的有效性和先进性进行仿真验证.

文章导读

近年来, 在线凸优化已成为一种解决实时决策任务的强有力工具和框架, 并且由于其在传感器网络、机器学习、强化学习、智能电网等领域的重要应用, 而引起了国内外学者的广泛关注[1−4]. 在该优化框架下, 损失函数信息仅在决策者做出决策后才会被对手或环境揭示, 即决策者仅能获取损失函数的后验信息. 通过使用所揭示的函数信息, 决策者更新下一时刻的决策, 继而生成一系列决策以实现最小化累积损失函数的目标. 在线凸优化的开创性工作可追溯到文献[5], 其中该文分析在线梯度下降优化算法并建立了O(√T)的静态遗憾(Regret)界. 到目前为止, 人们针对在线凸优化问题提出了许多有效可行的算法, 如文献[6−11]. 

然而, 在一些重要应用场景中, 如双线性矩阵博弈[12]、约束优化对偶性[9]、高维数据分类[13]、鲁棒优化问题[14]等, 所涉及的损失函数并不适用于在线凸优化框架, 换句话说, 它们的损失函数不总是凸(凹)的, 而是呈现出一种凸凹结构. 因此, 这些实际场景自然地激发了学者们对在线鞍点问题(也称在线最小最大优化)的研究兴趣. 早期, Ho-Nguyen和Kılınç-Karzan[15]使用加权在线鞍点间隙的性能指标, 对集中式在线鞍点问题进行研究并给出了次线性收敛的结果. 在文献[16]中, Rivera等提出一种跟随领导者在线鞍点优化算法, 并对于凸凹和强凸强凹目标函数分别获得了O(√T lnT)和O(lnT)的静态遗憾上界. 随后, Xu等[17]在文献[16]的基础上额外引入了正则化项, 实现了稳定的决策. Wood和Dall＇Anese[18]使用平衡点理论分析了一类具有决策相关数据的在线鞍点问题. 

在很多实际场景中, 例如网络中的在线路由、发电、网络搜索中的在线广告投放[2, 9], 损失函数的具体信息是不可用的, 且智能体仅能获得和使用某决策处或其邻域内的函数值. 这种信息反馈模型称为Bandit反馈. 为此, 利用函数值信息构造单点和多点梯度估计器的解决方案随之引起关注[9, 11, 19−23]. 对于一类在线矩阵博弈问题, Cardoso等[23]分析了全信息和Bandit反馈下的纳什均衡遗憾. 在文献[22]中, Roy等在两种信息反馈下研究了非平稳鞍点问题的两种集中式优化算法, 并详细展示了所设计的算法在动态和静态鞍点遗憾标准下是次线性收敛的. 然而, 这一结果依赖于目标函数为强凸−强凹和光滑的强假设条件. 受限于单个机器的计算瓶颈, 集中式算法往往难以胜任大规模复杂的优化问题[3, 24]. 相比之下, 分布式框架下的算法避免了这个限制, 且因其低计算负担、结构鲁棒性和隐私性等显著优势, 近年来已引起国内外学者的广泛关注[3, 9−10, 24−36]. 在此框架下, Zhang等[37]提出一种Bandit反馈下的基于两点梯度估计方法的分布式在线鞍点优化算法, 并建立相应的次线性动态鞍点遗憾. 

就在线Bandit鞍点问题的分布式解决方案而言, 现有的研究尚不完善, 新的分布式算法亟待开发和分析. 此外, 包括文献[37]在内的传统欧氏距离下的算法缺乏灵活性, 难以进一步利用优化问题的某些性质. 例如, 对于带有单纯形约束的优化问题, Kullback-Leibler (KL)散度作为一种非欧距离可获得算法显式表达, 而对于传统的欧氏距离则无法获得[8]. 因此, 开发一种非欧几里得意义上的分布式在线Bandit鞍点算法是必要且有意义的. 另一方面, 由于无偏估计性质和仅需一个采样点的要求, 单点估计框架能够有效处理Bandit反馈下梯度信息受限情形, 且可以与许多应用相兼容, 例如网络搜索中的在线广告投放[2, 9]. 受上述两方面分析的启发, 本文应用单点梯度估计框架和分布式镜面下降方法, 研究了在线Bandit鞍点问题, 主要贡献总结为如下三个方面: 

1) 为解决时变多智能体网络上的分布式在线Bandit鞍点问题, 本文通过结合梯度估计和时变预测映射技术, 提出一种非欧几里得意义上的分布式在线算法. 在距离度量上采用更为一般的Bregman散度而不是传统的欧氏距离, 使得算法由于对不同优化问题的自由选择性而变得更加灵活. 此外, 受益于预测映射的灵活设置, 所提算法可实现比单位映射更好的收敛性能. 

2) 开发并分析基于单点梯度估计器的分布式在线Bandit镜面下降鞍点优化算法. 区别于文献[37]的两点估计方法, 每个单点估计器仅要求一个函数值, 且其估计参数不依赖于总迭代时间T的先验知识, 进而有效增强了算法的可操作性和实用性. 对于一般化的凸凹损失函数, 建立了其动态遗憾上界并保证了次线性收敛. 

3) 考虑到在迭代优化中计算优化子程序的精确解通常较为困难且计算成本昂贵, 本文设计一种基于近似计算方法的算法变种, 并严格分析精确度设置对算法遗憾上界的影响. 最后, 通过一个目标跟踪案例对算法的有效性和先进性进行了仿真验证. 

本文内容安排如下: 第1节描述所研究问题和一些预备知识; 第2节给出一种分布式在线Bandit鞍点优化算法和对应收敛结果; 第3节给出一种基于近似计算方法的算法变种; 第4节给出仿真实验结果; 第5节对本文进行总结与展望. 

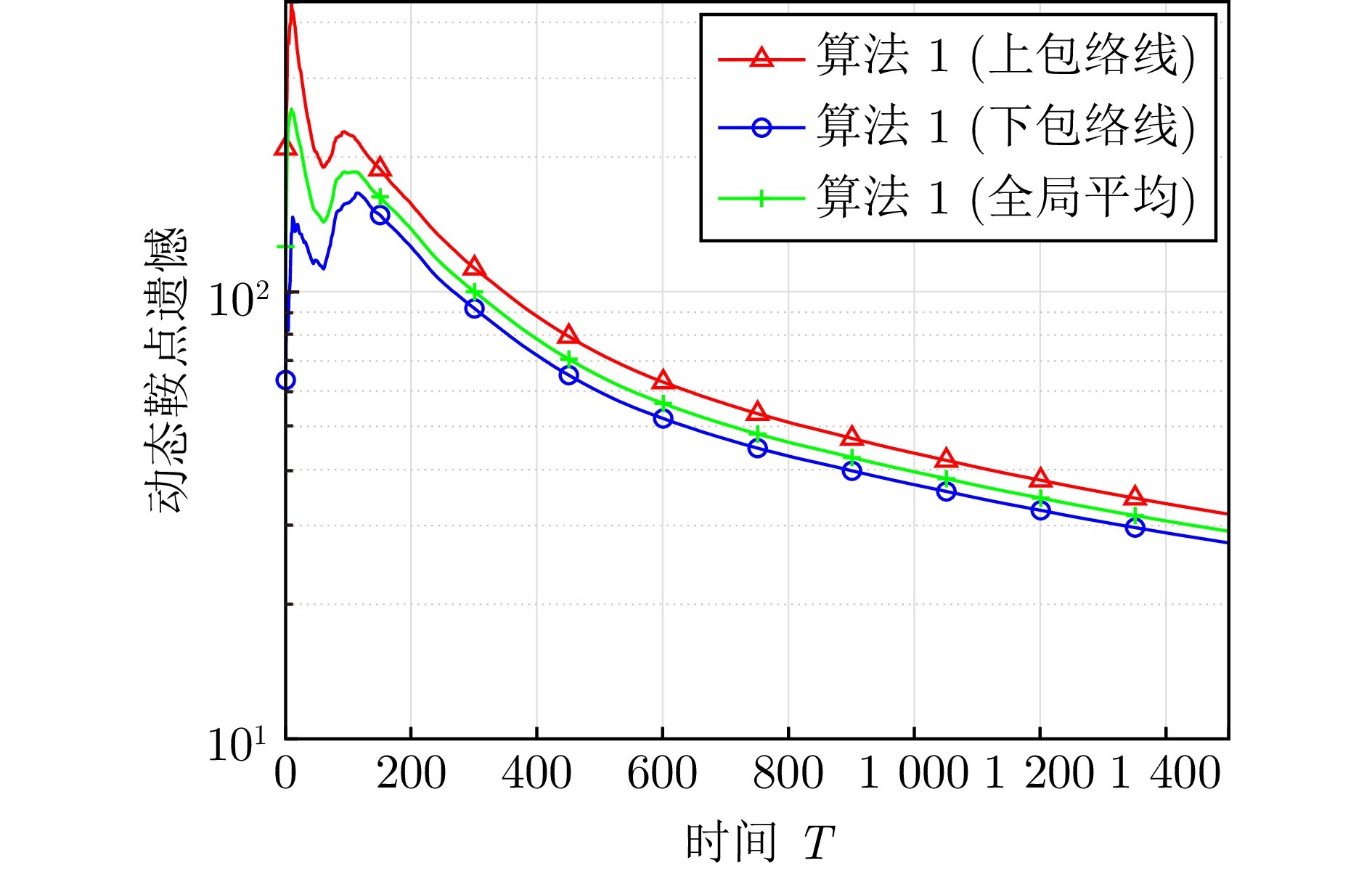
图 1  算法1的收敛性

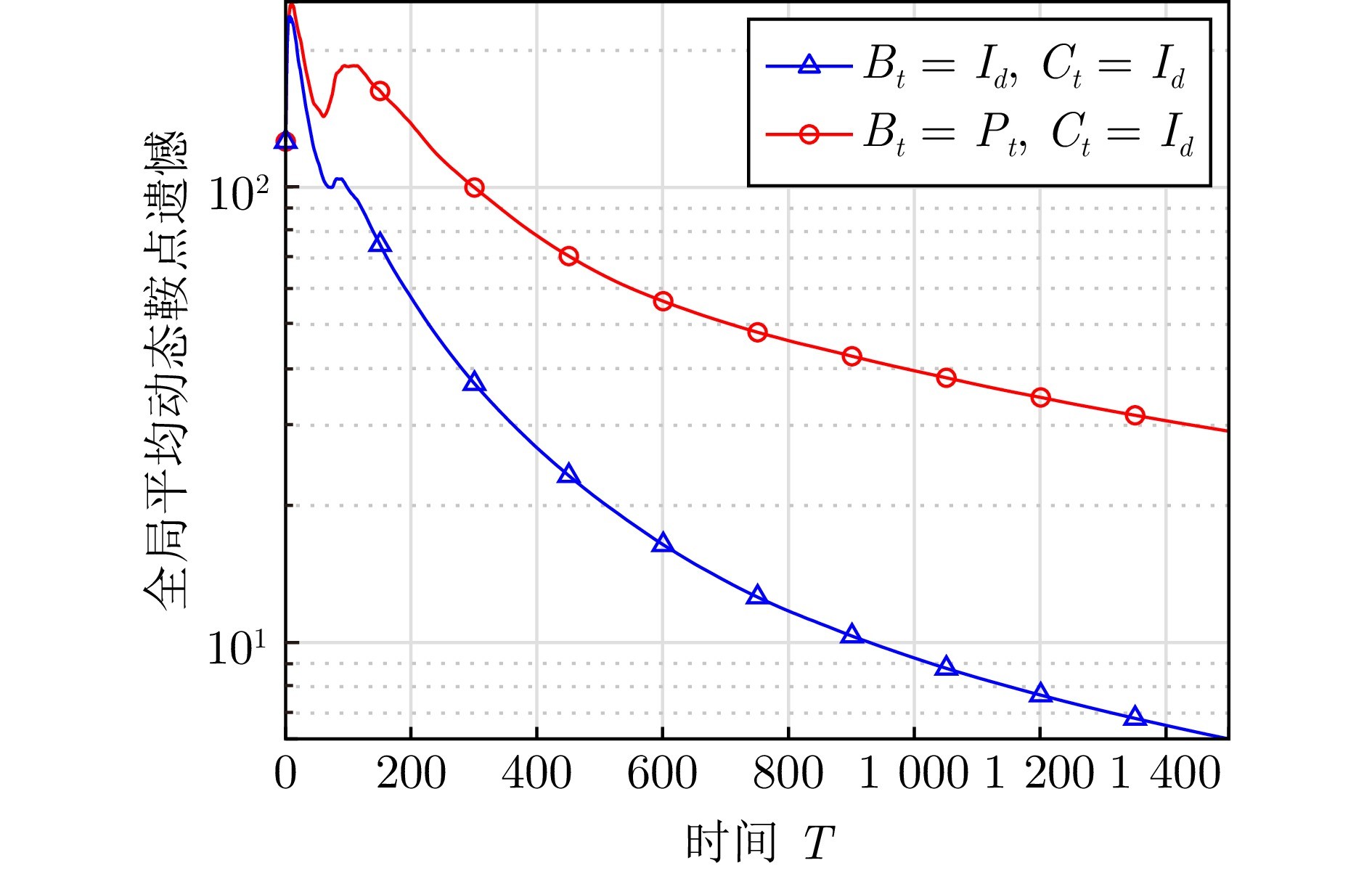
图 2  不同B_t和C_t下算法1的对比结果

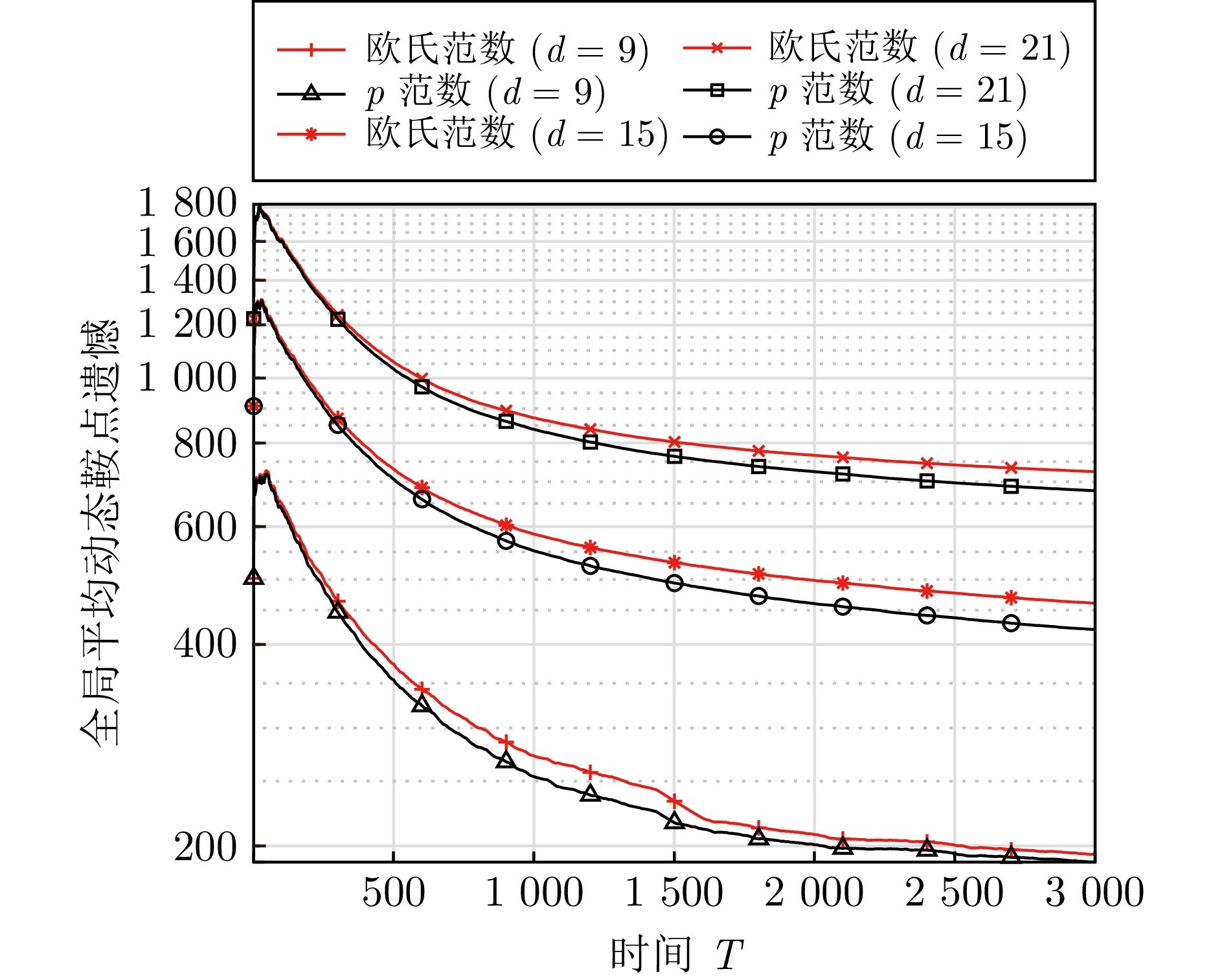
图 3  不同d选择下带有欧氏范数与p范数的算法1对比

对于一类多智能体时变网络上的分布式在线鞍点问题, 本文研究损失函数具体信息不可用的情形, 即Bandit反馈. 通过引入单点梯度估计器并结合预测映射技术, 开发一种高效的非欧几里得意义上的分布式在线Bandit镜面下降鞍点优化算法. 对于一般的凸凹目标函数, 证明了所提算法在某些预设条件下可实现次线性动态遗憾. 值得注意的是, 所提算法的每个梯度估计仅需一个函数值且算法参数消除了对总迭代时间T先验知识的依赖, 这极大地增强算法的实用性. 此外, 考虑到在迭代优化中计算优化子程序的精确解通常较为困难且计算成本昂贵, 本文进一步设计一种基于近似计算的算法变种, 并严格分析精确度设置对算法遗憾上界的影响. 最后, 以目标跟踪问题作为仿真案例, 对所开发算法的有效性和先进性进行有效的验证. 未来, 放宽凸凹条件将是一个充满兴趣但富有挑战的研究. 

作者简介

张文韬

南京理工大学自动化学院博士研究生. 主要研究方向为多智能体分布式优化, 鞍点问题. E-mail: iswt.zhang@gmail.com

张保勇

南京理工大学自动化学院教授.主要研究方向为多智能体分布式优化与控制, 时滞系统和非线性系统的分析与控制. 本文通信作者. E-mail: baoyongzhang@njust.edu.cn

袁德明

南京理工大学自动化学院教授. 主要研究方向为多智能体分布式优化与控制, 分布式机器学习. E-mail: dmyuan1012@gmail.com

徐胜元

南京理工大学自动化学院教授. 主要研究方向为广义系统、时滞系统和非线性系统的分析与控制. E-mail: syxu@njust.edu.cn