以下的六个科学问题都是数学领域的问题，它们也是克雷数学研究所选出的七个突出数学问题，其中第1个问题在科学问题(19)计算机的运算极限中已经进行了介绍(也就是P vs NP问题)。下面开始逐个解读剩余的六个数学问题，要想更详细地了解克雷数学研究所选出这七个千禧年数学问题，请访问克雷研究所的网站。

120. 是否存在一个简单的方法来证明椭圆曲线是否有无限个有理解？

Is there a simple test for determining whether an elliptic curve has an infinite number of rational solutions?

题记：具有y² = x³ + ax + b这种形式的椭圆曲线方程是一个强大的数学工具。贝赫(Birch)和斯维纳通-戴尔(Swinnerton-Dyer)猜想(BSD猜想)告诉我们如何在有理数范围内确定椭圆曲线有多少个解，如果BSD猜想正确，那么它可以用来解决许多问题。读懂本文必须具备群论的基础知识。

1. 数字、数域和方程

数学源自于人类计数的需要(当然为什么需要或能够计数，你可以认为这源于物质世界是可以被分割的结构这样一个客观现实)，所以人类发明了数字(1, 2, 3,......)和计数方法。简单点讲数学就是研究数字之间相互关系的科学。显然，最自然的数就是自然数1, 2, 3, .....，全体自然数的集合一般用N表示。由此可见自然数是数学的基础。

图1 计数用的加法和乘法以及乘法中的平方数

在自然数N上为了表达没有或空就引入了0，接着为了表达亏欠就引入负数，而这些数一起就构成了整数集合Z。可见，数字之间最直接的关系就是计数用的加法关系，引入加法的逆运算减法就能从自然数中产生0和负数，可见运算规则可以扩充数的集合。然而在实际计数的时候人们还发现了一种更为快捷的计数方法：乘法。如图1所示，一堆石头需要计数是多少个，可以用加法一个地一个数，也可以放成几行几列，然后用乘法来更快地计数。乘法的引入带来了逆运算除法(除法就表示分组或分割)，而除法的运算又带来了和我们这个问题有最重要联系的数学概念有理数集合Q：如果一个数能表示成两个自然数相除的形式，就称为自然有理数。当然如果考虑0和负数，也就是能表示为两个整数相除的形式就称为有理数。用数学语言表示就是：能表示为p/q的数, 其中p为整数，q为整数。而数学上p/q如果不等于整数时叫做分数，如果p/q等于整数时p称为q的倍数，q称为p的因数，可记为p|q。显然以上的有理数概念里有一个非常特殊的数，就是分母q=0的有理数，我们一般将其称为无穷大∞。当然无穷大由于过于特殊一般都要单独拿出来进行说明是否包括在有理数的集合里。这里引入数集合里的数域概念，数域(number field)就是在加减乘除运算(四则运算)运算下保持封闭的数的集合，比如最常用到的有理数集合Q就是一个数域，其中就需要包括无穷大∞。

有了有理数域的概念之后，人们又发现了自然数通过乘法还能得到不是有理数的数，即无理数。发现无理数的一个最重要的乘法运算就是如图1所示的自己和自己相乘得到的自然数，也就是能够摆成方块的平方数，然后对自然数引入平方的逆运算就是开方(如此推广如立方、n次方等及逆运算)。继而有理数和无理数一起构成实数域R。开方运算在自然数上不仅导致了无理数的发现，而且在整数中负数上的开方还引入了复数的概念：-1的开方等于i，复数的集合用C表示，也构成复数域C。本问题就是要在一定数域上讨论数的关系，比如平方数和立方数之间的关系。

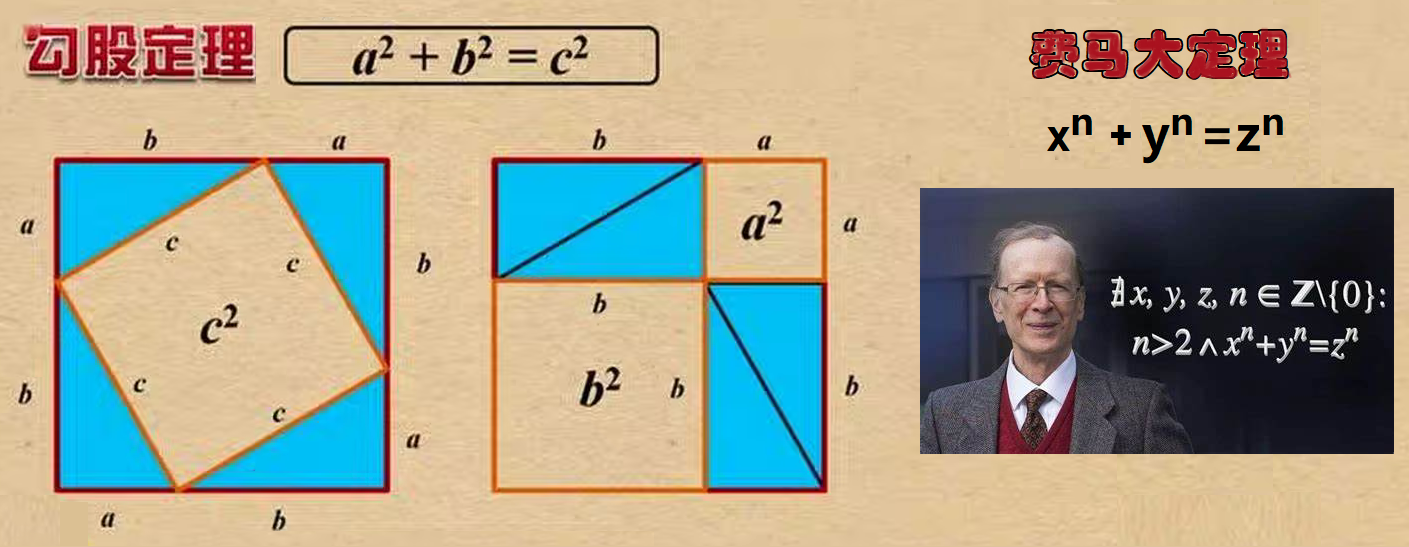
数学家研究数字之间关系的时候，发现了许多让人惊叹的联系，比如上面提到的自然有理数p/q，如果p和q没有公因数或最大公因数是1就是互质关系(数学上表示为gcd(p,q)=1)；自然数中没有因数的数(除了自己和1，即图1中不能分成方块的数)就称为素数(数论的很多定理都与它有关)等等。而表达数字之间经常用到的关系式就是方程，例如表达平方数之间关系的式子：x² +y² = z²，这个式子中最为重要的关系符号就是“=”，它几乎是数学研究的核心符号(后来在不同对象上推广为等价、同构、同胚等概念)。上面的关系称为代数方程，它有三个代表数字的代号x , y, z(代数)，称为三元方程，最高乘方次数为2，称为三元二次代数方程。以上的三元二次方程给出的数字间的关系和著名的三角形勾股定理有密切联系：如果直角三角形三条边长为a, b, c的话，那它们就满足上面的关系：a² +b² = c²。数学家对这种代数方程关系所给出的解有着非常狂热的好奇和追求，比如x³ +y³ = z³的解(x, y, z)在整数范围内是什么？这个问题包括方程是否有解(解的存在性)？如果有解是什么解(解的唯一性、有限性、分类等问题)？比如有一个和本问题有紧密联系的数学问题：费马大定理(Fermat’s Last Theorem)

三元 n 次方程 xⁿ  + yⁿ  =  zⁿ, n > 2 在自然数范围内有没有解？

费马大定理的结论是：解不存在。这个定理在1995年前还叫费马猜想，因为1995年被美国数学家安德鲁·怀尔斯(Andrew Wiles)最终证明。而且这个证明中用到了一个二元(x, y)三次方程所定义的平面曲线：椭圆曲线，它在证明费马大定理中起到了关键的作用(怀尔斯证明费马大定理论文的题目就是：Modular Elliptic Curves and Fermat's Last Theorem)，而其中的椭圆曲线(Elliptic Curves)就是本科学问题所要重点讨论的对象。下面我们将120个科学问题所要讨论的问题再做一个重新的描述：对于椭圆曲线，它的解集(x, y)在有理数范围内是有限还是无限的？

为了搞清楚这个问题，我们首先要科普一个重要的概念：椭圆曲线。

2. 椭圆曲线 (Elliptic Curves)

简单地来讲，椭圆曲线是由下列二元三次方程所定义的平面曲线：

其中a和b是参数。a和b可以取整数Z、有理数 Q 或实数R，无论如何要求系数的判别式Δ ═ -16(4a³+27b²)不等于0。当然最为有意思是a和b都取整数时情形，而且一般常在实数域上考察椭圆曲线(1)的解(x, y)。所以这里需要明确椭圆函数的定义数域，如果解(x, y)在某个数域K上取值，我们就称椭圆曲线是在K域上的椭圆曲线，因为不同数域上的椭圆曲线不仅形式和图像不同，而且求解的难易程度也不同。上面的形式(1)被称为魏尔斯特拉斯形式(Weierstrass form)，这是在有理数域Q、实数域R上椭圆曲线最一般的标准形式(当然在其他数域K上式(1)并不一定是一般形式，这个结果来自于莫德尔-韦尔定理Mordell-Weil Theorem及其推广情况，这里会涉及数域K的其他性质，为避免复杂不在此讨论)。

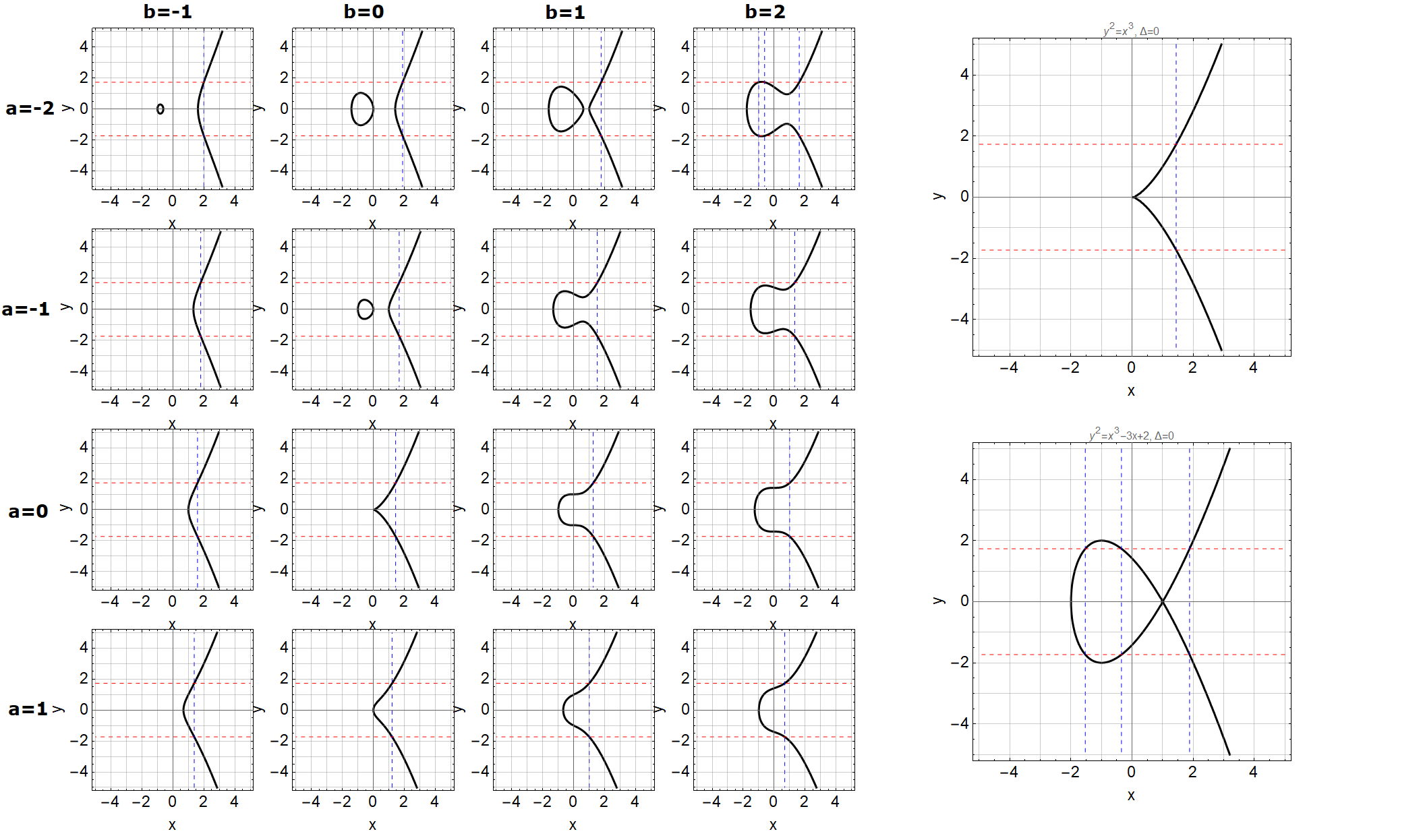
图2 椭圆曲线图像和奇异的椭圆曲线

椭圆曲线之所以叫椭圆曲线是因为该曲线和计算椭圆周长的积分有关(本网站也有很多博主有介绍，如张天蓉网友的博文，也可参考文献：科学通报61(34)3638, 2016)。为了对椭圆曲线有一个直观的认识，图2中展示了不同a和b参数(图中取整数)下的椭圆曲线图像(椭圆函数的实数解就是曲线上连续的点，在其他数域K上椭圆函数可能是一些离散的点，在复数域C上还是一个环面)。在这些图像中判别式Δ为零的曲线，如图2右边所示的两个曲线都是奇异的曲线，上图曲线在(0,0)处存在一个尖角，而下图的曲线自己和自己相交，这两种情况都表示椭圆曲线不光滑(存在导数不连续的点)，所以(1)式所定义的椭圆曲线应该是光滑的椭圆曲线，不包括那些不光滑的特殊情况。

根据图2中椭圆曲线的图像，我们可以对椭圆曲线所表达的解给一个集合上的表述：所谓实数域上光滑椭圆曲线是指以下的集合：

显然 E(R) 的集合是一个由实数对(x,y)为元素组成的集合，也就是图2所示的椭圆曲线上的所有点连成的线，集合的元素自然是无穷多个。当然如果在有理数域上椭圆曲线的集合则表示为：E(Q)。利用集合概念，第120个科学问题可以重新表述为：对于椭圆曲线E(R)集合中有理数元素(或者对于E(Q)集合的元素)的个数是有限的还是无限的？也就是说图2中光滑椭圆曲线上的点中有理数点的个数是有限的还是无限的？

这个问题直观上看好像有理数的解应该是无限的(因为实数解就有无限多个)，然而了解下面一些关于这个问题的结果和定理，你对这个问题就会产生不同的认识。

3. 一些相关的结果或定理

首先1983年, 法尔廷斯(Faltings)证明了次数大于3的光滑平面曲线只有有限个有理数解。那么对于次数等于3的椭圆曲线，由于它处于有限和无限的临界点，这个问题却变得非常复杂了。数字3一直都是个非常特殊的数，比如除了费马大定理以外拓扑学中还有一个著名的庞加莱猜想(任何一个单连通的闭的n维流形一定同胚于一个n维的球面)。对于n >3的情况很容易就被证明了，但对于n=3的情况到2003年才被格里戈里·佩雷尔曼证明(2006年数学界才最终认定)，所以一般把最难的n=3的情况才称为庞加莱猜想。

对于椭圆曲线这类二元三次方程，其有理数解的个数目前并没有最后结论，但其中有以下的重要结果：对于有理数域Q上的光滑椭圆曲线E(Q)，其元素构成一个群，而且该群是有限生成的阿贝尔群(finitely generated Abelian group)，这个结论被称为莫德尔-韦尔定理(Mordell-Weil Theorem)。这个定理最终在广义的数域K(如整数F_p域、有理数域Q、实数域R、复数域C)上都被证明成立：

Mordell-Weil Theorem:  Let E be an elliptic curve defined over a number field K. The group E(K) is a finitely generated Abelian group.

当然对具体的数域K如实数域上的E(R)也都构成一个有限生成的阿贝尔群(有限个群元通过群运算产生的交换群)，为了更加直观，我们还是在实数域R上先利用曲线来方便考察椭圆曲线集合E(R)构成的群结构，之后再回到E(Q)群上，然后在讨论密码学时再讨论整数F_p域上的椭圆曲线的离散群E(F_p)，之后适当讨论复数域C。

图3 实数域椭圆曲线的加法运算

如图3(a)所示，取椭圆曲线上的任意两点P和Q，通过P和Q做一条直线，其一定和椭圆曲线相交于R点，对于这三点有如下的关系：P + Q + R = 0。这里首先需要注意，这里的群运算+不是数域上的加法运算(P + Q不是直接将P和Q 点的坐标相加，具体的加法操作在下面给出)，用直线能形象地给出点的对应关系，而0是指群运算+的单位元；其次图3中(b)和(c)的情况指P = Q的切线情况(两点靠近为切线)，而和y轴平行时的线(d)(e)和椭圆曲线的交点从图像上看应该是无穷远的点，而这个无穷远的点就是群的单位元0点(这一点似乎有些抽象，可以认为无穷远点就是群的单位元0)，所以椭圆曲线E(R)如果引入无穷远点作为单位元0后，就构成了一个封闭的具有加法性质的交换群：

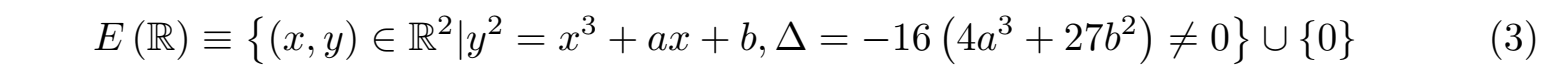
显然从群的角度看图3(d)中P和Q就是互逆的元素(Q = -P)，也就是椭圆曲线上关于x轴对称的点(x,y)和(x,-y)的两个元素是互逆的，这也来源于椭圆曲线y²项的对称性；根据图3的图像，我们可以发现椭圆曲线上三个点总满足 P + Q + R = 0 (无论有没有重复)，根据这个等式可以给出E(R)中两个群元P和Q的群加法运算规则 P + Q 。如图3的(a)或图4(a)所示，设三个点的坐标分别为：

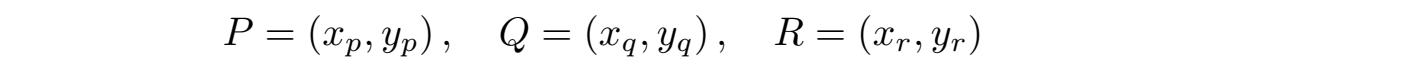
首先当P和Q不同时，根据 P 和 Q 的坐标计算直线 y = kx + c:

此时直线的斜率 k 和 c 分别为：

利用直线方程计算直线和椭圆曲线的交点即可得到如下结果：

其次当P = Q时，如图3(b)(c)所示，此时的直线为切线，带入(6)式的斜率k和截距c分别为：

以上的这些算法有现成的程序可以使用，利用程序可以非常准确地验证群+运算给出的结果：P + Q  = -R 就是元素R点的逆元-R=(x_r,-y_r)，显然它依然在E(R)中。利用这个运算规则我们可以进一步检验群加的交换律、结合律等等，最后可以证明(3)式所定义的集合E(R)确实是一个交换群。椭圆曲线的群结构预示着群中的元素可以通过群元的加法来不断产生，见下图4(a)所示，用P点和Q点的加可以产生-R，用-R的逆产生R，然后用P和-R的交点产生S和-S等等，这些不断产生的元素都属于包含P和Q的同一个子群。

图4 实数域上椭圆曲线的群结构

椭圆曲线群结构的另一方面，如图3(e)表达的结果: P + P = 2P = 0，这种情况表示(e)中的这个点实行了自己到自己的群操作后就等于单位元0，如此可以定义群的数乘nP,n是自然数。注意在一般的群论里群元素自己对自己的操作经常写为P² ，但此处的群运算+具有“加法”的性质，所以才有这样的乘法：3P = P + P + P,如此等等。在群理论里有一个循环群(Cyclic group)的概念，就是整个群都由群元g自己和自己的群操作生成，如果至少操作n次后等于群的单位元，则这个n叫生成元g的阶(循环周期)，也是该群的阶(群元的个数),群可标记为C_n。如果这个群的生成元是整数Z，那么阶为n的整数循环群就记为Z_n。所以图3(e)中的那个点P = (x, y)的阶就是2，它的运算规则根据椭圆曲线可以这样计算(2P的x坐标)：

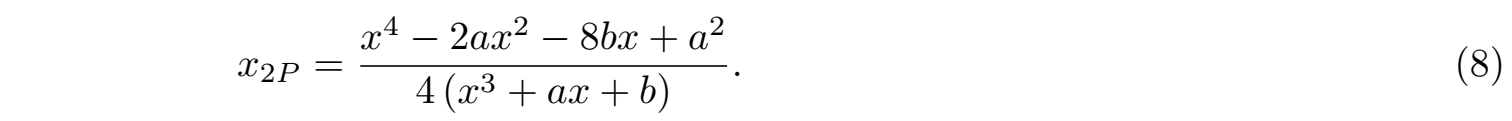
然而椭圆曲线上还有3阶、4阶、5阶等等很多不同阶的点(mP = 0, m < ∞为有限自然数)，而这些点和群加法一样也可以用来产生E(R)群中的元素，而它们构成不同阶的有限循环子群。椭圆曲线群的这些性质都在说明这个实数域上的阿贝尔群一定具有某种群结构。根据以上对实数域上椭圆曲线群的生成计算，我们可以发现，在实数域R上椭圆曲线E上的点组成的这个有限生成的阿贝尔群，应该是一个可解的连续对称群，而这个群同构于单位圆循环群S¹(见图4(a)所示)或同构于直乘群S¹×C₂(见图4(b)所示)。

特别地对于数域K是有理数域:K = Q，根据莫德尔-韦尔定理，群E(Q)是E(R)的子群，而且是分立群，根据有限生成阿贝尔群理论，群结构由梅热定理(Mazur Theorem)给出：

显然椭圆曲线群E(Q)可分解为两个子群的直和，其中T是所谓的扭子群(torsion subgroup)，这个扭群T是一个由有限个元素组成的阿贝尔群，包括E(Q)中所有的有限阶元素，对其的研究已经比较清楚。数学上有限扭群T是和整数循环群Z_n(n为1到10的自然数加上12)以及Z_2m⊕Z₂(m为1到4)共15个群中的某一个同构，所以扭群T做为有限群来说其最高阶不超过16(注意T子群可能存在不是循环群的情况，如Z₂⊕Z₂，这种非循环情况可以理解为两个循环群Z₂扭了一下直和构成的，所以叫扭群)；而群Z^r就是整数域上r个整数群的直积，表示有限r个无限群的直积群，其中r就称为椭圆曲线群E(Q)的秩(rank)。注意秩可以理解为阿贝尔群生成元的个数，所以以上公式(9)所代表的有限生成群E(Q)可以重新表述为：E(Q)中任何元素P都可以被群中一组有限的元素{P₁, P₂, ..., P_t}表示为

显然对于(10)式来说群E(Q)又构成了一个线性空间，代表任何元素都可以被一组独立的元素生成，也就是任何群元素P都可以在一组基P₁, P₂, …, P_t下对应一个整数坐标，这个坐标的维度t(维度t是确定的，它不随基的不同选择而改变)和群秩r有关(要去除有限阶元素以后的空间维度，所以r代表有多少能生成无限群的元素，r=1表示有1个能生成无限群的元素，r=0则代表没有生成无限群的元素，表示此时E(Q)群只是有限T群)，所以这个r一般很难计算，因为它代表群中有几类和无限整数群同构的元素，注意r是无限群的维度，所以在整个有理数域上非常难以计算，但可以通过在有限的整数余数循环域F_p上来进行计算，这种叫E(Q)群代数秩的模算法，后面我们再具体讨论。

对于式(9)中的无限群Z^r中的秩r的问题，也就是椭圆曲线群代数秩的情况目前并不清楚，比如有没有计算代数秩r的有效算法，秩r的可能值会有哪些(比如已经发现了秩r = 27的高秩椭圆曲线等)，r有没有上界等等问题，所以对有理数椭圆曲线秩r有很多猜想，比如有猜想认为：存在秩r任意大的椭圆曲线。现在对秩r的最好结果是Bhargava和Shankar证明的一个结论(获2016年菲尔兹奖)：有理数域上所有椭圆曲线秩r的平均值小于1。椭圆曲线秩的问题是本科学问题所关心的核心，正因为r的不确定性和难以计算的特点，才导致了椭圆曲线在密码学中的应用。下面我们就在有限的整数余数循环域F_p上来考察和计算一下有限域的椭圆曲线群及其秩的问题。

4. BSD猜想

椭圆曲线领域有一个最重要的猜想：BSD猜想，为计算椭圆曲线的秩提供了一个思路。在介绍BSD猜想之前有两个重要的概念需要介绍。首先介绍一下有限数域F_p，其中p为一个素数，它是所有整数对p取模余数的集合：F_p={0, 1, 2, ..., p-1}(p不是素数时不是数域)。在数域F_p上的椭圆曲线就是(3)式中所有变量x,y在数域F_p中取值，而参数a,b可以取使判别式Δ不为零的任意整数(Δ也要取模)，这样的椭圆曲线群记为E(F_p)，它是一个在模mod p运算下封闭的有限群。对于数域F_p上的椭圆曲线，对任意不整除判别式Δ的素数p都可以认为是对有理数域上椭圆曲线群的一个好的模约化(good reduction at p)。举一个例子，例如对于取素数p = 17的数域F₁₇上的椭圆曲线为：

此时在模曲线(11)上计算群加法时依然利用(5)-(8)式进行计算，只是计算时所有加减法和乘除法都是在模运算mod 17下进行的。比如用E(F₁₇)中的点P=(11,3)和点Q=(14,8)计算P + Q点，将坐标带入(5)式和(6)式，可以计算出E(F₁₇)中的另外一个点-R，注意在计算的时候加减乘除四则运算都要用模加法、模乘法进行，比如计算斜率时的除法要用乘法的逆来计算，斜率因此要写为k = 5/3 = 5×3^-1，其中的3^-1表示3在数域E(F₁₇)中的逆元：6，所以k的计算结果应为：Mod[5×6, 17] = 13(其中Mod[]是mathematica取模函数)，所以计算中的每一步都是在取mod 17下的运算。同样计算2P也要用(8)式在模操作下进行计算，最后我们可以反复通过群操作计算得到群E(F₁₇)中的所有有限点(如图5所示)。

图5 椭圆曲线E(F₁₇)的图和群运算表

显然从图5中可以看到在有限数域上的椭圆曲线群E(F₁₇)是由有限的点组成的，其群的元素个数(群阶)为15。当然如果p取更大的素数，则椭圆曲线群的元素个数一般会更多(因为数域F_p的范围也会越来越大，当然其元素个数最多不会超过2p+1,平均大概就是N_p ∽ p+1,见图6左图)，比如p = 37的群E(F₃₇)，其元素就变成了45个，计算结果发现此时群可以分解为两个循环群的直积：C₃×C₁₅。这里有一个定理用来估算群E(F_p)中元素的个数(Hasse’s Theorem)：群E(F_p)中元素的个数N_p的范围满足：|N_p - (p + 1)| ≤ 2(参见下图6右图所示)。所以当椭圆函数群E(F_p)在p很大的时候，群E(F_p)也非常大，这样可以用来进行加密计算。具体用于加密的算法依赖于称为椭圆曲线分立对数的问题(ECDLP: Elliptic Curve Discrete Logarithm Problem)，也就是在群E(F_p)中找两个元素T和S，寻找它们之间满足T = mS的整数m,其中最小的m被称为分立指数(指标)。当然你可以随机地选择一系列整数利用(8)式进行计算直到找到m，然而这个算法的复杂度和群的大小有关，这个问题的算法复杂度比P问题要难，但比指数NP问题简单，所以称为亚指数难度问题。

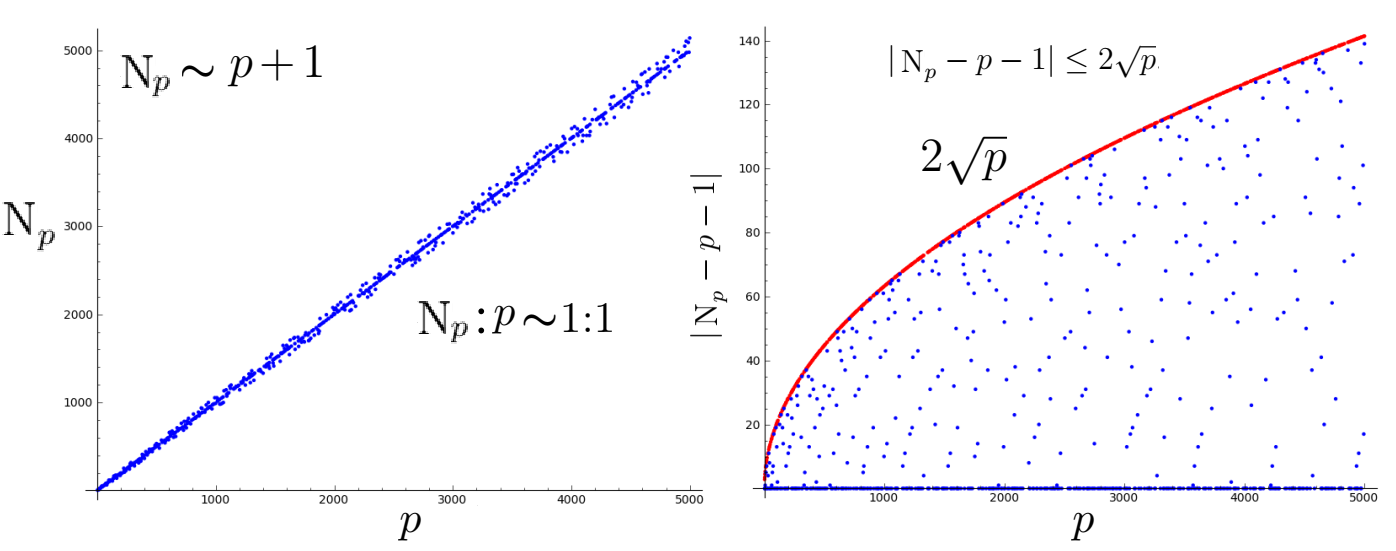
图6 群E(F_p)的群元数N_p和p的关系 图中计算了5000以内所有素数

总之，椭圆曲线从有理数域的E(Q)群到有限域F_p的模约化给出了E(Q)到E(F_p)的一个群同态(group homomorphism)对应，即E(Q)中的有理数点P可以同态对应到E(F_p)的点P* = P (mod p)上，此处不做详细说明。为了介绍关于椭圆曲线群秩有关的BSD猜想，我们再来引入一个重要的椭圆曲线的哈斯-韦伊(Hasse-Weil) L函数。L函数是一个变量为s∈C的复变量函数，定义如下：

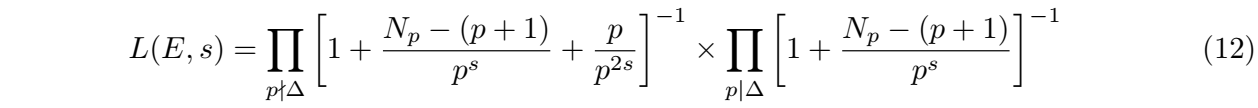
对于L(E,s)函数可以这样计算，对于椭圆曲线可以不断取不整除判别式Δ的素数p，然后在模约化群E(F_p)上计算群元素的个数N_p，然后不断带入如下的L(E,s)函数中(不存在Δ被p整除的项):

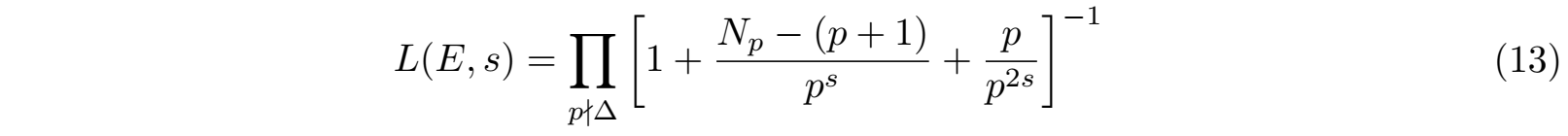
以上的L(E,s)函数可以证明在s的实部Re(s) > 3/2时是收敛的。对于(13)式所定义的L(E,s)函数在临界点s=1处的行为可以证明具有下列性质：

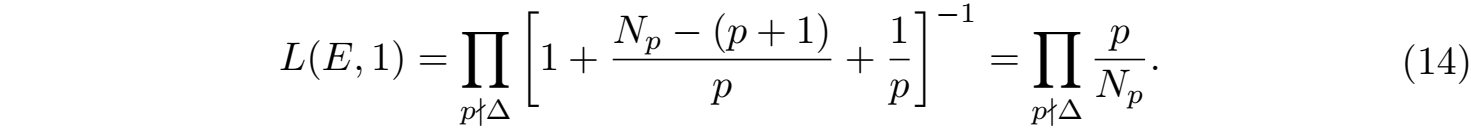
显然由(14)式可见，当群E的规模N_p很大的时候必然有L(E,1) = 0。所以根据这个性质BSD三个人就猜想，如果有理数域上的椭圆曲线群E(Q)是无限的即N_p = ∞，那么就一定会有L(E,1) = 0，这就是BSD猜想的主要思路。为了得到L(E,s)函数在临界点s=1处的性质，经常做的方法就是将L(E,s)函数解析延拓到整个复平面，并将其在 s =1处做泰勒级数展开进行解析分析，就可以得到该函数在s =1点的解析渐进性质：

上式(15)中的这个r_an就被称为是L(E,s)函数在s=1处的解析秩(analytic rank)(前面(9)式中的r称为椭圆曲线群的代数秩)，这样BSD猜想就可具体表述为：对每个椭圆曲线E，其L函数在s=1处的解析秩就等于椭圆曲线的秩：r_an = r。BSD猜想表明通过对椭圆曲线所有素数模约化群的计算可以确定有理数椭圆曲线E(Q)群的秩，也就是能确定到底需要多少个有理数点能用来产生整个E(Q)群，或者能够确定E(Q)是有限还是无限的。根据式(15)可以证明如果此处的解析秩r_an=0,则群的秩就等于0，如果解析秩r_an=1,则群的秩就等于1。所以根据BSD猜想，如果猜想成立那么就有以下推论：L (E,1) = 0当且仅当椭圆曲线E有无穷个有理数解。

BSD猜想的解决和很多问题的解决都有重要联系，如著名的同余数问题：给定正整数n, 是否存在三条边都是有理数的直角三角形, 其面积恰好是n? 已经证明n是同余数等价于和它相关的椭圆曲线有无限多个有理数解。而椭圆曲线理论在解决费马猜想中也起到了关键作用。如果费马方程有整数解，那么这个解就满足一条椭圆曲线方程即费雷(Frey)曲线，而1990年里贝特(Ribet)证明该曲线不能是模曲线；然而谷山-志村猜想(Taniyama-Shimura conjecture)(怀尔斯1995年证明了该猜想)又可以推出任何费雷曲线都是模曲线，从而产生矛盾, 也就证明了费马方程无非平凡整数解。

然而，BSD猜想至今仍未得到解决，解析解给出的最好结果是r_an < 3，而采用代数方法计算群秩的道路也充满挑战，虽然有很多算法上的进展，但都不能给出群代数秩的确信计算结果，所以大多数数学家都认为，解决该问题需要提出新的想法和概念才能解决。证明BSD猜想还需大量的理论工作和创新的数学能力，如果它很容易的话，就不会被克雷研究所选择为价值一百万美元的千禧年七大数学问题之一了。