魔方：从几何到代数，从代数到几何

科学网—用48个魔方体会“魔方和Oh点群” - 李世春的博文

图1  U面上的置换三角形

         几年前，我根据这个三角形，就得到结论：魔方共有48个这样的置换三角形，操作序列都在{B2URL’B2LR’UB2}内，即48个操作序列都是9次操作，而且具有某种相关性。同时我认定，这48个操作序列的关系，满足Oh点群的某种代数关系。

         魔方魅力无穷，魔方的内涵已经溢出魔方本身。因此可以说，魔方既是几何的化身，魔方又是代数的化身。魔方既是生物表现型的化身，魔方又是生物基因型的化身。

         魔方的图案属于几何范畴，魔方的操作序列属于代数范畴。以此类推，数学只有两大分支：代数和几何。同理，生物界只有两样特性：表现型和基因型。表现型属于几何范畴，基因型属于代数范畴。例如，羞花闭月，沉鱼落雁，这是四大美人的表现型。她们之所以能羞花闭月和沉鱼落雁，就是因为她们的碱基的特殊排列组合，这是一个典型的代数问题，也就是四大美人的基因型。用魔方隐喻表现型和基因型，对应魔方图案和操作序列。魔方图案是几何，操作序列是代数。

         如图1所示，魔方的这个图案，是典型的几何问题。图中红色的边块置换三角形，就是用(B2URL’B2LR’UB2)操作出来的，因此，三角形是表现，是几何。而操作序列则是基因，是代数。不但如此，置换三角形和操作序列具有更深刻的几何和代数的关系。

        初步看，置换三角形在U面上，有4种分布形式：三角形可以转动90°、180°、270°，如果转360°，就和原来的重合了。因此，在U面上有4种分布，如果考虑到置换三角形的顺时针和逆时针方向，那么，在U面上的三角形总共有8种。我把这8种三角形放在一起，如图2所示，魔方的几何属性一目了然。

图2  U面上的8个置换三角形

         单从几何上考虑，在U面上的置换三角形，共有8种，也只有这8种。需要指出的是，图2中最上面的操作序列和红色符号标注，那是我后来做的。我最开始的时候，是仅仅从几何考虑问题的，U面上有8种三角形，魔方有6个面，应该共有48种情况。

         我用操作序列(B2URL’B2LR’UB2)，可以在U面上产生一个边块置换三角形。这是事实，也是100%的实践结论。在此基础上，我根据几何推论出：这样的边块置换三角形应该有48种，分布在魔方的6个面上，每面有8个。

         根据图1的三角形，或者说以图1 的三角形为起点，完全可以画出图2中的其他7个三角形，这就是几何问题，没有什么困难，谁都可以做到这一点。

（a）                             （b）                                （c）

图3 三边块置换的几何图像

        图1就是图3中的(a)，是序列(B2URL’B2LR’UB2)操作1次的结果；图3中的(b)，是序列(B2URL’B2LR’UB2)操作2次的结果；图3中的(c)，是序列(B2URL’B2LR’UB2)操作3次的结果。因此，我用(B2URL’B2LR’UB2)^3=I表示图3的操作结果，重写于下面

(B2URL’B2LR’UB2)^3=I                                          （1）

(B2URL’B2LR’UB2)(B2U’RL’B2LR’U’B2)=I           （2）

         表达式(1)描述的是一个Loop，相当于是一个轮回。表达式(2)描述的是魔方经过(B2URL’B2LR’UB2)操作后，没有继续向前走，而是按照序列(B2U’RL’B2LR’U’B2)退回来了。我这里用I表示对魔方的一种操作效果，相当于是没有操作。例如，F2F2=I，就是先转F面180°，然后再转F面180°，效果等于没有操作，因此表示为F2F2=I。同样，UU’=I，R’R=I，LL’=I，等等。我把表达式(2)中的括号去掉后重写于下，就是

B2URL’B2LR’UB2B2U’RL’B2LR’U’B2=I           （3）

B2URL’B2LR’UIU’RL’B2LR’U’B2=I                   （4）

        显然，在表达式(3)中，R’UIU’R=R’UU’R=R’IR=R’R=I，以此类推，最后表达式(4)成为I=I。

        因此，我把I称为单位操作序列，简称为单位序列，魔方经过单位序列操作后，和没有操作是一样的。对于点群，对应的概念是单位元素。例如，C4^2[100]C4^2[100]=e。e是点群操作的单位元素，如果选择点群的矩阵表示，e就是单位矩阵。显然，e和I绝对不是一回事。I用于操作序列的运算，e用于点群元素的运算。

        (B2URL’B2LR’UB2)^3=I表明，对魔方进行(B2URL’B2LR’UB2)操作，连续三次之后，等于对魔方没有任何影响的操作。这就是I的含义，描述的是一个轮回，对应的英文表示就是Loop。什么是循环呢？完成(B2URL’B2LR’UB2)一次，就是一次循环(Cycle)，循环3次，魔方回到出发前的状态。显然，Loop(轮回)比循环(Cycle)大，循环(Cycle)在轮回(Loop)之内。佛家也说轮回比春夏秋冬的循环大很多，为了数学地描述魔方，我用需要Loop和Cycle两个概念(变量)来描述魔方图案和操作序列的数学运算。

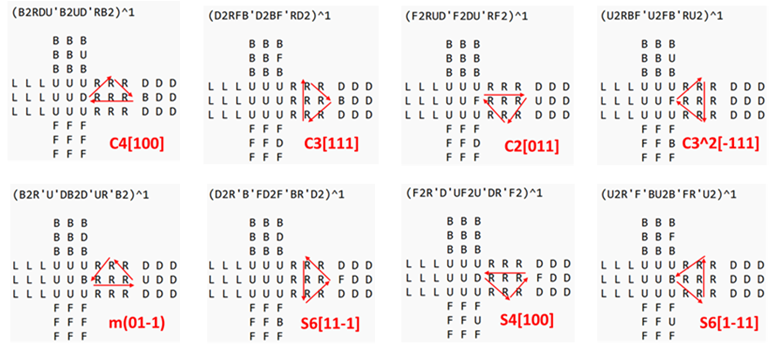
图4   R面上的8个置换三角形

         从图案到操作序列，就是从几何到代数的问题。如何把对应几何图案的操作序列推导出来，强有力的数学工具就是点群，点群就是经典的代数。可以验证，图4中所列出的8个操作序列，它们的Loop指数都是3，即它们的表达式都具有如下的格式

(B2RDU’B2UD’RB2)^3=I          (5)

         图4中的8个操作序列，都满足以上的代数关系。对比后，你会看出，图4中的8个操作序列，是各不相同的，因为图4中的几何图案各不相同，因此，产生这些图案，它们的操作序列也各不相同，因为几何图案和操作序列是一一对应的。图2给出了U面几何图案的操作8种操作序列，图4又给出了F面几何图案的8种操作序列，试试看，你能总结出什么规律，把剩下的32个操作序列归纳出来？

图5   F面上的8个置换三角形

图6   B面上的8个置换三角形

图7   L面上的8个置换三角形

图8   D面上的8个置换三角形

         以上列出了所有的48个边块置换三角形，操作序列为{ B2URL’B2LR’UB2}，包括48个具体的序列。如果说48个三角形是魔方几何，那么，48个序列就是魔方代数。

 U面代数：

(B2URL’B2LR’UB2)；(R2UFB’R2BF’UR2)；（F2ULR’F2RL’UF2)；(L2UBF’L2FB’UL2)；(B2U’L’RB2R’LU’B2)；(R2U’B’FR2F’BU’R2)；(F2U’R’LF2L’RU’F2)；(L2U’F’BL2B’FU’L2)

R面代数：

(B2RDU’B2UD’RB2)；(D2RFB’D2BF’RD2)；(F2RUD’F2DU’RF2)； (U2RBF’U2FB’RU2)；(B2R’U’DB2D’UR’B2)；(D2R’B’FD2F’BR’D2)； (F2R’D’UF2U’DR’F2)；(U2R’F’BU2B’FR’U2)

F面代数：

(U2FRL’U2LR’FU2)；(R2FDU’R2UD’FR2)；(D2FLR’D2RL’FD2)；(L2FUD’L2DU’FL2)；(U2F’L’RU2R’LF’U2)；(R2F’U’DR2D’UF’R2)；(D2F’R’LD2L’RF’D2)；(L2F’D’UL2U’DF’L2)

B面代数：

(D2BRL’D2LR’BD2)； (R2BUD’R2DU’BR2)；(U2BLR’U2RL’BU2)；(L2BDU’L2UD’BL2)； (D2B’L’RD2R’LB’D2)；(R2B’D’UR2U’DB’R2)；(U2B’R’LU2L’RB’U2)；(L2B’U’DL2D’UB’L2)

L面代数：

(B2LUD’B2DU’LB2)；(U2LFB’U2BF’LU2)； (F2LDU’F2UD’LF2)；(D2LBF’D2FB’LD2)；(B2L’D’UB2U’DL’B2)；(U2L’B’FU2F’BL’U2)；(F2L’U’DF2D’UL’F2) ；(D2L’F’BD2B’FL’D2)

D面代数：

(B2DLR’B2RL’DB2)；(L2DFB’L2BF’DL2)；(F2DRL’F2LR’DF2)；(R2DBF’R2FB’DR2)； (B2D’R’LB2L’RD’B2)；(L2D’B’FL2F’BD’L2)；(F2D’L’RF2R’LD’F2)； (R2D’F’BR2B’FD’R2)

          魔方代数，就是关于操作序列的运算，也就是关于UFRBLD排列组合的运算，就如同碱基排列组合一样，是一种DNA代数。因此，魔方是基因型和表现型的化身，魔方也是几何和代数的化身。

         未了更好地玩魔方，需要学点群论，正好我40年前就学过群论。

科学网—吉林大学之光：丁培柱的《群论》课 - 李世春的博文