Perspective: New models for multi-dimensional stable vortex solitons

 Hidetsugu Sakaguchi

Nonlinear Physics Laboratory, Department of Advanced Energy Science and Engineering, 
Kyushu University, Japan
 

Solitons are stable solitary waves. In 1834, Scott Russel first observed such a solitary water wave in a narrow channel near Edinburgh. In 1895, D. Korteweg and G. de Vries had derived the Korteweg-de Vries (KdV) equations for waves on shallow water surfaces. In 1965, N. Zabusky and M. Kruskal had demonstrated the stability of the solitary waves in the KdV equation using numerical simulations, and coined the term “soliton”. In 1967, Gardner, Greene, Kruskal, and Miura had discovered the mathematical technique of the inverse scattering transform to find analytical solutions to the KdV equation in a systematic manner, and the KdV equation was thus recognized as a paradigmatic integrable partial differential equation. The nonlinear Schrödinger (NLS) equation is another extremely important integrable system, which has a form of 

There are plane-wave solutions to this equation, however, the cubic self-focusing nonlinear term (with g < 0) causes modulational instability and creates solitary waves. The NLS equation can model gravity waves on the surface of deep inviscid water and light waves in various optical media, as well as many other physical media. A great many of papers and books about solitons have been published [1–3].

More recently, the nonlinear Schrödinger equation was applied to the Bose-Einstein condensates (BECs) of ultracold atoms. The cubic nonlinear term in the NLS equation comes from collisions between the ultra-cold atoms. In this case, g is positive and negative for repulsive and attractive interactions, respectively. Solitons were observed experimentally in Bose-Einstein condensates of ⁷Li atoms with attractive interactions [4, 5]. In the studies of Bose-Einstein condensates, external potentials are often used to confine BECs. The nonlinear Schrödinger equation with external potentials are called the Gross-Pitaevskii equation in this context.

The NLS equation in one dimension is an integrable system, which may be completely solved by the inverse scattering method. However, the two- or three-dimensional NLS equation is not integrable. There is a singular phenomenon called collapse in two- and three-dimensional NLS equations with cubic self-focusing nonlinearity, g <0 [6, 7]. In two dimensions, there is a critical value for the total norm,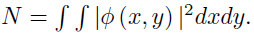 

If N is lower than the critical value, N_c , an initially localized state becomes delocalized under the action of the dispersion term, 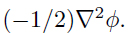 If N > N_c, the localized structure becomes progressively more localized and the peak amplitude of the localized structure diverges in a finite time, which is known as the collapse. In any case, it is known that there are no stable solitons in in two- and three-dimensional NLS equations with cubic nonlinearity.

However, there are several types of generalized NLS equations, which are not integrable systems but have stable multi-dimensional localized solutions. Such stable localized solutions are often called solitons, although some people use the term soliton only for localized solutions in integrable systems. In one type of generalized NLS equations, repulsive quintic nonlinearities or saturable nonlinearities are added [8, 9], while the standard NLS equation has only a self-focusing cubic nonlinearity. The higher-order nonlinearity weakens the self-focusing effect when the peak amplitude increases, and the collapse is suppressed.

A model equation of another type features a repulsive nonlinearity whose strength grows from the center to the periphery. In the standard NLS equation with the cubic self-defocusing nonlinearity, a uniform state is stable and a localized structure is hardly created. However, when the nonlinearity grows from the center toward the periphery at a rate faster than RD in the D-dimensional geometry, multi-dimensional solitons can be created [10–12]. In BECs, the nonlinearity can be controlled using the magnetic Feshbach resonance [13].

The other method for the stabilization of multidimensional uses the spin-orbit coupling (SOC) in binary BECs. SOC can be effectively introduced in BECs using Raman lasers [14]. Stable vortex solitons called semi-vortices and mixed-modes were found in numerical simulations of two-dimensional spin-orbit-coupled Gross-Pitaevskii equations, even if only the self-focusing cubic nonlinearity are included [15]. In semi-vortices, one component is a fundamental (zero-vorticity) soliton, and the other component carries the vorticity, while each component includes fundamental and vortical terms in the mixed modes. Furthermore, metastable vortex solitons were found in three dimensions [16].

Recently, Zhong et al. have proposed a new system, which includes both the repulsive nonlinearity, whose strength grows from the center to the periphery, and SOC [17]. Their NLS system for two components of mean-field wave functions,   has the form of 

where the coefficient λ represents SOC. They have found stable semi-vortex solitons and mixed-mode solitons by means of numerical simulations. In addition to the numerical results, exact analytical solutions were obtained for semi-vortex solitons at particular values of parameters in one and two dimensions. They have also found that semi-vortex states with higher vorticities, and higher-order mixed-mode solitons with necklace structures are numerically stable (see an example of the latter in the figure), while their counterparts found in previously studied models were completely unstable. Thus, new types of stable soliton have been found by Zhong et al. in the realm of generalized NLS equations in two dimensions.

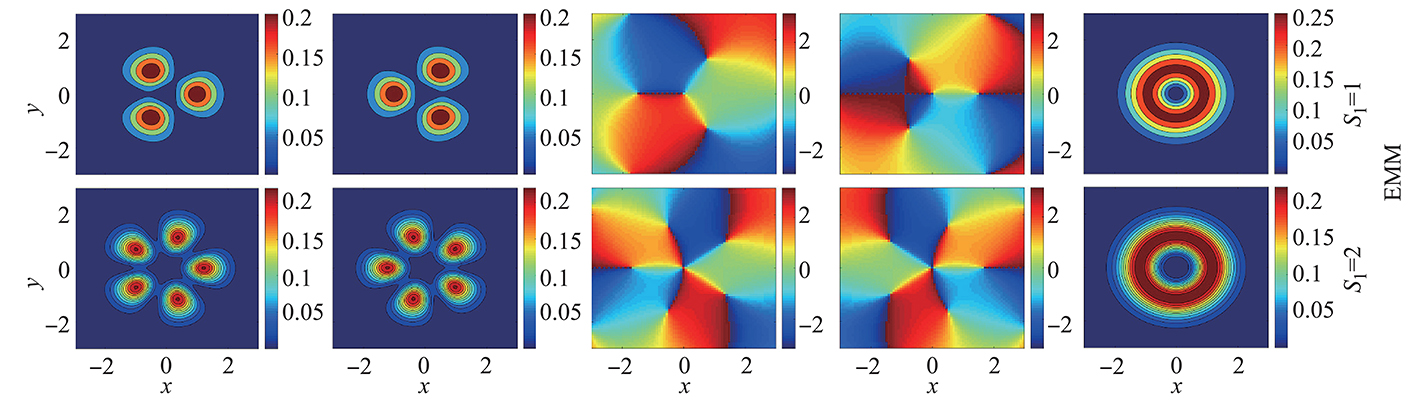
Fig. 1 The top and bottom panels display examples of stable higher-order mixed-mode states, with additional vorticities 1 and 2, respectively. Sets of two left panels, and two central ones, show, respectively, the distribution of densities of the two components, and their phases. The right panels display patterns of the total density,  in the same states, which remain axially uniform. The figure reproduces a part of Fig. 7 from the paper by Zhong et al. [17]. 

References

[1] M. J. Ablowitz and P. A. Clarkson, Solitons, Nonlinear Evolutions Equations, and Inverse Scattering, Cambridge University Press, New York, 1991

[2] G. L. Lamb Jr., Elements of Soliton Theory, Dover, New York, 1994)

[3] Y. S. Kivshar and G. P. Agrawal, Optical Solitons, Academic Press, San Diego, 2003

[4] K. E. Strecker, G. B. Partridge, A. G. Truscott, and R. G. Hulet, Formation and propagation of matter-wave soliton trains, Nature 417, 150 (2002)

[5] L. Khaykovich, F. Schreck, G. Ferrari, T. Bourdel. J. Cubizolles, L. D. Carr, Y. Castin, and G. Salomon, Formation of a matter-wave bright soliton, Science 296, 1290 (2002)

[6] L. Bergé, Wave collapse in physics and applications to light and plasma waves, Phys. Rep. 303, 259 (1998)

[7] G. Fibich and G. Papanicolaou, Self-focusing in perturbed and unperturbed nonlinear Schrödinger equation in critical dimension, SIAM J. Appl. Math. 60, 183 (1999)

[8] J. M. Soto-Crespo, D. R. Heartley, E. Wright, and N. N. Ahkmediev, Stability of the higher-bound states in a saturable self-focusing medium, Phys. Rev. A 44, 636 (1991)

[9] V. Skarka and V. I. Berezhiani, and R. Mijkaszewski, Spatiotemporal soliton propagation in saturating nonlinear optical media, Phys. Rev. E 56, 1080 (1997)

[10] O. V. Borovkova, Y. V. Kartashov, B. A. Malomed, and L. Toner, Algebraic bright and vortex solitons in defocusing media, Opt. Lett. 36, 3088 (2011)

[11] Q. Tian, L. Xie, H. Zhang, and J. F. Zhang, Vortex solitons in defocusing media with spatially inhomogeneous nonlinearity, Phys. Rev. E 85, 056603 (2012)

[12] R. Driben, Y. Kartashov, B. A. Malomed, T. Meier, and L. Toner, Three-dimensional hybrid vortex solitons, New J. Phys. 16, 063035 (2014)

[13] G. Roati, M. Zaccanti, C. D’Errico, J. Catani, M. Modugno, A. Simoni, M. Inguscio, and G. Modugno, ³⁹K Bose-Einstein condensate with tunable interactions, Phys. Rev. Lett. 99, 010403 (2007)

[14] Y. J. Lin, K. Jimenez-Garcia, and I. B. Spielman, Spin-orbit-coupled Bose-Einstein condensates, Nature 471, 83 (2011)

[15] H. Sakaguchi, B. Li, and B. A. Malomed, Creation of two-dimensional composite solitons in spin-orbit-coupled selfattractive Bose-Einstein condensates in free space, Phys. Rev. E 89, 032920 (2014)

[16] Y. C. Zhang, Z. W. Zhou, B. A. Malomed, and H. Pu, Stable solitons in three dimensional free space without the ground state: Self-trapped Bose-Einstein condensates with spin-orbit coupling, Phys. Rev. Lett. 115, 253902 (2015)

[17] R.-X. Zhong, Z.-P. Chen, C.-Q. Huang, Z.-H. Luo, H. S. Tan, B. A. Malomed, and Y.-Y. Li, Self-trapping under two-dimensional spin-orbit coupling and spatially growing repulsive nonlinearity, Front. Phys. 13, 130311 (2018)

文献链接

Hidetsugu Sakaguchi, New models for multi-dimensional stable vortex solitons, Front. Phys. 13, doi: 10.1007/s11467-018-0857-0