博文
读书笔记——易扩张C-Space中的路径规划
|||
本文作为论文Path Planning in Expansive Configuration Spaces的阅读笔记。
首先介绍一下该论文的整体思路:作者其实就是提出了一种单查询算法,而且为其做了理论证明,我甚至合理怀疑单查询算法就是发韧于这篇论文。具体来说,作者为了能够给出一个单查询路径规划方法,先为自由空间(free space)F定义了“易扩张性”概念;然后给出“连接序列”的概念,利用“易扩张性”证明“连接序列”最终能够以极大的概率在任意两个查询位姿之间找到路径;最后根据这个理论提出了一种单查询路径规划算法。
所谓完备规划器是指如果存在路径,则其必能找到,若不存在,则其必能指出。由于完备规划器搜寻路径的时间复杂度为指数级,因而人们开始逐渐关注随机规划器。RPP(Randomized Path Planner)是一种随机规划器,它沿着C-Space人工势场的负梯度方向搜索路径,并利用随机行走(random walks)脱离局部最小。但是,如果在脱离局部最小时必须穿过一个狭窄通道,RPP的表现就相当糟糕了,因为随机行走能够穿过狭窄通道的概率相当小。
PRM类规划器同样是随机的。不过它们当中有一些能够达到“概率完备”的水平,即如果存在路径,它几乎必能找到。不过,如果不存在,它很可能就没法终止了。
该论文给出了易扩张C-Space的概念,并且证明了如果在易扩张空间中用均匀采样的办法建立地图(roadmap),那么该地图的连通性与自由空间的连通性能够以很高的概率保持一致。也就是说,该论文的方法能够达到概率完备的水平。
在此论文提出以前,PRM都是多查询的,在整个C-Space采样,然后建立一张能够反映整个C-Space情况的地图。当然,这个地图是可以重复利用的,如果只用一次,显然太浪费了。而事实上,实际情况中有太多的“一次性”问题,我们叫它们单查询问题。你一定觉得在整个C-Space采样实在是没必要,因为那样会建立一张很大的地图,里面可能包含了很多连通分支,而对于两个查询位姿,即$q_{init}$和$q_{goal}$而言,只可能有一个连通分支将它们都包含在内,其他的连通分支对于此次单查询任务来说,统统没用。
于是,论文作者想要设计一种策略,使得它能够只在包含$q_{init}$ 和$q_{goal}$的连通分支上采样:首先在$q_{init}$或$q_{goal}$的临域内采样,然后在已经与$q_{init}$ 或$q_{goal}$建立连接的那些点的临域内采样,如此迭代,直到在$q_{init}$ 和$q_{goal}$找到路径。
下面给出几个定义:
对于任意$S\subseteq F$,$\mu \left (S \right )$表示S的体积,方便起见,假设$\mu \left (F \right )$=1。如果两个位姿能够用位于F中的直线连接,则称它们相互可见(visible)。$\nu \left (p \right )$表示点p在F中的可见区域,其中$p \in F$ 。
定义1:设$\alpha , \beta , \epsilon$是开区间(0, 1)之间的常数,则F是$\left (\alpha, \beta, \epsilon \right )$-易扩张的,如果F的任意一个连通分支$F^{'} \subseteq F$满足如下条件:
1.对于任意一个点$p \in F^{'}$,有$\mu \left (\nu \left (p \right ) \right ) \geq \epsilon$;
2.对于任意一个连通子集$S \subseteq F^{'}$,点集$LOOKOUT \left (S \right )=\left \{ q \in S \mid \mu \left (\nu \left (q \right ) \setminus S \right ) \geq \beta \times \mu \left (F^{'} \setminus S\right )\right \}$的体积满足$\mu \left (LOOKOUT \left (S \right ) \right ) \geq \alpha \times \mu \left (S \right )$。
解释一下这个定义。首先你要清楚,作者提出这个概念是为了后面利用它证明单查询方法的可行性。第一个条件很容易理解,即F中的每个点可以看见至少$\epsilon$部分的F。为了解释第二个条件,先看下面一张图:

可以发现,LOOKOUT是S的一个子集,这个子集满足一个条件,即其中的点所能看到S以外的部分的体积,占S关于其所在连通分支$F^{'}$的补集的比例不小于$\beta$。那么,第二个条件就是说,这个LOOKOUT的体积占整个S的比例不小于$\alpha$。
根据上述解释,如果一个自由空间F有较大的$\alpha$和$\beta$,则通过增加新的采样来扩张可见区域就是一件比较容易的事,因为在F的任一个连通分支$F^{'}$ 的子集S中,有相当一部分($\beta$ )的点具有辽阔($\alpha$ )的视野。我们将S看作是点集M所产生的可见区域,如果可以很容易地在S中找到一些点并添加到M中能够使M的可见区域,即S本身获得较大扩张,那么S最终会覆盖整个F,从而我们可以获取足够多的关于C-Space的信息来解决路径规划问题。
下面的两个图用于说明引入$alpha , beta , epsilon$的初衷。


上面两幅图反映了运动规划领域“臭名昭著”的窄道(narrow passage)问题。在窄道问题中,随机采样很难完整反映C-Space的连通性,原因在于找到一些能够连接窄道内的里程碑(milestones)并成功穿过窄道的路径实在太难了。如果对上面两幅图进行随机采样,得到的结果很可能是它们的两个半球被割开了,两个半球位于两个不同的连通分支上。用$alpha , beta , epsilon$对C-Space进行参数化是为了更好地捕捉C-Space的复杂结构,并且利用这些参数表示规划时间,进而通过改变这些参数来分析规划时间的变化。
上述两幅图的任一幅都不可能同时具有较大的$\alpha$和较大$\beta$ 。以右边的图为例,设它就是F中的某个连通分支$F^{'}$ ,它的左半球为S。如果想要S中的点在看右半球时有比较开阔的视野,即想要有较大的$\beta$ ,则这些点必须靠近两个半球相连的“开口”处,显然,这样的点仅仅是S中的少数,即$\alpha$较小。反之,如果想要$\alpha$较大,则$\beta$必然较小。
不过,上述两幅图也有不同的地方。左图,如果想要有较大的$\beta$,则$\alpha$较小,并且如果$\beta$足够大,$\alpha$一定等于0。从图上看,假设$beta = frac{1}{2}$,左半球中显然没有视野这么开阔的点,于是$alpha = 0$。然而,在右图中,无论$\beta$取多大(当然,不超过1),$alpha notequiv 0$。这是因为在两球的“开口”处,点的视野是足够开阔的,它的$\beta$ 能够无线趋近1。
下面给出一个概念,两个引理以及一个定理,用来从数学上证明作者用单查询方法构建的地图(其实只是经典PRM地图中很小的一块)的连通性能够以很高的概率与F的连通性保持一致。
定义2:点$p \in F$的连接序列(linking sequence)由一个点序列$p_{0} = p, p_{1}, p_{2}, \cdots $和一个点集序列$V_{0}=\nu \left (p_{0} \right ), V_{1}, V_{2}, \cdots \subseteq F$组成,且对于任意$i \geq 1$,有$p_{i} \in LOOKOUT \left (V_{i-1} \right )$且$V_{i}=V_{i-1} \cup \nu \left (p_{i} \right )$。
连接序列示意图如下:
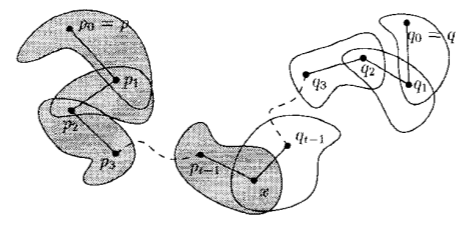
引理1:设M是从自由空间F中独立、均匀、随机地选出的具有n个里程碑的点集。令$s=1/ \alpha \epsilon$。给定任意点$p \in M$,M中存在一个长度为t的p的连接序列的概率至少为$1-se^{- \left (n-t-1 \right )/s}$。
引理2:设$v_{t}=\mu \left (V_{t} \right )$表示由点$p \in F^{'}$ 的连接序列$p_{0}, p_{1}, p_{2},\cdots $ 确定的第t个点集$V_{t}$的体积,其中$F^{'}$是F的一个连通分支,则对于$t \geq \beta^{-1} \ln 4 \approx 1.39/ \beta$,有$v_{t} \geq 3 \mu \left (F^{'} \right )/4$。
设S是一个从F中采样得到的里程碑集合,R是一个地图,它由S以及在S中所有相互可见的两个里程碑之间加入边构成,$M \subseteq S$ 。对于F的任意连通分支$F^{'}$ ,令$M_{j} \subseteq M$ 是$F_{j}$ 中里程碑的集合,$R_{j}$ 是包含了$M_{j}$ 中顶点的R的子图。
定理3:设$\gamma \in \left (0,1 \right )$为常数,点集S中的2n个点是从自由空间F中独立、均匀、随机地选出,其中$n=\left \lceil 8\ln \left (8/\epsilon \alpha \gamma \right )/\epsilon \alpha +3/\beta +2\right \rceil$。那么,每个$R_{j}$是连通图的概率至少为$1-\gamma$。
这些引理和定理的证明在此略过。简单说一下这些定理的意义。引理1说明,对于任意一个通过在自由空间F中随机采样得到的里程碑集合,它包含一个给定长度t的、位于该里程碑集合中的任一点p的连接序列的概率还是相当大的。引理2说明,这个给定长度为t的连接序列的体积能够扩张很大。对于任意的两个里程碑p和q,它们各自的连接序列不断膨胀的结果就是最后一定会相交。这时,p和q之间就能用一条路径连接起来了。定理3估计了$R_{j}$ 是连通图的概率,而且可以看出n越大,$\gamma$ 就越小,$R_{j}$ 是连通图的概率就越大。
其实上面的定义、定理很容易把人搞糊涂,因为一会是F,一会又是F的连通分支$F^{'}$ ,乱七八糟,难以看清定理的真正用途。但是,请别忘了,该论文就是想要提出一种单查询方法,这种方法最终只建立一个连通分支。所以,当你看到“对于每一个F的连通分支$F^{'}$”这样的话时,直接认为$F^{'}$就是F即可!
下面终于要将前面的理论用于算法设计的实践中了!
如果$q_{init}$ 连接序列的可见区域和$q_{goal}$ 连接序列的可见区域相交,那么一条路径就被找到了。于是,算法的整体思路就有了:给定两个查询位姿$q_{init}$ 和$q_{goal}$ ,在C-Space中采样,但是只保留那些与$q_{init}$ 和$q_{goal}$有路径相通的位姿点。这样,分别以$q_{init}$ 和$q_{goal}$ 为根建立两棵树,两棵树不断生长,直到它们的可见区域相交,这时便能找到一条连接$q_{init}$ 和$q_{goal}$ 的路径。
算法分为两个步骤,即expansion和connection。由于以$q_{init}$ 为根,或以$q_{goal}$ 生长过程是一样的,不妨设任一棵树$T= \left (V,E \right )$ 。expansion具体步骤如下:

其中,$w \left (x \right )$ 表示权重。由步骤1可见,$w \left (x \right )$ 和选择x的概率成反比。这里,$w \left (x \right )$ 定义为T上位于$N_{d} \left (x \right )$ 内的采样点数目。可见,邻域点稀少的点能够以更高的概率获得在其周围采样的机会,这个算法有“损有余而补不足”之功效,即自适应,这样的好处是树上的点在最终形成的包含$q_{init}$ 和$q_{goal}$ 连通分支上均匀分布。$clearance:C \rightarrow R$ 将一个位姿q映射为该位姿下机器人与障碍物的距离。$link \left (x, y \right )$ 可以确定x和y之间是否存在一条直线路径。定义邻域的距离d的选取十分重要:若d选得太大,则很多采样点会落入与当前查询无关的连通分支中(试想,d选那么大,很可能在q和x之间有障碍物,那么在connection调用link函数时会发现它们无法用直线路径连接,于是q和x只好在不同的连通分支上了),这就犯了和经典PRM一样的毛病;若d选得太小,则大部分采样点分别集中在$q_{init}$ 和$q_{goal}$ 周围,两个查询位姿连接序列的可见区域不易相交,从而不易找到路径。关于K的选取,论文中指出它对算法影响不大,选10个就ok。
注意,clearance的实现有两种极端情况,一个是精确计算出机器人和障碍物之间的欧式距离,一个是退化为一个碰撞检测器,只返回YES或NO。该论文选择了前者,原因就在于link函数。link用于检测两个位姿p和q之间是否存在直线路径,它会不停地调用clearance。现假设clearance可以精确计算距离,且p和q的clearance分别为$\zeta$ 和$\eta$ 。定义p和q是相邻的(adjacent),如果$dist_{w} \left (p,q \right )<max \left (\zeta,\eta \right )$。如果p和q是相邻的,那么它们之间就存在一条直线路径。给定p和q,link迭代地将p和q之间的直线分割成很多小段,若这些小段的端点都是逐个相邻的,那么p和q之间就存在直线路径,否则就不存在。如果clearance不计算距离而只是充当碰撞检测器,那么link必须不停地分割p和q之间的直线,直到达到给定的分辨率为止,但是这样做往往会调用更多次的clearance(试想,若clearance可以计算距离,那么一旦检测到此时所有小段的端点逐个相邻,分割线段的工作就停止了;如果clearance不能计算距离,只好继续苦逼地分割下去),而且会十分依赖这个给定的分辨率。
connection具体步骤如下:
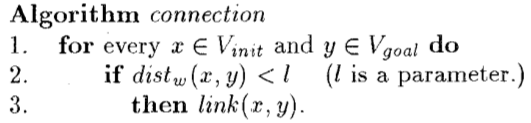
connection算法很容易理解,但是有一点需要注意,即此处的$dist_{w}$和expansion中的$dist_{c}$。前者应该反映出两位姿点越近,相互可见的可能性就越大,于是定义为当机器人沿着p和q之间的直线路径运动时,机器人身上所有点走过的最远距离。后者简单定义为两位姿点p和q在笛卡尔坐标系中的距离。
如果两个查询位姿之间不存在路径,那么规划器就会不停地运行下去。为了防止这一点,必须给出终止条件。可以限定expansion和connection的最大执行次数,也可以当两棵树上所有点的最小权值超过一定值后停止,因为这意味着我们的采样已经相当充分了。
实验部分和总结部分略过。
https://wap.sciencenet.cn/blog-795645-626780.html
上一篇:读书笔记——SBL,一种单查询、双向、延迟碰撞检测的PRM
下一篇:读书笔记——Lazy PRM
首先介绍一下该论文的整体思路:作者其实就是提出了一种单查询算法,而且为其做了理论证明,我甚至合理怀疑单查询算法就是发韧于这篇论文。具体来说,作者为了能够给出一个单查询路径规划方法,先为自由空间(free space)F定义了“易扩张性”概念;然后给出“连接序列”的概念,利用“易扩张性”证明“连接序列”最终能够以极大的概率在任意两个查询位姿之间找到路径;最后根据这个理论提出了一种单查询路径规划算法。
所谓完备规划器是指如果存在路径,则其必能找到,若不存在,则其必能指出。由于完备规划器搜寻路径的时间复杂度为指数级,因而人们开始逐渐关注随机规划器。RPP(Randomized Path Planner)是一种随机规划器,它沿着C-Space人工势场的负梯度方向搜索路径,并利用随机行走(random walks)脱离局部最小。但是,如果在脱离局部最小时必须穿过一个狭窄通道,RPP的表现就相当糟糕了,因为随机行走能够穿过狭窄通道的概率相当小。
PRM类规划器同样是随机的。不过它们当中有一些能够达到“概率完备”的水平,即如果存在路径,它几乎必能找到。不过,如果不存在,它很可能就没法终止了。
该论文给出了易扩张C-Space的概念,并且证明了如果在易扩张空间中用均匀采样的办法建立地图(roadmap),那么该地图的连通性与自由空间的连通性能够以很高的概率保持一致。也就是说,该论文的方法能够达到概率完备的水平。
在此论文提出以前,PRM都是多查询的,在整个C-Space采样,然后建立一张能够反映整个C-Space情况的地图。当然,这个地图是可以重复利用的,如果只用一次,显然太浪费了。而事实上,实际情况中有太多的“一次性”问题,我们叫它们单查询问题。你一定觉得在整个C-Space采样实在是没必要,因为那样会建立一张很大的地图,里面可能包含了很多连通分支,而对于两个查询位姿,即$q_{init}$和$q_{goal}$而言,只可能有一个连通分支将它们都包含在内,其他的连通分支对于此次单查询任务来说,统统没用。
于是,论文作者想要设计一种策略,使得它能够只在包含$q_{init}$ 和$q_{goal}$的连通分支上采样:首先在$q_{init}$或$q_{goal}$的临域内采样,然后在已经与$q_{init}$ 或$q_{goal}$建立连接的那些点的临域内采样,如此迭代,直到在$q_{init}$ 和$q_{goal}$找到路径。
下面给出几个定义:
对于任意$S\subseteq F$,$\mu \left (S \right )$表示S的体积,方便起见,假设$\mu \left (F \right )$=1。如果两个位姿能够用位于F中的直线连接,则称它们相互可见(visible)。$\nu \left (p \right )$表示点p在F中的可见区域,其中$p \in F$ 。
定义1:设$\alpha , \beta , \epsilon$是开区间(0, 1)之间的常数,则F是$\left (\alpha, \beta, \epsilon \right )$-易扩张的,如果F的任意一个连通分支$F^{'} \subseteq F$满足如下条件:
1.对于任意一个点$p \in F^{'}$,有$\mu \left (\nu \left (p \right ) \right ) \geq \epsilon$;
2.对于任意一个连通子集$S \subseteq F^{'}$,点集$LOOKOUT \left (S \right )=\left \{ q \in S \mid \mu \left (\nu \left (q \right ) \setminus S \right ) \geq \beta \times \mu \left (F^{'} \setminus S\right )\right \}$的体积满足$\mu \left (LOOKOUT \left (S \right ) \right ) \geq \alpha \times \mu \left (S \right )$。
解释一下这个定义。首先你要清楚,作者提出这个概念是为了后面利用它证明单查询方法的可行性。第一个条件很容易理解,即F中的每个点可以看见至少$\epsilon$部分的F。为了解释第二个条件,先看下面一张图:

可以发现,LOOKOUT是S的一个子集,这个子集满足一个条件,即其中的点所能看到S以外的部分的体积,占S关于其所在连通分支$F^{'}$的补集的比例不小于$\beta$。那么,第二个条件就是说,这个LOOKOUT的体积占整个S的比例不小于$\alpha$。
根据上述解释,如果一个自由空间F有较大的$\alpha$和$\beta$,则通过增加新的采样来扩张可见区域就是一件比较容易的事,因为在F的任一个连通分支$F^{'}$ 的子集S中,有相当一部分($\beta$ )的点具有辽阔($\alpha$ )的视野。我们将S看作是点集M所产生的可见区域,如果可以很容易地在S中找到一些点并添加到M中能够使M的可见区域,即S本身获得较大扩张,那么S最终会覆盖整个F,从而我们可以获取足够多的关于C-Space的信息来解决路径规划问题。
下面的两个图用于说明引入$alpha , beta , epsilon$的初衷。


上面两幅图反映了运动规划领域“臭名昭著”的窄道(narrow passage)问题。在窄道问题中,随机采样很难完整反映C-Space的连通性,原因在于找到一些能够连接窄道内的里程碑(milestones)并成功穿过窄道的路径实在太难了。如果对上面两幅图进行随机采样,得到的结果很可能是它们的两个半球被割开了,两个半球位于两个不同的连通分支上。用$alpha , beta , epsilon$对C-Space进行参数化是为了更好地捕捉C-Space的复杂结构,并且利用这些参数表示规划时间,进而通过改变这些参数来分析规划时间的变化。
上述两幅图的任一幅都不可能同时具有较大的$\alpha$和较大$\beta$ 。以右边的图为例,设它就是F中的某个连通分支$F^{'}$ ,它的左半球为S。如果想要S中的点在看右半球时有比较开阔的视野,即想要有较大的$\beta$ ,则这些点必须靠近两个半球相连的“开口”处,显然,这样的点仅仅是S中的少数,即$\alpha$较小。反之,如果想要$\alpha$较大,则$\beta$必然较小。
不过,上述两幅图也有不同的地方。左图,如果想要有较大的$\beta$,则$\alpha$较小,并且如果$\beta$足够大,$\alpha$一定等于0。从图上看,假设$beta = frac{1}{2}$,左半球中显然没有视野这么开阔的点,于是$alpha = 0$。然而,在右图中,无论$\beta$取多大(当然,不超过1),$alpha notequiv 0$。这是因为在两球的“开口”处,点的视野是足够开阔的,它的$\beta$ 能够无线趋近1。
下面给出一个概念,两个引理以及一个定理,用来从数学上证明作者用单查询方法构建的地图(其实只是经典PRM地图中很小的一块)的连通性能够以很高的概率与F的连通性保持一致。
定义2:点$p \in F$的连接序列(linking sequence)由一个点序列$p_{0} = p, p_{1}, p_{2}, \cdots $和一个点集序列$V_{0}=\nu \left (p_{0} \right ), V_{1}, V_{2}, \cdots \subseteq F$组成,且对于任意$i \geq 1$,有$p_{i} \in LOOKOUT \left (V_{i-1} \right )$且$V_{i}=V_{i-1} \cup \nu \left (p_{i} \right )$。
连接序列示意图如下:

引理1:设M是从自由空间F中独立、均匀、随机地选出的具有n个里程碑的点集。令$s=1/ \alpha \epsilon$。给定任意点$p \in M$,M中存在一个长度为t的p的连接序列的概率至少为$1-se^{- \left (n-t-1 \right )/s}$。
引理2:设$v_{t}=\mu \left (V_{t} \right )$表示由点$p \in F^{'}$ 的连接序列$p_{0}, p_{1}, p_{2},\cdots $ 确定的第t个点集$V_{t}$的体积,其中$F^{'}$是F的一个连通分支,则对于$t \geq \beta^{-1} \ln 4 \approx 1.39/ \beta$,有$v_{t} \geq 3 \mu \left (F^{'} \right )/4$。
设S是一个从F中采样得到的里程碑集合,R是一个地图,它由S以及在S中所有相互可见的两个里程碑之间加入边构成,$M \subseteq S$ 。对于F的任意连通分支$F^{'}$ ,令$M_{j} \subseteq M$ 是$F_{j}$ 中里程碑的集合,$R_{j}$ 是包含了$M_{j}$ 中顶点的R的子图。
定理3:设$\gamma \in \left (0,1 \right )$为常数,点集S中的2n个点是从自由空间F中独立、均匀、随机地选出,其中$n=\left \lceil 8\ln \left (8/\epsilon \alpha \gamma \right )/\epsilon \alpha +3/\beta +2\right \rceil$。那么,每个$R_{j}$是连通图的概率至少为$1-\gamma$。
这些引理和定理的证明在此略过。简单说一下这些定理的意义。引理1说明,对于任意一个通过在自由空间F中随机采样得到的里程碑集合,它包含一个给定长度t的、位于该里程碑集合中的任一点p的连接序列的概率还是相当大的。引理2说明,这个给定长度为t的连接序列的体积能够扩张很大。对于任意的两个里程碑p和q,它们各自的连接序列不断膨胀的结果就是最后一定会相交。这时,p和q之间就能用一条路径连接起来了。定理3估计了$R_{j}$ 是连通图的概率,而且可以看出n越大,$\gamma$ 就越小,$R_{j}$ 是连通图的概率就越大。
其实上面的定义、定理很容易把人搞糊涂,因为一会是F,一会又是F的连通分支$F^{'}$ ,乱七八糟,难以看清定理的真正用途。但是,请别忘了,该论文就是想要提出一种单查询方法,这种方法最终只建立一个连通分支。所以,当你看到“对于每一个F的连通分支$F^{'}$”这样的话时,直接认为$F^{'}$就是F即可!
下面终于要将前面的理论用于算法设计的实践中了!
如果$q_{init}$ 连接序列的可见区域和$q_{goal}$ 连接序列的可见区域相交,那么一条路径就被找到了。于是,算法的整体思路就有了:给定两个查询位姿$q_{init}$ 和$q_{goal}$ ,在C-Space中采样,但是只保留那些与$q_{init}$ 和$q_{goal}$有路径相通的位姿点。这样,分别以$q_{init}$ 和$q_{goal}$ 为根建立两棵树,两棵树不断生长,直到它们的可见区域相交,这时便能找到一条连接$q_{init}$ 和$q_{goal}$ 的路径。
算法分为两个步骤,即expansion和connection。由于以$q_{init}$ 为根,或以$q_{goal}$ 生长过程是一样的,不妨设任一棵树$T= \left (V,E \right )$ 。expansion具体步骤如下:

其中,$w \left (x \right )$ 表示权重。由步骤1可见,$w \left (x \right )$ 和选择x的概率成反比。这里,$w \left (x \right )$ 定义为T上位于$N_{d} \left (x \right )$ 内的采样点数目。可见,邻域点稀少的点能够以更高的概率获得在其周围采样的机会,这个算法有“损有余而补不足”之功效,即自适应,这样的好处是树上的点在最终形成的包含$q_{init}$ 和$q_{goal}$ 连通分支上均匀分布。$clearance:C \rightarrow R$ 将一个位姿q映射为该位姿下机器人与障碍物的距离。$link \left (x, y \right )$ 可以确定x和y之间是否存在一条直线路径。定义邻域的距离d的选取十分重要:若d选得太大,则很多采样点会落入与当前查询无关的连通分支中(试想,d选那么大,很可能在q和x之间有障碍物,那么在connection调用link函数时会发现它们无法用直线路径连接,于是q和x只好在不同的连通分支上了),这就犯了和经典PRM一样的毛病;若d选得太小,则大部分采样点分别集中在$q_{init}$ 和$q_{goal}$ 周围,两个查询位姿连接序列的可见区域不易相交,从而不易找到路径。关于K的选取,论文中指出它对算法影响不大,选10个就ok。
注意,clearance的实现有两种极端情况,一个是精确计算出机器人和障碍物之间的欧式距离,一个是退化为一个碰撞检测器,只返回YES或NO。该论文选择了前者,原因就在于link函数。link用于检测两个位姿p和q之间是否存在直线路径,它会不停地调用clearance。现假设clearance可以精确计算距离,且p和q的clearance分别为$\zeta$ 和$\eta$ 。定义p和q是相邻的(adjacent),如果$dist_{w} \left (p,q \right )<max \left (\zeta,\eta \right )$。如果p和q是相邻的,那么它们之间就存在一条直线路径。给定p和q,link迭代地将p和q之间的直线分割成很多小段,若这些小段的端点都是逐个相邻的,那么p和q之间就存在直线路径,否则就不存在。如果clearance不计算距离而只是充当碰撞检测器,那么link必须不停地分割p和q之间的直线,直到达到给定的分辨率为止,但是这样做往往会调用更多次的clearance(试想,若clearance可以计算距离,那么一旦检测到此时所有小段的端点逐个相邻,分割线段的工作就停止了;如果clearance不能计算距离,只好继续苦逼地分割下去),而且会十分依赖这个给定的分辨率。
connection具体步骤如下:
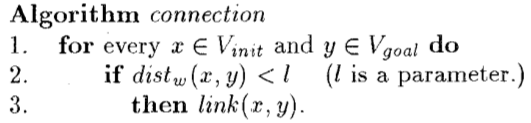
connection算法很容易理解,但是有一点需要注意,即此处的$dist_{w}$和expansion中的$dist_{c}$。前者应该反映出两位姿点越近,相互可见的可能性就越大,于是定义为当机器人沿着p和q之间的直线路径运动时,机器人身上所有点走过的最远距离。后者简单定义为两位姿点p和q在笛卡尔坐标系中的距离。
如果两个查询位姿之间不存在路径,那么规划器就会不停地运行下去。为了防止这一点,必须给出终止条件。可以限定expansion和connection的最大执行次数,也可以当两棵树上所有点的最小权值超过一定值后停止,因为这意味着我们的采样已经相当充分了。
实验部分和总结部分略过。
https://wap.sciencenet.cn/blog-795645-626780.html
上一篇:读书笔记——SBL,一种单查询、双向、延迟碰撞检测的PRM
下一篇:读书笔记——Lazy PRM
扫一扫,分享此博文
全部作者的其他最新博文
全部精选博文导读
相关博文
- • 700年后日本或濒临灭绝?日本学者推算预测:届时或仅剩1名15岁以下孩子
- • [转载]【同位素视角】非英语母语学者如何区分’e.g.’, ‘i.e.’, ‘namely’与‘such as’等混淆难题
- • 美国佐治亚大学等机构学者:刈割策略对Bulldog 805紫花苜蓿+Tifton 85狗牙根混播草地产量及品质的影响
- • 美国堪萨斯州立大学、密苏里大学等机构学者研究成果:土壤水分管理策略和品种多样性对紫花苜蓿产量、营养品质和农场盈利能力的影
- • 德国、捷克草业科学学者长期放牧实验:异质草地斑块中的土壤有机碳储量和地下生物量
- • 如何才能连续被评为十年“中国高被引学者”?——对话上海大学王卿文教授