博文
强相关逻辑及其应用(上)
||
[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容,请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处,恕本人在网上广泛公布侵权者姓名。敬请各位读者注意,谢谢!
强相关逻辑及其应用(上)
程京德
[注:本文为笔者2016年发表在科技导报第34卷第7号上的文章“相关推论与强相关逻辑”(迄今为止唯一的一篇关于强相关逻辑的中文文献)之修改增补版,更换标题为“强相关逻辑及其应用”,发表在此。]
概要: 推理的能力,尤其是抽象推理的能力,无疑是人类智能最本质的特征之一,因而应该是任何以实现人工通用智能为目标的人工智能系统都应该提供的必不可少的最基本功能。本文介绍构建强相关逻辑的动机,展示强相关逻辑的各种应用,并且指出,为相关推理提供逻辑有效性保证的强相关逻辑,对于以推理、发现、预测为最基本功能的各种人工智能系统来说,具有无可替代的关键作用。强相关逻辑是实现人工通用智能不可或缺的逻辑基础。
何谓“推理”?何谓“证明”?
首先,让我们先来澄清两个经常被混淆的不同概念,“推理”和“证明”。为此,我们还需要先说明什么是论证(argument)/论断(inference)。
论证(argument)/论断(inference)是从若干个前提得出一个结论的步骤。比较形式地说,论证/论断是一个陈述(statement)的集合,其中一个为该论证/论断的结论,其它则为前提,论证/论断的前提为其结论提供证据。
推理(reasoning)是从给定前提(premises)(亦即,为结论提供证据的已知事实或预设假说)推导出新结论(new conclusion)的过程,是从已知或预设(亦即,前提)到达未知(亦即,新结论)从而扩展已有知识、获取新知识的认知过程。一个推理过程一般是由一系列论证/论断的步骤有序地构成的。
我们所掌握的知识,尤其是抽象知识,并非都是由我们自己亲身经历过后从直接的经验总结得出的,大部分都是根据已知知识通过推理而间接地得到的。可以说,如果没有推理这一认知手段,我们就不可能把人类的知识宝库扩展到今天这样如此丰富的地步。
我们来看一个用自然语言表达的推理的简单实例。
(1)若一个数是有理数,则它一定可以被表达为一对整数之比。
(2)π不能被表达为一对整数之比。
所以
(3)π不是一个有理数。
(4)π是一个数。
所以
(5)至少存在一个非有理数(无理数)。
这里,我们用一步论证先从前提(1)和(2)得出(3)作为结论,又用一步论证从前提(3)和(4)得出(5)作为结论,这样的两步论证构成一个完整的推理,从前提(1),(2)和(4)推出结论(5)。
推理的前提应该为推理的结论提供相关的证据。但是,尽管推理的前提旨在为推理的结论提供相关的证据,但它们实际上未必真的做到了这样。所以,我们把真正提供了相关证据的推理认定为是对的/正确的推理,而把没有真正提供了相关证据的推理认定为是错误的/不正确的推理。那么,谁为这种正确性提供判别标准呢?是逻辑学!
另一方面,推理的结论针对其前提应该是新的结论。我们把真正获得了新结论的推理认定为是有效的推理,而把没有真正获得了新结论的推理认定为是无效的推理。那么,谁为这种有效性提供判别标准呢?还是逻辑学!但是,到目前为止,如何形式地且令人满意地定义“新”这一概念仍然是一个棘手的哲学问题。
推理的能力,尤其是抽象的概念推理的能力(除去人类,其它动物并不具备这种能力),无疑是人类智能最本质的特征之一,因而应该是任何以实现人工通用智能为目标的人工智能系统都应该提供的必不可少的功能。
证明(proving)是从给定前提为一个明确规定的陈述(explicitly specified statement)寻找正当理由(justification)的过程,这些前提是已知事实或预设假设,它们为该明确规定的陈述提供证据。一个证明过程一般是由一系列论证/论断的步骤有序地构成的,将此有序过程具体描述出来,就构成一个证明描述(proof)。
我们来看一个用自然语言表达的证明的简单实例,证明:π是一个无理数。
(1)若一个数是有理数,则它一定可以被表达为一对整数之比。
(2)π不能被表达为一对整数之比。
所以
(3)π不是一个有理数。
(4)凡不是有理数的数都是无理数。
所以
(5)π是一个无理数。
这里,我们用一步论证先从前提(1)和(2)得出(3)作为结论,又用一步论证从前提(3)和(4)得出需要证明的(5)作为结论,这样的两步论证构成一个完整的证明,从前提(1),(2)和(4)证明了结论(5)。
证明的前提应该为证明的明确规定陈述提供相关的证据。但是,尽管证明的前提旨在为证明的明确规定陈述提供相关的证据,但它们实际上未必真的做到了这样。所以,我们把真正提供了相关证据的证明认定为是对的/正确的证明,而把没有真正提供了相关证据的证明认定为是错误的/不正确的证明。那么,谁为这种正确性提供判别标准呢?还是逻辑学!
推理和证明之间最本质的区别在于,前者本质上是规范性/规定性和预测性的,而后者本质上是描述性和非预测性的。推理的目的是找到一些以前未知或未被识别的新结论,而证明的目的是为一些以前已知或假设的某些陈述找到正当理由。证明有一个明确规定的陈述作为其目标,而推理则没有。
典型的推理模式为:从A,B,C,…,我们能说什么?在推理结束之前,我们并不知道从这些前提到底能够得出什么新结论。
典型的证明模式为:从A,B,C,…,我们能说 D 吗?在证明结束之前,我们确切地知道我们必须从前提出发证明什么陈述是对的。
何谓逻辑学?
在上述有关论证/论断、推理、证明的一般定义中,尽管我们说前提要为结论提供相关的证据,但是一个具体论证/论断、推理、证明的前提是否实际上真正有效地为其结论提供了相关的证据是独立于一般定义的另一件事,也就是说,确实提供了或者实际上没有提供都是可能的。因此,我们就需要某种确切的标准来区分和鉴别正确的、有效的论证、推理、证明和不正确的、非有效的论证、推理、证明。逻辑学正是研究论证和推理的正确性或有效性的学问学科。
“逻辑学是一门研究论证与推理之正确性的基础性学问,其目的为建立和建全用于判断各种论证与推理之正确性的一般标准。”[1]
逻辑学首先是关于论证与推理的学问,它探索和研究究竟是什么构成了正确的、有效的论证与推理,探索和研究用于区分鉴别正确的、有效的论证与推理和不正确的、非有效的论证与推理的一般原理和标准,探索和研究如何进行正确的、有效的论证与推理而避免不正确的、非有效的论证与推理的一般方法论。因此,历史上,逻辑学从来就被称之为“科学之科学,技艺之技艺”(司各脱,13世纪)、“所有其它科学之基础”(塔斯基,1941)、“先于所有其它科学,以其思想和原理支撑所有科学之科学”(哥德尔,1944)。
另一方面,在各种各样论证与推理的前提和结论之间可以有多种不同种类的证据关系存在,而对不同的证据关系的认同与否就可以引导出不同的正确性有效性标准。任何科学都是基于一些基本假设和基本原理建立起来的,一旦其中某个假设或原理被一个新的假设或原理所替换,可能会给予该门科学巨大影响,以至于创生出一个全新的分支。逻辑学也不例外,关于基本假设和基本原理的不同哲学动机可以引导出不同的逻辑有效性标准和不同的逻辑系统。一般地说,尽管任何逻辑学家的研究对象都应该是论证与推理及其正确性,但是不同的逻辑学家出自不同的哲学观点,对建立怎样的用于判断各种论证与推理之正确性的一般逻辑有效性标准会有不同的看法和方案,因此就会建立起不同的逻辑有效性标准,导致不同的逻辑系统。
作为逻辑学之核心的条件句
关于什么是逻辑学中最核心的概念,如同逻辑学的定义一样,至今仍然是一个有争论的话题。许多逻辑学家(尤其是相关逻辑学家)认为,“条件句”是逻辑学中的最核心概念。
在自然语言中以“如果(若,if)…,那么(则,then)…”形式出现的句子,在逻辑学中通常被称为“条件命题(conditional proposition)”或简单地被称为“条件句(conditional)”。一个条件句意图断定,在条件句的“如果”部分(逻辑学中称为“前件(antecedent)”)和“那么”部分(在逻辑学中称为“后件(consequent)”)之间,存在着一种必然相关的充分条件关系:亦即,如果前件成立的话,那么后件也应该成立。
条件句在所有(没有例外)的文学、社会科学、逻辑学、数学、自然科学、工程技术、我们人类日常生活言谈中都起到必不可少、不可或缺的基本作用。文学家在作品中用条件句来描写各种推理场景;逻辑学家、数学家、科学家或工程师在各种概念定义、命题、定理、规则的陈述中用条件句来表达概念、事实、断定、结论与它们的前提之间的充分条件关系。
从逻辑学的角度来说,条件句的必不可少、不可或缺是因为它出现在任何一种论证形式(演绎、归纳、溯因)当中,而各种形式的论证是我们人类所有文化活动中所必须的。 所以,条件句概念在历史上一直都是逻辑学研究中最重要的课题,从而被认为是逻辑学的核心 [2]。既然“条件句”概念如此重要和不可或缺,当然需要在学术上把它定义清楚。那么,如何清晰准确地定义“条件句”概念?这其实仍然是一个还没有完全解决的难题。
历史上最早讨论“条件句”概念是古希腊哲学家第奥多鲁斯·克诺鲁斯(Diodorus Cronus)和他的学生麦加拉的菲罗(Philo of Megara)[3]。塞克斯都·恩披里柯(Sextus Empiricus)在提及这场讨论时列举了四种关于条件句性质的观点:“(1)菲罗说,完善的条件句是一种不是开始于真而结束于假的条件句。… (2)第奥多鲁斯说,完善的条件句是一种即非过去可能,又非现在可能开始于真而结束于假的条件句。… (3)那些采用联系概念的人说,一个条件句当它的后件的矛盾句是和它的前件不相容时就是完善的条件句。… (4)那些用蕴涵关系来判断的人说,一个真的条件句是其后件潜在地包含在前件里面的条件句。”[3]。
“当菲罗说一个条件句是完善的,当且仅当它不是开始于真而结束于假,他就是在提供一个“如果。。。那么。。。”的现在所谓的真值函项定义,也就是说,按照这样一种定义,条件陈述句的真或假是由它的前件和后件的真假所决定的。”[3] 经典数理逻辑里的真值函数联结词“实质蕴涵(material implication)”,其定义便是起源于菲罗的定义,所以也有逻辑学家称其为“菲罗蕴涵”。
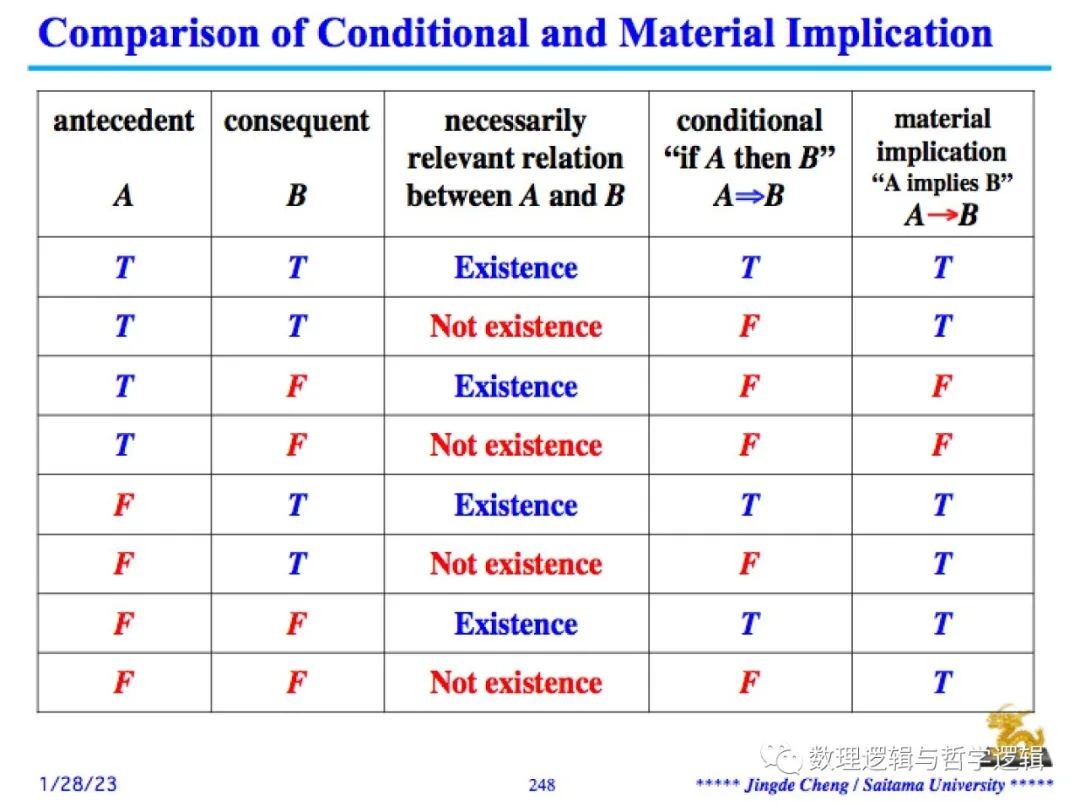
经典数理逻辑里的真值函数联结词“实质蕴涵”(这里用“->”来表达,定义为:A->B =df not(A and notB) 或者 A->B =df notA or B)并非条件句的恰如其分的准确表达。下面的表显示了条件句与实质蕴涵的一个真值表比较。从表中我们可以看出,条件句的真假不仅仅取决于其前件后件的真假,还取决于其前件后件之间有无必然相关关系;而实质蕴涵的真假仅仅取决于其前件后件的真假,与其前件后件之间有无必然相关关系毫不相干。相对于前件后件的真假组合,条件句显示出“三真四假”的真值结果,而实质蕴涵仅仅显示出“三真一假”的真值结果。这个真值表比较十分清楚地显示出条件句与实质蕴涵在逻辑语义上的不同,用实质蕴涵来表达条件句是不准确的、有问题的。
逻辑学界把用实质蕴涵来表达条件句时所产生的问题统称为“(实质)蕴涵悖论(paradoxes of material implication, implicational paradoxes)”问题[2-6]。
比如,下面这些经验条件句命题(经验蕴涵悖论,从常识来看明显不能被认为真的)如果用实质蕴涵来表达,那么按照实质蕴涵的逻辑语义都应该是真的:
“如果雪是白的,那么1+1=2” 表达为 “雪是白的->1+1=2”
“如果雪是黑的,那么1+1=2” 表达为 “雪是黑的->1+1=2”
“如果雪是黑的,那么1+1=3” 表达为 “雪是黑的->1+1=3”
而下面这些条件句命题(逻辑蕴涵悖论)则都是经典数理逻辑的逻辑定理:
A->(B->A),
B->(notA or A),
notA->(A->B),
(notA and A)->B (ECQ, ex contradictione quodlibet),
(A->B) or (notA->B),
(A->B) or (A->notB),
(A->B) or (B->A),
((A and B)->C)->((A->C) or (B->C))
从应用的角度来看,对于基于经典数理逻辑的任何应用,如果你有任意两个命题p和q使得 not(p and notq) 或者 notp or q 为真,那么你必须无条件地接受p->q作为一个真“条件句”,即便p和q之间没有任何相关性,因为这是经典数理逻辑的规则。这种情形对于类似自动定理证明的应用来说可能会引来效率低下问题,但是对于类似自动定理发现的应用来说却是一个致命的缺陷。
对于用“菲罗蕴涵”来表达条件句,在古希腊时代就有反对和争议。当形式逻辑被完全形式化为经典数理逻辑,实质蕴涵被用作为其真值函数联结词(在有些经典数理逻辑形式化系统中还被定义为初始联结词)之后,许多逻辑学家对于(实质)蕴涵悖论问题就不能容忍了。下面我们仅介绍一些对该问题的解决有本质上进展的工作。
美国逻辑学家刘易斯(Clarence Irving Lewis)是现代模态逻辑的创始人,但其实他的工作的最初目的就是改造经典数理逻辑里的实质蕴涵,试图找到一个可以替代实质蕴涵的新逻辑联结词来更准确地表达条件句[4-6]。刘易斯认为实质蕴涵没有表达出条件句中的必然性,因此引入了表达必然性的模态算子□来定义用来表达条件句的蕴涵关系,称为严格蕴涵(strict implication)(这里用“-3”来表达): A-3B =df □(A->B),并且构造了相应的模态逻辑系统S1,S2,S3,S4,S5。但是,在刘易斯的几个模态逻辑系统的逻辑定理当中,仍然遗留了一些“严格蕴涵悖论(paradoxes of strict implication)”[4-6]:
□A->(B-3A) [相当于经典数理逻辑中的 A->(B->A)]
□notA->(A-3B) [相当于经典数理逻辑中的 notA->(A->B)]
(notA and A)-3B [相当于经典数理逻辑中的 (notA and A)->B]
B-3(notA or A) [相当于经典数理逻辑中的 B->(notA or A)]
刘易斯模态逻辑中的严格蕴涵悖论,(notA and A)-3B 和 B-3(notA or A),和经典数理逻辑中的实质蕴涵悖论,(notA and A)->B 和 B->(notA or A),以完全相同的形式出现,故而被一些逻辑学家称为最典型最难排除的蕴涵悖论。请注意一点,在这两个蕴涵悖论中,蕴涵之前件与后件之间可以不共享任何命题变量,因此可以是绝对毫不相干的。
1956年,德国逻辑学家阿克曼(Wilhelm Ackermann)指出,用一个外延真值函数联结词来表达条件句是有问题的,应该用一个初始内涵联结词来表达条件句[7],这在逻辑学史上是一个极其具有革新性的思想,也是相关逻辑这个领域的发端[2]。阿克曼提出一个新的内涵逻辑联结词,称为“Strengen Implikation(rigorous implication,严密蕴涵)”(这里用“=>”来表达),用其来表达条件句,并且说到,“Rigorous implication, which we write as A=>B, should express the fact that a logical connection holds between A and B, that the content of B is part of that of A, or however one wishes to express it. That has nothing to do with the truth of falsity of A or B. Thus one would reject the validity of the formula A=>(B=>A), since it permits the inference from A of BTA, and since the truth of A has nothing to do with whether a logical connection holds between B and A.”[2,6,7]。阿克曼提出的对表达条件句的初始内涵逻辑联结词的思想,后又被 von Wright,Geach,Smiley 三位逻辑学家分别归纳和陈述,现在被称为“The von-Wright-Geach-Smiley criterion for entailment”,简称“WGS criterion”,是关于条件句表达的重要标准[2]。
阿克曼构筑了Strengen Implikation 的形式逻辑系统 π',这是逻辑学史上第一个完整的相关逻辑系统。π’从其逻辑定理中成功地完全排除了实质蕴涵悖论和严格蕴涵悖论[2,7]。
美国逻辑学家安德森(Alan Ross Anderson)和贝尔纳普(Nuel Dinsmore Belnap, Jr.)以及他们的学生们从上世纪五十年代到七十年代在相关逻辑领域做了一系列的工作。他们提出了初始内涵联接词“必然归结(entailment)”的概念,并且将阿克曼的相关逻辑 π’重构为等价的相关逻辑系统“system E of entailment”,提出了初始内涵联接词“相关蕴涵(relevant implication)”的概念并构造了相关逻辑系统“system R of relevant implication”(以及其它一些相关逻辑系统)[2]。这些相关逻辑系统都从其逻辑定理中成功地完全排除了实质蕴涵悖论和严格蕴涵悖论[2]。
各个相关逻辑系统完全排除实质蕴涵悖论和严格蕴涵悖论的理论保证源于“相关性原理(The relevance principle)”:一个条件句形式相关逻辑定理的前件后件之间必须共享至少一个命题变量。相关性原理在形式上保证了在相关逻辑中恒真条件句命题的前件后件之间的必然相关性,这是所有相关逻辑系统必然满足的本质特征[2]。正是因为所有相关逻辑系统的逻辑定理都必然地满足相关性原理,其条件句形式逻辑定理的前件后件之间都共享至少一个命题变量,所以,那些前件后件之间毫不相关的、被称之为最典型最难排除的蕴涵悖论就都全部被从相关逻辑系统逻辑定理中排除掉了。
然而,是否严密蕴涵、必然归结、相关蕴涵已经完美地准确表达了充分条件关系,相关性原理已经完美地限制了所有的蕴涵悖论,传统的相关逻辑已经彻底终结了条件句表达这一难题了呢?笔者通过自己的研究工作给出了否定的回答。
由于相关性原理仅仅要求在一个条件句形式相关逻辑定理的前件后件之间必须共享至少一个命题变量,它仅仅保证了该条件句的前件后件之间的必然相关,却没有保证前件中的所有成分与后件中的所有成分都必然相关。
让我们来考虑下面几个例子:
(A and B)=>A,
(A and B and …)=>A,
(A and B)=>B,
(A and B and …)=>B,
(A and B)=>((A and C)=>B),
(A and B)=>((A and C and …)=>B)
这些条件句命题都是相关逻辑的逻辑定理(可以看出,它们都满足相关性原理),因此把具体命题代入其命题变量都应该得到(在相关逻辑系统内的)真命题。但是,在这些逻辑定理的前件中都包含有与后件不相关的合取項。比如,把具体命题“雪是白的”,“1+1=2”,“1+1=3”代入命题变量A,B,C,那么会得到:
(雪是白的 and 1+1=2)=>雪是白的,
(雪是白的 and 1+1=2 and …)=>雪是白的,
(雪是白的 and 1+1=2)=>1+1=2,
(雪是白的 and 1+1=2 and …)=>1+1=2,
(雪是白的=>1+1=2)=>((雪是白的 and 1+1=3) =>1+1=2),
(雪是白的=>1+1=2)=>((雪是白的 and 1+1=3 and …)=>1+1=2)
显然,如果把上面这些例子中的相关的蕴涵联结词“=>”都视为充分条件关系“如果…,那么…”,那么得到的条件句在含义上就很怪异可笑了,因为按照通常的常识和经验来看,这些条件句的前件和后件里有一部分毫不相干,甚至即便某些成分是假命题也无妨。
让我们再考虑下面几个例子:
A=>(A or B),
A=>(A or B or …),
B=>(A or B),
B=>(A or B or …),
(A=>B)=>(A=>(B or C)),
(A=>B)=>(A=>(B or C or …))
这些条件句命题也都是相关逻辑的逻辑定理(可以看出,它们都满足相关性原理),因此把具体命题代入其命题变量也都应该得到(在相关逻辑系统内的)真命题。但是,在这些逻辑定理的后件中都包含有与前件不相关的析取项。如果把具体命题“雪是白的”,“1+1=2”,“1+1=3”代入命题变量A,B,C,也会得到类似于上面在含义上很怪异可笑的条件句。
从这些实例可以看出,尽管传统相关逻辑已经排除了那些传统的蕴涵悖论,但是在它们的逻辑定理集合当中也还仍然存在着一些条件句形式逻辑定理,从我们通常使用充分条件关系的意义来看是不自然的、怪异可笑的。如果将传统相关逻辑中的相关蕴涵联结词就视为是充分条件关系,而把相关逻辑中的逻辑定理都视为有效的推理形式,那么从正确推理的角度来看,传统相关逻辑的许多逻辑定理仍然表现出类似于“实质/严格蕴涵悖论”的特性。这一情形,与把经典数理/模态逻辑中的“实质/严格蕴含”视为是充分条件关系,而把经典数理/模态逻辑中的逻辑定理都视为有效的推理形式时所产生的“实质/严格蕴含悖论”问题完全类似。这个事实揭示了尽管“相关蕴涵”比“实质/严格蕴涵”更恰当地表达了充分条件关系概念,但是类似于“实质/严格蕴涵”的情形,“相关蕴涵”也还没有完美地准确表达充分条件关系。
笔者于上世纪90年代前期命名相关逻辑的上述那些有问题的逻辑定理为“合取蕴涵悖论(conjunction-implicational paradox)”和“析取蕴涵悖论(disjunction-implicational paradox)”,因为在一个合取蕴涵悖论条件句的前件中包含有不必要的、不需要的、不相干合取项,或者在一个析取蕴涵悖论条件句的后件中包含有不必要的、不需要的、不相干析取项,或者两者皆而有之。为了建立起能够支持相关推理的条件句逻辑演算,笔者提出了排除合取蕴含悖论和析取蕴含悖论的强相关逻辑(strong relevant logic, strong relevance logic)系统。强相关逻辑要求,对于每一个表示有效的推理形式的条件句来说,其前件中不得包含不必要的、不需要的、不相干合取项,并且其后件中不得包含不必要的、不需要的、不相干析取项。强相关逻辑在相关逻辑满足相关性原理的基础上,进一步满足“强相关性原理(The strong relevance principle)”:条件句形式逻辑定理中的每一个命题变量必须作为前件成分和后件成分各出现至少一次。作为传统相关逻辑的改良,强相关逻辑排除了传统相关逻辑中的合取蕴含悖论和析取蕴含悖论,使得在一个基于满足强相关性原理的强相关逻辑的有效推理之前提中不会出现与其结论无关的合取项,结论中也不会出现与其前提无关的析取项[8-11]。
那么,在强相关逻辑的逻辑定理当中,是否还存在从条件句正确表达来看仍有问题的某种“悖论”呢?对于这个问题,目前还没有定论。
相关逻辑学家认为,“‘条件句’ 概念是逻辑学中的核心(We take the heart of logic to lie in the notion ‘if … then …’)”[2]; “现代逻辑学中的问题可以最好地表述为:我们能否对那些表达必然归结关系的条件句给出解释?(The problem in modern logic can best be put as follows: can we give an explanation of those conditionals that represent an entailment relation)”[12]。显然,如果我们把条件句视为逻辑学的最核心概念,那么条件句概念的清晰准确定义无疑就是逻辑学中最重要的课题。这个难题,到今天还未完全解决。
(未完待续)
参考文献
[1] 程京德, “逻辑学是什么?” 微信公众号“数理逻辑与哲学逻辑”,2023年1月25日。
[2] R. Anderson, and N. D. Belnap Jr., Entailment, “The Logic of Relevance and Necessity,” Vol. I, Princeton University Press, Princeton, 1975.
[3] W. Kneale and M. Kneale, “The Development of Logic,” Oxford Clarendon Press, 1962, 1984 (Paperback Edition with Corrections); 中译:张家龙,洪汉鼎 译 “逻辑学的发展”,商务印书馆, 1985.
[4] 王宪钧, “数理逻辑引论”,北京大学出版社,1982, 1998.
[5] S. Read, “Relevant Logic: A Philosophical Examination of Inference,” Basil Blackwell, Oxford, 1988, 2012.
[6] L. Haaparanta (Ed.), “The Development of Modern Logic,” Oxford University Press, 2009.
[7] W. Ackermann, “Begrundung Einer Strengen Implikation,” The Journal of Symbolic Logic, Vol. 21, pp. 113-128, 1956 (in German).
[8] J. Cheng, “Rc - A Relevant Logic for Conditional Relation Representation and Reasoning,” Proceedings of the 1st Singapore International Conference on Intelligent Systems, pp. 171-176, Singapore, September 1992.
[9] J. Cheng, “A Relevant Logic Approach to Automated Theorem Finding,” Proceedings of the Workshop on Automated Theorem Proving attached to International Symposium on Fifth Generation Computer Systems 1994, pp. 8-15, Tokyo, Japan, December 1994.
[10] J. Cheng, “Entailment Calculus as the Logical Basis of Automated Theorem Finding in Scientific Discovery,” in “Systematic Methods of Scientific Discovery: Papers from the 1995 Spring Symposium,” AAAI Technical Report SS-95-03, pp. 105-110, AAAI Press, March 1995.
[11] J. Cheng, “A Strong Relevant Logic Model of Epistemic Processes in Scientific Discovery,” in “Information Modeling and Knowledge Bases XI,” Frontiers in Artificial Intelligence and Applications, Vol. 61, pp. 136-159, IOS Press, February 2000.
[12] M. R. Diaz, “Topics in the Logic of Relevance,” Philosophia Verlag, München, 1981.
微信公众号“数理逻辑与哲学逻辑”
https://wap.sciencenet.cn/blog-2371919-1392136.html
上一篇:“PM及相关系统的形式不可判定命题”(2)- 哥德尔不完全性定理的涵义及有效范围
下一篇:《相关逻辑与人工智能》教学大纲 The Syllabus of “Relevant Logic and AI”