第十八章 多隐层结构的非显性特征

18.1 隐层黑箱

一、向量空间的特征基

在深度学习多隐层模式出现之前，人工智能的主要理论基础是“向量”。 以向量作为分析工具是自然而然的想法，因为任何分析都要参照系，大家最熟悉的可量化的参照系就是坐标系（比如笛卡尔坐标系），而坐标系中以向量为分析对象容易实现。

下面以语义识别为例，我们来看看如何对自然语言向量化。自然语言一个显著特点是，不同词汇之间可以相互表达。比如:

国王＝男人＋权势＋财富

王后＝女人＋权势＋财富

并且，词汇之间的这种表达是互相可换的，比如：

权势男人＝ 国王＋财富

一般而言，我们把等式右边的词汇叫做‘基础词汇’（特征基）。虽然基础词汇是相对的，但是选取恰如其分基础词汇可以大大简化语义表达。也就是说，选取恰如其分基础词汇是的自然语言向量化关键第一步。那么应该选取哪些词汇作为特征基呢？目前最简单实用的方法是“稀疏编码”（Sparse Coding）。通过一个重复迭代的过程，找到最广泛的使用频率最高的那些词汇，作为基础词汇。

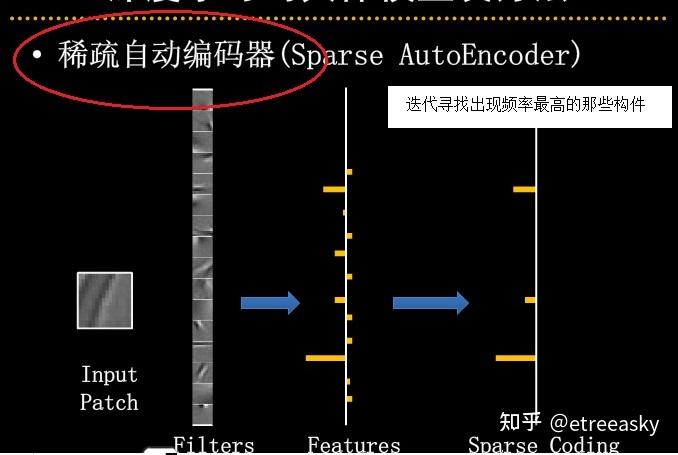
有了基础词汇（特征基），即是建立了参照系的坐标轴。

然后，是把需要分析的词汇‘投影’到坐标轴（基础词汇）。比如‘国王’和‘宰相’都是有权势有财富的男人，如何区分这两个词汇呢？以投影权重很容易精确表达这两个词的含义，比如：

国王＝1.0×男人＋1.0×权势＋0.9×财富

宰相＝1.0×男人＋0.9×权势＋0.8×财富

这种以线性空间量化表达自然语言的方法就叫做语言向量化。当然，实际语言环境下‘基础词汇 ’不仅仅是性别、权势、财富三维，很可能需要n维才能准确表达广泛话题。（需要注意的是，基础词汇越多，能够表达的特征信息就会越多，表达的准确度就越高，语义内涵会越细腻；另一方面，基础词汇多，则计算复杂度会大大增加，系统识别响应可能严重迟缓。所以基础词汇并非越多越好，需要在精确度和响应时间之间找一个平衡。） 在普遍意义下，我们可以定义一个函数W ，W可以把任意单词按照其语义映射为一个高维向量。

W:words→Rn

比如，

W(“cat”)=(0.2, -0.4, 0.7, …)

其中，(0.2, -0.4, 0.7, …) 表示在特征属性向量空间中“猫”的语义投影值

W(“mat”)=(0.0, 0.6, -0.1, …)

其中，(0.0, 0.6, -0.1, …) 表示在特征属性向量空间中“垫子”的语义投影值

总而言之，这个W函数就是一个查询表，用一个矩阵θ来参数化，每行是一个单词的某个子属性投影：Wθ(wn)=θn

单词向量化展示了一个更引人注目的属性：单词间的类比性（即数学的内积），度量了词与词之间的关系。向量内积关系的作用一目了然，这对于语义分析至关重要。 这种单词构成的“地图”对我们来说更直观。相似的词会离得近，这看起来是很自然的事。相似的单词距离近，能让机器系统分析变得容易，比如从一个句子演变出一类相似的句子。 这不仅指把一个词替换成一个它的同义词，而且指把一个词换成一个相似类别里面的词（如“the wall is blue” → “the wall is red” ）。进一步地，我们可以替换多个单词（例如“the wall is blue” → “the ceiling is red”）。它的影响对单词数目来说是指数级的 。很可能很多情况下它是先知道“the wall is blue”这样的句子是成立的，然后才见到“the wall is red”这样的句子。这样的话，把“red”往”blue”那边挪近一点，网络的效果就更好。

向量空间不仅仅量化了词汇、量化了词与词之间的关系、还有效量化了词与词的组合（句子），所以机器系统能分析句子的语义。进而，器系统能分析整段话题，甚至能分析归纳出整遍文章的主题。

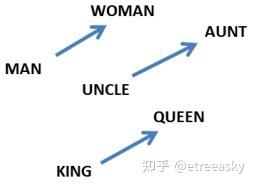
以向量空间特征基作为人工智能语义识别的逻辑参照系模型很早就有了，比如“支持向量机”技术，向量空间逻辑模型在小范围小样本空间分析中取得了一定成效。但是在普遍语言环境范围中，即使增添了很多技巧，“支持向量机”认知能力仍然非常有限，存在明显的局限性。对于这种分析局限性，一般的解释是，广泛普遍语言环境下的高维词汇向量需要的维度比较大，造成机器计算量非常巨大，n维空间往往需要2的n次方的指数级运算量，现阶段计算机硬件不足，实现较为困难。在普通程序员眼中，计算量是直观的感受，所有困顿自然而然地来自于计算量。我们必须清醒的是，向量空间（单层线性空间）的局限性，本质是由于“不完备性定理”，而不仅仅是运算量的复杂度。

　　数字化、数学化、向量化，是形式化语言基本思想。 百年以前，哥德尔的奇思妙想，也是把自然语言数字化、把自然语言公理化、把自然语言向量化，这与早期机器学习的过程如出一辙。但是，哥德尔以严密数学理论，论证了形式化自然语言向量空间化固有的、本质的、根本的、永恒的、绝对的、不可辩驳的局限性。它不是运算量的局限性，而是参照系架构的局限性。形式化自然语言是一阶逻辑，其线性演算轨迹的参照系是向量空间。

二、隐层的特征基

令人瞠目结舌的是，最近几年“深度学习”人工智能模型居然在广泛的普遍的语言范围中很好的完成了语义识别，显示的能力远远超越了“支持向量机”，超越了自然语言向量化技术的局限性，超越了形式逻辑公理化的局限性，超越了线性空间局限性。那么“深度学习”模型又是凭什么实现的超越呢？ 既然一阶逻辑图灵机永远都不可能超越具有多层次化思维能力的人脑，“深度学习”模型又有什么逻辑神器敢与多层次化生物神经网络一决高下呢？

深度学习模型的突破在于其多隐层架构，在于其多层次的“子特征结构”参照系。

由于基本线性结构类似，初学者容易混淆向量和张量的概念，特别是在有限维的情况下。在有限维的情况下，张量空间的数学定义一般是这样的：

(φ+ψ)(x) =φ(x)+ψ(x)

(aφ)(x)=aφ(x)

上式可以化成下面的一个式子：

(φ+ψ)(ax+by) =aφ(x)+aψ(x)+bφ(y)+bψ(y)

初学者容易混淆：如果把φ(x)、ψ(x)、φ(y)、ψ(y)各看成基矢量，这不就是一个向量空间吗？

其实不然！因为向量空间（平面矩阵）是单层次线性空间，逻辑结构图如下：

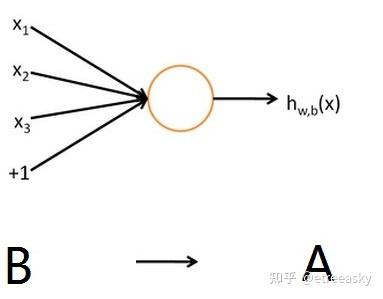
而(φ+ψ)(ax+by)构造的是双线性映射（二重线性映射）。并且我们还可以构造更复杂的三重（即三阶）线性映射：（F+g)(φ+ψ)(ax+by)。 更高阶张量其链接线条的逻辑结构比单层次的向量空间要复杂得多：

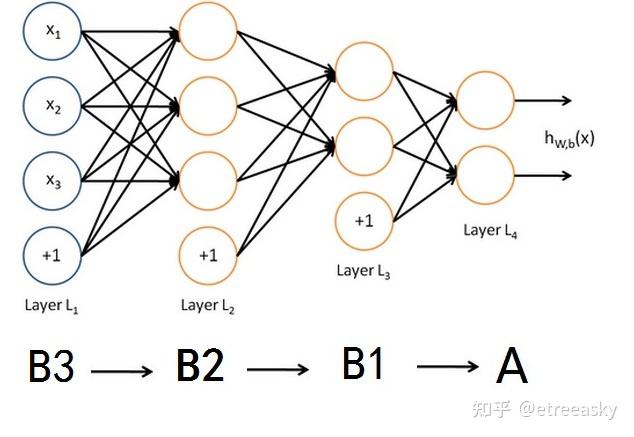
请注意，“（F+g)(φ+ψ)(ax+by) ”的三重线性映射的复合结构，包含了多重子线性结构 ，分别是（F+g)、(φ+ψ)和(ax+by)，它们分别表达了三个不同的偏线性空间。（F+g)是一个线性空间，(φ+ψ)是另一个线性空间，(ax+by）又是另外一个线性空间。

我们关心的问题是，有没有一种更高层次的统一参照系，能同时包含表达各种子结构系统呢？ 一般而言，“系统”可看作“集合+结构”。 当一个系综（张量）由多个系统而成时，则这个集合由多个‘子集合’组成，同时包含了多个‘子结构’。比如，一个细胞看作细胞核、核糖体、细胞质、内质网、高尔基体、囊泡、溶酶体、线粒体、细胞骨架、细胞膜、中心粒等等子集合；同时放大镜下，细胞中包含了不同子结构，这些子结构各不相同。有时候，不同子结构需要不同的子特征参照系，以各自不同的特色方式表达。

深度学习的特征提取具有层次化特点，不同层次的特征值有不同特性：①浅层特征捕捉基础模式，- CNN中：边缘、纹理、颜色等低级特征； - RNN中：单词、短语等基本语言单位。②中层特征组合基础特征， - CNN中：物体部件、形状等中等抽象特征；- RNN中：语义短语、句法结构。③ 深层特征高级抽象表示，- CNN中：完整物体、场景等高级特征；- RNN中：文本主题、情感等语义表示。

很多同学误会认为隐层的多层次特征是人为预先设定的，比如底层是边缘线条特征基、然后上一层是眼耳口鼻等子特征基、再上一层的是各年龄性别人种的脸谱特征基。

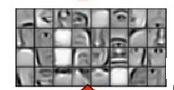
然而事实并非如此，深度学习隐层的特征基并不是训练前人为预先定义设定的，而是机器训练中自已动态生成的。深度学习各隐层权重参数集合找不到眼耳口鼻等子特征、也找不到各年龄性别人种的脸谱特征，深度学习各隐层的“非显性子特征”特征基是机器自己赋予的，其特征属性脱离我们惯常认知，对人类而言宛若“黑箱”。

在传统机器学习中，特征工程（Feature Eng∈eer∈g）是模型性能的关键瓶颈。需要依赖领域专家的知识，通过人工设计、选择和提取特征（如图像的SIFT特征、文本的TF-IDF特征），再将特征输入模型训练。这种方式不仅费时费力，而且特征的优劣直接决定了模型的性能，难以适应复杂数据（如图像、语音）的高维、非线性特性。

而深度学习彻底改变了这一模式，通过多层神经网络的结构，模型能够直接从原始数据（如图像的像素值、文本的字符序列）中自动学习特征。无需人工干预，模型会在训练过程中动态调整神经元之间的连接权重，逐层提取从低级到高级的特征，最终形成能够准确描述数据的内在特征表示。层级结构特征从简单到复杂、从具体到抽象逐层形成，这就是深度学习的“深度”的含义。

1. 输入层到隐层的线性变换：对于输入层（第0层）的特征向量fx^(0) （如图像的像素值、文本的Embedd∈g向量），其与隐层（第1层）的连接权重矩阵fW^(1) （尺寸为 D_1 × D_0 ， D_0 为输入特征维度， D_1 为隐层神经元数量）相乘，加上偏置向量fb^(1) ，得到隐层的加权输入（Pre-activation）： fz^(1) = fW^(1) . fx^(0) + fb^(1)，其中 fz^(1) 是隐层神经元的“原始输入”，尚未经过非线性变换。

这一层的权重矩阵 W 定义了特征基。计算 z = W * x + b。这个操作的本质是将输入 x 投影到 W 的每一行（每个基向量）所代表的方向上，得到一个中间向量 z。z 的每个元素 z_i 就代表了输入 x 与第 i 个特征基的匹配程度（点积结果）。

2. 非线性激活生成特征值：为了让模型学习到数据的非线性特征（如图像中的边缘、纹理），隐层的加权输入会通过激活函数（如ReLU、Sigmoid、Tanh）进行非线性变换，得到隐层的特征值集（Activation Values）： fa^(1) = f(fz^(1)) = f(fW^(1) . fx^(0) + fb^(1))，这里的fa^(1) 即为隐层（特征基）的特征值集，每个元素对应一个隐层神经元的输出，代表了输入数据在该神经元上的“响应强度”。

对 z 施加非线性激活函数a = ReLU(z)。得到的向量 a 的每个元素 a_i，就是该神经元最终的输出激活值，也就是我们通常所说的特征值。

3. 多层特征提取：上述过程会从输入层开始，逐层传递到更深层的隐层（如第2层、第3层），每一层的特征值集均由前一层的特征值集与当前层的权重参数集通过线性变换+激活函数生成。例如，第2层的特征值集fa^(2) 由第1层的特征值集fa^(1) 与第2层的权重矩阵fW^(2) 生成：fa^(2) = f(fW^(2) . fa^(1) + fb^(2))，随着层数加深，特征值集会逐渐从低级特征（如图像的边缘、纹理）过渡到高级特征（如图像中的物体部件、文本的语义），最终形成能够准确描述数据的特征基。

通过执行一次前向传播，将输入数据传递给网络。数据流经每一层时，都会与该层的权重（特征基）进行线性匹配，再经过非线性“淬炼”，最终输出该层的激活值（特征值）。这些激活值，就是该输入在当前网络所定义的特征空间中的具体坐标。

对于第 l 层的第 j 个神经元，有：

a_j^[l] = g( z_j^[l] ) = g( ∑ (w_ji^[l] * a_i^[l-1]) + b_j^[l] )

w_ji^[l]是权重参数，连接第 l-1 层第 i 个神经元和第 l 层第 j 个神经元，它定义了第 j 个特征基如何看待前一层第 i 个特征的重要性。 a_i^[l-1]是前一层的特征值， a_j^[l]是本层新生成的特征值。

这个公式清晰地表明：新特征值 a_j^[l] 是旧特征值 a_i^[l-1] 的加权和（权重为 w_ji^[l]），再经非线性变换 g 而来。

深度学习的特征基是通过训练动态生成的，而非人为预先定义。深度学习的各隐层特征基的均为隐式存在，无人工定义的具体表征规则。人类工程师仅仅是为深度学习AI搭特征基的“架子”，机器从数据中填特征基的“内容”，最终形成适配任务的隐式特征基体系。特征基的核心是权重矩阵（卷积核、词嵌入矩阵、Q/K/V权重），其权重值完全由机器从数据中自动学习，无人工定义任何特征提取规则（如人工指定“边缘特征是像素差为5的水平像素”）；人为仅定超参数仅设定特征基载体的规格（卷积核数量/大小、嵌入维度、注意力头数），这些是模型的“结构超参数”，而非特征基本身，目的是限定特征基的表征维度和学习范围，避免模型过拟合/欠拟合；学习的核心驱动力均通过“前向传播生成特征响应→反向传播计算梯度→梯度下降更新权重”的闭环，让特征基不断适配训练数据的真实模式，最终实现“特征基对输入的精准表征”。神经网络自动学习，在深度神经网络里，尤其是像卷积神经网络（CNN）、循环神经网络（RNN）及其变体（如LSTM、GRU）、Transformer 架构等，特征基通常靠模型在训练时自动学习得到。例如在CNN中，卷积层的滤波器（可以看作是特征提取器）初始时被随机初始化，在训练过程中，通过反向传播算法和优化器（如随机梯度下降SGD、Adam等）不断调整滤波器的参数，使得它们能够逐渐捕捉到不同层次、不同抽象程度的特征。以图像识别任务来说，底层的卷积核会学习到边缘、纹理等简单特征，而高层的卷积核则能学习到目标的部分乃至整体特征，如类似人脸的眼睛、鼻子等子特征组合。从边缘→纹理→部件→物体的各个层级表示，每一层提取本层级的子特征基系。在经典信号处理（LTI框架）中， 傅里叶基、小波基是解析定义的、与数据无关， 系统响应可表示为 y = Σ cₙ·φₙ(t)。在深度学习中， 特征基是数据驱动的、通过反向传播自适应生成的。 隐含表示为 h = f(W·x + b)，其中 W 本身就是学习到的基。 这相当于一个时变、非线性、数据依赖的超级LTI系统。 卷积核的权重空间会自发演化出类似螺旋的稳定性结构， 特征轨迹在训练动态中形成吸引子流形（可视为高维螺旋）， 这种自发对称性破缺正是涌现智能的核心。 无监督学习发现特征，对于无监督学习方法，如自编码器（Autoencoder）和生成对抗网络（GAN）等，它们可以从未标记的数据中学习到数据的内在结构和特征。自编码器通过将输入数据编码为低维表示，然后再解码还原输入，在这个过程中编码器学习到的表示就是数据的特征基。例如在图像的自编码器中，模型可以自动学习到图像的颜色分布、形状等关键特征，而不需要人为预先定义这些特征。数据驱动机器学习，AI学到的特征完全依赖于你喂给它的数据和你要解决的任务。用猫狗图片训练，它就学会区分猫狗的特征；用医学影像训练，它就学会识别病变组织的特征。机器通过数据驱动的梯度下降优化载体权重，最终形成适配任务的特征基。

当前先进的深度学习的特征自动生成能力，不但源于其多层神经网络的结构，还集成了端到端的学习方式。深度学习多层特征提取，深度学习模型（如卷积神经网络CNN、循环神经网络RNN、Transformer）通常由多个隐藏层组成，每一层都对输入数据进行非线性变换，逐层提取更复杂的特征。例如，CNN的第一层可能学习到图像的边缘、纹理等低级特征，第二层将这些边缘组合成更复杂的形状（类似眼睛、鼻子这样的中间局部子特征），更高层则将形状组合成完整的目标（如人脸、汽车）。这种“从低到高”的特征抽象过程，完全由模型自动完成，无需人工设计，自动特征生成消除了对领域专家的强烈依赖，降低了特征工程的误差和时间。例如，在人脸识别任务中，无需人工设计人脸的特征（如眼睛间距、鼻梁高度），模型能够自动从大量人脸图像中学习到这些特征，这使得深度学习能够摆脱传统机器学习的特征工程瓶颈，适应复杂数据，提升模型性能，成为当前人工智能领域的核心技术。深度学习 端到端学习，进一步将特征提取与分类/预测任务整合在一个端到端的框架中。模型直接从原始数据输入，通过反向传播算法调整权重，同时优化特征提取和任务性能。这种方式避免了传统机器学习中“特征提取与模型训练分离”的弊端，确保特征能够更好地适应任务需求。端到端学习模型通过同一网络的梯度传播进行训练，对特征基与分类器（子特征结构）联合调优。端到端学习从原始数据到最终答案，中间所有特征变换的参数都是通过反向传播算法，根据任务目标自动优化得到的。

比如，CNN的特征基是静态空间特征基，训练完成后权重固定，对任何输入，同一卷积核的表征规则不变。CNN的特征基直接对应卷积核（Kernel/Filter），不同卷积核的权重分布，就是对输入（图像/序列）不同空间特征（边缘、纹理、形状、语义）的表征基，其学习过程是卷积核权重从随机到适配数据特征的迭代优化，全程无人工定义特征规则，仅定超参数。人工仅仅指定卷积核的数量、尺寸、通道数（如3×3大小、64个核、输入通道3），这是特征基的“容器规格”，而非特征基的核心（权重）；对卷积核的权重矩阵做随机初始化特征基（如Xavier/He初始化），此时卷积核无任何特征表征能力，只是随机的数值矩阵；特征基与输入的“匹配响应” 前向传播，卷积核对输入做互相关运算，本质是用当前的随机特征基（卷积核）去匹配输入中的空间模式，输出的特征图就是输入在该特征基下的响应值（响应越高，说明输入包含该特征基对应的模式，如图像的水平边缘）；优化特征基的权重的 反向传播，根据任务损失函数（如分类的交叉熵），通过梯度下降计算卷积核权重的梯度，沿损失减小的方向更新权重——让能匹配数据真实特征（如真实图像的边缘、纹理）的卷积核响应更强，无关的响应更弱；特征基的层级演化，浅层卷积核会先学习到基础低维特征基（如图像的水平/垂直边缘、灰度突变、简单纹理），深层卷积核会将浅层特征基组合，学习到复杂高维特征基（如形状、物体部件、完整目标），最终形成一套适配任务的空间特征基体系。深度学习能够自动处理高维、非线性、非结构化的数据（如图像、语音、文本），提取出人工难以设计的有效特征。例如，CNN在图像分类任务中，能够学习到图像的深层语义特征（如物体的形状、纹理），远远超过传统手工特征（如HOG、SIFT）的性能。

比如，Transformer的是动态语义特征基，词嵌入矩阵+注意力权重 = 隐式的动态语义特征基，训练完成后，词嵌入和Q/K/V权重固定，但对不同上下文的同一token，会组合出不同的特征基，这是为NLP的上下文依赖性设计的核心逻辑。Transformer无显式的“卷积核”类特征基载体，其特征基是词嵌入层的基础特征基 + 自注意力层的动态组合特征基共同构成的语义特征基，适配NLP的上下文依赖特性，核心是让特征基随输入的上下文动态调整，学习过程比CNN更复杂，分为基础特征基初始化+动态特征基迭代优化。基础层词嵌入矩阵 = 静态的token基础特征基。 人为设定超参数，仅指定词嵌入维度（如BERT-base的768维），即特征基的维度，不定表征规则；词嵌入矩阵随机初始化，每行对应一个token的基础特征向量，此时向量无任何语义信息，只是随机的高维数值；初步映射将输入的token（如分词后的字/词）通过词嵌入矩阵，映射到低维稠密空间，形成token的基础特征基，完成从离散token到连续特征的转换。核心层自注意力（Q/K/V权重） = 动态的语义组合特征基，自注意力是Transformer特征基的核心优化模块，通过计算token间的关联度，动态组合基础特征基，生成适配上下文的语义特征基，这是和CNN静态特征基的本质区别。自注意力 权重初始化，其查询（Q）、键（K）、值（V）权重矩阵随机初始化，人为仅定其维度（与词嵌入维度一致）；前向传播先通过Q/K/V权重矩阵，将token的基础特征基映射为查询向量、键向量、值向量；计算token间的注意力得分（即语义关联度），归一化后得到注意力权重；用注意力权重对所有token的值向量做加权求和，本质是根据上下文，动态筛选、组合基础特征基，生成当前token的上下文相关语义特征基（如多义词“银行”，在“河边银行”和“金融银行”中，注意力权重会组合出完全不同的特征基）；反向传播根据任务损失，同时更新词嵌入矩阵和Q/K/V权重矩阵——让基础特征基更贴合token的固有语义，让注意力权重更精准地捕捉上下文关联，最终形成一套能动态适配不同语境的语义特征基体系。

三、“非显性子特征”识别能力的鸿沟

在传统机器学习中，特征工程（Feature Engineering）是模型性能的关键瓶颈。需要依赖领域专家的知识，通过人工设计、选择和提取子特征（如图像的SIFT特征、文本的TF-IDF特征），再将特征输入模型训练。这种方式不仅费时费力，而且子特征的优劣直接决定了模型的性能，难以适应复杂数据（如图像、语音）的高维、非线性特性。子特征分级分类提取对于人类来说非常困难，子特征的质量完全依赖于人的先验知识和甚至灵光一现，很多时候这种机遇犹如瞎猫碰死耗子，是整个系统设计的瓶颈。深度学习神经网络好似一个拥有多层自适应滤网的智能工厂，在全局约束下每一层自发筛选恰如其分的子特征属性精度粒子（如若第一层筛大颗粒，第二层筛特定形状，第三层筛特定颜色）。深度学习的特征基是机器在训练过程中自动动态生成的，而非训练前人为预先定义的。这一特性使得深度学习能够摆脱传统机器学习的特征工程瓶颈，适应复杂数据，提升模型性能，成为当前人工智能领域的核心技术。人类与深度学习AI之间，二者对于中间层“非显性子特征”的精准判定能力有着不可逾越的巨大鸿沟，所以马斯克说碳基文明只是硅基文明初始阶段的引导程序。

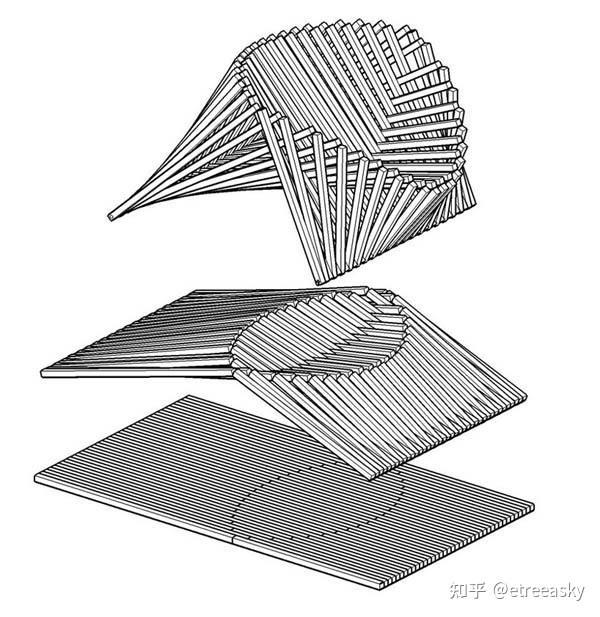
①物品空间折叠，存在“非显性”有迹可寻的折叠痕迹，AI凭借“非显性子特征”可以复原为高阶空间的显性结构。下面是斯坦福机器学习教学视频，从平面图形中还原3D、四维（3D+时间）的图像（可以从52分钟看起）：http://open.163.com/movie/2008

②卷积神经网络图像识别的各隐层权重参数集，其实根本找不到眼耳口鼻等显性子特征、也找不到各年龄性别人种脸谱的显性特征，深度学习各隐层的特征基是“非显性子特征”，这些各种层级的非显性子特征基是机器自己找到并设置的。因为其非显性特征属性脱离我们惯常认知，对人类而言宛若“黑箱”。

③围棋伙伴们以前都必须学习千百年来人类围棋大师总结的棋谱定式，但如今却都纷纷转而拜师AlphaGo学习“狗招式”，因为AI招式更有优势更胜一筹。尽管AlphaGo所有复盘参数都有，但是我们人类无法获得它的隐层策略的“非显性子特征”，也就无力获知AlphaGo的显式逻辑轨迹，人类棋手终究只好生搬硬套的引用“狗招式”，毕竟能赢人类对手就行啦。

④一位名牌大学令人羡慕医学博士，如果运气爆棚，穷极一生可能有幸揭开几个蛋白质结构；如果还得到祖坟冒清烟庇护，他有望揭开好几十个蛋白质结构从而历史留名。不过，AlphaFold(这是AlphaGo的升级版)却一下子高准确度预测了世间几乎全部所有的两亿多个蛋白质结构，这源于AlphaFold对蛋白质结构的隐藏层级的“非显性子特征”的精准判断力。两亿多个蛋白质“非显性子特征”结构谜题，曾经让知其然不知其所以然的人类工程师们惊掉下巴。

⑤爱因斯坦与波尔当年的爱波之争的焦点，在于不确定性关系△x△p=h/2 中的x和p并非粒子的实体位置{x}和动量{p}，而是粒子的位置算符和动量算符的本征值。也就是说，表面上爱因斯坦和波尔虽然都在谈位置变量x，但是他们谈的并不是同一回事。爱因斯坦指的是实数向量空间“显性的”实体特征值位置坐标{x}，而波尔说的是复数张量空间“非显性的”位置本征态的特征值x 。请注意，粒子实际坐标{x}和位置算符本征值x有本质区别。经典物理能看到的实体特征值是对角矩阵元素，经典物理触碰不到的非显性的纠缠态特征值不在矩阵对角线上。不过，深度学习的多隐层“非显性子特征”能够表达不在矩阵对角线上的位置本征态特征值x，深度学习隐层的本质功能就是提取 “非显性特征”。

• 经典物理实体空间的一个可观测物理量{x} 对应一个厄米算符。在其本征态下进行测量，结果确定性地得到相应的本征值（实数）。在该状态下，此算符的矩阵表示在其自身的本征基下是对角的，对角元就是本征值。本征值是算符固有的、实体出现的测量结果（实数）数值。

• 在量子力学中，一般的量子态（波函数）通常是多个本征态的叠加态。量子态的物理量算符特征值x的矩阵表示不一定是对角的，它是量子力学概率波期望值，即大量相同制备态下测量结果的平均值，它等于 <ψ|Â|ψ>，这可以看作是一个矩阵元（态矢量与算符作用后的内积），而不一定是对角元。