17.6 从δ函数到LTI再到智能涌现

机器人的核心在于硅基芯片，硅基芯片的基本结构是晶体管，晶体管只有0和1两种信号，本源只是两种信号的极致简单系统，凭什么诞生智能？

人脑的核心在于神经网络，神经网络的基本结构是神经元细胞，神经元细胞只有0和1两种信号，本源只是两种信号的极简系统，凭什么诞生智能？

请先看看关于智能的简单例子：黏菌群的群体具有某种智能，它们能够找出迷宫、能够规划东京地铁最优路线。 一个黏菌是没有智能的，两个三个四个五个黏菌也没有智能。但是千万个黏菌链接，却诞生了神奇的智能行为。实验测试告诉我们，这肯定跟黏菌群体的共同脉冲作用有关。

进一步看，同样的脉冲响应，形成了人脑电图。科学家在人脑神经网络研究中，神经元脉冲响应几乎是人脑作用的唯一的工具。 一个单神经元生物是没有智能的，两个三个四个五个神经元也没有智能。一亿个十亿个百亿个神经元链接，却诞生了人脑智能。OpenAI在chatGPT3.5之前默默无闻，因为GPT-1参数量只有1.17亿、GPT-2参数量只有15亿，而GPT-3.5参数量级实现跃升达到1750亿、GPT-4参数量更有1.8万亿，从平平无奇到无所不知唯一区别是参数多少，参数暴涨涌现智能，这是神经网络的真正神奇之处。

但是，为什么呢？

一、脉冲函数

脑神经元电脉冲与脉冲函数的联系是生物信息传输的数学基础。脑神经元电脉冲与脉冲函数的联系本质上是生物神经计算与数学信号处理的对应关系，神经元通过脉冲序列编码信息，其动态行为可用LTI系统的冲激响应和卷积积分精确描述。这种数学框架不仅解释了神经信息处理的基本原理，还为设计高效的脉冲神经网络提供了理论基础。脉冲函数抽象了神经元电脉冲的核心信号特性，让神经生理的定量分析成为可能。

生物神经元的电脉冲具有“全或无”特性，当膜电位总和达到阈值时，会产生固定幅度、持续1-2ms的动作电位，电位本身的形状不携带信息，仅通过发放时刻和频率传递信号，这和数学中脉冲函数（仅关注发生时刻、忽略具体形态的瞬时信号）的核心特征高度契合。神经元的膜电位动态特性与RC电路的电压动态特性高度相似，可被类比为带有电阻和电容的低通滤波电路，其中电容特性对应膜的积分过程，离子通道对应电阻的泄漏过程。脑神经元的电脉冲（动作电位）是神经信息传输的核心载体，而脉冲函数（尤其是狄拉克δ函数）是其数学建模的关键工具，二者的联系贯穿于神经科学理论与计算模型之中。这些特性完美匹配神经元电脉冲的瞬时放电特征，神经元在接受输入信号后，膜电位会快速上升至阈值并产生一个短暂的脉冲（动作电位），随后迅速恢复至静息状态。将神经元简化为“累积输入-阈值触发脉冲”的过程，把动作电位抽象为一个瞬时脉冲事件，完全复刻了脉冲函数的核心属性；麦卡洛克-皮特斯（MP）模型则通过阶跃函数模拟神经元的激活逻辑，进一步用数学方式将神经元电脉冲的“触发/不触发”状态与脉冲函数的“存在/不存在”对应起来，为人工神经网络的信号处理逻辑奠定了基础。核心是神经元动作电位的“全或无”尖峰特性、事件化编码本质，与脉冲函数（狄拉克δ/单位冲激）的数学抽象高度契合，脉冲函数是神经元电脉冲在理论建模中的核心数学工具，也是连接神经生理现象与定量分析的桥梁。神经元动作电位是幅值固定、时宽极窄的尖峰脉冲（全或无，无中间幅值），理想狄拉克δ函数是时宽为0、积分归一的脉冲抽象，实际建模中会用窄脉冲近似δ，精准捕捉神经元电脉冲的事件性（信息编码仅关注发放时刻/频率，而非幅值细节）。神经元电脉冲（动作电位）是神经信息传递的基本单位，其数学本质可被精确描述为脉冲函数。在脉冲神经网络(SNN)中，神经元通过离散的脉冲序列而非连续值进行通信。动作电位的产生遵循"全或无"原则：当膜电位达到阈值时，神经元会瞬间发放一个固定幅度的脉冲（约100mV），随后膜电位重置，这一过程可被数学建模为狄拉克δ函数。

在信号处理中它往往被称为脉冲函数（量子力学一般称为狄拉克δ冲激函数）， 它的数学定义为：

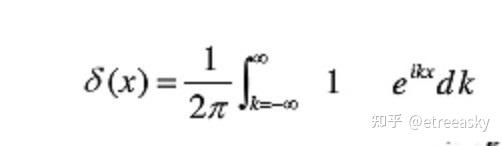
同时，冲激函数δ的傅立叶变换是“单位1 ”（ℵ2维度态空间的“单位1 ”等价于ℵ1）：

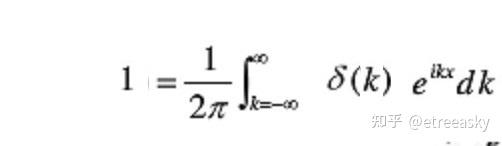
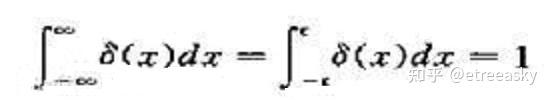
然而，如此重要的冲激函数δ在我们数学系看来屁都不是，既不能叫“数”，更不能称为“函数”。它异常怪异的数学等价式子为：

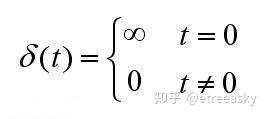
从δ冲激函数的定义可以看出它非常特别、另类、异形。非数学专业的同学一般看不懂，数学专业的同学更加看不懂。

因为这个怪胎函数仅在0点一个点有值、这个点值是∞、其积分等于1（积分宽度为0、高度为∞、面积是1）。翻译成白话文大家就明白了，口水话的解释相当于：

‘什么都没得’ × ‘无穷大’ ＝ ‘有东西’

数学表达为： 0 × ∞ ＝ 1

零乘以无穷大等于1，对于数学系以外的人而言并无不妥，但放在严谨、严格、严肃的数学体系中，它就是扎眼的鬼精灵，令人不安恐惧。 因为在数学系统中，0 和 1 是确定的数值，而 ∞ 根本不是什么数值。还记得上小学时老师反复告诉过我们1/0是无意义的么，为什么0不能作为分母，估计小学老师也说不出所以然。其实， 1/0为什么无意义，是因为 1/0 如果有意义将等于∞，而如果1/0＝ ∞ ，那么意味着两个“确定的”数的算术运算将等于“不确定”，这在数学逻辑中完全无法解释 。 两个确定数值运算怎么能和∞这种非数值符号相等呢？

冲激函数的冲击波异常强劲，一方面它让数学界异常窘迫尴尬，数学根本解释不同这是个什么东西；一方面冲激函数的应用取得了巨大成功，甚至可以说如果没有冲激函数就没有量子力学、信号学、傅立叶变换。 最初，哥本哈根学派发现了冲激函数可以解决大量实际问题，不管三七二十一，拿来就用了，很好用，慢慢大家发现这个鬼东西是个好东西，你也用他也用，泛滥开来。在这个过程中数学家参与进来 ，试图按数学一贯的方式对这个函数进行规范化标准化定义，这时数学家才发现δ这个鬼东西根本无法招安，气的发抖（想当年，我们数学系的希腊先祖们为了√2的‘无理’甚至可以杀同伴，思维局限害死人啊）。

虽然δ函数不易驯服，但它本事相当大。

神经元的单个电脉冲可理想化地用δ函数表示，若神经元在时刻t_i放电，则其电脉冲信号可写为s(t) = \ ∑_i \δ(t-t_i)，其中t_i是第i个脉冲的发放时间。傅里叶变换将脉冲序列转换为频率域，分析其功率谱（Power Spectrum），从而了解神经元对不同频率刺激的敏感性（如视觉神经元对高频光的响应）。神经元在自然环境中的放电并非完全规则的，其脉冲序列往往具有随机性（如视觉皮层神经元对自然图像的响应）。为了计算分析这种随机脉冲序列，通常采用泊松过程（Poisson Process）模型，δ函数是构建该模型的基础，通过积分或求和操作描述脉冲序列的时间分布，从而量化神经元的放电特性（如发放率、 interspike interval 分布）。

神经元间的信号传递可简化为前神经元脉冲输入→突触的冲激响应，即突触后电位的生成是输入脉冲序列与突触冲激响应的卷积，这是脉冲神经网络（SNN）、神经动力学建模的底层框架，而脉冲函数是卷积运算的核心元，通过计算输入信号与δ函数的卷积，卷积分析可提取神经元对特定刺激的响应。多个神经元的脉冲输入在突触后神经元的空间/时间总和，可通过脉冲函数的线性叠加定量描述，匹配生物突触后电位的整合规律；即使考虑神经元的不应期、非线性，脉冲函数仍是基础建模单元。

更加令数学大师们不安的是，δ函数是信息光学的基元函数、是傅立叶变化的取样基底，但遗憾的是Hilbert空间对δ函数等广义函数的内积无定义，Hilbert空间无法以普通函数表达δ函数以及延时δ函数的正交性。前面探讨过，究其根本这是单层向量空间（Hilbert连续普空间）的局限性，而δ基元函数和exp(ipr)复指数基元函数一样都是高阶张量系统的基底，也就是说δ基元函数支持“深度学习”的多层次逻辑模型，支持对多重线性映射系统的度量。

时域的时延相当于频域的相位，δ函数在线性时不变系统中体现卷积特性：

二、复杂系统的整体单一特征

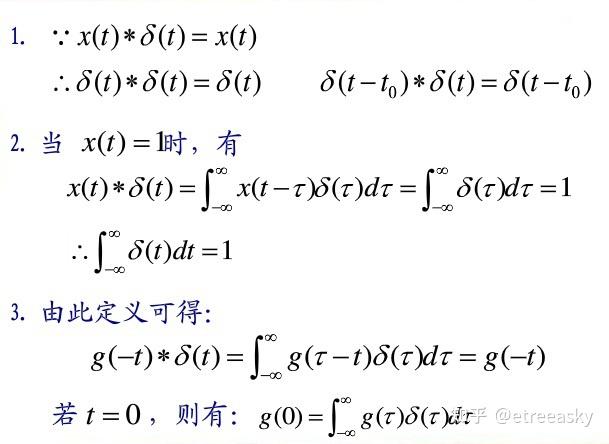
奇怪如果输出只是完全相同的脉冲，信息如何传递呢？

为什么有的复杂的系统在整体上的呈现单一特征性，我们可以从冲激响应h的性质一窥究竟。如果输入为冲激函数δ，经过某系统（最好是线性时不变系统），则输出为冲激响应h。冲激响应h 是高维度转化为一维的关键。

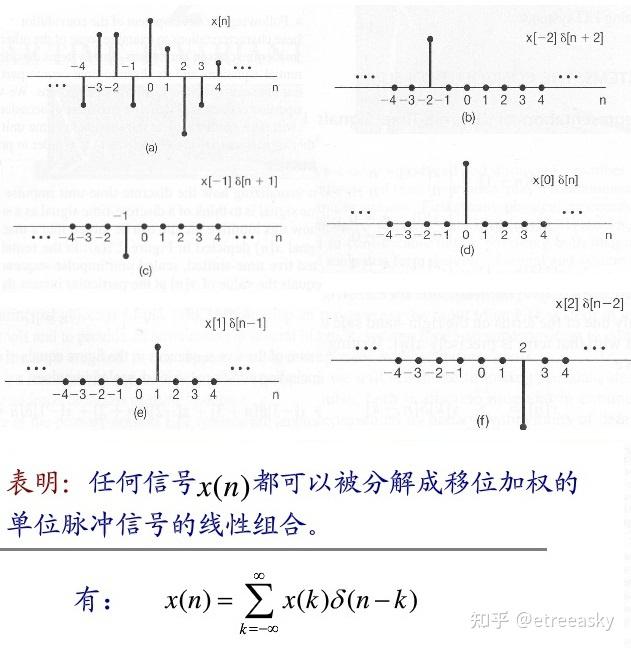
首先，由于冲激函数δ是普遍意义的基元函数，所以信号总能以δ为基底进行分解：

第二，更重要的是，因为线性和时不变性两项性质，冲激响应h 为基底的输出，实际上是一个卷积：

上面这个式子，即：

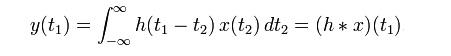
请注意，这是只有一个自变量t1的一维函数！

复杂的连续无穷维的微分积（积分），可以变成能够简单直乘的卷积运算。通过卷积定理，复杂的连续无穷维子要素重叠叠加，变成了一维整体逻辑轨迹。基于此，即使环境要素纷繁复杂，复杂系统有可能瞬间涌现智能直觉。

由于线性时移不变性，一个复杂图形在n维空间中会保持“不变形的移动”，在场论中这体现为单一轨迹运动。

三、以LTI系统为基础的智能涌现

大脑神经元细胞遵循“全或无”定律——要么完全产生、要么完全不产生，信号没有中间状态，只存在“通过”和“不通过”两种信号，要么处于活跃状态触发、要么处于抑制状态不触发，单个神经元的输出是数字“1”脉冲或“0”信息，这是一个强度、形状固定的电脉冲。机器学习中，算法通过给晶体管网络的连接分配连续值权重，让简单的0/1电信号在层级传递中完成“原始数据→浅层特征→深层语义”的转化，再通过海量数据训练不断优化权重，最终涌现出识别、推理、决策等智能行为，最终结合AI算法形成层级化的特征提取与模式推理体系。其智能是工程化的复杂连接+数据驱动的模式拟合的结果，0/1只是传递信息的物理基础。

人脑约有860亿神经元，每个神经元有1000-10000个突触连接，形成14-15个数量级的突触总量，每秒可进行约40万亿次大规模并行计算处理能力。 现代AI模型如GPT-4拥有数万亿参数，通过并行计算实现复杂任务处理，远超单个晶体管或神经元的能力。“硅基芯片（晶体管0/1信号）”与“人脑（神经元0/1脉冲）”为何能诞生智能的问题，核心逻辑在于简单单元的规模化组织与相互作用——无论是晶体管的二进制开关，还是神经元的脉冲信号，其智能都不是来自单个单元的“0/1”本身，而是大量单元通过特定结构（如神经网络）连接后，涌现出的复杂信息处理能力。

在神经网络中，信息通过多层级化特征提取，底层提取简单特征（如图像中的边缘），中层组合成复杂结构（如眼睛、轮子），高层形成抽象概念（如人脸、汽车），多层堆叠非线性复合 → 万能逼近，非线性层级将单元运算从"多维加法" 升级到“高阶复合"变换。 这种非线性叠加与多层抽象使系统能够从简单输入构建复杂表示是智能涌现的核心机制。例如，当神经网络学习识别猫的图片时，它不是记住所有猫的图像，而是学习从像素到边缘、到纹理、再到整体形状的层级化特征表示。智能的真正来源在于系统层级的复杂性，而非基础单元的简单状态。 高级认知功能（感知、决策、创造力）并非来自单个神经元的“0/1”，而是860亿个神经元通过复杂网络连接后，大规模互联形成高维特征状态空间，涌现出的全局功能——正如神经网络中的“涌现性”（Emergence），当网络规模达到一定程度时，会突然出现新的功能（如图像识别、自然语言处理），而这些功能无法通过单个神经元的特性预测。这种简单单元的规模化涌现，是智能的本质——无论是硅基还是碳基，只要满足足够的单元数量、合理的连接结构、有效的学习机制，就能诞生智能。而硅基芯片与人脑的差异，主要在于单元类型（晶体管 vs 神经元）、连接方式（逻辑门 vs 突触）、学习机制（算法 vs 经验），但智能的本质是一致的。

整个神经系统的信息编码是高度复杂的模拟-数字混合系统，其信息蕴含在脉冲群体的时间复合模式中。关键在于 “脉冲频率编码” 和更精细的 “时间编码”：频率编码是最主要的方式，刺激强度越强，神经元在单位时间内产生的动作电位脉冲串的频率就越高。例如，轻触皮肤可能引发每秒10次的放电，而重压可能引发每秒100次的放电。时间编码通过精确的脉冲时序、脉冲间的间隔模式、与其他神经元脉冲的同步性等，都承载着丰富信息。例如听觉神经元会对特定声音频率产生相位锁定的放电。脉冲频率编码w、时间编码t、复数i是exp(ipr)中的三个元素，由于“原空间平移基矢⊗对偶空间旋转基矢”的高阶复合空间参照系具有完备性，而复空间与张量空间等价。exp(ipr)是全体线性时不变系统的公共基，并且它是傅里叶变换的本征函数、它也是冲击函数δ的本征函数，所以它是卷积变换的所有系统的共同本征基，这使得它在深度学习多隐层张量结构中具有广泛深远意义。

信号本身无智能，但当它们在连续时间中流动并改变连接权重（特征值）， 权重矩阵f{w}的不动点形成吸引子（螺旋结构）记忆功能，学习信号相关性雕刻状态空间地形特征，系统轨迹在高维流形上的演化逻辑能力。智能涌现的基础在于 ① 巨大的规模：天文数字的单元数量，提供了表达复杂性的物理基础。② 复杂的连接：单元之间形成非平凡的拓扑结构，允许信息以复杂的方式传递和整合。③ 非线性的相互作用：每个单元或连接都进行非线性变换（如神经元的阈值特性、激活函数），使得整体行为远非各部分之和。④ 层次化的组织：低层提取特征，中层整合信息，高层进行抽象和决策，这种层级处理是理解复杂世界的关键。⑤ 可塑性/可编程性：系统能够根据经验（数据）改变自身状态（参数/连接权重），从而适应环境、学习和记忆。

终极答案框架：0/1信号（离散事件层）脉冲函数δ(t-tk)激励， 通过LTI膜动力学（连续时间层）， 经非线性σ(·)调制螺旋吸引子（涌现智能层）

智能与LTI系统的联系是动态系统智能化的核心框架。LTI系统将复杂的生物/智能现象进行数学分析的关键工具，提供了智能信息处理的基础运算框架，让智能的建模、设计和实现成为可能。智能（尤其是计算智能）的核心是对动态系统的建模与控制，而线性时不变（Linear Time-Invariant, LTI）系统是其基础框架。LTI系统的特性（线性性、时不变性）与智能算法的设计（如自适应控制、机器学习）密切相关。智能的本质是对环境的适应与调控，而LTI系统的线性性与时不变性为其提供了可预测性与可控性， 可预测性方面是LTI系统的输出仅依赖于当前输入与历史状态（马尔可夫性），因此其未来行为可通过当前状态与输入预测。这种可预测性是智能系统（如机器人、自动驾驶）的基础，使其能提前规划行动； 可控性方面是LTI系统的能控性与能观性是智能控制的核心概念。能控性指系统可通过输入控制到达任意状态，能观性指系统可通过输出来推断内部状态。智能系统（如自适应控制器）通过设计输入，使系统保持能控与能观，从而实现稳定控制；LTI系统的最优控制，如线性二次 regulator, LQR）通过最小化性能指标（如能量消耗、跟踪误差），实现对系统的最优调控。这种优化思想是智能系统（如机器人路径规划、资源分配）的核心，使其能在约束条件下实现最优性能。

机器学习的核心是从数据中学习模型，LTI系统是许多机器学习算法的隐式框架。比如，循环神经网络RNN通过循环连接处理时序数据，其状态更新方程x_{k+1} = f(x_k, u_k)（x_k为状态，u_k为输入）是LTI系统的离散形式（若f是线性函数）。例如，长短期记忆网络（LSTM）的门控机制（输入门、遗忘门、输出门）本质上是LTI系统的非线性扩展，用于控制信息的流动； 卷积神经网络CNN的卷积层是LTI系统的空间域扩展。卷积核（Kernel）h(i,j)相当于LTI系统的冲激响应，通过卷积操作提取输入图像的特征（如边缘、纹理），其输出y(i,j) = \ ∑_{m,n} x(i+m,j+n) h(m,n)是输入与卷积核的线性组合； 强化学习的核心是马尔可夫决策过程，其状态转移概率p(s'|s,a)（s为当前状态，a为动作，s'为下一状态）是LTI系统的概率扩展。例如，Q-learning算法通过估计状态-动作值函数Q(s,a)，实现对MDP的最优控制，其本质是对LTI系统的动态规划。

智能控制的关键是对动态系统的调控，LTI系统是多数智能控制算法的基础模型。实际的脑功能和真正的智能，本质是这些基础数学工具在非线性、时变、动态、群体协同下的高阶涌现结果。LTI系统是智能信息处理的“底层基础框架”，智能的感知、表征、基础信息加工等核心环节依赖LTI的卷积、滤波、傅里叶分析等核心运算，而智能的高阶特性（学习、决策、泛化）则源于LTI模块的组合与非线性拓展，LTI是智能从“现象”到“定量建模/工程实现”的关键基石。智能的起点是环境信号（图像、声音、触觉）感知，这类物理信号的预处理、初级特征提取均以LTI运算为核心——如图像边缘检测（卷积滤波）、声音频谱分析（傅里叶变换，LTI的频域核心特性），生物视觉/听觉初级皮层的处理（如感受野）也被大量建模为LTI滤波网络。LTI的叠加性、时不变性让信息处理过程可严格数学分析、预测和设计，是智能系统从“经验试错”到“理论构建”的前提；即使是深度学习，其卷积层（空间局部化LTI）、全连接层（全局线性变换，LTI特例）也是底层核心模块。

虽然纯LTI系统不具备真正的智能（无自主学习、非线性决策、泛化能力），但是智能的非线性核心（如生物脑的突触可塑性、机器学习的激活函数/决策层）均以LTI模块为基础构建——如CNN的“卷积层（LTI）+激活函数（非线性）”、生物大脑的“初级LTI-like处理→高级皮层非线性整合”的层级结构，都是LTI拓展为智能的典型形式。LTI系统可作为某些低级信息处理的近似工具基础，但无法刻画智能的核心特征，智能必须用非线性、自适应、高阶系统来描述。对复杂智能行为的初步建模，常先通过LTI捕捉核心规律，再引入时变、非线性、反馈等特性逼近实际；从LTI到线性时变（LTV）、仿射系统，再到非线性系统的拓展，正是生物智能和机器智能建模的核心研究方向。智能系统与线性时不变系统(LTI)的关系则揭示了神经计算的本质机制。线性时不变系统(LTI) 为理解神经计算提供了关键的数学框架。脉冲神经元系统是LTI系统的特例，单个神经元可被视为一个线性时不变滤波器，其输入是突触前脉冲序列，输出是膜电位动态，而脉冲发放则是对膜电位超过阈值的非线性响应。突触后电位ϵ_{ij}(t)本质上是系统对脉冲输入的冲激响应，描述了神经元对单个脉冲的线性响应特性。突触后膜电位可表示为输入脉冲序列与突触响应的卷积：u_i(t)= ∑_{j} ∑_{f} ϵ{ij} (t-t{j}^{(f)}) +u_ rest，这正是LTI系统输入-输出关系的标准数学表示。脉冲神经网络(SNN) 可被视为由多个LTI系统组成的复杂网络。每个突触可被视为一个IIR滤波器，其输入是脉冲序列，输出是突触电流，而神经元整体则是一个滤波器网络。神经元的动态行为可用状态空间方程描述，其中膜电位和突触电流作为状态变量，输入是突触前脉冲，输出是突触后脉冲。神经元的膜电位动态是线性过程（积分和泄漏），而脉冲发放是非线性过程（阈值触发），这种结构使SNN能够同时处理线性和非线性信息。大脑的智能计算可被视为多层LTI系统的级联，每一层处理特定频率范围的信息，类似于信号处理中的滤波器组。通过突触可塑性（如STDP学习规则），神经网络能够动态调整其LTI特性，实现对环境的适应和学习。SNN的事件驱动特性（仅在脉冲发放时计算）使其比传统ANN更节能，这与LTI系统仅在输入变化时响应的特性一致。

神经元电脉冲通过脉冲函数连接了离散事件与连续LTI系统；智能则通过"大规模非线性网络"在LTI的基底上涌现。智能系统 = 脉冲驱动的非线性振荡器网络 × 多尺度螺旋动力学，智能作为"调制的LTI螺旋"，智能行为可拆解为LTI子系统 + 切换控制器，任何非线性动态都可局部线性化为LTI（雅可比矩阵本征分析），脑波的α、β、γ频段分析本质是时空LTI滤波， 体现为傅里叶对偶的频域智慧，非线性耦合 → 螺旋吸引子（记忆、预测）。

智能与LTI系统的联系揭示了智能计算的本质机制。大脑的智能源于大量简单LTI单元（神经元）通过复杂连接形成的网络，这些单元通过线性积分和非线性阈值触发的组合，实现了对复杂环境的适应和学习。这一视角不仅深化了我们对生物智能的理解，还为开发更高效、更节能的人工智能系统提供了新思路。这种深刻联系表明，理解神经计算的数学本质（特别是LTI系统特性）对于开发新一代人工智能技术至关重要，也为脑机接口、神经疾病诊断和神经形态计算等领域提供了关键的理论支撑。

黑客帝国虚拟空间曾经颠覆了多少人三观，回过神来那不过只是绚丽的虚构。但是当前，现实版黑客帝国前传已经来临：Neuralink脑机猕猴意念玩游戏

转载本文请联系原作者获取授权，同时请注明本文来自陈正茂科学网博客。
链接地址：https://wap.sciencenet.cn/blog-1666470-1521866.html

上一篇：深度学习多隐层架构数理逻辑浅析（十七）（5）